Vorlesung 6 Thomas
Aus ProgrammingWiki
Inhaltsverzeichnis |
Aufgabe 1
Defnieren Sie je eine totale Funktion für den Vorgänger und die Halbierung einer natürlichen Zahl. Defnieren Sie außerdem eine Funktion mit $ D_f = \N \setminus \{1234, 7266281\} $.
Funktionsdefinition Vorgänger (total) :
$f(n) =
\left \{
\begin{array}{ll}
n-1 & \mbox{, wenn n} > 0\\
0 & \mbox{, sonst.} \\
\end{array}
\right.$
Halbierungsfunktion: $g(n) = \left \{ \begin{array}{ll} \frac{ n }{ 2} & \mbox{, wenn n gerade } \\ \frac{ n+1 }{2} & \mbox{, sonst.} \\ \end{array} \right.$
Funktion mit $D_f = \N \backslash \{1234, 7266281\}$: $h(n) = \left \{ \begin{array}{ll} n & \mbox{, wenn }n \neq 1234 \mbox{ und } n \neq 7266281\\ 1 & \mbox{, sonst.} \\ \end{array} \right.$
Aufgabe 2
Was liefert eigentlich haelt?(haelt?) bzw. $(haelt? haelt?)$?
$haelt?(f) = \left \{ \begin{array}{ll} wahr & \mbox{, wenn haelt_fuer_n?(f , 0);}\\ falsch & \mbox{, sonst.} \\ \end{array} \right.$
$haelt?$ als Funktion ($f$) einfügen ...
$haelt?(haelt?) = \left \{ \begin{array}{ll} wahr & \mbox{, wenn haelt_fuer_n?(haelt? , 0);}\\ falsch & \mbox{, sonst.} \\ \end{array} \right.$
es folgt ein Aufruf von $haelt?(0)$ in der Funktion $haelt\_fuer\_n?(haelt? , 0)$.
Die Funktion $haelt?(f)$ erwartet eine Funktion und keine Natürliche Zahl, somit ist der Aufruf $haelt?(0)$ unzulässig. Es kommt zu einen Fehler.
Aufgabe 3
Aufgabe 4
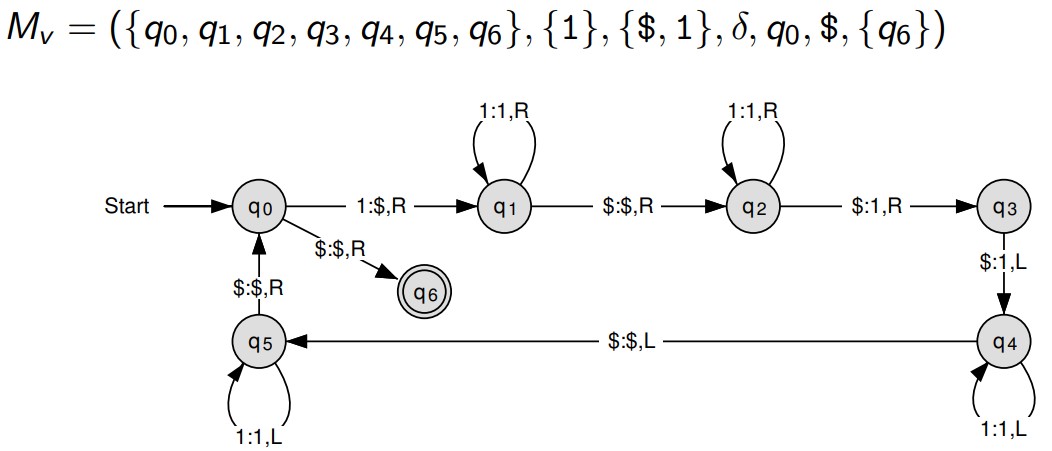
Turing-Maschine berechnet Funktion - Verdopplungsmaschine
$ 11, q0, 0 $
$ \$1, q1, 1 $
$ \$1\$, q1, 2 $
$ \$1\$\$, q2, 3 $
$ \$1\$1\$, q3, 4 $
$ \$1\$11, q4, 3 $
$ \$1\$11, q4, 3 $
$ \$1\$11, q4, 2 $
$ \$1\$11, q5, 1 $
$ \$1\$11, q5, 0 $
$ \$1\$11, q0, 1 $
$
\$\$\$11, q1, 2
$
$ \$\$\$11, q2, 3 $
$ \$\$\$11, q2, 4 $
$ \$\$\$11\$, q2, 5 $
$ \$\$\$111\$, q3, 6 $
$ \$\$\$1111, q4, 5 $
$ \$\$\$1111, q4, 4 $
$ \$\$\$1111, q4, 3 $
$ \$\$\$1111, q4, 2 $
$ \$\$\$1111, q4, 1 $
$ \$\$\$1111, q5, 1 $
$ \$\$\$1111, q0, 2 $
$ \$\$\$1111, q6, 3 $