Vorlesung 4 Lemke

Aus ProgrammingWiki

Inhaltsverzeichnis 1 Übungsaufgabe S. 11 1.1 Beispiel Ermittlung x und y aus z 2 Kreativaufgabe S. 15 2.1 Aufzählfunktion für semi-entscheidbare Menge 3 Übungsaufgabe S. 26 3.1 Beweis Wenn die Menge M entscheidbar ist, dann ist M aufzählbar 4 Übungsaufgabe S. 32 4.1 Illustration Beweis: Wenn M und A*\M aufzählbare Mengen sind, dann ist M eine entscheidbare Menge 5 Übungsaufgabe S. 33 5.1 Darstellung verschiedener Mengen in einem Venndiagramm 5.1.1 Vorabüberlegungen 5.1.2 Als Venndiagramm 5.1.3 Mit Mengenrelationssymbolen ausgedrückt

Übungsaufgabe S. 11

Beispiel Ermittlung x und y aus z

Kreativaufgabe S. 15

Aufzählfunktion für semi-entscheidbare Menge

Achtung, dieser Code funktioniert nur auf UNIX-Systemen.

import signal from itertools import product from math import sqrt ALPHABET = ['a', 'b', 'c'] a = 'abab' def timeout(signum, frame): raise Exception('Stop waiting') def semi_chi(word): if word.startswith('ab'): return True else: while True: pass def generate_words_with_length(length): return ["".join(x) for x in product(ALPHABET, repeat=length)] def generate_wordset(): length = 0 while True: for w in generate_words_with_length(length): yield w length += 1 def get_word_at(wordset, index): for i in range(index+1): w = next(wordset) if i == index: return w def get_x_y_from_z(z): w = int((sqrt(8 * z + 1) -1) / 2) t = int((w * (w + 1)) / 2) # has to be typecast bc otherwise it will be .0 float y = z - t x = w - y return (x, y) def generate_M(z): x, y = get_x_y_from_z(z) signal.signal(signal.SIGALRM, timeout) signal.alarm(y+1) try: word = get_word_at(generate_wordset(), x) if semi_chi(word): return word except Exception: return a

for z in range(20): print(generate_M(z))

ausführen

Übungsaufgabe S. 26

Beweis Wenn die Menge M entscheidbar ist, dann ist M aufzählbar

• entscheidbar: Es gibt eine totale, berechenbare charakteristische Funktion, die für jedes Wort aus der Wortmenge A* entscheidet, ob es in der Menge M ist oder nicht.
• aufzählbar: Es gibt eine totale, berechenbare surjektive Funktion, die die natürlichen Zahlen auf alle Elemente aus M abbildet

Zu zeigen: Wenn M entscheidbar, dann M aufzählbar

Wir haben also eine Menge M, von der wir wissen, dass sie berechenbar ist. Das heißt, es gibt eine charakteristische Funktion, die uns für jedes beliebige Wort aus A* ein wahr oder falsch zurückgibt, je nachdem, ob das Wort in M ist oder nicht.

Wir können nun eine Aufzählfunktion konstruieren. Diese totale, berechenbare, surjektive Funktion muss die natürlichen Zahlen auf die Elemente von M abbilden. Anders gesagt, für jede natürliche Zahl generiert sie ein dazugehöriges Element von M, wir können mit ihr die gesamte Menge generieren.

Mithilfe der vorhandenen charakteristischen Funktion können wir folgende Aufzählfunktion schreiben:

''' def generate_set(wordset, chi): for word in wordset: if chi(word) == True: yield word '''

Somit haben wir bewiesen, dass wir aus der Eigenschaft der Entscheidbarkeit ableiten können, dass eine Menge auch aufzählbar ist.

Nun ist auch zu zeigen, dass das Umgekehrte auch nicht gilt. D.h. wir können nicht schlussfolgern, dass eine beliebige Menge entscheidbar ist, wenn wir wissen, dass sie aufzählbar ist.

An dieser Stelle können wir auf den zuvor gebrachten Beweis (S. 2-13) verweisen. Hier hatten wir gezeigt, dass jede aufzählbare Menge auch semi-entscheidbar ist und jede semi-entscheidbare auch aufzählbar. Dadurch, dass hier die Semi-Entscheidbarkeit schon ausreicht, können wir nicht die Entscheidbarkeit aus der Aufzählbarkeit einer Menge folgern.

Übungsaufgabe S. 32

Illustration Beweis: Wenn M und A*\M aufzählbare Mengen sind, dann ist M eine entscheidbare Menge

def chi_from_generators(word, M_generator, not_M_generator): while True: if word == next(M_generator): return True elif word == next(not_M_generator): return False def generate_odd_numbers(): n = 1 while True: yield n n += 2 def generate_not_odd_numbers(): n = 0 while True: yield n n += 2

test_word = 4 print(chi_from_generators(test_word, generate_odd_numbers(), generate_not_odd_numbers()))

ausführen

Übungsaufgabe S. 33

Darstellung verschiedener Mengen in einem Venndiagramm

Vorabüberlegungen

• Klasse der abzählbaren Mengen ist die größte, weil sie überabzählbar unendlich groß ist. Die Potenzmenge von A* ist äquivalent dazu, weil sie alle möglichen Sprachen über A enthält, d.h. alle abzählbar unendlich großen Mengen. Es ist quasi die Klasse der abzählbaren Mengen, aber mit dem Kontext der formalen Sprachen. Außerdem ist sie auch überabzählbar unendlich groß. Die Potenzmenge von A* ist keine Menge von Mengen, sondern ein Element einer Menge von Mengen. Sie gehört zur Menge der überabzählbar großen Mengen, genau wie die Menge der abzählbaren Mengen, die auch zur Menge der überabzählbar unendlich großen Mengen gehört. Alle folgenden Mengen sind nur abzählbar unendlich groß bzw. endlich.
• Klasse der aufzählbaren Mengen = Klasse der semi-entscheidbaren Mengen (folgt aus vorherigem Beweis)
• Klasse der entscheidbaren Mengen < Klasse der semi-entscheidbaren Mengen (folgt aus Definition)
• Potenzmenge von A ist endlich, also die kleinste der Mengen, weil alle anderen unendlich sind Element der Menge der endlichen Mengen.
• A* ist die zweitkleinste Menge, weil sie nur die Wörter, die mit A gebildet werden können, enthält, während die anderen Mengen Mengen mit den Elementen von A* enthalten (nicht sicher hier) Element der Menge der abzählbaren Mengen.
• Klasse der endlichen Mengen ist die kleinste und enthält die endlichen Mengen A und die Potenzmenge von A

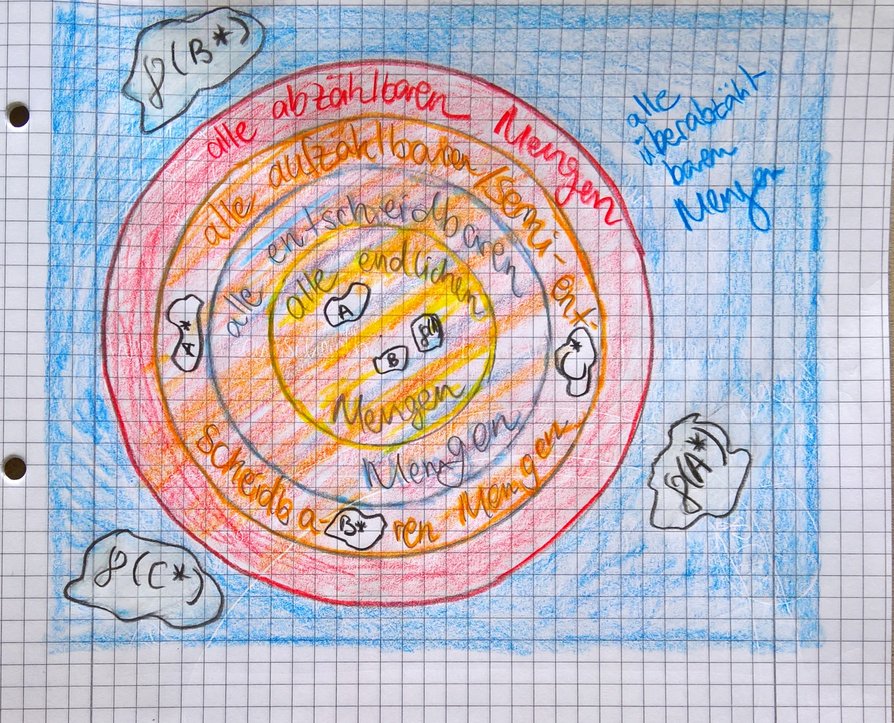
Als Venndiagramm

Erläuterungen zur Abbildung:

• Elemente von Mengen sind dadurch zu erkennen, dass sie nicht die Farbe der umgebenden Menge teilen
• Teilmengen sind dadurch zu erkennen, dass sie die Farbe der umgebenden Menge teilen

Mit Mengenrelationssymbolen ausgedrückt

• Menge(endlicheMengen) ⊂ Menge(entscheidbareMengen) ⊂ Menge(aufzählbareMengen) = Menge(semi-entscheidbareMengen) ⊂ Menge(abzählbareMengen)
• Menge(überabzählbareMengen) ist die Komplementmenge zu Menge(abzählbareMengen)
• Menge(abzählbareMengen) ∈ Menge(überabzählbareMengen)
• ℘(A*) ∈ Menge(überabzählbareMengen)
• A* ∈ Menge(aufzählbareMengen)
• A, ℘(A) ∈ Menge(endlicheMengen)