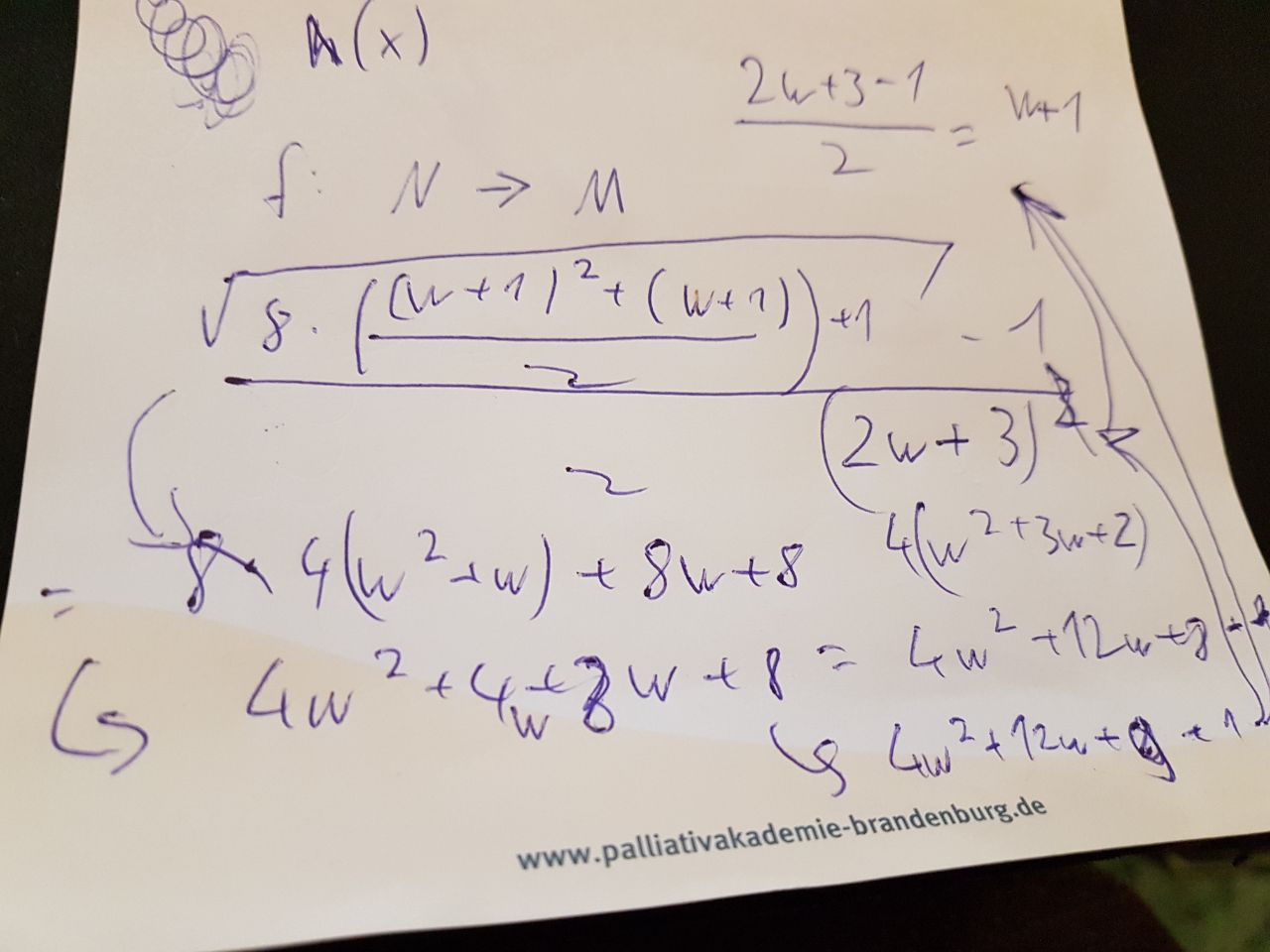Aus ProgrammingWiki

Inhaltsverzeichnis 1 Seite 10/11 2 Seite 26 3 Seite 28 4 Seite 32 5 Seite 33

Seite 10/11

$\frac{\sqrt{8 \cdot \frac{(w+1)^2 + w + 1}{2} + 1} - 1}{2}$

$\pi(1, 3) = 13 = \frac{2}{(1 + 3) (1 + 3 +1)} + y = 4 \cdot 5 / 2 + 3 = 10+3 = 13$

Seite 26

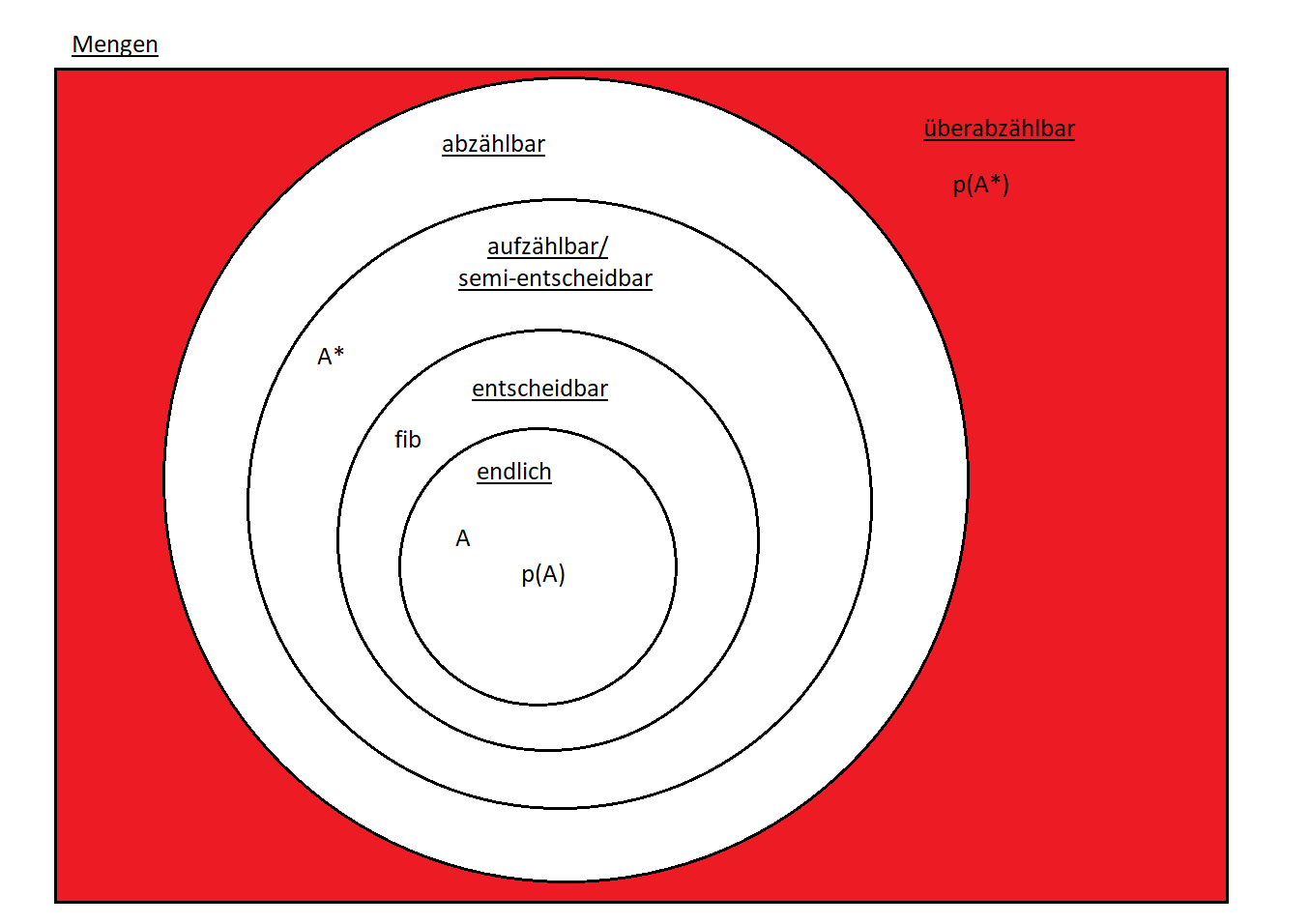
entscheidbar: $\chi$ liefert für alle Wörter ob sie in der Menge M sind oder nicht und ist berechenbar

aufzählbar: total surjektive berechenbare Funktion welche $\mathbf{N} \rightarrow M$

Wenn M entscheidbar dann M aufzählbar

Wir iterrieren durch $A^*$ g: $\mathbf{N} \rightarrow A^*$. Wir bekommen somit alle Wörter von $A^*$ und fragen die charakteristische Funktion $\chi$, ob das Wort w in $M$ ist oder nicht. Falls nicht dann bildet man $n$ auf ein Element aus $M$ (a) ab. Falls es enthalten ist, dann $n \rightarrow w$

Falsch: Wenn $M$ aufzählbar dann $M$ entscheidbar

Notbremse nicht immer vorhanden

Seite 28

entscheidbar: $\chi$ liefert für alle Wörter ob sie in der Menge M sind oder nicht und ist berechenbar

aufzählbar: total surjektive berechenbare Funktion welche $\mathbf{N} \rightarrow M$

Wenn $M$ entscheidbar, dann $M$ und $A^* \setminus M$ aufzählbar

Wir iterrieren durch $A^*$ g: $\mathbf{N} \rightarrow A^*$. Wir bekommen somit alle Wörter von $A^*$ und fragen die charakteristische Funktion $\chi$, ob das Wort w in $M$ ist oder nicht. $M$: Falls nicht dann bildet man $n$ auf ein Element aus $M$ (a) ab. Falls es enthalten ist, dann $n \rightarrow w$ $A^* \setminus M$: Falls nicht dann $n \rightarrow w$. Falls es enthalten ist, dann $n \rightarrow a$ aus $A^* \setminus M$

Seite 32

def M(n): return 2 * n + 1 def A_M(n): return 2 * n def menge_bis(M, n): print([M(i) for i in range(n)])

menge_bis(M, 10) menge_bis(A_M, 10)

ausführen

def chi_M(n): c = 0 while True: if M(c) == n: print(True) return if A_M(c) == n: print(False) return c += 1

chi_M(9199)

ausführen

Seite 33