Vorlesung 2 Thomas
Aus ProgrammingWiki
Seite7
Prinzipiell Unlösbares
Nicht formalisierbar bzw. nicht effizient:
- Unzugängliches (wenigstens) für Computer
- Fragestellungen, die sich nicht formalisieren lassen (Wann stirbt man, wird reich, …)
- Praktisch Unmögliches
- Effizienz von Algorithmen (hoher exponentiellen Aufwand)
- praktische Grenzen (Zeit und Speicher)
-> Parameter haben Einfluss auf die Lösung -> Je mehr Parameter desto besser? schneller? die Lösung…
Bsp: Stundenplan (Lehrer, Studenten, Räume, Gebäude, …), Logistik (LKW, Fahrer, Ware, Ziel, …)
Warum ist es so schwierig ein leistungsfähiges Schachprogramm zu entwerfen?
Deep Blue war ein von IBM entwickelter Schachcomputer.
Enorme Rechenleistung (Version 1996 - 36 Knoten und 216 Chips - Version 1997 - 30 Knoten mit 480 Chips). Jeder Knoten verfügte über 1 GB RAM und 4 GB Festplattenspeicher. Berechnet wurden je nach Stellungstyp zwischen 100 und 200 Millionen, im Durchschnitt 126 Millionen Stellungen pro Sekunde. Von $10^{43}$ möglichen.
Kasparow konnte das erste Match, das mit sechs Partien von 1996 in Philadelphia stattfand, für sich entscheiden. Er gewann drei Partien, machte zwei Remis und verlor eine Partie, womit er Deep Blue 4:2 schlug. Anschließend rüstete IBM seine Maschine mit stärkerer Hardware aus und trat im Mai 1997 erneut gegen Kasparow an. Deep Blue, der mittlerweile 200 Millionen Stellungen pro Sekunde berechnen konnte, gewann die Revanche 3,5:2,5
Schachcomputer - Parameter:
Bewertungsfunktion bestand aus der in Hardware ausgeführten umfangreichen Parameterauswertung und der in Software ausgeführten Gewichtung dieser Parameter (z. B.: wie wichtig ist die Königssicherheit im Vergleich mit einem Raumvorteil im Zentrum). Die optimalen Werte der Parameter wurden vom System selbst bestimmt, indem es Tausende von Meisterpartien analysierte. Vor dem zweiten Match wurde das Schachwissen des Programms von Großmeister Joel Benjamin optimiert.
Seite 6
Abzählbar unendliche Menge
Eine Menge $M$ heißt abzählbar unendlich, wenn sie zur Menge $N$ der natürlichen Zahlen gleichmächtig ist. Alle anderen unendlichen Mengen sollen überabzählbar unendlich heißen.
Cantorsches Diagonalisierungsverfahren 1. Art
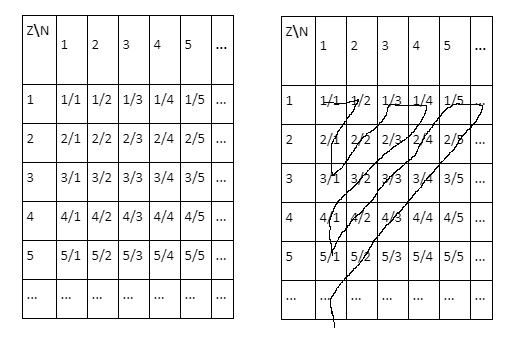
Versuch ein Ordnungsprinzip für abzählbar unendliche Mengen $M$ anzugeben, mittels einer Druchnummerierung der Elemente, die die geforderte bijektive Abbildung $\mathbf{N} \longmapsto M$ definiert
Die ganzen Zahlen $Z$
Die Menge $Z$ ist abzählbar, denn
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | −1 | 2 | −2 | 3 | −3 | … | n | −n | … |
ist eine Aufzählung von $ℤ$.
Die rationalen Zahlen $Q$
Primzahlen
Die Menge der Primzahlen $P$ ist ebenfalls abzählbar unendlich, da sie eine Teilmenge der natürlichen Zahlen und nach dem Satz von Euklid (unendlich viele Primzahlen) auch unendlich ist.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | … |
Wenn $M_1, M_2, M_3, ...$ abzählbare Mengen sind, dann ist auch die Menge $\bigcup^\infty_{n=1} M_n$ abzählbar.
"ausschroten"...
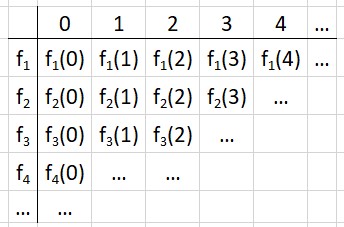
Wenn $M_1, M_2, M_3, ...$ abzählbare Mengen sind
Definition: abzählbare Mengen -> bijektive Abbildung der natürlichen Zahlen auf die Menge
-> es gibt also Funktionen die die natürlichen Zahlen abbilden auf die Menge(n)
Bsp: $f_i: \mathbf{N} \longmapsto M_i$
$f_2(3) = M_23$
Funktion $f_2(3)$ gehört zu Menge $M_2$ und ist das $3$ Element
Seite 9
Seite 13
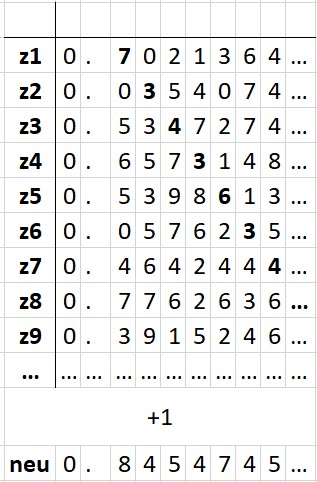
Cantorsches Diagonalisierungsverfahren 2. Art Auflistung aller Elemente der Menge $M$, als sei diese abzählbar unendlich. Anschließender Versuch zu zeigen, dass ein einziges Element aus $M$ nicht vorkommt, sodass sich ein Wiederspruch ergibt.
Zeigen Sie, dass die Menge der reellen Zahlen $R$ überabzählbar unendlich ist.
Beschränkung auf Intervall $[0, 1]$
Das 2. Cantors Diagonalverfahren zeigt, dass so eine Liste nicht alle reellen Zahlen umfassen kann.
Die Menge $R$ ist überabzählbar.