Vorlesung 2 Belkouchi

Aus ProgrammingWiki

Folie 8

[[ ÜA:Zeigen Sie, dass die folgenden Mengen abzählbar unendlich sind: Z,Q, die Menge der Primzahlen, die geraden Zahlen. ]]

Nehmen wir die Funktion  : f:N↦Z mit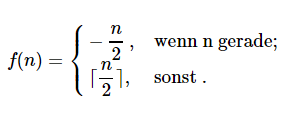

Für Z:

So wurde gezeigt, dass die ganzen Zahlen abzählbar unendlich sind.

mit Hilfe das Cantorschen Diagonalisierungsverfahren :

Für die Menge der Primzahlen:

. nach Satz von Euklid, Die Menge der Primzahlen P ist unendlich. . Die Menge der Primzahlen P ist abzählbar unendlich, so gilt: P ⊂N.

Für die Menge der geraden Zahlen:

. per Definition sind die geraden Zahlen unendlich und abzählbar unendlich, so gilt: G ⊂Z.

Folie 9

Verifizieren Sie, dass die folgende Funktion f:N+→Q+ eine bijektive Funktion ist und implementieren Sie eine Prozedur, die die zugehörige Umkehrfunktion f−1 berechnet.

function f(n){ if(n===1) return 1; if(n%2==0) return (f(n/2)+1); return (1/(f(n-1))); }

f(1);

ausführen

Berechnen Sie f(n) für n = 1, 2, . . . , 7 mit der Hand:

f(1)=1

f(2)=2

f(3)=0,5

f(4)=3

f(5)=13

f(6)=1,5

f(7)=23

Folie 13

Zeigen Sie, dass die Menge überabzählbar unendlich ist:

Annahme: R ist abzählbar unendlich. Die Realen Zahl werden wie folgenden geschrieben :

Nehmen wir an, die reellen Zahlen wären abzählbar, dann wären sicher auch die Zahlen im Intervall [0,1][0,1] abzählbar unendlich. Nehmen wir an, wir hätten eine Abzählung in Dezimalbruchschreibweise: