Vorlesung 1 Grüning
Aus ProgrammingWiki
Wahrheitstabellen
Direkte Beweise:
z.z. Wenn $n \in \mathbf{N}$ ungerade, dann $n^2$ ungerade
$n = 2k + 1 | k \in \mathbf{N}$
$(2k+1)^2 = (2k+1)(2k+1) = 4k^2 + 2k + 2k + 1 = 4k^2 + 4k + 1 = 2(2k^2 + 2k) + 1$
$=>$ Erster Summand ist gerade, da er den Faktor 2 enthält, durch das +1 wird der Term immer ungerade $=>$ Wenn n in N ungerade, dann $n^2$ ungerade
z.z Die Summe dreier aufeinanderfolgender natürlicher Zahlen ist stets durch 3 teilbar.
$n \in \mathbf{N}$
$n + (n + 1) + (n + 2) = 3n + 3 = 3(n + 1) | (n + 1) \in \mathbf{N}$
Aquivalenzrelationen:
symmetrisch: $\forall x \forall y$ wenn aus x R y stets y R x folgt
reflexiv: wenn jedes Element zu sich selbst in Relation steht
transitv: wenn a R b und b R c dann a R c (z.B. a < b und b < c dann a < c)
Beispiel Gleichheit:
x = y -> y = x (symmetrisch)
x = x (reflexiv)
x = y und y = z dann x = z (transitiv)
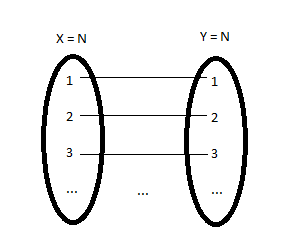
Satz: Eine Menge M ist entweder endlich oder abzählbar unendlich, wenn es eine surjektive Funktion $\mathbf{N} \rightarrow M$ gibt.
Beweis: Wenn M abzählbar unendlich ist kann diese surjektive Funktion auch zu einer bijektiven gemacht werden, da jede bijektive Funktion auch surjektiv ist und damit könnte man die Definition der abzählbar unendlichen Menge abdecken. Wenn M endlich ist kann man |M| Äquivalenzklassen in $\mathbf{N}$ (z.B. mod |M|) bilden wobei alle Elemente in einer Äquivalenzklasse auf das gleiche Element aus M zeigen.
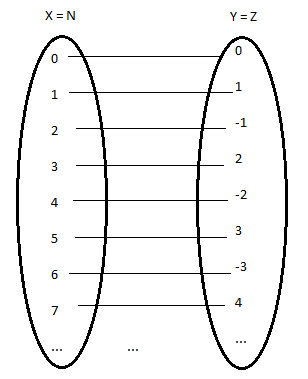
z.z. Zeigen Sie, dass die Menge $\mathbf{Z}$ eine abzählbar unendliche Menge ist.
Wenn man die Menge $\mathbf{N}$ auf sich selbst als bijektive Funktion abbildet könnte man jede Zahl aus der Menge X der gleichen Zahl aus Y zuweisen:
Bei $\mathbf{Z}$ rückt man nun jedes Element ($>1$) an eine neue Stelle und zwar $n - 1$ Stellen weiter, damit die vorherigen negativen Zahlen "noch Platz haben". Also Listet man die positive Zahl und dannach das negative Äquivalent: