Vorlesung 11 Merkelt

Aus ProgrammingWiki

Inhaltsverzeichnis 1 Folie 6 2 Folie 16 3 Folie 32 4 Folie 35 5 Folie 39 6 Folie 41 6.1 Fakultät 6.2 Abstandsfunktion 7 Folie 45 (1) 8 Folie 45 (2)

Folie 6

$mult(0, n) = 0$

$mult(S(m), n) = add(mult(m, n), n)$

$pot(0, n) = 1$

$pot(S(m), n) = mult(pot(m, n), n)$

Folie 16

$S^2_*(q,m) = S(S(...S(m))...)$

Nach Schema:

$S^2_*(0,m) = f(m)$

$S^2_*(S(n),m) = g(n,h(n,m),m)$

$f(m) = U^1_1(m) = m$

$g(a,b,c) = S(U^3_2(a,b,c))$

$h(n,m) = S^2_*(n,m)$

finale $\mu$-rekursive Vorschrift:

$S^2_*(0,m) = U^1_1(m) = m$

$S^2_*(S(n),m) = S(U^3_2(n,S^2_*(n,m),m))$

Folie 32

Nur die Tabellen benutzen:

nr	0	1	2	3	4	5	6	7	8	9	10
0	1	2	3	4	5	6	7	8	9	10	11
1	2	3	4	5	6	7	8	9	10	11
2	3	5	7	9	11
3	5
4
5

Mit Schema weiter verfolgen:

nr	0	1	2	3	4	5	6	7	8	9	10
0	1	2	3	4	5	6	7	8	9	10	11
1	2	3	4	5	6	7	8	9	10	11	12
2	3	5	7	9	11	13	15	17	19	21	23
3	5	13	29	61	125	253	509	1021	2045	4093	8189
4	13
5

Bildungsvorschriften:

(0) $m + 1$

(1) $m + 2$

(2) $2m + 3$

(3) $2^{m+3} - 3$

Folie 35

Folie 39

Folie 41

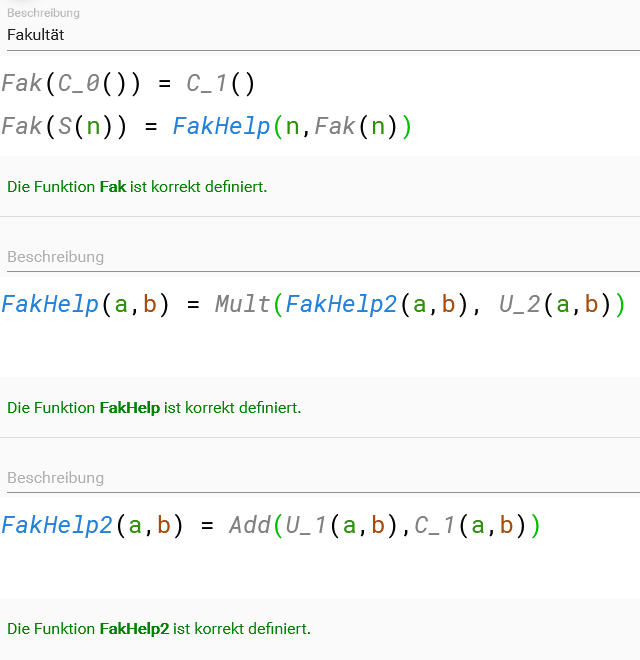
Fakultät

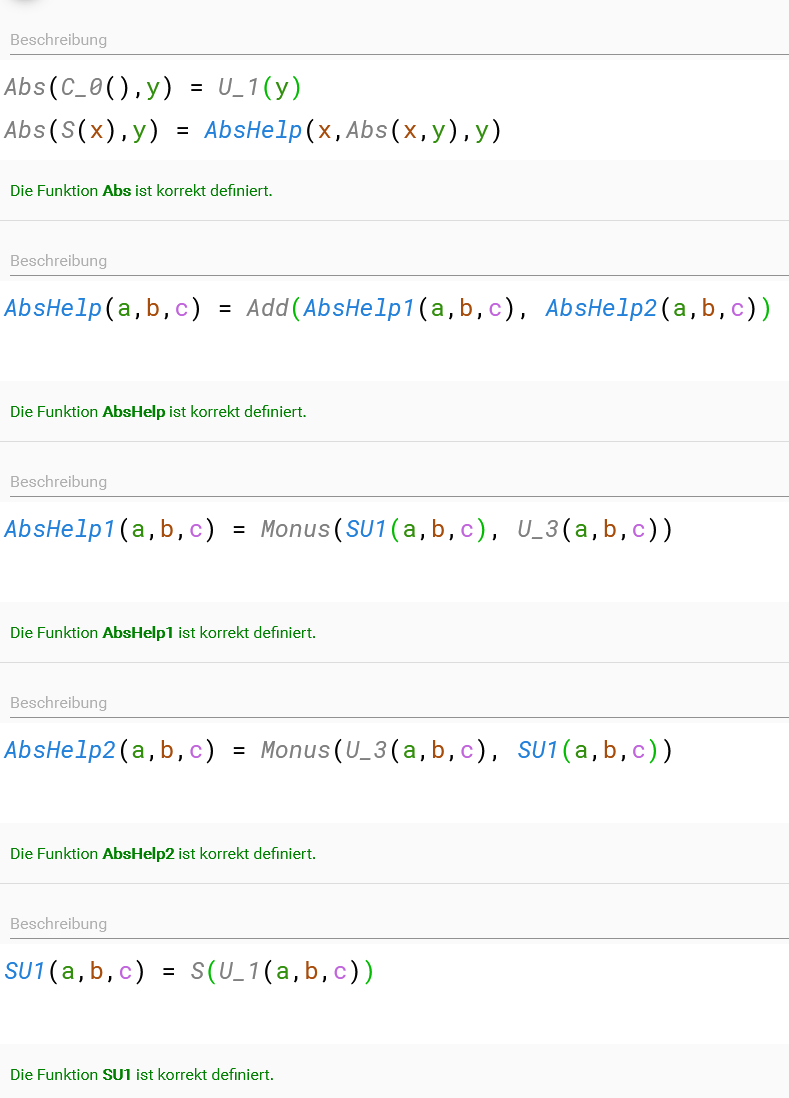
Abstandsfunktion

Folie 45 (1)

Folie 45 (2)

$F_1(4,6) = F_0(F_1(4,5),F_1(4,5)+5+1) = F_0(185,191) = 376$

$F_1(4,5) = F_0(F_1(4,4),F_1(4,4)+4+1) = F_0(90,95) = 185$

$F_1(4,4) = F_0(F_1(4,3),F_1(4,3)+3+1) = F_0(43,47) = 90$

$F_1(4,3) = F_0(F_1(4,2),F_1(4,2)+2+1) = F_0(20,23) = 43$

$F_1(4,2) = F_0(F_1(4,1),F_1(4,1)+1+1) = F_0(9,11) = 20$

$F_1(4,1) = F_0(F_1(4,0),F_1(4,0)+0+1) = F_0(4,5) = 9$

$F_1(4,0) = 4$

$F_2(2,1) = F_1(F_2(2,0),F_2(2,0)+0+1) = F_1(2,3) = 27$

$F_2(2,0) = 2$

$F_1(2,3) = F_0(F_1(2,2),F_1(2,2)+2+1) = F_0(12,15) = 27$

$F_1(2,2) = F_0(F_1(2,1),F_1(2,1)+1+1) = F_0(5,7) = 12$

$F_1(2,1) = F_0(F_1(2,0),F_1(2,0)+0+1) = F_0(2,3) = 5$

$F_1(2,0) = 2$