Begriffssammlung
Aus ProgrammingWiki
Inhaltsverzeichnis |
TODO
- Sätze mit aufnehmen, Beweise?
Menge
Eine Sammlung verschiedener Elemente (engl. "A set is a collection of distinct elements").
Zwei Mengen sind genau dann gleich, wenn sie genau die selben Elemente enthalten.
Die leere Menge ($\emptyset$ oder $\{\}$) ist die Menge, die keine Elemente hat.
Darstellung
Das Euler-Diagramm versucht, Mengen zu veranschaulichen, indem sie als Schlaufen gezeichnet werden, die ihre Elemente umschließen. Ist eine Menge Teilmenge einer anderen, dann liegt ihre Schlaufe vollständig innerhalb der der enthaltenden Menge.
Das Venn-Diagramm versucht, alle Zugehörigkeits-Möglichkeiten für die Elemente von $n$ beliebigen Mengen aufzuzeigen. Dabei spielt es keine Rolle, ob einige Bereiche für eine Belegung konkreter Mengen gar keine Elemente enthalten. Es entstehen $n^2$ Zonen, die alle Möglichkeiten repräsentieren.
(siehe en.wikipedia.org/wiki/Set_(mathematics)#Euler_and_Venn_diagrams)
Funktion
Eine Funktion ist eine Relation zwischen zwei Mengen $A$ und $B$, die Elemente aus $A$ auf Elementen von $B$ abgebildet.
$f: A \rightarrow B$
$f: x \mapsto y$
$f(x) = y$
$(x, y) \in f$
total und partiell
Eine Funktion $f: X \rightarrow Y$ mit $D_{\!f} = X$ heißt total.
Gilt $D_{\!f} \subseteq X$, ist $f$ eine partielle Funktion.
Hieraus folgt, dass alle totalen Funktionen in der Menge der partiellen Funktionen enthalten sind. Man kann also sagen, dass jede totale Funktion partiell ist, aber nicht umgekehrt.
Injektivität
Eine Funktion ist injektiv, wenn jedem Element der Zielmenge höchstens ein Funktionsargument zugeordnet wurde – die Zuordnung also ein-eindeutig ist.
Ist eine Funktion injektiv, muss gelten: $f(x_1) = y = f(x_2) \Longrightarrow x_1 = x_2$
Surjektivität
Eine Funktion ist surjektiv, wenn jedem Element der Zielmenge mindestens ein Funktionsargument zugeordnet wurde – also jedes über die Zuordnung erreichbar ist und keines ausgelassen wird.
${\large\forall} y \in R \hspace{10px} {\large\exists} x \in D : \hspace{8px} f(x) = y \hspace{1cm}$ (wobei $R$ die Bildmenge und $D$ der Definitionsbereich sind)
Bijektivität
Eine Funktion ist bijektiv, wenn sie sowohl injektiv als auch surjektiv ist, wenn auf jedes Element der Zielmenge genau ein Funktionsargument abgebildet wird.
Eigenschaften von Mengen
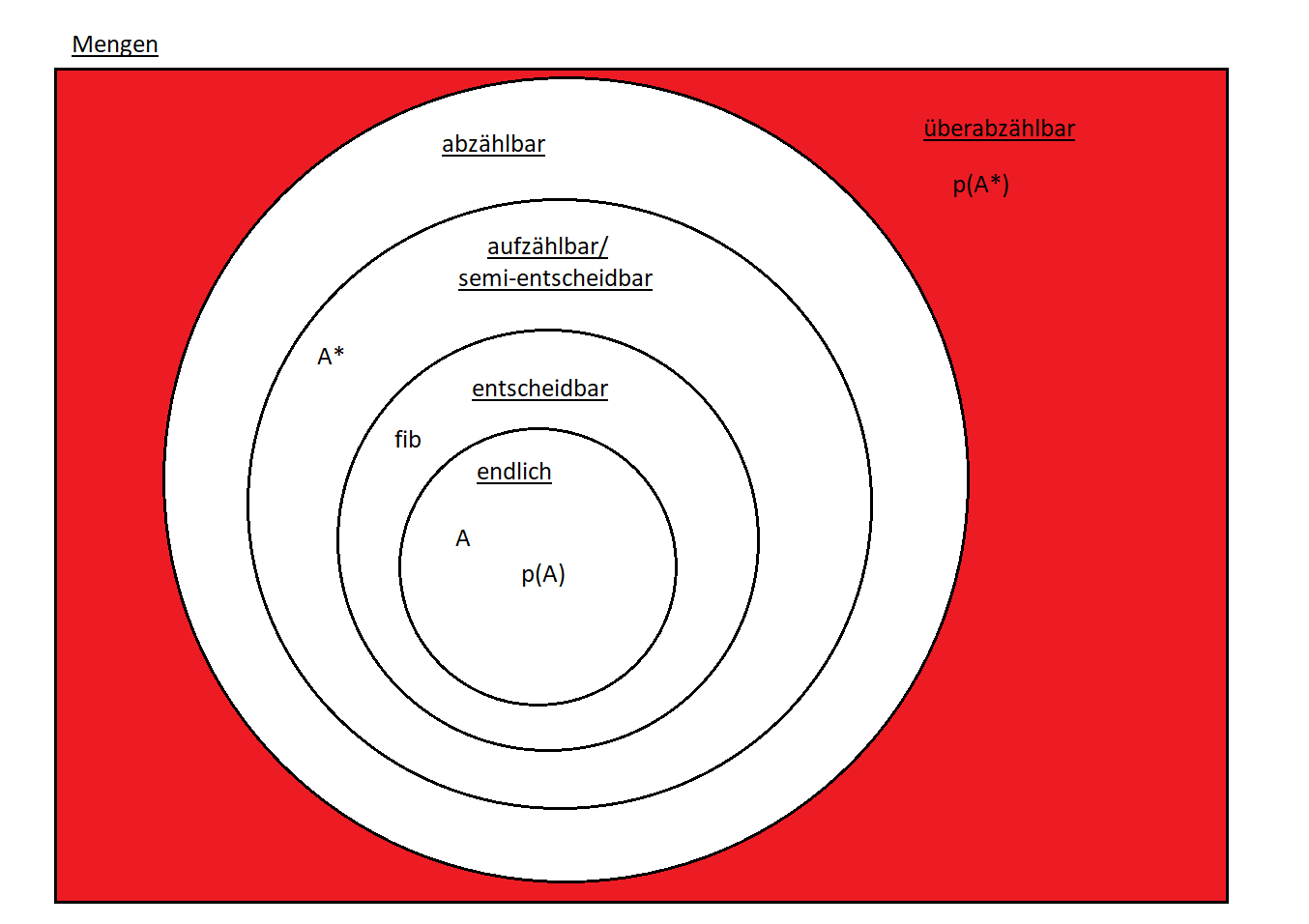
Abzählbarkeit
Eine unendliche Menge $M$ heißt abzählbar unendlich, wenn es eine bijektive Funktion $\mathbb{N} \rightarrow M$ gibt. Gibt eine solche Funktion nicht, so ist $M$ überabzählbar unendlich.
Aufzählbarkeit
Eine Menge $M \subseteq A^\ast$ heißt (rekursiv) aufzählbar (engl. recursively enumerable), wenn es entweder eine total berechenbare surjektive Funktion $f: \mathbb{N} \rightarrow M$ gibt, oder es gilt $M = \emptyset$. Man nennt $f$ eine Aufzählprozedur oder ein Aufzählverfahren von $M$.
Satz: Eine Menge $M$ ist genau dann aufzählbar, wenn sie semi-entscheidbar ist.
Satz: Jede Teilmenge einer abzählbaren Menge ist abzählbar, aber nicht jede Teilmenge einer aufzählbaren Menge ist aufzählbar.
Semi-entscheidbarkeit
Eine Menge $M \subseteq A^\ast$ ist (absolut) semi-entscheidbar, wenn die partielle (semi-charakteristische) Funktion $\chi'_M : A^\ast \rightarrow \{wahr\}$ mit: \[ \chi'_M(w) = \begin{cases} wahr, & \mbox{wenn } \mbox{$w \in M$;} \\ \perp, & \mbox{sonst.}\end{cases} \] berechenbar ist.
Turing-aufzählbar
Eine Menge $M \subseteq A^\ast$ heißt (rekursiv) Turing-aufzählbar (engl. recursively enumerable), wenn es entweder eine total Turing-berechenbare surjektive Funktion $f: \mathbb{N} \rightarrow M$ gibt, oder es gilt $M = \emptyset$. Man nennt $f$ eine Aufzählprozedur oder ein Aufzählverfahren von $M$.
Entscheidbarkeit
Eine Menge $M \subseteq A^\ast$ ist (absolut) entscheidbar, wenn $M$ zu $A^\ast$ relativ entscheidbar ist, d.h. wenn $\chi_{M, A^\ast}$, kurz: $\chi_M$, mit \[ \chi_M(w) = \begin{cases} wahr, & \mbox{wenn } \mbox{$w \in M$} \\ falsch, & \mbox{wenn } \mbox{$w \in A^\ast \setminus M$} \end{cases} \] eine total berechenbare Funktion ist.
Satz: Wenn die Menge $M$ entscheidbar ist, dann ist $M$ aufzählbar. (Die Umkehrung dieses Satzes gilt nicht!)
Satz: Eine Menge $M$, mit $M \subseteq A^\ast$, ist entscheidbar genau dann, wenn $M$ und $A^\ast \backslash M$ (Komplementmenge) aufzählbare Mengen sind.
Turing-entscheidbar
Eine Menge $M \subseteq A^\ast$ ist (absolut) Turing-entscheidbar, wenn $M$ zu $A^\ast$ relativ entscheidbar ist, d.h. wenn $\chi_{M, A^\ast}$, kurz: $\chi_M$, mit \[ \chi_M(w) = \begin{cases} wahr, & \mbox{wenn } \mbox{$w \in M$} \\ falsch, & \mbox{wenn } \mbox{$w \in A^\ast \setminus M$} \end{cases} \] eine total Turing-berechenbare Funktion ist.
Eigenschaften von Funktionen
Berechenbarkeit
Eine Funktion $f$ ist berechenbar, wenn es einen Algorithmus gibt, der für jedes $x \in D_{\!f}$ den zugehörigen Funktionswert $f(x)$ effektiv ermittelt. ("effektiv" = es muss ein entsprechendes Verfahren geben)
Turing-Berechenbarkeit
Eine Funktion $f: \sum^\ast \rightarrow \sum^\ast$ heißt Turing-berechenbar, wenn es eine (deterministische) Turing-Maschine $M$ gibt, so dass für alle $w, y \in \sum^\ast$ gilt: $f(w) = y$ genau dann, wenn $q_0\ w \stackrel{\ast}{\vdash} q_e\ y, q_e \in E$.