Brainstorming
Aus ProgrammingWiki
Inhaltsverzeichnis |
Prinzipiell Unlösbares (für Computer)
(Für Computer) unzugängliches
- Einschätzung eines sich spontan ändernden Systems
- Subjektive Wertveränderungen einordnen
Praktisch Unmögliches
- eindeutige Vorhersage zur Endlichkeit und ggf. zum Endzustand eines unbekannten, nicht-deterministischen Automaten
Abzählbarkeit
$\mathbb{Q}$
$\mathbb{R}$
Wenn $\mathbb{R}$ überabzählbar unendlich wäre, dann müsste man in der Lage sein, für $x, y \in \mathbb{R}$, mit $x < y$ eine Funktion $x' = f(x)$ zu definieren, für die immer gilt: $x < x'_1 = f(x) < x'_2 = f(x'_1) < x'_3 = f(x'_2) < ... x'_\infty < y$. Anders gesagt: $y$ ist indirekter Nachfolger von $x$. Wenn es eine Funktion gibt, die unendlich viele indirekte Nachfolger von $x$ produziert, die gleichzeitig indirekte Vorgänger von $y$ sind, dann ist die Überabzählbarkeit gezeigt, da $y$ nie "erreicht" wird.
Solch eine Funktion gibt es: $f(x) = \frac{x}{10} + 0,1$.
$x = 0,11; y = 0,12$
$x'_1 = f(x) = 0,111$
$x'_2 = f(x'_1) = 0,1111$
$x'_3 = f(x'_2) = 0,11111$
$x'_4 = f(x'_3) = 0,111111$
$x'_5 = f(x'_4) = 0,1111111$
$x'_6 = f(x'_5) = 0,11111111$
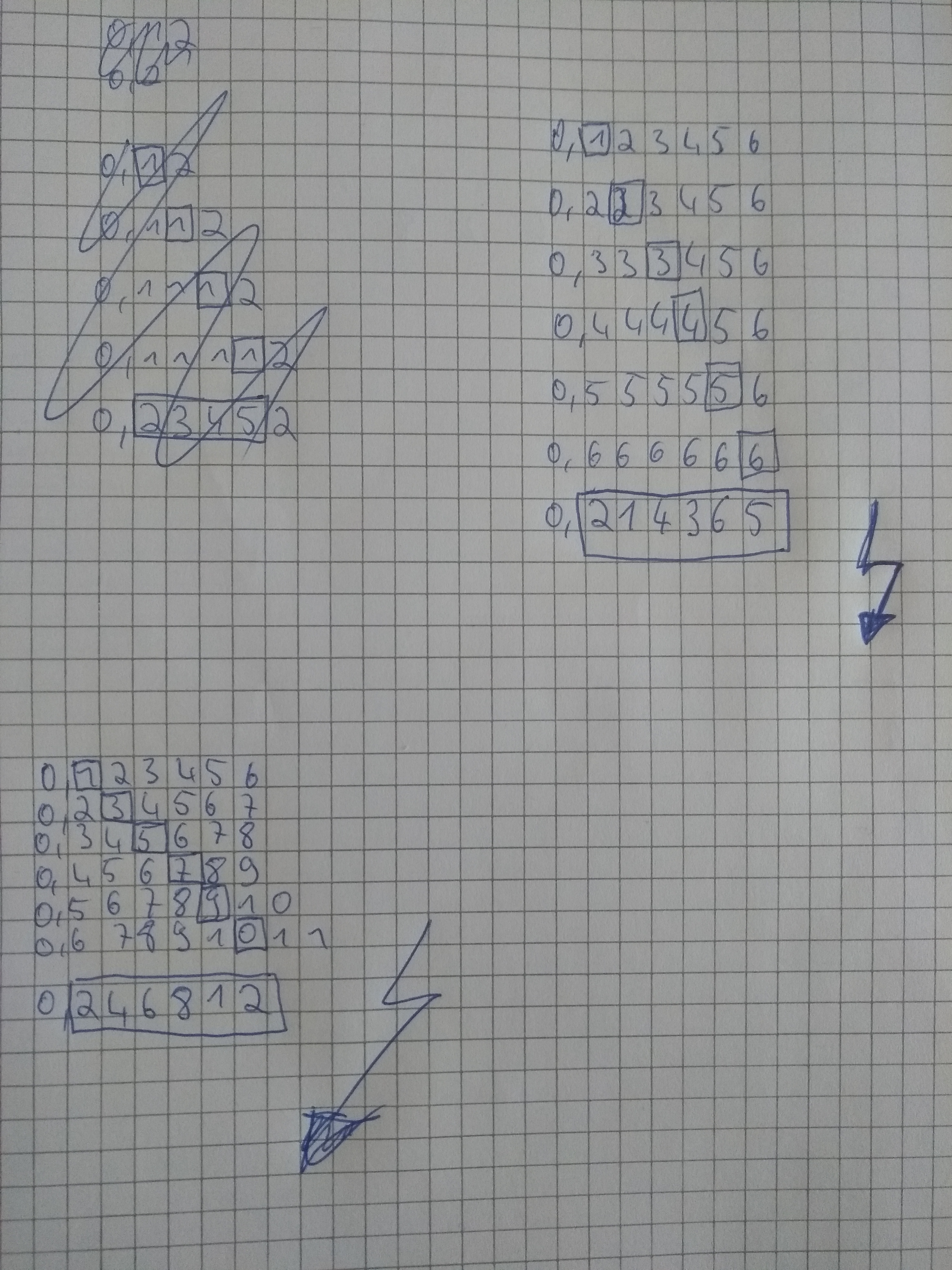
Soviel zur Überlegung. Hier das 2. cantorsche Diagonalargument:
Hilberts Hotel
Ein Hotel mit unendlich vielen Zimmern seht an der Straße.
Fall 1: Ein Gast tritt an den Rezeptionisten heran:
G: Ich hätte gern ein Zimmer.
R: Im Moment sind unendlich viele Gäste da, jedoch kann ich Ihnen gern ein Zimmer frei machen.
R funkt mit seinem magischen Funkgerät, welches ohne Verzögerung sendet, zu den magischen Empfängern, die ohne Verzögerung empfangen, von denen je einer in jedem Zimmer angebracht ist: Bitte alle ein Zimmer weiter rutschen!
R: So, das erste Zimmer ist frei für Sie, bitteschön.
Fall 2: Ein Bus hält am Hotel. Der Busfahrer spricht mit dem Rezeptionisten.
B: Ich habe hier unendlich viele Gäste, von denen jeder ein Zimmer braucht.
R: Im moment sind unendlich viele Gäste da, jedoch kann ich gern unendlich viele Zimmer für unendlich viele Gäste gleichzeitig frei machen.
R funkt mit seinem magischen Funkgerät, welches ohne Verzögerung sendet, zu den magischen Empfängern, die ohne Verzögerung empfangen, von denen je einer in jedem Zimmer angebracht ist: Bitte alle aus dem Zimmer treten, die eigene Zimmernummer mit zwei multiplizieren und in dieses Zimmer gehen!
Nun sind alle bisherigen Gäste in den Zimmern mit gerader Nummer untergebracht und die ankommenden Gäste können in den Zimmern mit ungerader Nummer untergebracht werden.
Fall 3: Zwei Gäste treten an den Rezeptionisten heran:
G1: Ich brauche ein Zimmer, jedoch bin ich eine gespaltene Persönlichkeit mit unendlich vielen Persönlichkeiten. Jede Persönlichkeit benötigt ein Bett.
R: Im Moment sind unendlich viele Gäste da, jedoch kann ich Ihnen gern ein Zimmer frei machen. Anschließend mache ich noch ein Zimmer frei und wir schaffen einen Durchbruch zu Ihrem Zimmer, dann haben Sie ein Bett mehr für eine weitere Ihrer Persönlichkeiten. Und so machen wir immer weiter.
R beginnt zu funken.
G2 ist nun obdachlos.
Schachcomputer
Einen leistungsfähigen Schachautomaten zu schreiben ist deshalb keine leichte Aufgabe, weil die Zugfolgen des (Menschlichen) Gegenspielers nicht deterministisch sind, ein Schachcomputer jedoch viele Zugfolgen voraus errechnen und diese demzufolge alle durchspielen muss, bevor die nächsten sinnvollen Züge geplant werden können. Beispielüberschlagsrechnung: im schlimmsten Fall könnten alle 16 der gegnerischen Figuren potenziell bewegt werden, mit rund 3 verschiedenen Möglichkeiten der Zuggestaltung pro Figur. Wollte man 10 Züge voraus rechnen, ergäben sich etwa gegnerische Züge, mit im schlimmsten Fall ebenfalls
möglichen Antworten mit den eigenen Figuren. Ganz so dramatisch ist es mit einer tatsächlichen Schachpartie wohl nicht, dennoch wird für außergewöhnliche Leistung auf fortgeschrittene Konzepte, wie z.B. Deep-Learning oder Reinforcement-Learning, möglicherweise mit eingebauter, künstlicher spontanität (Pseudozufallsaktionen) zurückgegriffen.