Vorlesung 1
Aus ProgrammingWiki

Inhaltsverzeichnis |
Indirekter Beweis
Aufgabe 1
Beweisen Sie indirekt, dass $x$ eine gerade Zahl ist, wenn $x^2$ eine gerade Zahl ist. Wobei $x \in{\N}$.
z.z. Wenn $x^2$ gerade, dann $x$ gerade. $x \in{\N}$
Annahme: Wenn $x^2$ gerade, dann $x$ ungerade.
Beweis
$A$ = $x^2$ ist gerade
$B$ = $x$ ist gerade
| $A$ | $B$ | $\overline{A}$ | $\overline{B}$ | $A \Rightarrow B$ | $A \Rightarrow \overline{B}$ | $\neg(A \Rightarrow B)$ | Info |
|---|---|---|---|---|---|---|---|
| W | W | F | F | W | F | F | fällt weg, weil $\overline{B}$ falsch |
| W | F | F | W | F | W | W | |
| F | W | W | F | W | W | F | fällt weg, weil $A$ falsch |
| F | F | W | W | W | W | F | fällt weg, weil $A$ falsch |
In der zweiten Zeile wird der Widerspruch deutlich:
Sowohl die Annahme $A \Rightarrow \overline{B}$ ($x$ ist ungerade, wenn $x^2$ gerade ist)
als auch die Aussage $\neg(A \Rightarrow B)$ (Wenn $x^2$ nicht gerade ist, dann ist $x$ nicht gerade.)
sind wahr. Damit wäre $x$ gleichzeitig gerade und ungerade, wenn $x^2$ eine gerade Zahl ist.
Damit ist die Annahme falsch und bewiesen, dass $x$ eine gerade Zahl ist, wenn $x^2$ eine gerade Zahl ist.
Aufgabe 2 und 3
2) Beweisen Sie die Aussage, wonach aus der Gültigkeit der Aussagen $A \Rightarrow B$, $B \Rightarrow C$ und $\overline{C}$ die Gültigkeiten von $\overline{A}$ und $\overline{B}$ folgen. Stellen Sie den Sachverhalt in einer Wahrheitstafel dar.
3) Was kann man aus der Gültigkeit von $A$ und $B$ schließen, wenn bekannt ist, dass $A \Rightarrow B$, $B \Rightarrow C$ und $C$ gelten?
Verwenden Sie die Tafel aus Aufgabe 2.
| Zeile | $A$ | $B$ | $C$ | $\overline{A}$ | $\overline{B}$ | $\overline{C}$ | $A \Rightarrow B$ | $B \Rightarrow C$ | 2 | 3 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | W | W | W | F | F | F | W | W | x | |
| 2 | W | W | F | F | F | W | W | F | ||
| 3 | W | F | W | F | W | F | F | W | ||
| 4 | W | F | F | F | W | W | F | W | ||
| 5 | F | W | W | W | F | F | W | W | x | |
| 6 | F | W | F | W | F | W | W | F | ||
| 7 | F | F | W | W | W | F | W | W | x | |
| 8 | F | F | F | W | W | W | W | W | x |
Lösung Aufgabe 2:
Nur in Zeile 8 gelten sowohl $A \Rightarrow B$, $B \Rightarrow C$ und $\overline{C}$.
Damit geht einher, dass dort $\overline{A}$ und $\overline{B}$ gelten.
Lösung Aufgabe 3:
In den Zeilen 1,5 und 7 sind die Aussagen $A \Rightarrow B$, $B \Rightarrow C$ und $C$ gültig.
Die daraus folgenden Gültigkeiten für $A$ und $B$ sind folgende:
- $A$ und $B$ sind gültig
- $A$ gilt nicht, aber $B$ gilt
- $A$ und $B$ gelten beide nicht
Daraus folgt, dass es den Fall $A$ gilt, aber $B$ gilt nicht, nicht geben kann.
Äquivalenzrelationen
Aufgabe: Wiederholen Sie die Eigenschaften von Aquivalenzrelationen und geben Sie ein Beispiel an.
Äquivalenzrelationen besitzen drei Eigenschaften:
- Reflexivität $a \sim a$ (Jedes Objekt ist zu sich selbst äquivalent.)
- Symmetrie $a \sim b \Rightarrow b \sim a$ (Wenn $a$ äquivalent zu $b$ ist, dann ist auch $b$ äquivalent zu $a$.)
- Transitivität $a \sim b$ und $b \sim c$ $\Rightarrow$ $a \sim c$ (Wenn $a$ äquivalent zu $b$ und $b$ äquivalent zu $c$ ist, dann ist auch $a$ äquivalent zu $c$.)
Beispiel
Bücheridentifikation anhand der ISBN-Nummern
- reflexiv: Ein Buch hat genau eine ISBN, die sich nicht ändert und eindeutig ist. Daher hat ein Buch a die gleiche ISBN wie Buch a.
- symmetrisch: Wenn Buch a die gleiche ISBN wie Buch b hat, dann hat auch Buch b die gleiche ISBN wie Buch a.
- transitiv: Wenn Buch a die gleiche ISBN wie Buch b hat und Buch b die gleiche ISBN wie Buch c hat, hat auch Buch a die gleiche ISBN wie Buch c.
Funktionen
Partielle Funktion
$q(x)=\begin{cases} \dfrac{35}{x-3}, & \text{wenn }x \neq 3\text{;}\\ \bot, & \text{sonst.} \end{cases} $
Aufgabe: Schreiben Sie ein Programm, das $q$ berechnet.
Aufgabe 2
Geben Sie sich einige Definitionsbeispiele selbstgewählter Funktionen vor. Achten Sie darauf, dass es sich auch um (echte) partielle Funktionen handeln kann. Außerdem sollten Sie einige abschnittsweise definierte Funktionen, z.B. Briefporto, Zuzahlungen für Medikamente usw., aufnehmen.
Beispiel Briefporto:
$briefporto(g) = \begin{cases} 0.62, & \text{wenn } g \leq 20\\ 0.85, & \text{wenn } 20 \lt g \leq 50\\ 1.45, & \text{wenn } 50 \lt g \leq 500\\ 2.40, & \text{wenn } 500 \lt g \leq 1000\\ \bot,&\text{sonst.} \end{cases}$
Aufgabe 3
Wiederholen Sie die folgenden Eigenschaften von Funktionen: injektiv, surjektiv und bijektiv.
Geben Sie aussagekräftige Beispiele an. Skizzieren Sie folgende Funktionen mittels Abbildungspfeilen aus X in Y : injektiv und surjektiv; injektiv, nicht surjektiv; nicht injektiv, surjektiv; nicht injektiv, nicht surjektiv.
injektiv = linkseindeutig, jedes Element in der Zielmenge wird höchstens ein Mal getroffen
surjektiv = rechtstotal, jedes Element in der Zielmenge wird mindestens ein Mal getroffen
bijektiv = eineindeutig, jedes Element in der Zielmenge wird genau ein Mal getroffen
| Eigenschaften | Abbildung |
|---|---|
| injektiv und surjektiv | 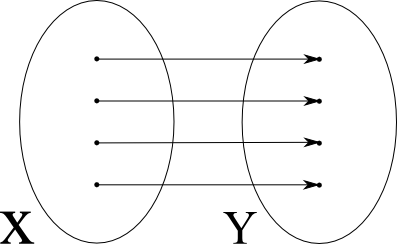
|
| injektiv, nicht surjektiv | 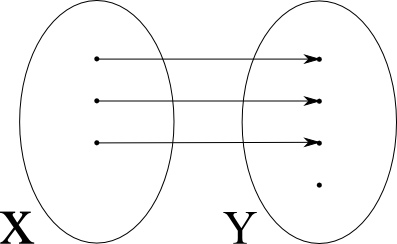
|
| nicht injektiv, surjektiv | 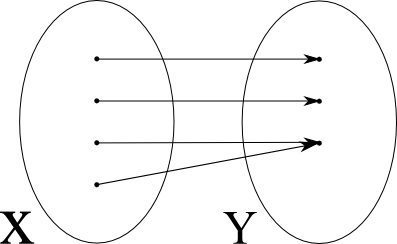
|
| nicht injektiv, nicht surjektiv | 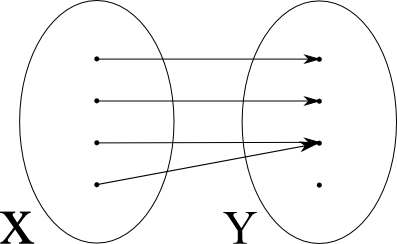
|
Mengen
Abzählbar unendlich
Zeigen Sie, dass die Menge Z eine abzählbar unendliche Menge ist und setzen Sie sich mit der Aussage auseinander, wonach doch $\Z$ eigentlich doppelt so viele Elemente besitzt wie $\N$.
z.z.: $\Z$ ist eine abzählbar undendliche Menge, d.h. es existiert eine Funktion $f$, die $\N$ auf $\Z$ bijektiv abbildet. $f: \N \rightarrow \Z$
$f(n) = \begin{cases} \frac{n}{2}, \text{wenn n gerade}\\ -\frac{n+1}{2}, \text{sonst}. \end{cases}$
Potenzmenge
Entwerfen Sie ein Aufbauschema zur systematischen Erzeugung aller Elemente aus $\wp(M)$ für eine gegebene endliche Menge $M$ und wenden Sie es auf einige selbstgewählte Beispiele an.
Die Potenzmenge $\wp$ einer Menge $M$ ist die Menge aller Teilmengen von $M$.
Beispielhafte Menge $M$: $M = \{a,b,c,d\}$
Die zugehörige Potenzmenge ist $\wp(M) = \{\emptyset, \{a\},\{b\},\{c\},\{d\},\{a,b\},\{a,c\},\{a,d\}, \{b,c\}, \{b,d\}, \{c,d\}, \{a,b,c\}, \{a,b,d\}, \{a,c,d\}, \{b,c,d\}, \{a,b,c,d\}\}$
Aufbauschema
- 1) Füge die Leere Menge hinzu.
- 2) Übernimm die bisherige Menge und füge ein neues Element aus $M$ allen bisher vorhandenen Teilmengen hinzu.
- 3) Wiederhole 2, bis alle Elemente aus $M$ untergebracht sind.
Auf das Beispiel angewendet entsteht so nach dem Schema nach und nach die Potenzmenge:
- 1. Schritt: $\wp(M) = \{\emptyset\}$
- 2. Schritt: $\wp(M) = \{\emptyset, \{a\} \}$
- 3. Schritt: $\wp(M) = \{\emptyset, \{a\}, \{b\}, \{a,b\} \}$
- 4. Schritt: $\wp(M) = \{\emptyset, \{a\}, \{b\}, \{a,b\}, \{c\}, \{a,c\}, \{b,c\}, \{a,b,c\}\}$
- 5. Schritt: $\wp(M) = \{\emptyset, \{a\}, \{b\}, \{a,b\}, \{c\}, \{a,c\}, \{b,c\}, \{a,b,c\}, \{d\}, \{a,d\} ,\{b,d\}, \{a,b,d\}, \{c,d\}, \{a,c,d\}, \{b,c,d\}, \{a,b,c,d\}\}$
Aufbauschema in Java