uebung1
Aus ProgrammingWiki
Inhaltsverzeichnis |
Aufgabe 1
Beweisen Sie indirekt, dass $x$ eine gerade Zahl ist, wenn $x^2$ mit $x \in \mathbb{N}$ eine gerade Zahl ist.
Lösung:
zu zeigen: Wenn $x^2$ gerade ist, dann ist auch $x$ gerade
Annahme: Wenn $2 \mid x^2$, dann $2 \nmid x$
Beweis:
$\Rightarrow (2k+1)^2 = 4k^2 + 4k + 1 \Rightarrow ungerade, da +1$
$\Rightarrow$ Widerspruch, da $x^2$ gleichzeitig gerade und ungerade wäre.
Aufgabe 2
Beweisen Sie die Aussage, wonach aus der Gültigkeit der Aussagen und
die Gültigkeiten von
und
folgen. Stellen Sie den Sachverhalt in einer Wahrheitstabelle dar.
Lösung:
| Zeile | $A$ | $B$ | $C$ | $\overline{A}$ | $\overline{B}$ | $\overline{C}$ | $A \Rightarrow B$ | $B \Rightarrow C$ |
|---|---|---|---|---|---|---|---|---|
| 1 | W | W | W | F | F | F | W | W |
| 2 | W | W | F | F | F | W | W | F |
| 3 | W | F | W | F | W | F | F | W |
| 4 | W | F | F | F | W | W | F | W |
| 5 | F | W | W | W | F | F | W | W |
| 6 | F | W | F | W | F | W | W | F |
| 7 | F | F | W | W | W | F | W | W |
| 8 | F | F | F | W | W | W | W | W |
Nur in Zeile 8 folgen aus der Gültigkeit der Aussagen $A \Rightarrow B$, $B \Rightarrow C$ und $\overline{C}$ die Gültigkeiten von $\overline{A}$ und $\overline{B}$, also wenn $A$, $B$ und $C$ nicht gelten.
Aufgabe 3
Was kann man über die Gültigkeit von und
schließen, wenn bekannt ist, dass
und
gelten?
Verwenden Sie die Tabelle aus der vorhergehenden Aufgabenlösung.
Lösung:
Es ist ersichtlich, dass, wenn bekannt ist, dass $A \Rightarrow B$, $B \Rightarrow C$ und $C$ gelten, $A$ und $B$ entweder beide gelten, beide nicht gelten oder nur $B$, aber nicht $A$ gilt.
Aufgabe 4
Beweisen Sie die folgenden Beziehungen für Fibonacci-Zahlen nach Defintion in obigem Beispiel mittels vollständiger Induktion:
und
für
und
Lösung:
OFFEN
Aufgabe 5
Wiederholen Sie die Eigenschaften von Äquivalenzrelationen und geben Sie ein Beispiel an
Lösung:
Eine Äquivalenzrelation teilt eine Menge restlos in nichtleere und disjunkte (elementfremde) Untermengen, Äquivalenzklassen genannt.
Sie besitzt dabei folgende eigenschaften:
- Reflexivität: $a\sim a$
- Jedes Objekt ist zu sich selbst äquivalent.
- Symmetrie: $a\sim b \ \Rightarrow\ b\sim a$
- Wenn a zu b äquivalent ist, dann ist auch b äquivalent zu a (und umgekehrt).
- Transitivität: $a\sim b\ \mathrm{und}\ b\sim c\ \Rightarrow\ a\sim c$
- Wenn a zu b äquivalent und b zu c äquivalent ist, dann ist a äquivalent zu c.
Beispiel:
Betrachtet sei eine Menge $M$ von Nutztieren in einem landwirtschaftlichen Betrieb. Wir definieren die folgende zweistellige Relation $\sim$ auf M:
Für je zwei Nutztiere x und y aus M soll $x \sim y$ genau dann gelten, wenn x und y Tiere derselben Art sind.
Für die Kuh $K$ und den Ochsen $O$ gilt $K\sim O$. Für das Huhn $H$ gilt aber nicht $H\sim K$. Die Relation $\sim$ erfüllt die drei Forderungen für Äquivalenzrelationen:
- Reflexivität
- Jedes Tier ist von derselben Art wie es selbst.
- Symmetrie
- Ist ein Tier von derselben Art wie ein zweites, dann ist das zweite auch von derselben Art wie das erste.
- Transitivität
- Wenn $K$ und $O$ Tiere derselben Art sind und ebenso $O$ und $L$ von derselben Art sind, dann sind auch $K$ und $L$ von derselben Art.
Eine Äquivalenzklasse besteht hier aus den Tieren einer Art. Die Rinder bilden eine und die Hühner eine andere Äquivalenzklasse.
Aufgabe 6
Die im Folg. definierte Funktion $q : \R \mapsto \R$ ist an der Stelle $x=3$ undefiniert. Hierfür verwenden wir das Symbol $\bot$.
$$q(x)=\begin{cases} \dfrac{35}{x-3}, & \text{wenn }x \neq 3\text{;}\\ \bot, & \text{sonst.} \end{cases} $$
Schreiben Sie ein Programm, das $q$ berechnet.
Lösung:
Aufgabe 7
Geben Sie sich einige Definitionsbeispiele selbstgewählter Funktionen vor. Achten Sie darauf, dass es sich auch um (echte) partielle Funktionen handeln kann. Außerdem sollten Sie einige abschnittsweise definierte Funktionen, z.B. Briefporto, Zuzahlungen für Medikamente usw., aufnehmen.
Lösung:
Kosten für Infopost
$$q(x)=\begin{cases} (x-20) * 0.352 + 28, & \text{wenn }0 < x \leq 20\text{;}\\ (x-20) * 0.352 + 36, & \text{wenn }20 < x \leq 100\text{;}\\ (x-20) * 0.352 + 73, & \text{wenn }100 < x \leq 1000\text{;}\\ \bot, & \text{sonst.} \end{cases} $$
Aufgabe 8
Wiederholen Sie die folgenden Eigenschaften von Funktionen:
injektiv, surjektiv und bijektiv.
Geben Sie aussagekräftige Beispiele an. Skizzieren Sie folgende Funktionen mittels Abbildungspfeilen aus X in Y : injektiv und surjektiv; injektiv, nicht surjektiv; nicht injektiv, surjektiv; nicht injektiv, nicht surjektiv.
Lösung:
injektiv - Jedes Element aus Y hat höchstens einen Partner in X -- $ \N \Rightarrow \N, x \rightarrow x^2 $
surjektiv - Jedes Element aus Y hat mindestens einen Partner in X -- $ \R \Rightarrow \R_{+}, x \rightarrow x^2 $
bijektiv - Jedes Element aus Y hat genau einen Partner in X (muss injektiv und surjektiv sein) -- $ \R_{+} \Rightarrow \R_{+}, x \rightarrow x^2 $
| Funktion $X \Rightarrow Y$ | Darstellung |
|---|---|
| injektiv,surjektiv | 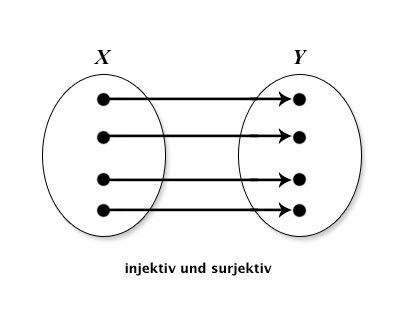
|
| injektiv,nicht surjektiv | 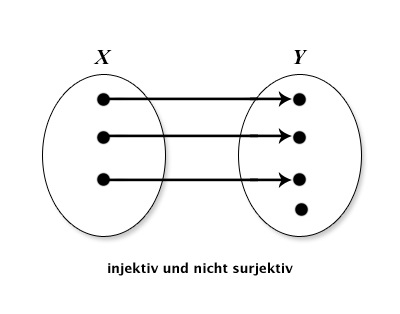
|
| nicht injektiv,surjektiv | 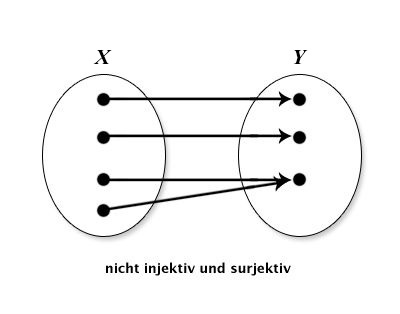
|
| nicht injektiv,nicht surjektiv | 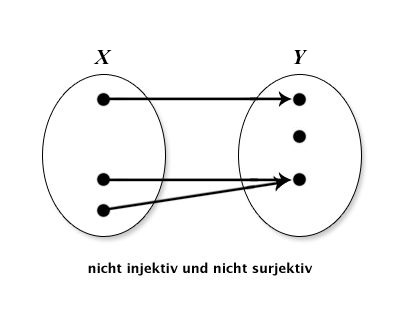
|
Aufgabe 9
Zeigen Sie, dass die Menge $\mathbb{Z}$ eine abzählbar unendliche Menge ist und setzen Sie sich mit der Aussage auseinander, wonach doch $\mathbb{Z}$ eigentlich doppelt so viele Elemente besitzt wie $\mathbb{N}$.
Lösung:
Eine Menge ist dann abzählbar unendlich, wenn eine bijektive Abbildung dieser Menge auf die Menge der natürlichen Zahlen, also ein Durchnumerieren, möglich ist.
| 0 | 1 | 2 | 3 | 4 | 5 | ... | |
| 0 | 1 | -1 | 2 | -2 | 3 | ... |
Beide Mengen sind gleichmächtig, also besitzt $\mathbb{Z}$ genauso viele Elemente wie $\mathbb{N}$
Aufgabe 10
Entwerfen Sie ein Aufbauschema zur systematischen Erzeugung aller Elemente aus $\mathcal{P}(M)$ für eine gegebene endliche Menge M und wenden Sie es auf einige selbstgewählte Beispiele an.
Lösung:
Aufbauschema:
1. Leere Menge aufnehmen
2. Ein Element aus der Menge nehmen, es jedem Element der vorher gebildeten Menge hinzufügen und vorher gebildete Elemente übernehmen
Beispiel
für $ \wp(\{a,b,c\}) $
$ \wp(\{\})=\{\{\emptyset\}\} $
$ \wp(\{a\})=\{\{\emptyset\},\{a\}\} $
$ \wp(\{a,b\})=\{\{\emptyset\},\{a\},\{b\},\{a,b\}\} $
$ \wp(\{a,b,c\})=\{\{\emptyset\},\{a\},\{b\},\{a,b\},\{c\},\{a,c\},\{b,c\},\{a,b,c\}\} $