Thema9

Aus ProgrammingWiki

Aufgabe 1

Weisen Sie nach, dass die AP-Funktion WHILE-berechenbar ist. $$AP(0,\ y) = y+1$$ $$AP(x,\ 0) = AP(x-1,\ 1), x > 0$$ $$AP(x,\ y) = AP(x-1,\ AP(x,\ y-1)), x, y>0$$

Aufgabe 2

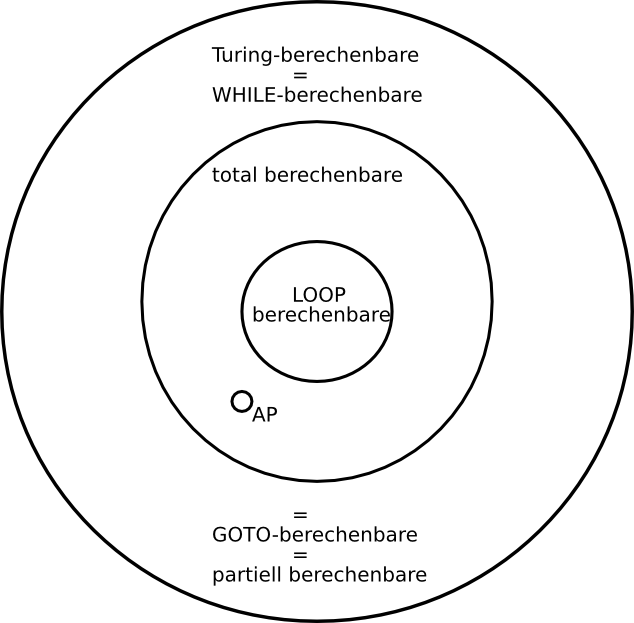
Folgende Klassen sollen dargestellt werden:

• Turing-berechenbare Funktionen
• WHILE-berechenbare Funktionen
• GOTO-berechenbare Funktionen
• partiell berechenbare Funktionen
• total berechenbare Funktionen
• LOOP-berechenbare Funktionen
• AP-Funktion

Kreativaufgabe: LOOP-, WHILE, GOTO-Grammatik

Entwickeln Sie jeweils zu LOOP-, WHILE- und GOTO-Programmen eine entsprechende Grammatik. Überprüfen Sie anhand eines Beispiels ob die von Ihnen entwickelten Grammatiken korrekt sind.

Verwenden Sie AtoCC.

LOOP-Grammatik

$G = (N, T, P, s)$

\begin{eqnarray*} N & = & \{LProgramm,\ LProg,\ Zuweisung,\ Zyklus,\ Sequenz,\ Variable,\ Konstante,\ Operation,\ Zahl,\ Ziffer\}\\ T & = & \{\tt{:=},\ \tt{LOOP},\ \tt{DO},\ \tt{END},\ \tt{;},\ \tt{x},\ \tt{+},\ \tt{-},\ \tt{0},\ \tt{1},\ \tt{2},\ \tt{3},\ \tt{4},\ \tt{5},\ \tt{6},\ \tt{7},\ \tt{8},\ \tt{9}\}\\ P & = & \{ LProgramm \rightarrow LProg\ \\ & & \ \ LProg \rightarrow Zyklus\ \mid\ Sequenz\ \mid\ Zuweisung\ \\ & & \ \ Zuweisung \rightarrow Variable\ \tt{:=}\ Variable\ Operation\ Konstante\ \\ & & \ \ Zyklus \rightarrow \tt{LOOP}\ Variable\ \tt{DO}\ LProg\ \tt{END}\ \\ & & \ \ Sequenz \rightarrow LProg\ \tt{;}\ LProg\ \\ & & \ \ Variable \rightarrow \tt{x}\ Zahl\ \\ & & \ \ Konstante \rightarrow Zahl\ \\ & & \ \ Operation \rightarrow \tt{+}\ \mid\ \tt{-}\ \\ & & \ \ Zahl \rightarrow Ziffer\ \mid\ Ziffer\ Zahl\ \\ & & \ \ Ziffer \rightarrow \tt{0}\ \mid\ \tt{1}\ \mid\ \tt{2}\ \mid\ \tt{3}\ \mid\ \tt{4}\ \mid\ \tt{5}\ \mid\ \tt{6}\ \mid\ \tt{7}\ \mid\ \tt{8}\ \mid\ \tt{9}\ \\ & & \}\\ s & = & LProgramm \end{eqnarray*}