Thema5
Aus ProgrammingWiki
Inhaltsverzeichnis |
Aufgabe 1
Definieren Sie je eine totale Funktion für den Vorgänger und die Halbierung einer natürlichen Zahl. Definieren Sie außerdem eine Funktion mit $D_f = \mathbb{N}\backslash\{1234, 7266281\}$.
Vorgänger $f:\mathbb{N} \rightarrow \mathbb{N}$
$$f(n) = \begin{cases} n-1, & \text{wenn } n \geq 1,\\ 0, & \text{sonst}. \end{cases}$$
Halbierung $f:\mathbb{N} \rightarrow \mathbb{N}$
$$f(n) = \begin{cases} \frac{n}{2}, & \text{wenn n gerade},\\ \frac{n-1}{2}, & \text{sonst}. \end{cases}$$
$D_f = \mathbb{N}\backslash\{1234, 7266281\}$
$$f(n) = \begin{cases} n, & \text{wenn } n \ne 1234,\ n \ne 7266281,\\ \perp, & \text{sonst} \end{cases}$$
Aufgabe 2
Für $K = ((001,0),(01,011),(01,101),(10,001))$ gibt es eine Lösung. Die gesuchte Indexfolge heißt:
$$(2 \ 4 \ 3 \ 4 \ 4 \ 2 \ 1 \ 2 \ 4 \ 3 \ 4 \ 3 \ 4 \ 4 \ 3 \ 4 \ 4 \ 2 \ 1 \ 4 \ 4 \ 2 \ 1 \ 3 \ 4 $$
$$ 1 \ 1 \ 3 \ 4 \ 4 \ 4 \ 2 \ 1 \ 2 \ 1 \ 1 \ 1 \ 3 \ 4 \ 3 \ 4 \ 1 \ 2 \ 1 \ 4 \ 4 \ 2 \ 1 \ 4 \ 1 $$
$$ 1 \ 3 \ 4 \ 1 \ 1 \ 3 \ 1 \ 1 \ 3 \ 1 \ 2 \ 1 \ 4 \ 1 \ 1 \ 3)$$
Überprüfen Sie die angegebene Lösung per Hand.
Lösung für beide:
$$01100110100100101100110011010011010010011010010010110001001011010100100101$$
$$00100100101100110001010011010010011000100101100010010100100101001010011000100101$$
für x:
$$01 \ 10 \ 01 \ 10 \ 10 \ 01 \ 001 \ 01 \ 10 \ 01 \ 10 \ 01 \ 10 \ 10 \ 01 \ 10 \ 10 \ 01 \ 001 \ 10 \ 10 \ 01 \ 001 \ 01 \ 10$$
$$001 \ 001 \ 01 \ 10 \ 10 \ 10 \ 01 \ 001 \ 01 \ 001 \ 001 \ 001 \ 01 \ 10 \ 01 \ 10 \ 001 \ 01 \ 001 \ 10 \ 10 \ 01 \ 001 \ 10 \ 001$$
$$001 \ 01 \ 10 \ 001 \ 001 \ 01 \ 001 \ 001 \ 01 \ 001 \ 01 \ 001 \ 10 \ 001 \ 001 \ 01$$
für y:
$$011 \ 001 \ 101 \ 001 \ 001 \ 011 \ 0 \ 011 \ 001 \ 101 \ 001 \ 101 \ 001 \ 001 \ 101 \ 001 \ 001 \ 011 \ 0 \ 001 \ 001 \ 011 \ 0 \ 101 \ 001$$
$$0 \ 0 \ 101 \ 001 \ 001 \ 001 \ 011 \ 0 \ 011 \ 0 \ 0 \ 0 \ 101 \ 001 \ 101 \ 001 \ 0 \ 011 \ 0 \ 001 \ 001 \ 011 \ 0 \ 001 \ 0$$
$$0 \ 101 \ 001 \ 0 \ 0 \ 101 \ 0 \ 0 \ 101 \ 0 \ 011 \ 0 \ 001 \ 0 \ 0 \ 101$$
Aufgabe 3
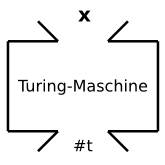
Geben Sie Trichterbilder für den Einsatz einer TM als Akzeptator an:
1. für semi-entscheidbare Sprachen.
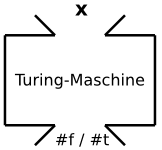
2. für entscheidbare Sprachen.
Aufgabe 4
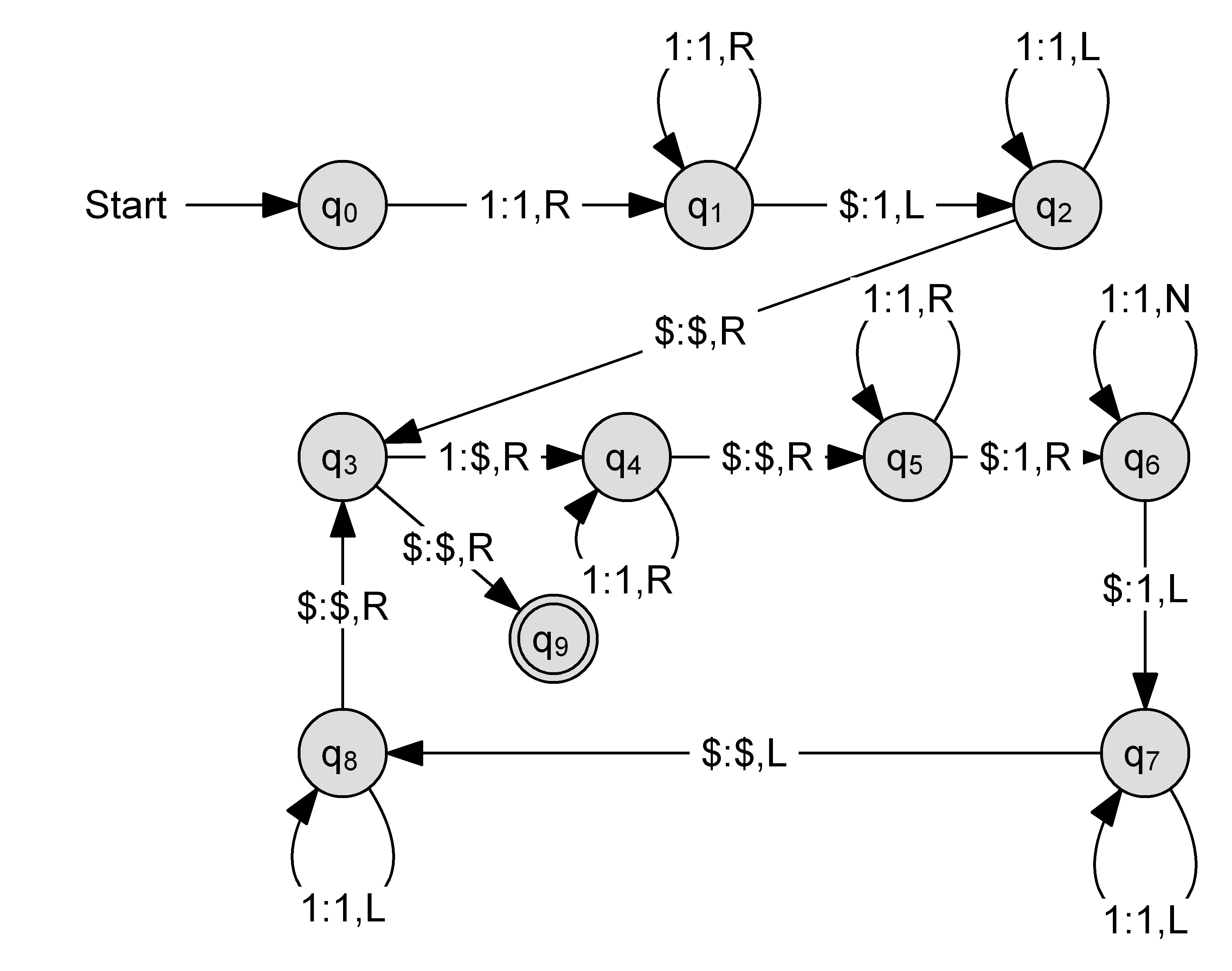
Entwickeln Sie eine Turing-Maschine, welche die konstante Funktion $f(x)=5$ für alle $x\in\mathbb{N}$ berechnet.
Aufgabe 5
Definieren Sie die Begriffe Turing-aufzählbar und Truring-entscheidbar analog zur Turing-Berechenbarkeit
Turing-aufzählbar
Die Menge muss abzählbar und die dazu gehörige Funktion durch eine Turing-Maschine $M$ berechenbar sein.
Turing-entscheidbar
Wenn die $\chi_M$ - Funktion durch eine Turing-Maschine berechenbar ist.
Aufgabe 6
Entwickeln Sie eine Turning-Maschine, welche den Nachfolger einer natürlichen Zahl berechnet.
Kreativaufgabe: RADO-Funktion
$\sum(n)$ bezeichnet die maximale Anzahl von Einsen (nicht unbedingt aufeinander folgend), die eine haltende TM über $\{1\}^*$ und $n$ Zuständen zzgl. eines Haltezustands auf ein anfangs leeres Band schreiben kann. Die Kopfposition am Ende der Berechnung spielt (im Gegensatz zur sonstigen Vereinabrung) keine Rolle.
$\sum:\mathbb{N} \rightarrow \mathbb{N}$ ist eine von Tibor RADO (ungarischer Mathematiker, 1895-1965) angegebene nicht berechenbare Funktion.
z.z.: $\sum$ ist nicht berechenbar.
Methode: Indirekter Beweis
Vorbereitung:
- Beweis der folgenden beiden Eigenschaften der Funktion:
- $\sum(n) < \sum(n+1)$
- Für alle $n$ gilt $f(n) \leq \sum(n+k)$
- Wenn $f$ und $g$ Turing-berechenbare Funktionen sind, dann ist auch $g \circ f$ Turing-berechnbar.
Beweis der 1. Eigenschaft: $\Sigma(n) < \Sigma(n+1)$
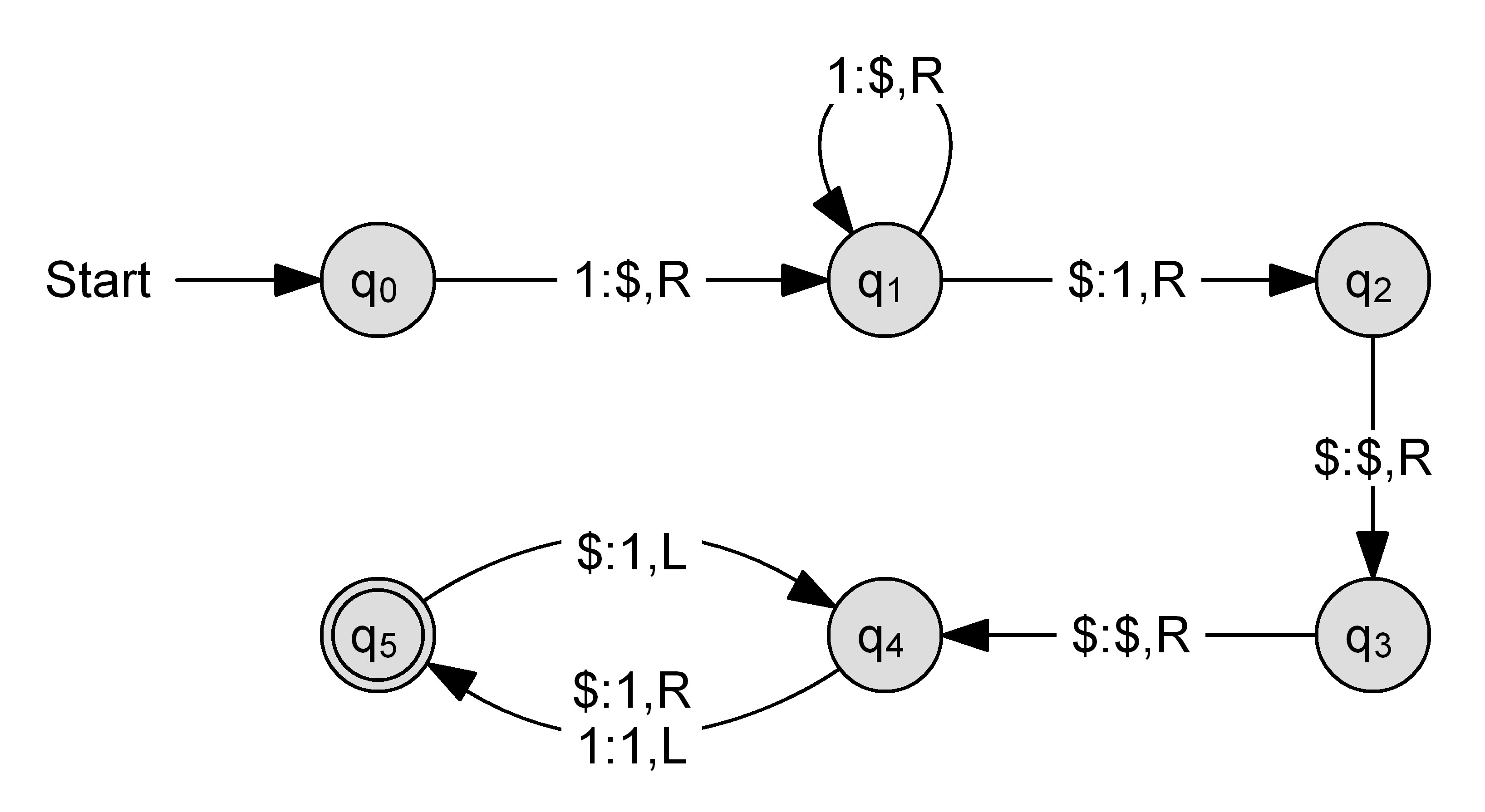
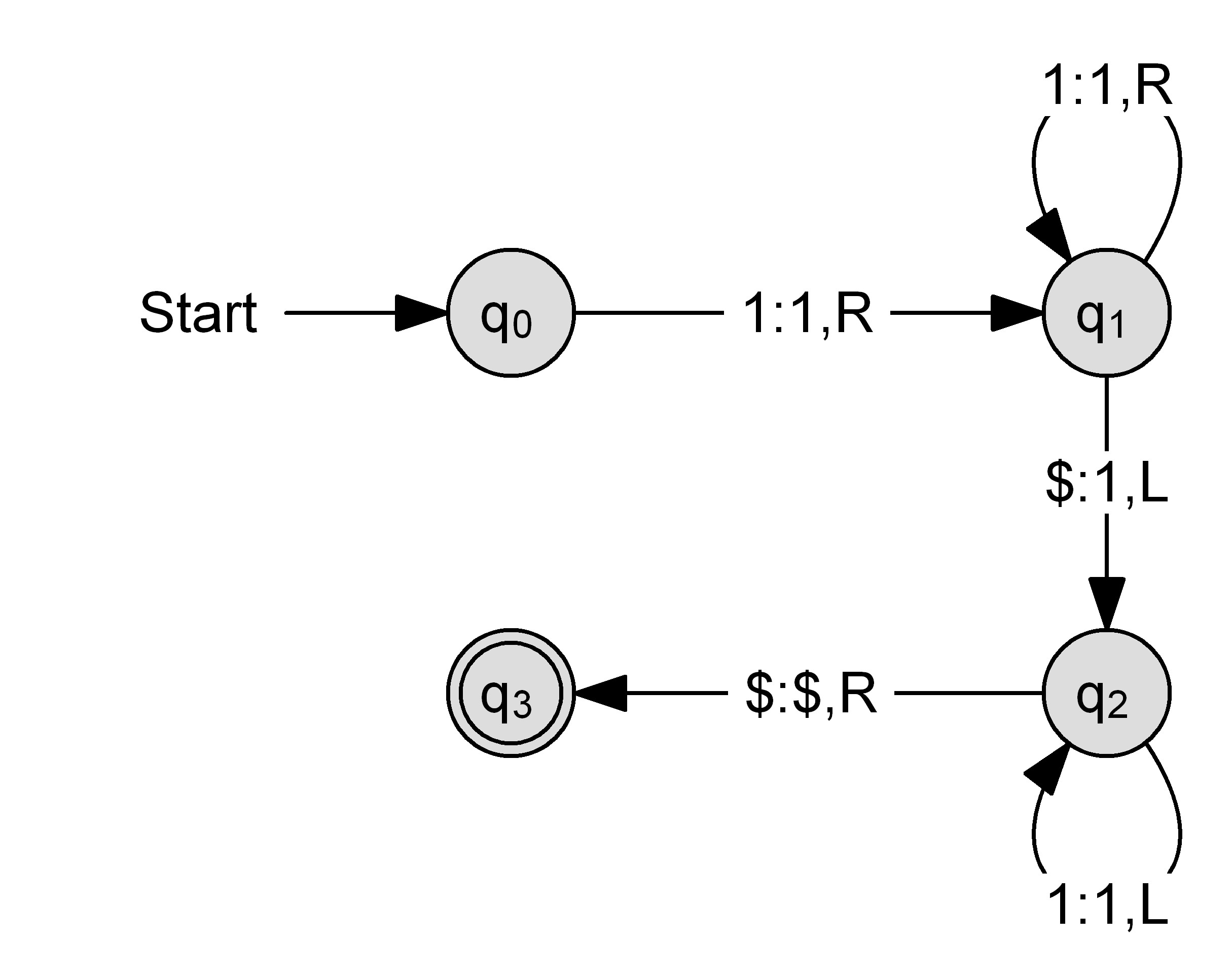
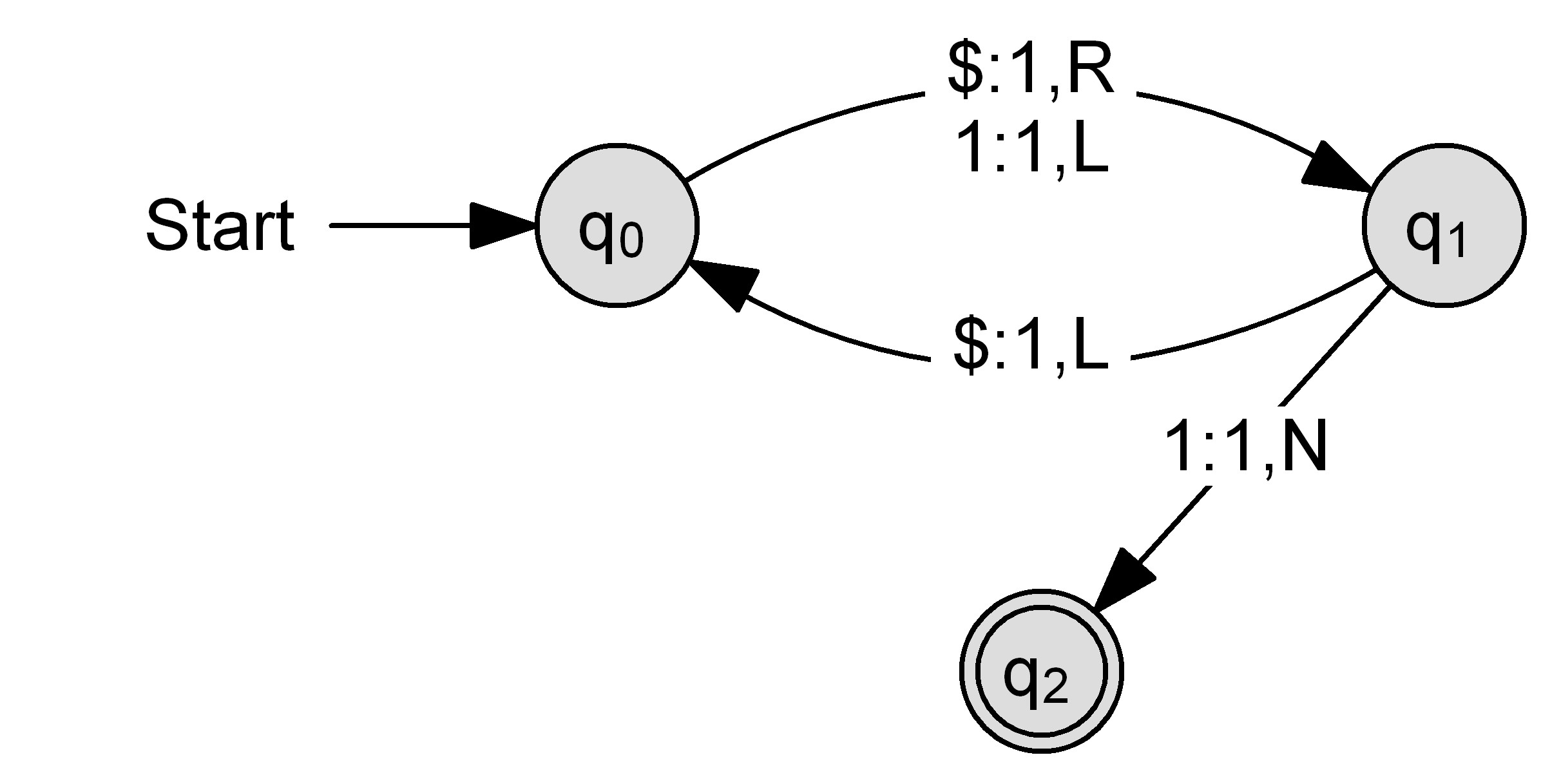
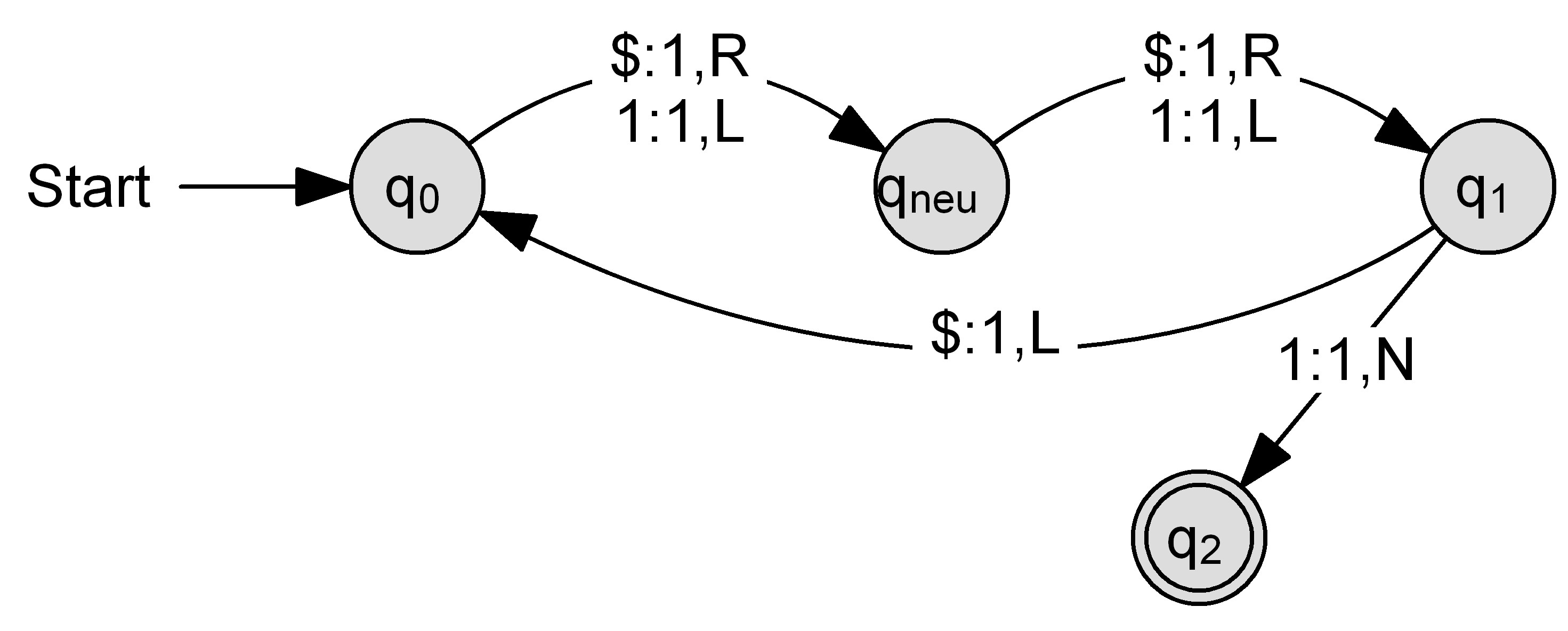
Fügt man einer bestehenden Turing-Maschine zu der RADO-Funktion mit $n$ Zuständen einen weiteren Zustand direkt nach dem Startzustand hinzu, so ist es dieser erweiterten Turing-Maschine möglich, mindestens eine "1" mehr auf das Band zu schreiben. Dies wurde mit folgendem Beispiel für $n=2$ verdeutlicht. Hierbei wird über die Ausgangs-Turing-Maschine viermal "1" auf das Band geschrieben, während bei der um den Zustand $q_{neu}$ erweiterten Turing-Maschine fünfmal "1" geschrieben wird.
Beispiel $n = 2$ und $n = 3$
Ergebnisse:
Beweis der 2. Eigenschaft: Für alle $n$ gilt $f(n) \leq \sum(n+k)$
Die Funktion $f(n)$ wird durch eine Turing-Maschine $M_f$ berechnet. Diese besitzt $k$ Zustände und es können mit ihr zur Berechnung von $f(n)$ $n$ Einsen auf das Band geschrieben werden.
Weiterhin gibt es eine Turing-Maschine zu der RADO-Funktion, die maximal viele Einsen ($x$) bei $k$ Zuständen schreibt. Um mit dieser Turing-Maschine die $n$ Einsen zur Berechnung von $f(n)$ auf das Band zu schreiben, kommen maximal $n$ Zustände zu der bereits bestehenden Maschine hinzu. Die so entstandene Turing-Maschine schreibt also die urspürngliche Anzahl an Einsen $x$ und zusätzlich die $n$ Einsen der Funktion. Somit muss die Anzahl der Einsen von $\sum(n+k)$ mindestens $n$ betragen.
Beweis der 3. Eigenschaft: Wenn $f$ und $g$ Turing-berechenbare Funktionen sind, dann ist auch $g \circ f$ Turing-berechnbar.
Da $f$ und $g$ Turing-berechenbar sind, existieren für beide Funktionen Turing-Maschinen. Die Verkettung dieser beiden Funktionen kann über die Kopplung der zugehörigen Maschinen realisiert werden, sodass wieder eine Turing-berechenbare Funktion entsteht.
Beispiel:
$f$ stellt die Turing-Maschine zur Berechnung des Nachfolgers einer natürlichen Zahl dar.
$g$ stellt die Turing-Maschine zur Verdopplung einer natürlichen Zahl dar.
Beweis: $\sum$ ist nicht berechenbar
Methode: indirekter Beweis $\rightarrow$ $\sum$ ist berechenbar
Da $\sum$ berechenbar ist, existiert eine Turing-Maschine zu dieser Funktion. Weitherin ist die Verdopplung einer natürlichen Zahl (V) berechenbar, sodass auch hier eine Turing-Maschine existiert. Nach Eigenschaft 3 muss die Verkettung zweier Turing-berechenbarer Funktionen ebenfalls Turing-berechenbar sein. Daraus ergibt sich:
$\Sigma \circ V$ ist Turing-berechenbar, sodass eine Turing-Maschine $M_{\Sigma \circ V}$ mit $k$ Zuständen existiert. $\Sigma \circ V$ stellt dabei eine Funktion $f$ dar.
Nach Eigenschaft 2 gilt für alle $n \in \mathbb{N}$ $f(n) \leq \sum(n+k)$. $f$ wird hierbei mit $(\Sigma \circ V)$ ersetzt:
$$(\Sigma \circ V) \leq \Sigma(n+k)$$
wobei $\Sigma \circ V$ auch als $\Sigma(V(n))$ dargestellt werden kann. Die Verdopplungsfunktion ist hierbei durch $g(n) = 2n$ definiert. Daraus ergibt sich:
$$\Sigma(2n) \leq \Sigma(n+k)$$
Für ein spezielles $n = k + 1$ folgt folgende Gleichung:
$$\Sigma(2(k+1)) \leq \Sigma((k+1) + k)$$
$$\Sigma(2k+2) \leq \Sigma(2k+1) \unicode{x021AF}\text{ Widerspruch!}$$
Der Widerspruch entsteht durch Eigenschaft 1, laut der $\sum(n) < \sum(n+1)$ gilt. Dies ist nicht gegeben, da sich $\sum(2k+2) > \sum(2k+1)$ ergeben hat.
Somit ist bewiesen worden, dass die RADO-Funktion nicht berechenbar ist.