Thema1
Aus ProgrammingWiki
Inhaltsverzeichnis |
Aufgabe 01
Beweisen Sie indirekt, dass $x$ eine gerade Zahl ist, wenn $x^2$ mit $x \in \mathbb{N}$ eine gerade Zahl ist.
Wenn $x^2$ eine gerade Zahl ist, dann ist x ebenfalls eine gerade Zahl.
Annahme: x ist eine ungerade Zahl $\rightarrow$ Wenn 2|$x^2$ dann 2|x.
$ Y = x^2$ ist gerade; $\overline{Y} = x^2$ ist ungerade
$x = 2k + 1 \text{ mit } k \in \mathbb{N}$ $x^2 = 4k^2 + 4k + 1 = 2j$ $x^2 = 2\underbrace{(2k + 2)}_{j} + 1$
Aus +1 folgt, dass $x^2$ nicht gerade ist, wodurch ein Widerspruch entsteht, da gilt, dass $x^2$ gerade ist.
Daraus folgt, dass x gerade ist.
Aufgabe 02 + 03
Beweisen Sie die Aussage, wonach aus der Gültigkeit der Aussagen $A \Rightarrow B, B \Rightarrow C$ und $\overline{C}$ die Gültigkeiten von $\overline{A}$ und $\overline{B}$ folgen. Stellen Sie den Sachverhalt in einer Wahrheitstabelle dar.
Was kann man über die Gültigkeit von $A$ und $B$ schließen, wenn bekannt ist, dass $A \Rightarrow B, B \Rightarrow C$ und $C$ gelten?
| $A$ | $B$ | $C$ | $\overline{A}$ | $\overline{B}$ | $\overline{C}$ | $A \Rightarrow B$ | $B \Rightarrow C$ | $A \Rightarrow B, B \Rightarrow C, \overline{C}$ | $A \Rightarrow B, B \Rightarrow C, C$ |
|---|---|---|---|---|---|---|---|---|---|
| $$0$$ | $$0$$ | $$0$$ | $$1$$ | $$1$$ | $$1$$ | $$1$$ | $$1$$ | $$1$$ | $$0$$ |
| $$0$$ | $$0$$ | $$1$$ | $$1$$ | $$1$$ | $$0$$ | $$1$$ | $$1$$ | $$0$$ | $$1$$ |
| $$0$$ | $$1$$ | $$0$$ | $$1$$ | $$0$$ | $$1$$ | $$1$$ | $$0$$ | $$0$$ | $$0$$ |
| $$0$$ | $$1$$ | $$1$$ | $$1$$ | $$0$$ | $$0$$ | $$1$$ | $$1$$ | $$0$$ | $$1$$ |
| $$1$$ | $$0$$ | $$0$$ | $$0$$ | $$1$$ | $$1$$ | $$0$$ | $$1$$ | $$0$$ | $$0$$ |
| $$1$$ | $$0$$ | $$1$$ | $$0$$ | $$1$$ | $$0$$ | $$0$$ | $$1$$ | $$0$$ | $$0$$ |
| $$1$$ | $$1$$ | $$0$$ | $$0$$ | $$0$$ | $$1$$ | $$1$$ | $$0$$ | $$0$$ | $$0$$ |
| $$1$$ | $$1$$ | $$1$$ | $$0$$ | $$0$$ | $$0$$ | $$1$$ | $$1$$ | $$0$$ | $$1$$ |
Wenn $A \Rightarrow B, B \Rightarrow C$ und $C$ gelten, dann
- gelten $A$ und $\overline{B}$, oder
- gelten $\overline{A}$ und B, oder
- gelten sowohl $A$, als auch $B$
Aufgabe 04
Beweisen Sie die von Jacques P. M. Binet (1786-1856) im Jahre 1843 $F_n = \frac {1}{\sqrt{5}}((\frac{1+\sqrt{5}}{2})^n - (\frac{1-\sqrt{5}}{2})^n)$ für die Fibonacci-Zahlenfolge:
$F_0 = 0$
$F_1 = 1$
$F_n = F_{n-1} + F_{n-2}$, mit $n \geq 2$
mit vollständiger Induktion.
Induktionsanfang:
i = 0
$F_0 = 0$
$F_0 = \frac{1}{\sqrt{5}}((\frac{1+\sqrt{5}}{2}^0 - (\frac{1-\sqrt{5}}{2})^0)$
$F_0 = \frac{1}{\sqrt{5}}(1-1) = 0$
und
i = 1
$F_1 = 1$
$F_1 = \frac{1}{\sqrt{5}}((\frac{1+\sqrt{5}}{2}^1 - (\frac{1-\sqrt{5}}{2})^1)$
$F_1 = \frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}-1+\sqrt{5}}{2})$
$F_1 = \frac{1}{\sqrt{5}}(\frac{2-\sqrt{5}}{2}) = 1$
Induktionsschritt:
Wenn $F_n = \frac {1}{\sqrt{5}}((\frac{1+\sqrt{5}}{2})^n - (\frac{1-\sqrt{5}}{2})^n)$ (Induktionsvoraussetzung), dann $F_{n+1} = \frac {1}{\sqrt{5}}((\frac{1+\sqrt{5}}{2})^{n+1} - (\frac{1-\sqrt{5}}{2})^{n+1})$
Induktionsbeweis:
$F_{n+1} = F_n + F_{n-1}$
$F_{n+1} = F_n + \frac {1}{\sqrt{5}}((\frac{1+\sqrt{5}}{2})^{n-1} - (\frac{1-\sqrt{5}}{2})^{n-1})$
$F_{n+1} = F_n + \frac{1}{\sqrt{5}}\left(\cfrac{(\frac{1+\sqrt{5}}{2})^n}{\frac{1+\sqrt{5}}{2}} - \cfrac{(\frac{1-\sqrt{5}}{2})^n}{\frac{1-\sqrt{5}}{2}} \right)$
$F_{n+1} = F_n + \frac{1}{\sqrt{5}}\cfrac{(\frac{1+\sqrt{5}}{2})^n(\frac{1-\sqrt{5}}{2}) - (\frac{1-\sqrt{5}}{2})^n(\frac{1+\sqrt{5}}{2})}{-1} $
$F_{n+1} = \frac{1}{\sqrt{5}}\left((\frac{1+\sqrt{5}}{2})^n - (\frac{1-\sqrt{5}}{2})^n\right) - \frac{1}{\sqrt{5}}\left((\frac{1+\sqrt{5}}{2})^n(\frac{1-\sqrt{5}}{2}) - (\frac{1-\sqrt{5}}{2})^n(\frac{1+\sqrt{5}}{2})\right)$
$F_{n+1} = \frac{1}{\sqrt{5}} \left((\frac{1+\sqrt{5}}{2})^n(1-(\frac{1-\sqrt{5}}{2})) - (\frac{1-\sqrt{5}}{2})^n(1-(\frac{1+\sqrt{5}}{2}))\right)$
$F_{n+1} = \frac{1}{\sqrt{5}}\left((\frac{1+\sqrt{5}}{2})^n(\frac{1+\sqrt{5}}{2}) - (\frac{1-\sqrt{5}}{2})^n(\frac{1-\sqrt{5}}{2})\right)$
Aufgabe 05
Beweisen Sie die folgenden Beziehungen für Fibonacci-Zahlen mit $n \in \mathbb{N}$ und $n \geq 1$ nach Definition im Beispiel mittels vollständiger Induktion:
- $\sum_{k=1}^n F_k = F_{n+2} - 1$
- $\sum_{k=1}^n F_{2k} = F_{2n+1} - 1$
- $\sum_{k=1}^n F_{2k-1} = F_{2n}$
1.)
Induktionsanfang n = 1:
$\sum_{k=1}^1 F_k = F_{1+2} - 1$
$F_1 = F_3 - 1$
$1 = F_2 + F_1 - 1 = F_1 + F_0 + F_1 - 1$
$1 = 1$
Induktionsschritt:
Wenn $\sum_{k=1}^n F_k = F_{n+2} - 1$ (IV), dann $\sum_{k=1}^{n+1} F_k = F_{n+3} - 1$
Induktionsbeweis:
$\sum_{k=1}^{n+1} F_k = \sum_{k=1}^n F_k + F_{n+1}$
$= F_{n+2} - 1 + F_{n+1}$ (IV)
$ = F_{n+2} + F_{n+1} - 1$
$ = F_{n+3} - 1$ (Def.)
2.)
Induktionsanfang n = 1:
$\sum_{k=1}^n F_{2k} = F_{2n+1} - 1$
$F_2 = F_3 -1$
$1 = 2-1$
$1 = 1$
Induktionsschritt:
Wenn $\sum_{k=1}^n F_{2k} = F_{2n+1} - 1$ (IV), dann $\sum_{k=1}^{n+1} F_{2k} = F_{2n+3} - 1$
Induktionsbeweis:
$\sum_{k=1}^{n+1} F_{2k} = \sum_{k=1}^n F_{2k} + F_{2(n+1)}$
$ = F_{2n+1} - 1 + F_{2n+2}$ (IV)
$ = F_{2n+3} - 1$ (Def.)
3.)
Induktionsanfang n = 1:
$\sum_{k=1}^1 F_{2-1} = F_{2}$
$F_1 = F_2$
$1 = 1$
Induktionsschritt:
Wenn $\sum_{k=1}^n F_{2k-1} = F_{2n}$ (IV), dann $\sum_{k=1}^{n+1} F_{2k-1} = F_{2n+2}$
Induktionsbeweis:
$\sum_{k=1}^{n+1} F_{2k-1} = \sum_{k=1}^n F_{2k-1} + F_{2n+1}$
$ = F_{2n} + F_{2n+1}$ (IV)
$ = F_{2n+2}$ (Def.)
Aufgabe 06
Wiederholen Sie die Eigenschaften von Äquivalenzrelationen und gebe Sie ein Beispiel an.
Eine Äquivalenzrelation ist eine Relation, die reflexiv, transitiv und symmetrisch ist.
- reflexiv = jedes Objekt ist zu sich selbst äquivalent
- transitiv = Wenn a zu b äquivalent ist, dann ist auch b zu a äquivalent
- symmetrisch = Wenn a zu b und b zu c äquivalent ist, dann ist auch a äquivalent zu c
Beispiel: Bücher und ihre ISB-Nummer
- für jedes Buch x gilt, dass x und x dieselbe ISBN besitzen
- Wenn x und y dieselbe ISBN haben, dann haben auch y und x dieselbe ISBN
- Wenn x und y dieselbe ISBN haben und auch y und z, dann haben x und z auch dieselbe ISBN
Eine Ordnungsrelation ist eine Relation, welche die Kleiner-Gleich-Relation ($\leq$) verallgemeinert. Das heißt, die Elemente einer Menge können der Größe nach geordnet und verglichen werden.
Aufgabe 07
Schreiben Sie ein Programm, das q berechnet.
$$q(x) = \begin{cases} \frac{35}{x-3}, & \text{wenn } x \ne 3, \\ \perp, & \text{sonst}. \end{cases}$$
Aufgabe 08
Geben Sie sich einige Definitionsbeispiele selbstgewählter Funktionen vor. Achten Sie darauf, dass es sich auch um (echte) partielle Funktionen handeln kann. Außerdem sollten Sie einige abschnittsweise definierte Funktionen, z.B. Briefporto, Zuzahlung für Medikamente, etc., aufnehmen.
$f(x) = 3x+5$
$f(x) = 3x^2 + 7x - 2$
$f(x) = \begin{cases} \frac{1}{x-1} + \frac{1}{x-2}, & \text{wenn } x \ne 1 \text{ und } x \ne 2,\\ \perp & \text{sonst}. \end{cases}$
Briefporto: $f(x)=\begin{cases} 0.75, & \text{ wenn } x \leq 20\text{,}\\ 1.50, & \text{ wenn } 20 < x \leq 50\text{,}\\ 3.45, & \text{ wenn } 50 < x \leq 500\text{,}\\ 7.00, & \text{ wenn } 500 < x \leq 1000\text{,}\\ 16.90, & \text{ wenn } 1000 < x \leq 2000\text{,}\\ \bot, & \text{ sonst} \end{cases}$
Aufgabe 09
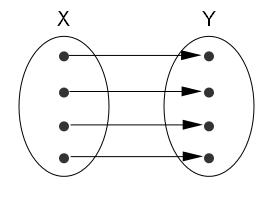
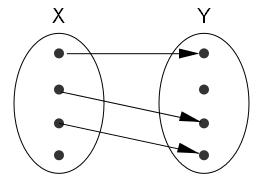
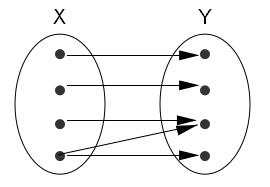
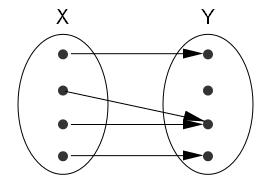
Wiederholen Sie die folgenden Eigenschaften von Funktionen: injektiv, surjektiv, bijektiv. Geben Sie aussagekräftige Beispiele an. Skizzieren Sie folgende Funktionen mittels Abbildungspfeilen aus X und Y:
- injektiv und surjektiv
- injektiv und nicht surjektiv
- nicht injektiv und surjektiv
- nicht injektiv und nicht surjektiv
injektiv (linkstotal): eine Funktion ist injektiv, wenn jeder y-Wert nur maximal einen dazugehörigen x-Wert besitzt
surjektiv (rechtstotal): eine Funktion ist surjektiv, wenn jeder mögliche y-Wert in der Zielmenge angenommen wird
bijektiv (links- und rechtstotal): für jedes x aus X existiert genau ein y aus Y.
injektiv und surjektiv
injektiv und nicht surjektiv
nicht injektiv und surjektiv
nicht injektiv und nicht surjektiv
Aufgabe 10
Zeigen Sie, dass die Menge $\mathbb{Z}$ eine abzählbar unendliche Menge ist und setzen Sie sich mit der Aussage auseinander, wonach doch $\mathbb{Z}$ eigentlich doppelt so viele Elemente besitzt wie $\mathbb{N}$.
Die Idee ist, den geraden natürlichen Zahlen die negativen Werte und den ungeraden natürlichen Zahlen die positiven Werte der ganzen Zahlen zuzuordnen:
$$f(i) = \begin{cases} -\frac{i}{2}, & \text{wenn i = gerade}\\ \frac{i+1}{2}, & \text{sonst}.\end{cases}$$
Durch diese Funktion kann jede natürliche Zahl auf eine ganze Zahl bijektiv abgebildet werden. Somit sind diese beiden Mengen gleichmächtig und enthalten daher gleich viele Elemente.
Aufgabe 11
Entwerfen Sie ein Aufbauschema zu systematischen Erzeugung aller Elemente aus $\wp(M)$ einer gegebene endliche Menge $M$ und wenden Sie es auf einige selbstgewählte Beispiele an.
- Leere Menge aufnehmen
- Erstes Element der Menge $M$ nehmen und mit allen bereits vorhandenen Elementen der Potenzmenge $\wp(M)$ kombinieren
- Mit den restlichen Elementen von $M$ nach Punkt 2 verfahren
Beispiel
für $ \wp(\{a,b,c\}) $
$ \wp(\{\})=\{\{\emptyset\}\} $
$ \wp(\{a\})=\{\{\emptyset\},\{a\}\} $
$ \wp(\{a,b\})=\{\{\emptyset\},\{a\},\{b\},\{a,b\}\} $
$ \wp(\{a,b,c\})=\{\{\emptyset\},\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\}\} $