s3erjaeh
Aus ProgrammingWiki

Inhaltsverzeichnis |
BuK-KA-Zeitbeschränkte-Prozesse
Aufgabenstellung
Implementieren Sie die im Beweis definierte Aufzählfunktion für $M \subseteq \text{ A*}$ unter Verwendung der Cantorschen Paarungsfunktion. Wählen Sie im Fallbeispiel A = $\{a,b,c\}, g: \N \mapsto A^*$ und M = $\{w |w \in A^* \text{ und } w \text{ enthält Fibonacci-zahlig viele} "b's"\}$.
Machen Sie bei der Konstruktion von $\chi^'_M$ nur von der Semi-Entscheidbarkeit der Menge der Fibonacci-Zahlen Gebrauch, obwohl doch deren Entscheidbarkeit durch Beschränkung des Suchraumes gegeben ist.
Hinweis: Sie benötigen keine engines. Das einfache Timer-System reicht aus. Um Prozesse, die in eine bestimmten Vorgabezeit nicht terminieren, auch wirklich abbrechen zu können, benötigen Sie Continuations (Sprachelement call/cc).
Schritt 1
Implementieren Sie die im Beweis definierte Aufzählfunktion für $M \subseteq \text{ A*}$ unter Verwendung der Cantorschen Paarungsfunktion.
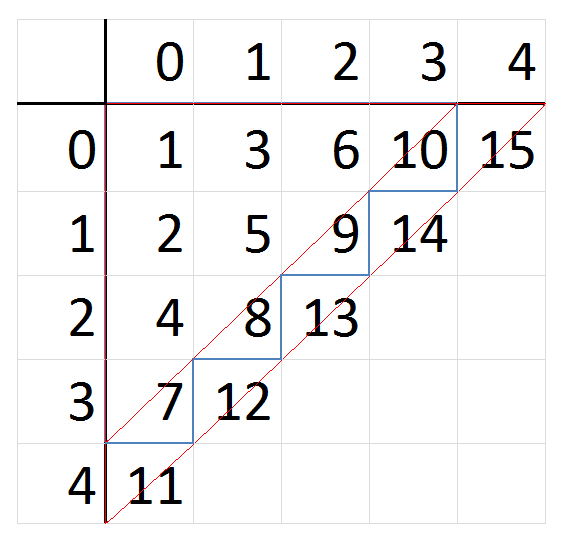
Definition der Cantorschen Paarungsfunktion
$$\begin{array}{c|cccccc}
n\backslash t & 0 & 1 & 2 & 3 & 4 & \dots\\\hline
0 & 0 & 2 & 5 & 9 & 14 & \dots \\
1 & 1 & 4 & 8 & 13 & \dots & \\
2 & 3 & 7 & 12 & \dots & & \\
3 & 6 & 11 & \dots & & & \\
4 & 10 & \vdots & \vdots & \vdots & \vdots &
\end{array}$$
$n$ bestimmt das $n$-te Element, also $g(n)=w_n$, in der Aufzählung von $A^*$ durch $g$. Und $t$ bestimmt die zur Berechnung von $\chi^'_M(w_n)$ bereitgestellten Zeiteinheiten (Takte, ticks) - entweder für die Berechnung ausreichend oder Abbruch nach Zeit t.
$$
z = \pi(n,t) = \frac{(n+t)(n+t+1)}{2} + t
$$
Um die beiden natürlichen Zahlen $n$ und $t$ aus $z$ zu gewinnen, wird die Umkehrfunktion benötigt. Dazu gibt es folgende Überlegung:
Die fortlaufende Zahl z kann als Zählung von Flächenquadraten in einem Dreieck angesehen werden. Somit kann über die Berechnung der Dreiecksfläche $A=\frac{a^2}{2}$ die Seitenlänge ermittelt werden. Würde man nun 10 solcher Flächenquadrate zählen (blau), wäre diese Fläche größer als das rote kleine Dreick mit einer Seitenlänge von 4 und kleiner als das rote große Dreieck mit einer Seitenlänge von 5. Liegt die errechnete Seitenlänge nun unter 4,5 handelt es sich um ein Dreieck mit der Seitenlänge 4. Ist die Seitenlänge größer als 4,5 besitzt das Dreieck eine Seitenlänge von 5. Um dies zu vereinfachen kann zu der errechneten Seitenlänge 0,5 addiert werden. Der Abgerundete Wert der errechneten Seitenlänge enspricht nun genau der größtmöglichen $n$ bzw. $t$ Koordinate in dem jeweiligen Dreieck.
$$ A=\frac{a^2}{2} $$ $$a=\sqrt{A*2}$$ $$a=\lfloor\sqrt{A*2}+0,5\rfloor$$ $$f(z)=\lfloor\sqrt{z*2}+0,5\rfloor$$
Ist die Seitenlänge bekannt, kann die Anzahl an Flächenquadraten für das ganze Dreieck errechnet werden. Dazu kann die Cantorschen Paarungsfunktion genutzt werden und mit $t=0$ vereinfacht werden, da bei $t=0$ sich die größten Werte von $z$ befinden. Durch subtraktion des ermittelten Flächenmaxima mit der gegebenen Fläche $z$ kann $n$ errechnet werden. Die Differenz von der Seitenlänge und $n$ entspricht nun $t$. Für die Korrektur des Indexes aufgrund der 0-Basis von $t$ wird zusätzlich 1 subtrahiert.
$$\pi(n,t)=\frac{(n+t)(n+t+1)}{2}+t$$ $$\textrm{mit } t=0 \textrm{ :}$$ $$\pi(n)=\frac{(n)(n+1)}{2}$$
$$n(z) = \pi(f(z)) - z$$ $$t(z) = f(z) - n(z) - 1$$
Da im Model aufgrund der einfacheren Herleitung von 1 angefangen wird zu zählen, müssen wir in der Funktion alle Werte von $z$ mit $z+1$ ersetzen. Daraus ergiebt sich folgende Scheme Prozedur: