uebung1

Aus ProgrammingWiki

Inhaltsverzeichnis 1 Eigenschaften von Funktionen 2 Beispiele 3 Potenzmenge 3.1 Beispiel 3.2 Funktion 4 Aufgabe 2 und 3 4.1 Aufgabe 2 4.2 Aufgabe 3 5 Relation

Eigenschaften von Funktionen

Eigenschaft	Beschreibung	Formel Beispiele
surjektiv	Jedes Element aus B hat mindestens einen Partner in A	$ \R \Rightarrow \R_{+}, x \rightarrow x^2 $
nicht surjektiv		$ \R \Rightarrow \R, x \rightarrow x^2 $, da z.B. -1 keinen zugehörigen x Wert besitzt
injektiv	Jedes Element aus B hat höchstens einen Partner in A	$ \N \Rightarrow \N, x \rightarrow x^2 $
nicht injektiv		$ \Z \Rightarrow \Z, x \rightarrow x^2 $, da -1 und 1 das selbe Ergebnis besitzen.
bijektiv	Jedes Element aus B hat genau einen Partner in A (muss injektiv und surjektiv sein)	$ \R_{+} \Rightarrow \R_{+}, x \rightarrow x^2 $
nicht bijektiv		$ \R \Rightarrow \R_{+}, x \rightarrow x^2 $

Beispiele

Funktion $X \Rightarrow Y$	Darstellung
injektiv,surjektiv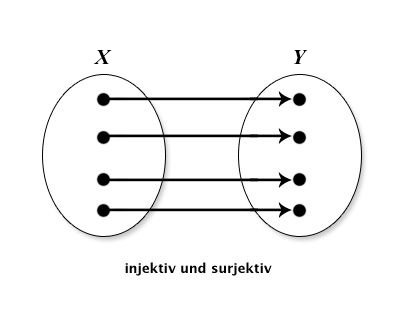
injektiv,nicht surjektiv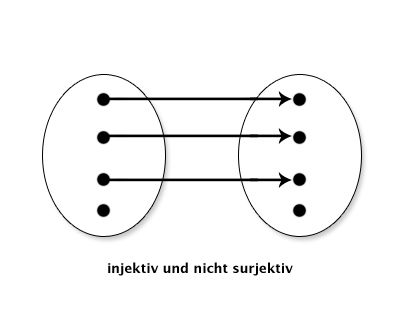
nicht injektiv,surjektiv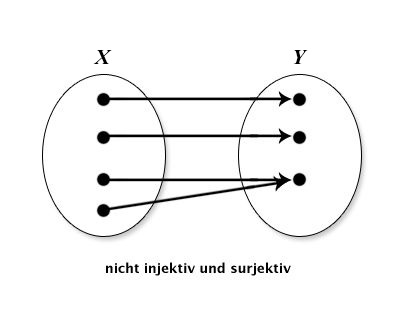
nicht injektiv,nicht surjektiv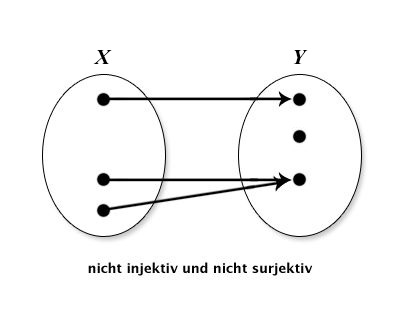

Potenzmenge

Ist die Menge aller Teilmengen. $ P(X) = \{U | U \subset X\} $Sie besitzt $2^n$ Elemente.

1. Leere Menge aufnehmen
2. Mengen mit 1 Element aufnehmen
3. Mengen mit 2 Elementen aufnehmen
   1. 1. Element mit 2.
   2. 1. Element mit 3.
   3. ...
   4. 1. Element mit n.
   5. 2. Element mit 3.
   6. ...
   7. n-1. Element mit n.
4. ...
5. n Stellige Menge aufnehmen

Beispiel

$ P(\{a,b,c\})=\{\{\emptyset\},$
$ P(\{a,b,c\})=\{\{\emptyset\},\{a\},\{b\},\{c\},$
$ P(\{a,b,c\})=\{\{\emptyset\},\{a\},\{b\},\{c\}\},\{ab\},\{ac\},\{bc\},$
$ P(\{a,b,c\})=\{\{\emptyset\},\{a\},\{b\},\{c\}\},\{ab\},\{ac\},\{bc\},\{abc\}\} $

Funktion

(define (haenge-an liste1 liste2) (cond ((and (null? liste1)(null? liste2)) '()) ((not (null? liste1)) (cons (car liste1) (haenge-an (cdr liste1) liste2))) ((not (null? liste2)) (cons (car liste2) (haenge-an liste1 (cdr liste2))))))

(define potenzmenge (lambda (ls) (if (null? ls) '(()) (let ([pm-alt (potenzmenge (cdr ls))]) (haenge-an pm-alt (map (lambda(x) (cons (car ls) x)) pm-alt))))))

(potenzmenge '(a b c))

ausführen

Aufgabe 2 und 3

Zeile	$A$	$B$	$C$	$\overline{A}$	$\overline{B}$	$\overline{C}$	$A \Rightarrow B$	$B \Rightarrow C$
1	W	W	W	F	F	F	W	W
2	W	W	F	F	F	W	W	F
3	W	F	W	F	W	F	F	W
4	W	F	F	F	W	W	F	W
5	F	W	W	W	F	F	W	W
6	F	W	F	W	F	W	W	F
7	F	F	W	W	W	F	W	W
8	F	F	F	W	W	W	W	W

Aufgabe 2

Beweisen Sie die Aussage, wonach aus der Gültigkeit der Aussagen $A \Rightarrow B$, $B \Rightarrow C$ und $\overline{C}$ die Gültigkeiten von $\overline{A}$ und $\overline{B}$ folgen. Stellen Sie den Sachverhalt in einer Wahrheitstabelle dar.

Lösung: Laut der Spalten $\overline{C}, A \Rightarrow B, B \Rightarrow C$ werden diese nur in Zeile 8 Wahr

Zeile	$\overline{A}$	$\overline{B}$	$\overline{C}$	$A \Rightarrow B$	$B \Rightarrow C$
8	W	W	W	W	W

Aufgabe 3

Was kann man über die Gültigkeit von A und B schließen, wenn bekannt ist, dass $A \Rightarrow B$, $B \Rightarrow C$ und $C$ gelten? Verwenden Sie die Tabelle aus der vorhergehenden Aufgabenlösung.

Lösung: Laut Spalten $C, A \Rightarrow B , B \Rightarrow C$ werden diese in Zeile 1,5,7 Wahr woraus folgt:

Zeile	$A$	$B$	$C$	$A \Rightarrow B$	$B \Rightarrow C$
1	W	W	W	W	W
5	F	W	W	W	W
7	F	F	W	W	W

Relation

Wiederholen Sie die Eigenschaften von Äquivalenzrelationen und geben Sie ein Beispiel an.

Relation

Wiederholen Sie die Eigenschaften von Äquivalenzrelationen und geben Sie ein Beispiel an.

Gleichheit gewisser Eigenschaften definiert werden kann, eine Äquivalenzrelation.

• Reflexivität: $a\sim a$
  • Jedes Objekt ist zu sich selbst äquivalent.
• Symmetrie: $a\sim b \ \Rightarrow\ b\sim a$
  • Wenn a zu b äquivalent ist, dann ist auch b äquivalent zu a (und umgekehrt).
• Transitivität: $a\sim b\ \mathrm{und}\ b\sim c\ \Rightarrow\ a\sim c$
  • Wenn a zu b äquivalent und b zu c äquivalent ist, dann ist a äquivalent zu c.