sirokrau

Aus ProgrammingWiki

Inhaltsverzeichnis 1 Übung 2 1.1 Aufgabe 1 2 Übung 3 2.1 Aufzählbarkeit und Entscheidbarkeit (Aufgabe 5) 3 Übung 4 3.1 Teilaufgabe 2 - Beweis Teil 2 (Tobias Salzmann, Ronald Krause) 3.1.1 Beweis 4 RAM-Programm: (Tobias Salzmann und Ronald Krause) 4.1 Ganzzahlige Division 4.2 Größer/Kleinervergleich

Übung 2

Aufgabe 1

$$ \sum\limits_{k=1}^{n} F_{k} = F_{n+2} - 1$$

Induktionsanfang (IA):

z.z. Für n = 1 gilt:

$F_{1}$ = $F_{1+2}-1$

$F_{1}$ = $F_{3}-1$ ($F_{3}$ = 2)

1 = 2-1

1 = 1 $\Rightarrow$ OK

Induktionsschritt (IS):

Wenn $ \sum\limits_{k=1}^{i} F_{k} = F_{i+2} - 1$ (Induktionsvoraussetzung, kurz IV),

dann gilt auch: $ \sum\limits_{k=1}^{i+1} F_{k} = F_{i+3} - 1$ (Induktionsbehauptung, kurz IB).

$ \sum\limits_{k=1}^{i+1} F_{k} = \sum\limits_{k=1}^{i} F_{k} + F_{i+1}$ $\quad \stackrel{IV}{=}$ $ F_{i+2} -1 + F_{i+1}$ $ = F_{i+3} - 1$ (Ergebnis = IB)

Übung 3

Aufzählbarkeit und Entscheidbarkeit (Aufgabe 5)

(define stream-car car) (define stream-cdr (lambda (s) (force (cdr s)))) (define-syntax stream-cons (syntax-rules () ((_ head tail) (cons head (delay tail))))) (define stream-map (lambda (f s) (stream-cons (f (stream-car s)) (stream-map f (stream-cdr s))))) (define nat-stream (lambda (start) (stream-cons start (nat-stream (+ start 1))))) (define stream->list (lambda (str n) (if (<= n 0) '() (cons (stream-car str) (stream->list (stream-cdr str) (- n 1)))))) (define print-stream (lambda (str items) (if (<= items 0) (begin (display "...")(newline)) (begin (write (stream-car str)) (display ", ") (print-stream (stream-cdr str)(- items 1)))))) (define natzahlen (nat-stream 0)) (define fib_menge print-stream) ; angepasster Prozedurnamen (define generiere_fib_menge (lambda (f) (stream-map number->string (stream-map f natzahlen))))

ÜA: Geben Sie fur die Menge FIBS der Fibonacci-Zahlwörter eine Aufzählfunktion an und begründen Sie deren Berechenbarkeit. Weisen Sie nach, dass FIBS eine semi-entscheidbare Menge ist. Zeigen Sie, dass FIBS sogar entscheidbar ist.

Laut der Definition aus der Vorlesung Berechenbarkeitstheorie und Kreativität ist eine Menge aufzählbar, wenn es eine totale berechenbare Funktion f gibt, welche die Menge $\N$ auf eine Menge M abbildet.

In diesem Beispiel handelt es sich bei der Menge M um die Fibonacci-Zahlwörter. Die Aufzählprozedur f lautet wie folgt:

$$f(n) = \begin{cases} g(n), & \text{wenn } g(n) \in \text{ M};\\ 0, & sonst. \end{cases}$$

Damit die Funktion f eine surjektiv Abbildung der natürlichen Zahlen auf die Menge der Fibonacci-Zahlwörter und berechenbar ist, wird die Aufzählfunktion g benötigt.

$$g(n) = \begin{cases} 0, & \text{wenn } n=0;\\ 1, & \text{wenn } n=1;\\ (n-1) + (n-2), & sonst. \end{cases}$$

Scheme-Prozedur für die Aufzählfunktion g:

(define g (lambda (n) (cond ((= n 0) 0) ((= n 1) 1) (else (+ (g(- n 1)) (g(- n 2)))))))

(g 10)

ausführen

Erzeugen der Menge M an Fibonacci-Zahlwörter:

(define fibonacci_zahlen (generiere_fib_menge g))

(fib_menge fibonacci_zahlen 5)

ausführen

Um nachweisen zu können, dass die Funktion f semi-entscheidbar ist, muss es wie oben definiert folgende Funktion geben

$$\chi'_{M}(w) = \begin{cases} wahr, & \text{wenn } w \in \text{ M};\\ \bot, & sonst. \end{cases}$$

welche berechenbar ist. Mit Hilfe der Prozedur semi_chi_fib ist dies nachweisbar.

(define semi_chi_fib (lambda (m w) (letrec (( helfer ( lambda ( stm ) (if (string=? w (stream-car stm )) #t (helfer (stream-cdr stm )))))) (helfer m ))))

(semi_chi_fib fibonacci_zahlen "5")

ausführen

(semi_chi_fib fibonacci_zahlen "-1") ;user break

ausführen

ÜA: Übertragen Sie die vorhergehende Übungsaufgabe sinngemäß auf die Menge der Quadratzahlen $QZ = \{n^2 |n \in \N\}.$

Analog zur vorhergehenden Übungsaufgabe lässt sich folgende Aufzählprozedur f aufstellen:

$$f(n) = \begin{cases} g(n), & \text{wenn } g(n) \in \text{ M};\\ 1, & sonst. \end{cases}$$

Die Auzählfunktion g2, welche die Menge der quadtratischen Zahlen zurückgibt ist folgende:

(define g2 (lambda (n) (* n n)))

Erzeugen der Menge M an Quadratzahlen:

(define quad_menge print-stream) (define generiere_quad_menge (lambda (f) (stream-map f natzahlen)))

(define quad_zahlen (generiere_quad_menge g2))

(quad_menge quad_zahlen 9)

ausführen

Nachweis das die Funktion f semi-entscheidbar ist: Prozedur semi_chi_quad

(define generiere_quad_menge_wortmenge (lambda (f) (stream-map number->string (stream-map f natzahlen)))) (define quad_zahlen_2 (generiere_quad_menge_wortmenge g2))

(define semi_chi_quad (lambda (m w) (letrec (( helfer ( lambda ( stm ) (if (string=? w (stream-car stm )) #t (helfer (stream-cdr stm )))))) (helfer m ))))

(semi_chi_quad quad_zahlen_2 "9")

ausführen

(semi_chi_quad quad_zahlen_2 "3"); user break

ausführen

Nachweis das die Funktion ebenfalls entscheidbar ist:

(define f_help (lambda (n ls) (cond ((null? ls) #f) ((= n (car ls)) #t) (else (f_help n (cdr ls))))))

(define f (lambda (n) (if (f_help (g2 n) (stream->list quad_zahlen (+ n 1))) (g2 n) 1)))

(f 10)

ausführen

(f 10.1)

ausführen

Übung 4

Teilaufgabe 2 - Beweis Teil 2 (Tobias Salzmann, Ronald Krause)

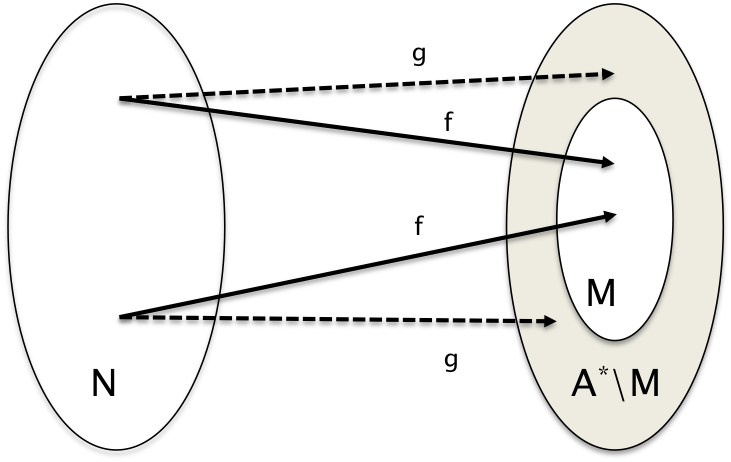
zu zeigen: Wenn M und $A^*$\M aufzählbare Mengen sind, dann ist M eine entscheidbare Menge.

Da M und $A^*$\M aufzählbare Mengen sind, gibt es total berechenbare surjektive Funktionen für diese.

Für M lautet die Auzählfunktion $f: \N \mapsto M$:

$$f(n) = \begin{cases} f(n), & \text{wenn } f(n) \in M;\\ a, & sonst \end{cases}$$

Hinweis: $a \in M$ .

Für $A^*$\M lautet die Auzählfunktion $g: \N \mapsto A^*$\M:

$$g(n) = \begin{cases} g(n), & \text{wenn } g(n) \in A^*\text{ \M};\\ b, & sonst \end{cases}$$

Hinweis: $b \in A^*$\M .

Beweis

Da zu zeigen ist, dass M entscheidbar sein soll, muss es eine total berechenbare Funktion $\chi_M$ geben.

$$\chi_M(w) = \begin{cases} wahr, & \text{wenn } w \in M;\\ falsch, & \text{wenn } w \in A^*\text{ \ M} \end{cases}$$

Es muss also eine Prozedur chi geben, welche für jedes Wort $w$ in endlicher Zeit für ein $i$ mit w = f(i) oder w = g(i) findet.

Da die Schnittmenge von M und $A^*$\M eine leere Menge ist, kann es kein w geben, welches in beiden Mengen vorkommt, sodass man genau sagen kann, ob w in der Menge M oder der Menge $A^*$\ M liegt.

$$M \cap (A^*\text{ \ M}) = \empty,\text{ gilt} f(i) = g(j) = w \text{ ausgeschlossen}$$

Da das Wort w aus der Wortmenge $A^*$ stammt und die Vereinigung der beiden Mengen die Wortmenge ist, muss das Wort in diesen beiden Mengen liegen. Um die Abzählbarkeit zu gewährleisten, wird abwechseln das $i$-te-Element aus $f$ und $g$ gesucht, sodass kein Wort vergessen wird.

$$\chi_M(w) = \begin{cases} wahr, & \text{wenn } f(i) = w;\\ falsch, & \text{wenn } g(i) = w \end{cases}$$

RAM-Programm: (Tobias Salzmann und Ronald Krause)

introot(a):= Module({x = a, y = 1}, WHILE( x > y) x = Quotient(x + y, 2); y = Quotient(a, x); return x; )

Befehlszähler	Befehl	Bemerkung
1	R0 = n	Berechnung Wurzel 25
2	R1 = RO	X
3	R2 = 1	Y
4	R20 = R1
5	R21 = R2
6	GOTO 36	Größer/KleinerVergleich
7	IFZERO R23 GOTO 9
8	STOP	Ergebnis x in R1
9	R3 = 0
10	R3 += R1	0 + x
11	R3 += R2	x + y
12	R4 = 2
13	R10 = 0	Wert zur Überprüfen des Rücksprunges
14	GOTO 22	Division
15	R1 = R5	neues x in R1
16	R3 = R0	n in R3
17	R4 = R1	x in R4
18	R10 = 1	Wert zur Überprüfung des Rücksprunges
19	GOTO 22	Division
20	R2 = R5	neues y in R2
21	GOTO 36	Größer/Kleinervergleich

Ganzzahlige Division

q = 0; r = a; while (r>=b) { q = q+1; //Ganzzahliger Wert r = r-b; //Ganzzahliger Rest }

Befehlszähler	Befehl	Bemerkung
22	R9 = 1
23	R5 = 0
24	R6 = R3	Zähler für 1.Zahl
25	R7 = R4	Zähler für 2.Zahl
26	IFZERO R7 GOTO 31	Größer/Kleinervergleich
27	R7 -= R9	1 mal subtrahieren
28	IFZERO R6 GOTO 34
29	R6 -= R9	1 mal subtrahieren
30	GOTO 26
31	R5 += R9	1 mal addieren
32	R6 -= R7
33	GOTO 24

Größer/Kleinervergleich

Befehlszähler	Befehl	Bemerkung
34	IFZERO R10 GOTO 15
35	GOTO 20

Befehlszähler	Befehl	Bemerkung
36	IFZERO R20 GOTO 41	x
37	R20 -= R9
38	IFZERO R21 GOTO 42	y
39	R21 -= R9
40	GOTO 36
41	R23 = 1
42	GOTO 7	Wenn R23 = 1; dann ist x <= y und wenn R23 = 0, dann x > y