siinkoer
Aus ProgrammingWiki
Aufgabe 3 (Ingo Körner, Christof Ochmann)
Zeigen Sie, dass die folgenden Mengen abzählbar unendlich sind: $\Z, \Q$, die Menge der Primzahlen, die geraden Zahlen.
Für $\Z$:
| 0 | 1 | 2 | 3 | 4 | 5 | ... |
| 0 | 1 | -1 | 2 | -2 | 3 | ... |
$$f(n) = \begin{cases}
-\frac{n}{2}, & \text{wenn n gerade};\\
\lceil \frac{n}{2} \rceil, & \text{sonst }.\\
\end{cases}$$
Für $\Q$:
| $\Z$\$\N$ | $1$ | $2$ | $3$ | $4$ | $5$ | ... |
|---|---|---|---|---|---|---|
| 1 | 1/1 | 1/2 | 1/3 | 1/4 | 1/5 | ... |
| 2 | 2/1 | 2/2 | 2/3 | 2/4 | 2/5 | ... |
| 3 | 3/1 | 3/2 | 3/3 | 3/4 | 3/5 | ... |
| 4 | 4/1 | 4/2 | 4/3 | 4/4 | 4/5 | ... |
| 5 | 5/1 | 5/2 | 5/3 | 5/4 | 5/5 | ... |
| ... | ... | ... | ... | ... | ... | ... |
Es werden mit Hilfe des ersten Cantorschen Diagonalisierungsverfahren alle Zahlen erreicht.
Für die Menge der Primzahlen:
1. Die Menge der Primzahlen P ist unendlich (nach Satz von Euklid).
2. Die Menge der Primzahlen P ist abzählbar unendlich, da gilt: P $\subset \N$.
Für die Menge der geraden Zahlen:
1. Die geraden Zahlen G sind unendlich (per Definition) und abzählbar unendlich, da gilt: G $\subset \Z$.
Aufgabe 4 (Ingo Körner, Christof Ochmann)
ÜA: Zeigen Sie, dass jede endliche Menge M aufzählbar ist.
aufzählbar = abzählbar + berechenbar
1) Jede endliche Menge ist aufzählbar (per Definition).
2) Jede endliche Menge ist berechenbar.
Es gibt eine Funktion f, die als Eingabe die natürlichen Zahlen N nimmt und auf jedes Element der endlichen Menge M abbildet. f ist berechenbar, da es eine total berechenbare surjektive Funktion f : N -> M gibt. Es wird der Reihe nach jedes Element aus N einem Element aus M zugeordnet. Ist f sujektiv, können die restlichen Elemente aus N auf ein beliebiges Element von M abgebildet werden. Somit ist f surjektiv, total und berechenbar.
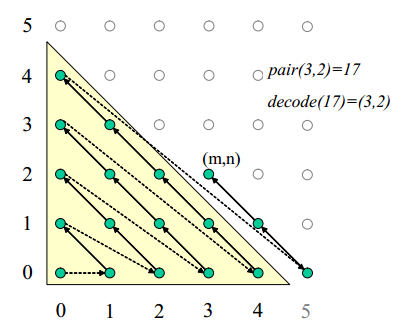
ÜA: Die Menge G der Gitterpunkte (0, 0),(0, 1), ... einer x-y-Ebene ist aufzählbar.
1 Geben Sie eine Funktion f an, die $\N_0$ bijektiv auf G abbildet.
2 Definieren Sie eine Ordnungsrelation $p_<$ in G.
$(G, p_<)$ = {(0,0) < (0,1) < (1,0) < (2,0) < (1,1) < (0,2) < (0,3) < (1,2) < (2,1) < ...}
3 Geben Sie eine Funktion k zur Berechnung der Platznummer k(x, y) des betrachteten Gitterpunktes (x, y) an.
4 Geben Sie eine Aufzählprozedur für G an und begründen Sie deren Berechenbarkeit.
Teilaufgabe 1 - Beweis Teil 1 (Ingo Körner, Christof Ochmann)
Hinrichtung des Satzes: Wenn M eine entscheidbare Menge ist, dann sind M und $A^*$\M aufzählbare Mengen.
Beweis: Aus der Entscheidbarkeit von M folg semi-Entscheidbarkeit von M und \M. Jede semi-entscheidbare Menge M ist aufzählbar. Es gibt eine Aufzählfunktion f für M. Sie wird auch Contorsche Paarungsfunktion genannt.
$$f(z) = \begin{cases} g(x), & \text{wenn $\chi'_M$(g(x)) = wahr innerhalb von Zeit y};\\ a, & \text{wenn Proz. für $\chi'_M$(g(x)) innerhalb y ohne Ergebnis}.\\ \end{cases}$$ wobei a $\in$ M, wenn $M \neq \emptyset$
$$g(x) = \begin{cases} w, & \text{w $\in$ M};\\ \perp, & \text{sonst}.\\ \end{cases}$$
Turing-Aufzählbarkeit, Turing-Entscheidbarkeit (Max Wielsch, Raik Bieniek, Ingo Körner, Christof Ochmann)
Definieren Sie die Begriffe Turing-aufzählbar und Turing-entscheidbar analog zur Turing-Berechenbarkeit.
Sei A ein Alphabet, $M \subseteq A^*$. M heißt Turing-entscheidbar, falls die charakteristische Funktion $\chi_M$ Turing-berechenbar ist.
M heißt Turing-aufzählbar, wenn es eine Funktion $f: N \rightarrow M$ gibt, die surjektiv und Turing-berechenbar ist.
Aufgabe 1 (Ingo Körner, Christoph Ochmann)
(Aufgabe siehe: VL Slide 13)
Zeigen Sie die Unentscheidbarkeit (Semi-Entscheidbarkeit) von $L_{\Sigma^{*}}:=\{\left\langle M \right\rangle | L(M) = \Sigma^{*} \}$ durch Reduktion der Sprache $L_{\Sigma^{*}}$ auf das Halteproblem.
Schreibe für alle Eingabewörter aus $\Sigma^{*}$ die Kodierung der Maschine M, d.h. <M>, sowie w $\in$ $\Sigma^{*}$ auf das Band einer Maschine $M_2$. Die Maschine $M_2$ ist so konstruiert, dass sie aus ihrer Eingabe <M> und w die Kodierung einer Maschine M', d.h. <M'>, zusammen mit einem Eingabewort y auf ihr Band als Ausgabe schreibt. Die Besonderheit von M' ist, dass diese Maschine mit dem Eingabewort y stoppt, wenn M(w) stoppen würde. Dabei ist y nur ein Platzhalter, denn y hat auf die Terminierung von M' keinen Einfluss. Als nächstes wird <M'> und y auf das Band einer UTM $M_1$ geschrieben. $M_1$ führt die Kodierung der Maschine M' mit dem Wort y aus. Dabei verwirft die Maschine M' als erstes ihr Eingabewort y, so dass ihr Band leer ist. Wenn die durch $M_1$ ausgeführte Maschine M' mit ihrem leeren Band hält, so heißt das, dass auch die Maschine M mit dem Wort w akzeptieren würde. Wenn die durch die Maschine $M_1$ ausgeführte Maschine M' auf dem anfangs leeren Band nicht in einem Endzustand hält, dann stoppt auch die Maschine M mit dem Wort w nicht in einem Endzustand. <M> ist $\in$ $L_{\Sigma^{*}}$ genau dann, wenn M' termiert.
Reduktionsreihenfolge (Ingo Körner, Christof Ochmann)
- Zeigen Sie dass es von der Reduktionsreihenfolge abhängen kann, ob die für (($\lambda$ y. z)(($\lambda$ x. (x x))($\lambda$ x. (x x)))) existierende Normalform z gefunden wird oder nicht.
Linksaußen-Reduktion $\beta_0$: $((\lambda y.z)((\lambda x.(x \text{ } x))(\lambda x.(x \text{ } x)))) \xrightarrow{\beta_0} z$
Linksinnen-Reduktion $\beta_i$: $((\lambda y.z)((\lambda x.(x \text{ } x))(\lambda x.(x \text{ } x)))) \xrightarrow{\beta_i} ((\lambda y.z)((((\lambda x.(x \text{ } x))(\lambda x.(x \text{ } x))))))$
Da sich durch die Linksinnen-Reduktion an der Formel nichts verändert hat, ist sie endlos reduzierbar.
- Verwenden Sie zur Berechnung von (($\lambda$x. ((x d)(($\lambda$ y. (x y)) a))) b) unterschiedliche Reduktionsreihenfolgen.
Linksaußen-Reduktion $\beta_0$: $((\lambda x.((x \text{ } d)((\lambda y.(x \text{ } y))a)))b) \xrightarrow{\beta_0} ((b \text{ } d)((\lambda y.(b \text{ } y))a)) \xrightarrow{\beta_0} ((b \text{ } d)(((b \text{ } a))))$
Linksinnen-Reduktion $\beta_i$: $((\lambda x.((x \text{ } d)((\lambda y.(x \text{ } y))a)))b) \xrightarrow{\beta_i} ((\lambda x.((x \text{ } d)(((x \text{ } a))))) b) \xrightarrow{\beta_i} ((b \text{ } d)(((b \text{ } a))))$