sifenits
Aus ProgrammingWiki
- präfix: BuK/IIm11/Studenten/sifenits
Prinzip der Gödelisierung (Daniel Tasche, Jens Heider, Felix Nitsche, Stefan Lüttke)
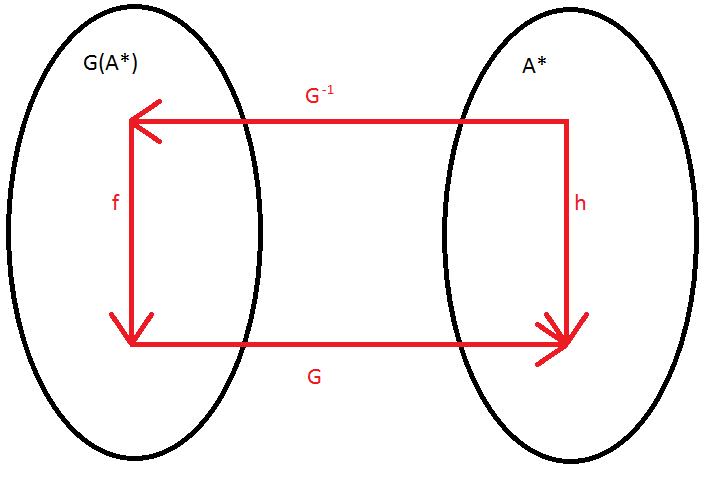
$f : G(A^*) \rightarrow G(A^*) und h : A^* \rightarrow A^*$ sind Funktionen. $f$ ist eine berechenbare Funktion genau dann, wenn $h$ eine berechenbare Funktion ist.
Beweis als Übungsaufgabe: argumentativ für $h = G^{-1} \circ f \circ G$ und $f = G \circ h \circ G^{-1}$ unter Bezugnahme auf das Prinzip der Gödelisierung.
Da G und G^{-1} berechenbar sind, lassen sich $f(x)$ oder $h(x)$ mit den jeweils verbleibenden Funktionen ausdrücken.
- wenn $f$ berechenbar ist:
$h(x) = G(f(G^{-1}(x)))$
- wenn $h$ berechenbar ist:
$f(x) = G^{-1}(h(G(x)))$