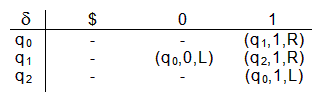BuK-KA-UTM
Aus ProgrammingWiki

Inhaltsverzeichnis |
Deutschmann, Horbach
Aufgabenstellung
Mithilfe von kfg Edit aus ATOCC soll zuerst die Sprache der TM-Codierungen durch die Grammatik $G$ definiert werden.
Anschließend soll eine Turingmaschine $M$ in Autoedit beschrieben und die Anwendung von $M$ auf verschiedene Eingabewörter simuliert werden.
Die TM $M$ soll danach mit $G$ kodiert werden.
Aufbauend auf $G$ soll nun ein Compiler erstellt werden, der die Codierung von $M$ in eine von ATOCC lesbare Form (XML Dokument) kompiliert.
Die Aufgabenstellung dieser Kreativaufgabe ist hier zu finden. Nach Fertigstellung der Aufgabe soll der fertige Compiler im Compilerwiki hochgeladen und verlinkt sein.
Nach Hochladen des Compilers trat jedoch ein Fehler auf:
Parse error at line 1, column 2 : Error or number too big for integer type: 101101101101101101010101011011011101101101110110101101001011
Bei normaler Ausführung des Compilers, wird jedoch das XML-Dokument für Autoedit wie gewünscht erzeugt.
Grammatik der TM-Codierungen
G = (N, T, P, s)
N = {TMcodierung, Trenner, Endzustaende, Delta, Uebergang, Kopfbewegung, L, R, N, Zeichen, Null, Eins, B, Zustand, Einsenfolge}
T = {0, 1}
P = {
TMcodierung -> Delta Trenner Endzustaende
Trenner -> 0 0
Endzustaende -> Zustand 0 Endzustaende
| Zustand
Delta -> Uebergang 0 Delta | Uebergang
Uebergang -> Zustand 0 Zeichen 0 Zustand 0 Zeichen 0 Kopfbewegung
Kopfbewegung -> L | R | N
L -> 1
R -> 1 1
N -> 1 1 1
Zeichen -> Null | Eins | B
Null -> 1
Eins -> 1 1
B -> 1 1 1
Zustand -> Einsenfolge
Einsenfolge -> 1 | 1 Einsenfolge
}
s = TMcodierung
Die Turingmaschine M
Als Beispiel soll die Turingmaschine M mit folgender Definition dienen:
$M = (\{q_0, q_1, q_2\}, \{0, 1\}, \{\$, 0, 1\}, \delta, q_0, \$, \{q_0, q_1\})$
Simulation der TM
Die Turingmaschine stoppt für folgende Wörter:
- $\epsilon$
- 0
- 1
- 0101010110
Die Turingmaschine stoppt in einem Nicht-Endzustand für die Wörter:
- 11
- 111
- 1111
Die Turingmaschine stoppt nicht für:
- 10
Kodierung der TM
Die Turingmaschine soll nun unter Verwendung der folgenden Kodierungsregeln per Hand kodiert werden:
| Symbol | Kodierung |
| 0 | 1 |
| 1 | 11 |
| B | 111 |
| $q_0$ | 1 |
| $q_1$ | 11 |
| $\vdots$ | $\vdots$ |
| $q_n$ | $1^{n+1}$ |
| L | 1 |
| R | 11 |
| N | 111 |
(q0,1) = (q1,1,R) 1 0 11 0 11 0 11 0 11
(q1,0) = (q0,0,L) 11 0 1 0 1 0 1 0 1
(q1,1) = (q2,1,R) 11 0 11 0 111 0 11 0 11
(q2,1) = (q0,1,L) 111 0 11 0 1 0 11 0 1
Fasst man nun die einzelnen Kodierungen zusammen ergibt das die folgenden Teilkodierung:
1011011011011 0 1101010101 0 110110111011011 0 1110110101101
Für eine vollständige Kodierung fehlen noch die Endzustände, welche durch den Trenner (00) abgetrennt werden:
Endzustände: 1 0 11 Turingmaschine (gesamt): 1011011011011 0 1101010101 0 110110111011011 0 1110110101101 00 1011
Die Compiler-Zielsprache
Die Zielsprache des Compilers ist die AtoCC-Repräsentation einer Turingmaschine (d.h. ein XML-Dokument für Autoedit). Der Hinweis im Aufgabenblatt ist sehr wichtig. Demnach muss man die Regel $\text{Trenner}$ $\to$ $0$ $0$ streichen und dafür später im Scanner ein Token definieren.
Die reduzierte Grammatik ist dann wie folgt:
G = (N, T, P, s)
N = {TMcodierung, Trenner, Endzustaende, Delta, Uebergang, Kopfbewegung, L, R, N, Zeichen, Null, Eins, B, Zustand, Einsenfolge}
T = {0, 1}
P = {
TMcodierung -> Delta Trenner Endzustaende
Endzustaende -> Zustand 0 Endzustaende
| Zustand
Delta -> Uebergang 0 Delta | Uebergang
Uebergang -> Zustand 0 Zeichen 0 Zustand 0 Zeichen 0 Kopfbewegung
Kopfbewegung -> L | R | N
L -> 1
R -> 1 1
N -> 1 1 1
Zeichen -> Null | Eins | B
Null -> 1
Eins -> 1 1
B -> 1 1 1
Zustand -> Einsenfolge
Einsenfolge -> 1 | 1 Einsenfolge
}
s = TMcodierung
Nachdem aus dieser Grammatik ein Compiler exportiert wurde, kann man nun im VCC ein Token für $0$ $0$ definieren. Das behebt das Shift-Reduce Problem.
Die XML-Struktur des Zieldokumentes entspricht nach Weglassen von Zusatzinformationen dem folgenden Aufbau:
Die entfernten Elemente befinden sich im LAYOUT-Block. Innerhalb dieses Blockes stehen Angaben zum Simulationsinput, zur Darstellung des Übergangsgraphen und zur verwendeten Schriftart. Diese Angaben sind nicht Bestandteil der durch $G$ definierten Sprache und somit werden sie nicht benötigt. AtoCC kann mit dem Fehlen der Angaben umgehen, da es Vorgabewerte verwendet.
Der Compiler
Der Compiler wurde mithilfe von kfg Edit nach VCC exportiert. In VCC folgten die Einstellungen für einen Java-Compiler und LALR(1) für den Parsertyp. Anschließend wurde das Token für die entfernte Trenner-Regel angelegt.
Als Parserdefinition wurde der folgende Code verwendet:
Nach der Angabe des globalen Java Codes wurden die Verarbeitungsschritte für die einzelnen Token festgelegt. Diese können in der VCC-Darstellung eingesehen werden.
Die durch den Compiler erzeugte XML-Datei kann in AutoEdit geladen werden. Eine Übereinstimmung mit der ursprünglichen Turingmaschine $M$ lässt sich sehr einfach in der Darstellung der Übergangstabelle feststellen.
Link zum fertigen TM-Compiler
TODO