BuK-Übung07
Aus ProgrammingWiki

Eigenschaften der Gödelisierung (Stefan Scheumann, Ronald Krause, Tobias Salzmann, Robert Rosenberger)
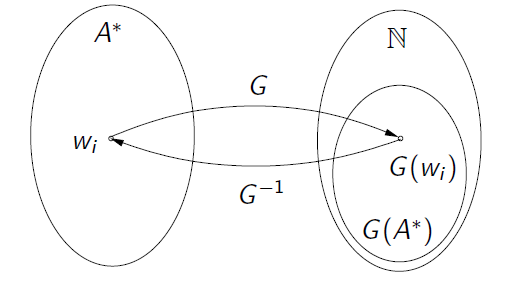
Eine Abbildung $G : A^* \rightarrow \N$ heißt Gödelisierung von $A^*$, wenn die folgenden Bedingungen erfüllt sind:
(1) $G$ ist injektiv, d.h. für alle $w, w'\in A^*$ gilt: Wenn $w \neq w'$, dann $G(w) \neq G(w^')$
(2) $G$ ist berechenbar, d.h. zu jedem Wort $w \in A^*$ lässt sich $G(w)$ in endlich vielen Schritten berechnen.
(3) $G(A^*)$ ist entscheidbar, d.h. für jedes $n \in \N$ lässt sich in endlich vielen Schritten feststellen, ob $n \in G(A^*)$ gilt oder nicht.
(4) Die Umkehrfunktion $G^{-1} : G(A^*) \rightarrow A^*$ ist berechenbar, d.h. zu jedem $n \in G(A^*)$ lässt sich das Wort $w$ mit $G(w) = n$ in endlich vielen Schritten auffinden. (Übungsaufgabe: (4) folgt aus (1)-(3).)
z.z. ist, dass Bedingung 4 aus den ersten drei Eigenschaften folgt.
$G$ ist die Funktion für $A^* \rightarrow \N$.
$G(A^*)$ ist die Menge von Gödelnummern.
(1) Jedes Wort aus der Definitionsmenge $A^*$ hat einen Funktionswert $G(w)$.
(2) Es gibt eine Prozedur, welche zu jedem Wort aus $A^*$ (genau eine) Gödelnummer zurückgibt.
(3) Es gibt eine Prozedur, welche entscheidet, ob eine natürliche Zahl eine Gödelnummer ist oder nicht.
Laut Bedingung 4 gibt es eine Umkehrfunktion, welche ein Wort aus $A^*$ für eine Gödelnummer zurückgibt. Das heißt, dass zu jeder natürlichen Zahl, welche zur Menge $G(A^*)$ gehört, sich das Wort $w$ mit $G(w)=n$ in endlich vielen Schritten zurückgibt.
Aus Bedingung (3) ergibt sich, dass für jede natürliche Zahl entschieden werden kann, ob es eine Gödelnummer ist oder nicht.
Aus Bedingung (2) kann zu jeden Wort $w$ aus $A^*$ eine Gödelnummer bestimmt werden.
Aus (3) und (2) folgt, dass beide Gödelnummern miteinander verglichen werden können, wodurch bei einer Gleichheit der Gödelnummern, dass Wort $w$ aus $A^*$ zurückgegeben werden kann.
Aus der Injektivität lt. (1) ergibt sich, dass es für ein Wort $w$ aus $A^*$ eine Gödelnummer gibt, sodass das Wort nach einer Übereinstimmung der Gödelnummern eindeutig ist.
Durch die Aufzählfunktion für $A^*$ werden alle möglichen Wörter aus der Wortmenge betrachtet.
Primzahlverschlüsselung (Ingo Körner, Christof Ochmann, Raik Bieniek, Max Wielsch)
Schreiben Sie Prozeduren für G (Primzahlverschlüsselung) und $G^{−1}$:$G(A^∗)→A^∗$. Erzeugen Sie auch den Stream für $A^∗$ bei gegebenem Alphabet A unter Verwendung der Primzahlverschlüsselung als Gödelisierung. Dokumentieren Sie die Verwendung der Prozeduren im ProgrammingWiki.
Die Gödelisierung bezeichnet das Verfahren, ein Wort aus einer Wortmenge ($A^*$) auf die Menge der Zahlen abzubilden. Dadurch sind Probleme der "Wort-Welt", also Probleme, die mit Programmiersprachen beschrieben werden können, ebenso in der Zahlenwelt (Mathematik) darstellbar und lösbar (sofern sie ebenso durch ein Programm lösbar sind).
Hilfsprozeduren
Stream-Prozeduren
Prozeduren für Wortmengen-Stream
Prozeduren für Primzahlenverschlüsselung
Hauptprozedur
Die Hauptprozedur für die Gödel-Funktion ist nun mit den Hilfsfunktionen realisiert.
Umkehrung der Gödelisierung
Für die "Ent-Gödelisierung" muss nun aus einer Gödelnummer ein Wort aus der Wortmenge (Das Urbild der Abbildung) erzeugt werden, das mit der Gödel-Funktion benutzt wieder genau dieselbe Gödelnummer ergibt.
Hilfsprozeduren
Hauptprozedur
Prinzip der Gödelisierung (Daniel Tasche, Jens Heider, Felix Nitsche, Stefan Lüttke)
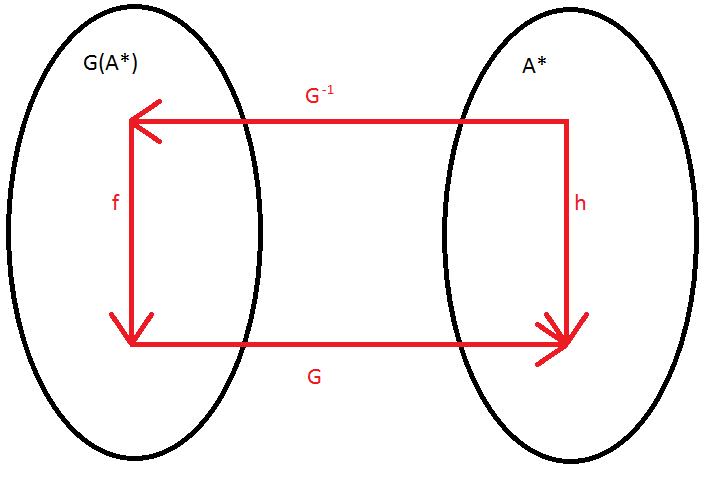
$f : G(A^*) \rightarrow G(A^*) und h : A^* \rightarrow A^*$ sind Funktionen. $f$ ist eine berechenbare Funktion genau dann, wenn $h$ eine berechenbare Funktion ist.
Beweis als Übungsaufgabe: argumentativ für $h = G^{-1} \circ f \circ G$ und $f = G \circ h \circ G^{-1}$ unter Bezugnahme auf das Prinzip der Gödelisierung.
Da G und G^{-1} berechenbar sind, lassen sich $f(x)$ oder $h(x)$ mit den jeweils verbleibenden Funktionen ausdrücken.
- wenn $f$ berechenbar ist:
$h(x) = G(f(G^{-1}(x)))$
- wenn $h$ berechenbar ist:
$f(x) = G^{-1}(h(G(x)))$