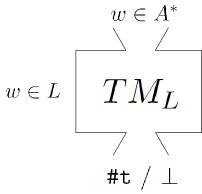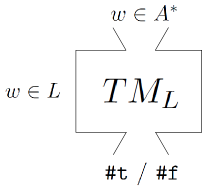BuK-Übung05
Aus ProgrammingWiki

Inhaltsverzeichnis |
Mathematik vs. Informatik
Aufgabe 1 (Stefan Scheumann, Robert Rosenberger, Tobias Salzmann, Ronald Krause)
Defnieren Sie je eine totale Funktion für den Vorgänger und die Halbierung einer natürlichen Zahl. Defnieren Sie außerdem eine Funktion mit $ D_f = \N \setminus \{1234, 7266281\} $.
Lösung:
Funktionsdefinition Vorgänger (total) : $ f(n) = n - 1$
Funktionsdefinition Vorgänger (partiell) : $$ f(n) = \begin{cases} n - 1 ; & \text{für } n \in \N \setminus \{1234, 7266281\};\\ \bot; & sonst \end{cases} $$
Funktionsdefinition Halbiering (total) : $ f(n) = n / 2$
Funktionsdefinition Vorgänger (partiell) : $$ f(n) = \begin{cases} n / 2 ; & \text{für } n \in \N \setminus \{1234, 7266281\};\\ \bot; & sonst \end{cases} $$
Aufgabe 2 (Manuel Mauky)
Im Buch wird die Aussage getroffen, dass genau wie beim Halteproblem auch das Äquivalenzproblem für berechenbare Funktionen nicht allgemein entscheidbar ist. (siehe Kapitel 5.3, Seite 63). Diese Aussage gilt es zu begründen und praktische Konsequenzen für die Softwareverifikation abzuleiten. (Aufgabe 5.2 im Buch).
In diesem Konzext versteht man unter dem Äquivalenzproblem zu entscheiden, ob zwei beliebige Prozeduren die gleiche Funktion berechnen. Gibt es also eine Prozedur, die dies für zwei beliebige Prozeduren feststellt.
Äquivalent sind zwei Prozeduren also dann, wenn sie für sämtliche Eingabewerte $n$ das gleiche Resultat liefern. Das heißt insbesondere, dass beide Prozeduren nicht stoppen für Werte von $n$, für die $f(n)$ nicht definiert ist.
Ähnlich wie bei der Prozedur totalmacher könnte man sich hier eine Hilfsprozedur aequivalent_fuer_n? vorstellen, die zwei Prozeduren und ein Argument n entgegen nimmt und mit #t oder #f antwortet, je nach dem ob beide Prozeduren für dieses n äquivalent sind.
Beispiele:
Für totale Funktionen wie im Beispiel ist die Prozedur aequivalent_fuer_n leicht implementierbar. Man ruft nacheinander beide Prozeduren mit n als Argument auf und vergleich anschließend die zurückgegebenen Ergebnisse. Problematisch wird es jedoch, wenn $f(n)$ für ein gegebenen $n$ nicht definiert ist. Da keine Prozedur haelt_fuer_n? existiert, können wir beim ausführen der übergebenen Prozeduren nicht feststellen, ob diese jemals stoppen werden.
Was sind praktische Konsequenzen aus diesem Sachverhalt?
In der Softwareentwicklung kommt es vor, dass ältere Software-Komponenten zwar ihre fachlichen Aufgaben spezifikationsgemäß erfüllen, jedoch bestimmte nicht-funktionale Anforderungen nicht (mehr) erfüllen können. Soll eine solche Komponente durch eine neue Komponente ersetzt werden, muss überprüft werden, dass die fachliche Spezifikation nach wie vor erfüllt bleibt, es also keine ungewollten Nebeneffekte gibt.
Wäre das Äquivalenzproblem allgemein entscheidbar, könnte man ein Programm entwickeln, welches die fachliche Gleichheit und damit Austauschbarkeit sicherstellt. In der Praxis muss man jedoch nach wie vor auf unvollständige Hilfsmittel wie Unit-Tests ausweichen.
Ein konkretes Beispiel wäre ein Data-Access-Object für eine ältere Datenbank, welches durch eine Neu-Implementierung für eine andere Datenbank ersetzt werden soll. Dem Softwareentwickler bleibt nichts anderes übrig als sämtliche Funktionalität des DAOs in Unit-Tests zu prüfen. Tauscht er die Implementierung aus müssen alle Tests nach wie vor erfolgreich durchlaufen. Damit kann jedoch trotzdem nicht ausgeschlossen werden, dass für bestimmte Fälle das Verhalten unterschiedlich ist, weil z.B. gerade diese Fälle bei den Unit-Tests vergessen wurden.
Postsches Korrrespondenzprobelm PCP (Jens Heider, Daniel Tasche)
Aufgabe 1
Für K = ((001; 0)(01; 011); (01; 101); (10; 001)) gibt es eine Lösung. Die gesuchte Indexfolge heißt
(2 4 3 4 4 2 1 2 4 3 4 3 4 4 3 4 4 2 1 4 4 2 1 3 4 1 1 3 4 4 4 2 1 2 1 1 1 3 4 3 4 1 2 1 4 4 2 1 4 1 1 3 4 1 1 3 1 1 3 1 2 1 4 1 1 3)
Uberprüfen Sie die angegebene Lösung per Hand.
Lösung siehe Bild...
Aufgabe 2
Entwickeln Sie eine Scheme-Prozedur (ProgrammingWiki), die bei Aufruf für eine gegebene Instanz eine Lösung des PCP findet, falls eine solche existiert und der Rechenaufwand im Rahmen bleibt.
Turing-Maschine und Churchsche These
Turing-Maschine als Akzeptator (Stefan Lüttke, Felix Nitsche)
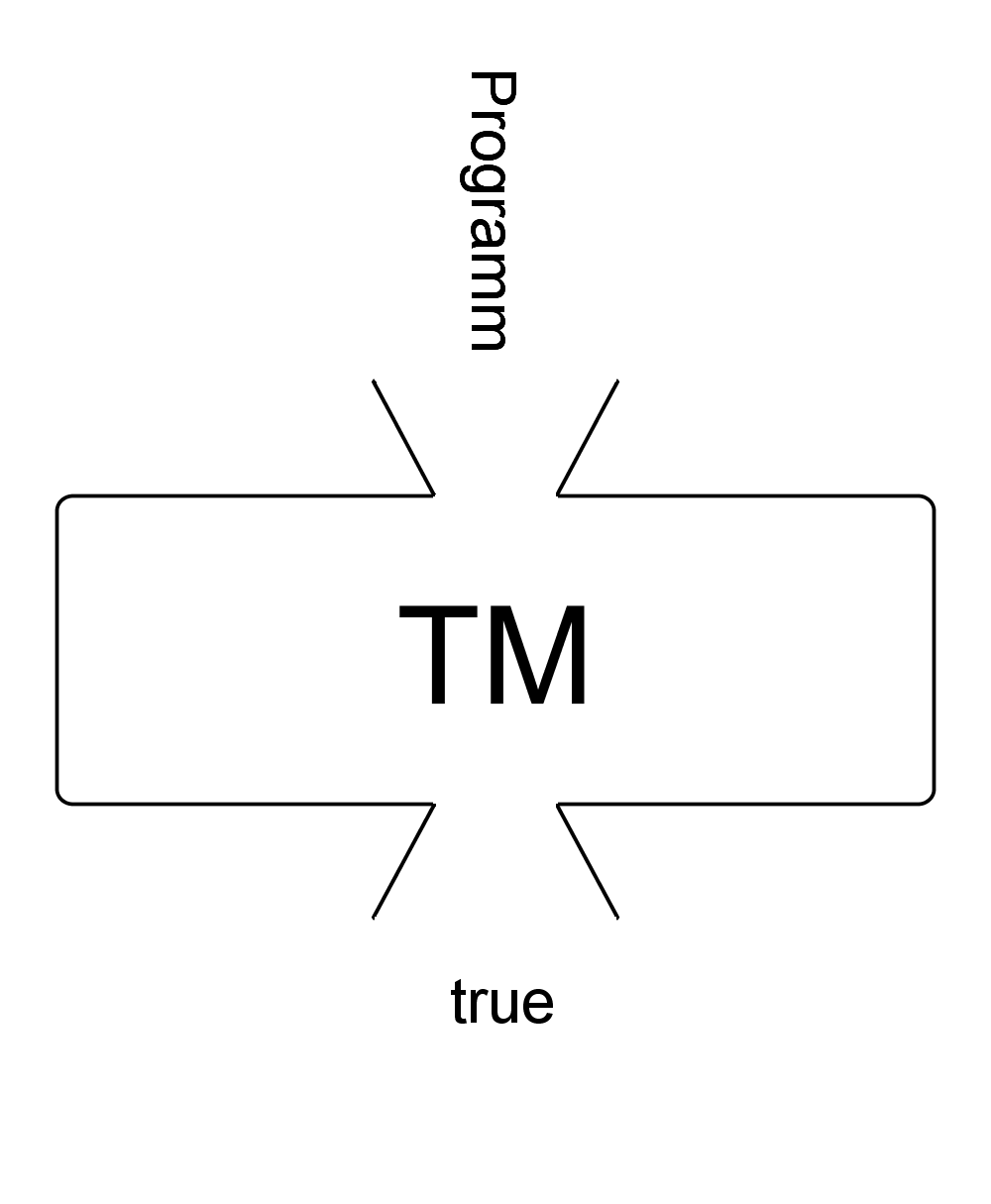
Geben Sie Trichterbilder für den Einsatz einer TM als Akzeptator an:
- für semi-entscheidbare Sprachen
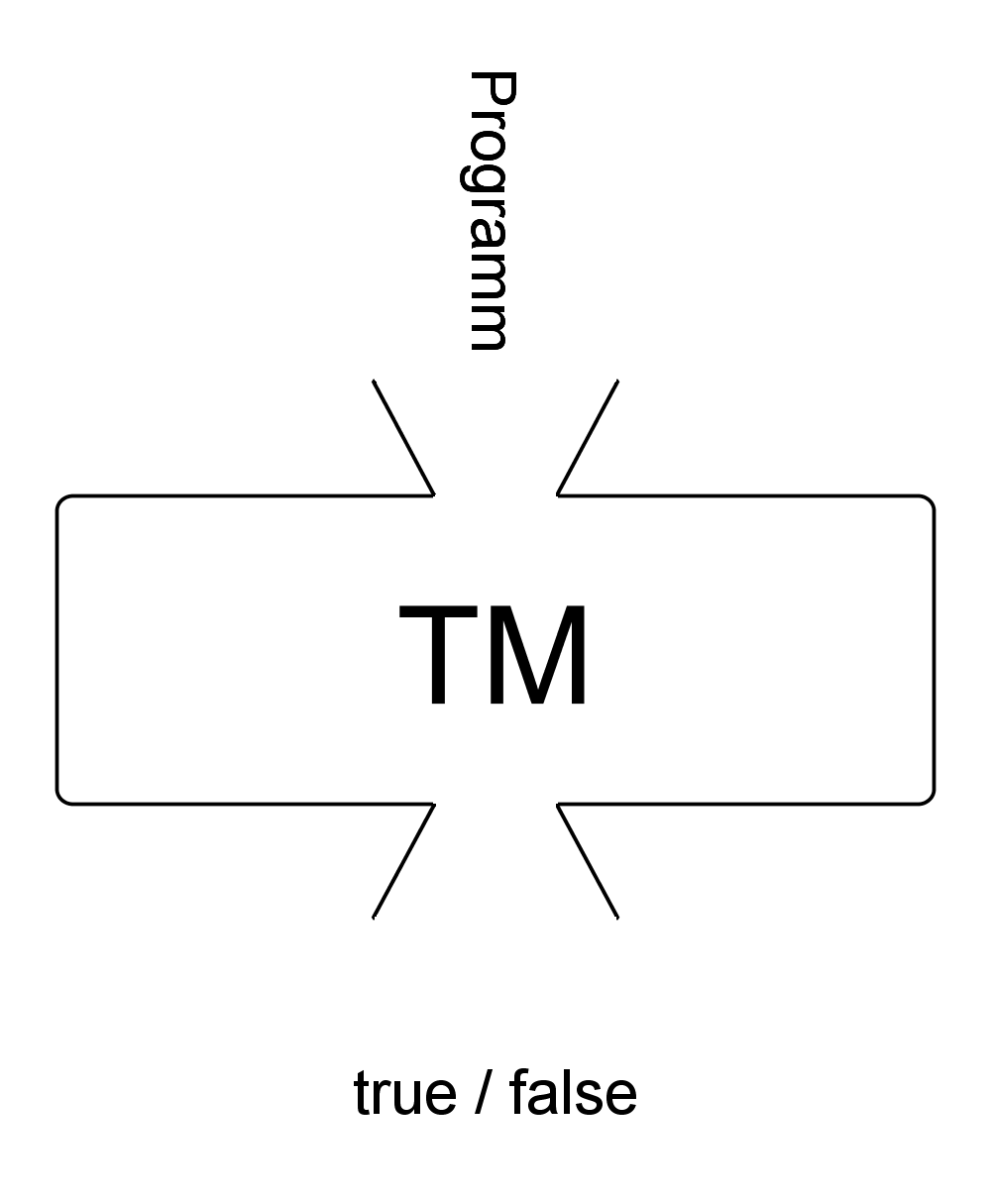
- für entscheidbare Sprachen
Turing-Aufzählbarkeit, Turing-Entscheidbarkeit (Max Wielsch, Raik Bieniek, Ingo Körner, Christof Ochmann)
Definieren Sie die Begriffe Turing-aufzählbar und Turing-entscheidbar analog zur Turing-Berechenbarkeit.
Sei A ein Alphabet, $M \subseteq A^*$. M heißt Turing-entscheidbar, falls die charakteristische Funktion $\chi_M$ Turing-berechenbar ist.
M heißt Turing-aufzählbar, wenn es eine Funktion $f: \N \rightarrow M$ gibt, die surjektiv und Turing-berechenbar ist.