BuK-Übung04
Aus ProgrammingWiki
Inhaltsverzeichnis |
Aufgabe 1
Satz 1: Eine Menge M ist genau dann aufzählbar, wenn sie semi-entscheidbar ist.
Teilaufgabe 1 (Jens Heider, Daniel Tasche, Felix Nitsche, Stefan Lüttke)
zu zeigen: Wenn $M$ aufzählbar, dann $M$ semi-entscheidbar.
Gegeben ist eine aufzählbare Menge. Daraus folgt, dass es eine Aufzählprozedur $f$ für $M$ gibt, welche die natürlichen Zahlen auf die Elemente von $M$ abbildet. $f : \N \mapsto M $
zu zeigen: $M$ ist semi-entscheidbar
Wenn $M$ semi-entscheidbar ist, dann gibt es eine Prozedur $\chi'_M$, die für ein Wort aus der Menge $M$ über dem Alphabet $A^*$ wahr zurückgibt, wenn das Wort in der Menge enthalten ist und ansonsten ewig weiter läuft. $\chi'_M(w) : A^* \mapsto \{\text{wahr}\}$
$$ \chi'_M(w) = \begin{cases} wahr; & \text{wenn } w \in M;\\ \bot; & sonst \end{cases} $$
Durch Verwendung der Prozedur $f$ kann entschieden werden, ob ein gegebenes Element in der Menge $M$ enthalten ist. Dabei wird $f$ für jedes $i$; mit $i \in \N$ aufgerufen, $f(0)$, $f(1)$, $f(2)$, ... Ergibt $f(i)$ das Wort, dann gibt $\chi'_M$ wahr zurück, ansonsten läuft die Prozedur ewig weiter.
$$ \chi'_M(w) = \begin{cases} wahr; & \text{wenn } f(i) = w; i \in \N;\\ \bot; & sonst \end{cases} $$
Teilaufgabe 2 (Tobias Salzmann, Ronald Krause, Robert Rosenberger, Stefan Scheumann)
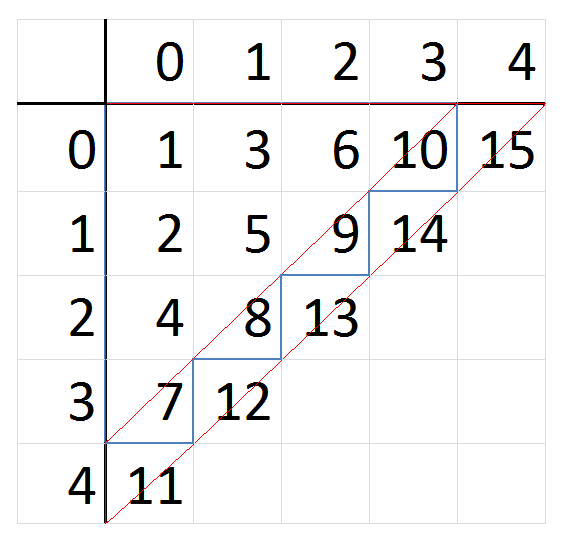
ÜA: Vervollständigen Sie die Herleitung der Funktionen für x und y aus $z = π(x, y)$ und geben Sie als Beispiel die Ermittlung von x und y aus $z = π(1, 3) = 13$ an.
Herleitung der Funktionen für $x$ und $y$ aus $z = (x; y)$
$z =\frac{(x+y)(x+y+1)}{2} +y = t + y;$
$w = x + y;$
$x,y,z \in \N, w,t \in \R_{0}^{+}$
$t = z - y = \frac{w(w+1)}{2} = \frac{w^{2}+w}{2} $
Die Lösung von $w^{2} + w + 2t = 0$
$w_{1,2}=-\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2-q}$
$w_{1,2}=-\frac{1}{2} \pm \sqrt{\left(\frac{1}{2}\right)^2+2t}$
$w_{1,2}=-\frac{1}{2} \pm \sqrt{\frac{1}{4}+\frac{8t}{4}}$
$w_{1,2}=-\frac{1}{2} \pm \sqrt{\frac{1+8t}{4}}$
$w_{1,2}=-\frac{1}{2} \pm \frac{\sqrt{1+8t}}{2}$
für positives $w$ ist $w_1 = \frac{\sqrt{8t+1}-1}{2}$
Außerdem gilt:
$t \leq z $, weil $z=t+y$
$z= t + w - x$, weil $z=t+y$ und $y=w-x$
$z \leq t + w \leq t + w + 1 = \frac{w^{2}+w}{2} + w + 1 = \frac{(w+1)^{2} + (w+1)}{2}$
Unter Verwendung von $z \leq \frac{(w+1)^{2} + (w+1)}{2}$ können wir $w$ nach oben abschätzen.
$w = \frac{\sqrt{8t+1}-1}{2} \leq \frac{\sqrt{8z+1}-1}{2} \leq w+1 $
Für $z$ wird $\frac{(w+1)^{2} + (w+1)}{2}$ eingesetzt:
$\frac{\sqrt{8\frac{(w+1)^{2} + (w+1)}{2}+1}-1}{2}$
$\frac{\sqrt{8\frac{w^2+3w+2}{2}+1}-1}{2}$
$\frac{\sqrt{\frac{8w^2+24w+16}{2}+1}-1}{2}$
$\frac{\sqrt{4w^2+12w+9}-1}{2}$ = $\frac{\sqrt{(2w+3)^2}-1}{2}$ = $\frac{2w+2}{2}$ = $\frac{2(w+1)}{2}$ = $w+1$
Um die beiden natürlichen Zahlen x und y aus z zu gewinnen, ist
als erstes $w = \left\lfloor \frac{\sqrt{8z+1}-1}{2} \right\rfloor $ zu berechnen. Dann ergeben sich
$t = \frac{w(w+1)}{2}$ und $y = z -t$ sowie $x = w - y$
Beispiel: Ermittelung von $x$ und $y$ aus $z=\pi(1,3) = 13$
$w = \left\lfloor \frac{\sqrt{8z+1}-1}{2} \right\rfloor = \left\lfloor \frac{\sqrt{8 \cdot 13+1}-1}{2} \right\rfloor = 4.623 = 4 $
$y=13-\frac{w(w+1)}{2} = 13-\frac{4(4+v1)}{2} = 13 - 10 = 3$
$x=w-y = 4 - 3 = 1$
Aufgabe 2
Satz 2: Jede Teilmenge einer abzählbaren Menge ist abzählbar, aber nicht jede Teilmenge einer aufzählbaren Menge ist aufzählbar.
Teilaufgabe 1 - Beweis (Felix Nitsche, Stefan Lüttke)
zu zeigen: Jede Teilmenge $M_2$ einer abzählbaren Menge $M_1$ ist abzählbar. Wenn $M_1$ eine abzählbare Menge ist, dann ist jede Teilmenge $M_2 \subseteq M_1$ abzählbar.
Da für $M_2 = \emptyset$ die Aussage offensichtlich zutrifft kann angenommen werden dass wenigstens ein Element $a \in M_2$ existiert.
Für $M_1$ als abzählbare Menge existiert eine Funktion
$f(x) = n \in M_1$
welche die Menge der natürlichen Zahlen auf $ M_1 $ abbildet.
Dadurch kann man nun für $M_2$ die folgende Funktion angeben:
$
g(x) = \begin{cases}
f(x); & f(x) \in M_2;\\
a; & sonst
\end{cases}
$
Durch diese Funktion wird nun jedem Element der natürlichen Zahlen eindeutig ein Element der Menge $M_2$ zugeordnet, wodurch deren Abzählbarkeit bewiesen ist.
Teilaufgabe 2 - Indirekter Beweis (Max Wielsch, Raik Bieniek)
zu zeigen: Nicht jede Teilmenge $M_2$ einer aufzählbaren Menge $M_1$ ist aufzählbar.
oder: Wenn M1 eine aufzählbare Menge ist, dann gilt nicht für alle Teilmengen $M_2$ ⊆ $M_1$, dass sie aufzählbar sind.
Indirekter Beweis: Behauptung: Wenn $M_1$ aufzählbar, dann jede Teilmenge $M_2$ ⊆ $M_1$ ist aufzählbar.
Gegeben:
- f: ℕ ↦ $M_1$; aufzählbar (surjektiv; berechenbar)
- $M_2$ ⊆ $M_1$
- Satz 1: Wenn $M_2$ entscheidbar ⇔ $M_2$ und $M_1 \setminus M_2$ aufzählbar.
- Satz 2: Wenn $M_2$ aufzählbar → dann ist $M_2$ semientscheidbar.
Gesucht:
- g: ℕ ↦ $M_2$; aufzählbar (surjektiv; berechenbar), d. h. es gilt Satz 1.
$g(x) = \left\{\begin{array}{cc} f(x), wenn\ f(x) ∈ M_2\\ a, wenn f(x) ∈ M1\setminus M_2\\ \end{array}\right. $
laut Satz 2:
$Χ'_{M_2,M_1}(w) = \left\{\begin{array}{cc} wahr, (f(i) = w) ∈ M_2; für\ i\ von\ 0\ bis\ ∞\\ ⊥, sonst\\ \end{array}\right. $
$Χ_{M_2,M_1}(w) = \left\{\begin{array}{cc} wahr, (f(i) = w) ∈ M_2; für\ i\ von\ 0\ bis\ ∞\\ falsch, (f(i) = w) ∈ M_1\setminus M_2 \\ \end{array}\right. $
$Χ'_{M_2,M_1}$ vs. $Χ_{M_2,M_1}$; entscheidbar ☇ semi-entscheidbar. → Behauptung falsch → Satz wahr.
Aufgabe 3
Satz 3: Wenn die Menge $M$ entscheidbar ist, dann ist $M$ aufzählbar.
Beweis:
Es ist gegeben, dass $M$ entscheidbar ist. Damit ist $M$ auch semi-entscheidbar. Wie in Satz 1 bereits bewiesen wurde gilt, dass jede semi-entscheidbare Menge auch aufzählbar ist.
Aufgabe 4
Eine Menge M, mit $M \subseteq A^*$ ist entscheidbar genau dann, wenn M und $A^* \setminus $M aufzählbare Mengen sind.
Teilaufgabe 1 - Beweis Teil 1 (Ingo Körner, Christof Ochmann)
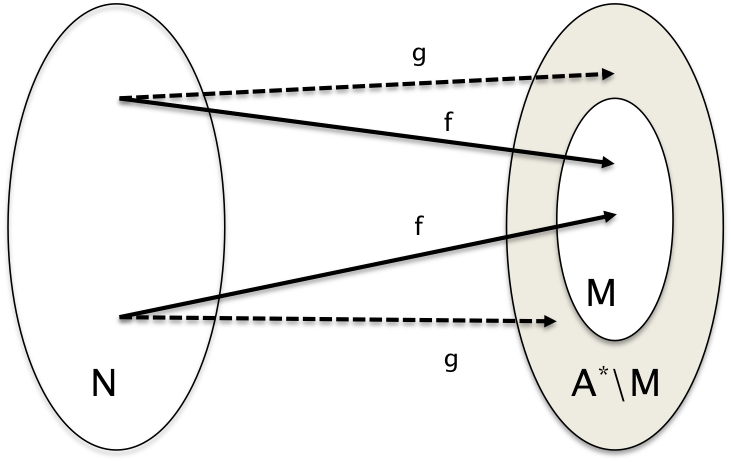
Hinrichtung des Satzes: Wenn M eine entscheidbare Menge ist, dann sind M und $A^*$\M aufzählbare Mengen.
Beweis: Aus der Entscheidbarkeit von M folg semi-Entscheidbarkeit von M und \M. Jede semi-entscheidbare Menge M ist aufzählbar. Es gibt eine Aufzählfunktion f für M und auch die Cantorsche Paarungsfunktion.
$$f(z) = \begin{cases} g(x), & \text{wenn $\chi'_M$(g(x)) = wahr innerhalb von Zeit y};\\ a, & \text{wenn Proz. für $\chi'_M$(g(x)) innerhalb y ohne Ergebnis}.\\ \end{cases}$$ wobei a $\in$ M, wenn $M \neq \emptyset$
$$g(x) = \begin{cases} w, & \text{w $\in$ M};\\ \perp, & \text{sonst}.\\ \end{cases}$$
Teilaufgabe 2 - Beweis Teil 2 (Tobias Salzmann, Ronald Krause)
zu zeigen: Wenn M und $A^*$\M aufzählbare Mengen sind, dann ist M eine entscheidbare Menge.
Da M und $A^*$\M aufzählbare Mengen sind, gibt es total berechenbare surjektive Funktionen für diese.
Für M lautet die Auzählfunktion $f: \N \mapsto M$:
$$f(n) = \begin{cases} f(n), & \text{wenn } f(n) \in M;\\ a, & sonst \end{cases}$$
Hinweis: $a \in M$ .
Für $A^*$\M lautet die Auzählfunktion $g: \N \mapsto A^*$\M:
$$g(n) = \begin{cases} g(n), & \text{wenn } g(n) \in A^*\text{ \M};\\ b, & sonst \end{cases}$$
Hinweis: $b \in A^*$\M .
Beweis
Da der Beweis erbracht werden soll, dass die Menge M entscheidbar ist, so muss eine total berechenbare Funktion $\chi_M$ existieren.
$$\chi_M(w) = \begin{cases} wahr, & \text{wenn } w \in M;\\ falsch, & \text{wenn } w \in A^*\text{ \ M} \end{cases}$$
Des Weiteren sollte es eine Prozedur chi geben, welche für jedes Wort $w$ in endlicher Zeit für ein $i$ mit w = f(i) oder w = g(i) findet.
Da die Schnittmenge von M und $A^*$\M eine leere Menge ist, kann es kein Wort w geben, welches in beiden Mengen vorkommt, sodass genau gesagt werden kann, ob $w$ in der Menge M oder der Menge $A^*$\ M liegt.
$$M \cap (A^*\text{ \ M}) = \empty,\text{ gilt} f(i) = g(j) = w \text{ ausgeschlossen}$$
Das Wort $w$, welches aus der Wortmenge $A^*$ stammt, und die Vereinigung der beiden Mengen, die Wortmenge ist, so muss das Wort $w$ in diesen beiden Mengen liegen. Um die Abzählbarkeit zu gewährleisten, wird abwechselnd das $i$-te-Wort aus $f$ und $g$ gesucht, sodass kein Wort vergessen wird.
$$\chi_M(w) = \begin{cases} wahr, & \text{wenn } f(i) = w;\\ falsch, & \text{wenn } g(i) = w \end{cases}$$
Teilaufgabe 3 - Illustration (Robert Rosenberger, Stefan Scheumann)
Übung 4, Aufgabe 4 (Teilaufgabe 3)
Illustrieren Sie den Beweis (Aufgabe 4.2) durch ein Scheme-Programm.