Aus ProgrammingWiki

Inhaltsverzeichnis 1 Wort-spezifische TM 1.1 Aufgabe 1.2 Lösung 2 Wahrheitstafelmethode für aussagenlogische Äquivalenzen 2.1 Aufgabe 2.2 Lösung 3 Reduktion

Wort-spezifische TM

Aufgabe

Geben Sie sich eine TM vor, die eine selbstgewählte Funktion berechnet, d.h. die angesetzt auf ein Eingabewort das Resultat auf das Band schreibt und den Kopf auf das erste Zeichen von setzt.

Testen Sie diese Maschine ausgiebig. Verwenden Sie AutoEdit aus AtoCC.

Entwickeln Sie anschließend für ein konkretes Wort eine TM aus durch Modifikation der Definition von per Hand. Wenn auf dem (anfangs) leeren Band gestartet wird, soll als erstes auf das Band schreiben und sich anschließend verhalten, wie , sodass = .

Machen Sie sich klar, dass auf diese Weise jedem Wort je eine spezielle TM zugeordnet werden kann.

Lösung

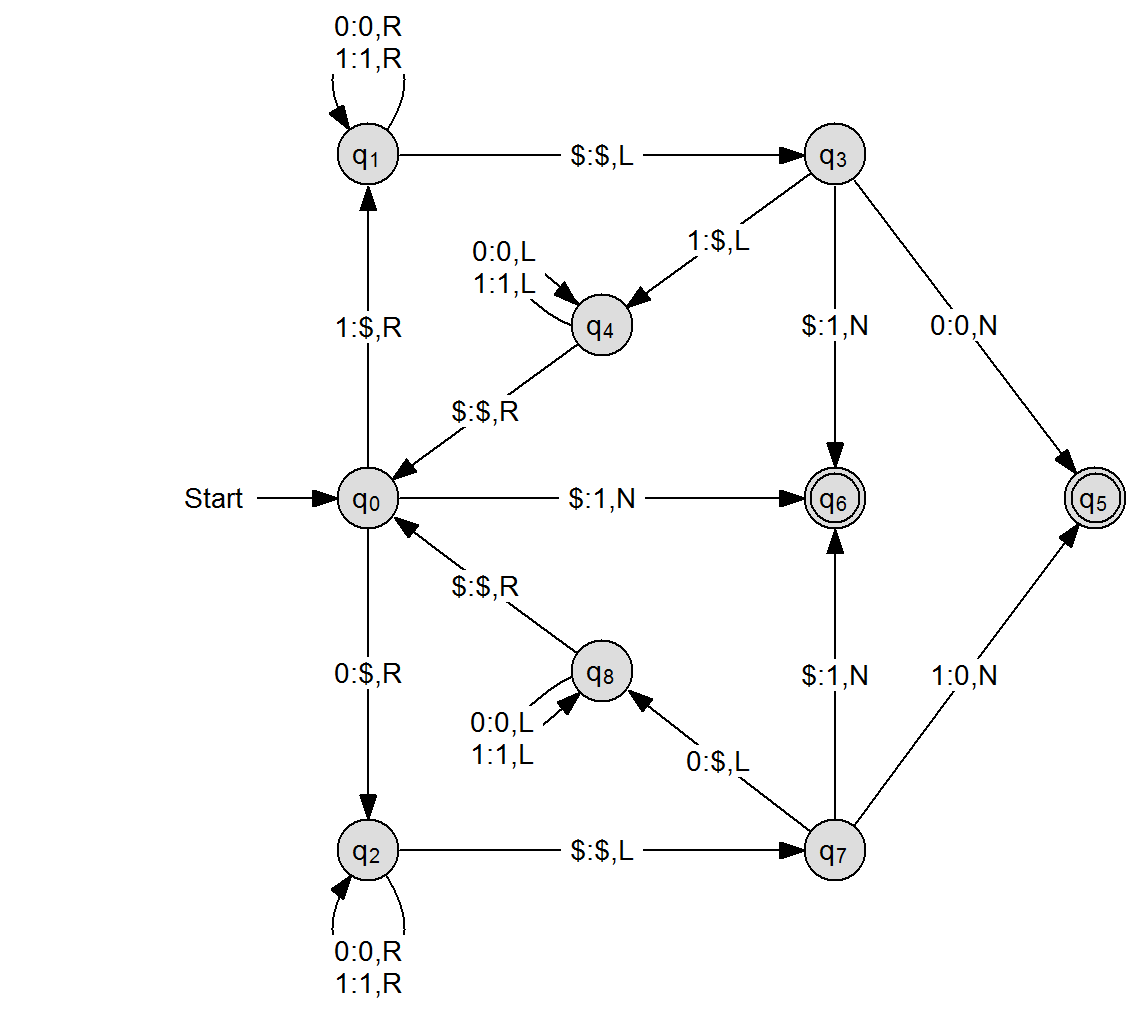
Wir wählen eine Funktion f, die prüft, ob das übergebene Element ein Palindrom ist oder nicht. Dabei legen wir fest, dass die Elemente des Definitionsbereiches im Dualsystem bereitgestellt werden.

Wir haben für diesen ersten Teil der Aufgabe eine Turingmaschine entworfen, die immer in einem Endzustand stoppt. Der Kopf der Maschine steht dann über dem zuvor geschriebenen Zeichen, dem Funtktionswert (0 oder 1).

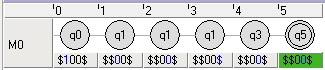
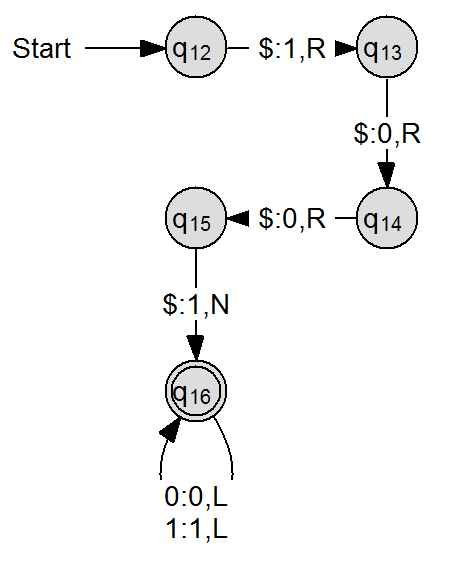
Für den zweiten Teil haben wir als konkretes Wort "1001" festgelegt. Wir haben eine Turingmaschine erzeugt, die die Zeichen auf das Band schreibt und anschließend den Kopf vor das erste Zeichen bewegt.

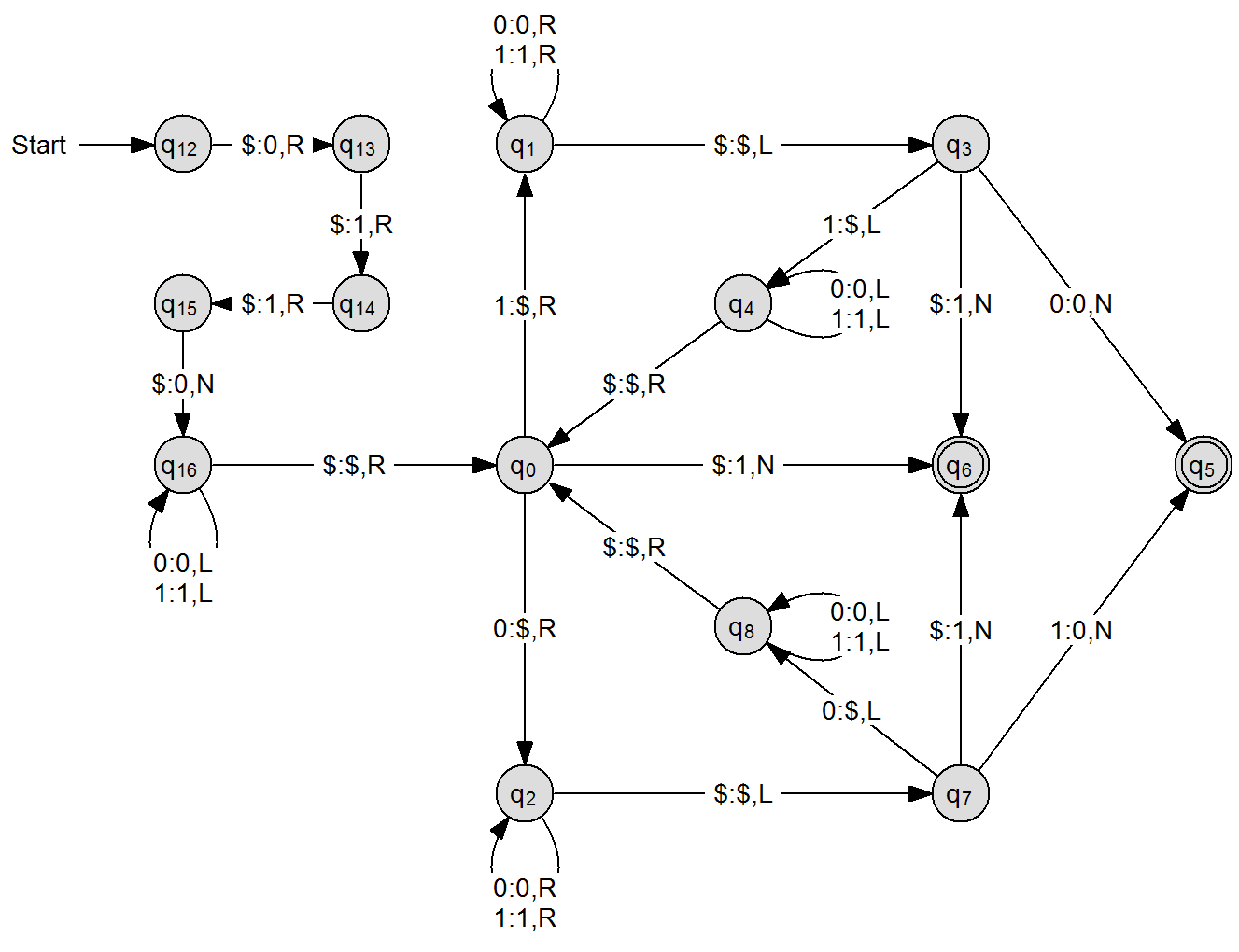
Im letzten Schritt werden die beiden Turingmaschinen miteinander verbunden, sodass eine einzelne Maschine entsteht, die das leere Wort als Eingabe nimmt und sich verhält wie die Maschine aus Teil 1 mit Eingabe von "1001".

Wahrheitstafelmethode für aussagenlogische Äquivalenzen

Aufgabe

Verwenden Sie die Wahrheitstafelmethode, um zu zeigen, dass aus

Wenn und , dann .

folgt

Wenn und , dann .

Lösung

Die Aussagen werden zuerst Variablen zugeordnet. Diese können entweder wahr oder falsch sein.

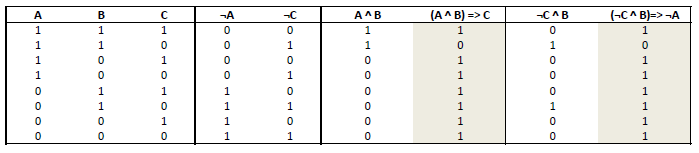
In der folgenden Tabelle sind die Aussagen A, B, C, dargestellt. Die beiden markierten Spalten stehen für die beiden Sätze, welche durch die logische Aussagen entstehen. Man sieht, dass beide Spalten identisch sind, somit ist der Satz von der Aufgabe korrekt.

Reduktion