Aus ProgrammingWiki

Inhaltsverzeichnis 1 Prozedur stoppt-collatz-bis? 1.1 Aufgabenstellung 1.2 Lösung 2 Beweis 2.1 Aufgabenstellung 2.2 Lösung 2.2.1 Definition von 2.2.2 Beweis 3 Turingmaschine (TM) und RADOsche Funktion 3.1 Aufgabenstellung 3.2 Lösung 3.2.1 TM für n=1 3.2.2 TM für n=2 4 Beweis 4.1 Aufgabenstellung 4.2 Lösung 4.3 Zusatz: Aufzählfunktion der Schnittmenge

Prozedur stoppt-collatz-bis?

Aufgabenstellung

Schreiben Sie eine Scheme-Prozedur stoppt-collatz-bis?, die eine Zahl als Eingabe erwartet und feststellt, ob die endlichen Collatzfolgen für existieren.

Lösung

(define collatz (lambda (n) (cond ((= 1 n) (list 1)) ((= (modulo n 2) 0) (cons n (collatz (/ n 2)))) (else (cons n (collatz(+ (* 3 n) 1))))))) (define stoppt-collatz-bis? (lambda (n) (cond ((= n 1) #t) (else (collatz n) (stoppt-collatz-bis? (- n 1))))))

(collatz 7)

ausführen

(stoppt-collatz-bis? 10)

ausführen

Beweis

Aufgabenstellung

Beweisen Sie, dass nicht berechenbar ist, d.h. eine Prozedur totalmacher für , die eine partielle zahlentheoretische Funktion nimmt, gibt es nicht.

Lösung

Definition von

Die Funktion ist definiert als:

mit und . Dabei ist der Wertebereich von .

Beweis

Der Beweis erfolgt durch den indirekten Beweis. Dafür wird die Annahme getroffen, dass berechnbar ist. Dann ist das Prädikat berechenbar. Somit ist haelt_fuer_n? ebenfalls berechenbar. Dies widerspricht jedoch dem HALTEPROBLEM. Damit ist die Annahme falsch, also nicht berechenbar.

Turingmaschine (TM) und RADOsche Funktion

Aufgabenstellung

Machen Sie sich mit dem in AtoCC eingebauten TM-Modell vertraut. Tragen Sie einige TM zusammen, die das Busy-Beaver-Problem für kleinere n lösen. Verwenden Sie AtoCC, um diese zu simulieren.

Lösung

In diesem Wikipedia Artikel ist eine Erläuterung des Busy-Beaver zu finden.

Obwohl die Turing-Maschine ein Produkt der Theoretischen Informatik ist, ist in diesem Video zu sehen, dass dieses Modell nur theoretische Spielerei ist. In dem Video ist eine TM zu sehen, die den Busy Beaver mit 4 Zuständen berechnet.

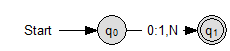
TM für n=1

Definition:

Übergange:

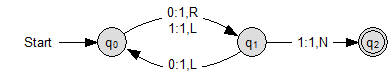
TM für n=2

Definition:

Übergänge:

Beweis

Aufgabenstellung

Zeigen Sie, dass die Vereinigungsmenge zweier aufzählbarer Mengen und wiederum eine aufzählbare Menge ist.

Lösung

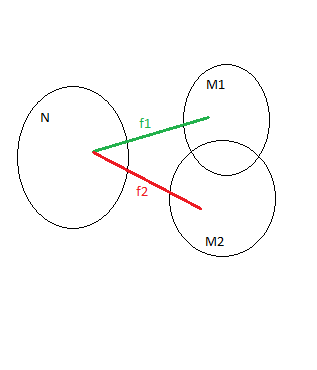
In der Zeichung ist zu erkennen, dass es für eine natürliche Zahl durch Anwendung der Aufzählfunktionen und zwei Abbildungen gibt. Eine Abbildung in und ein in .

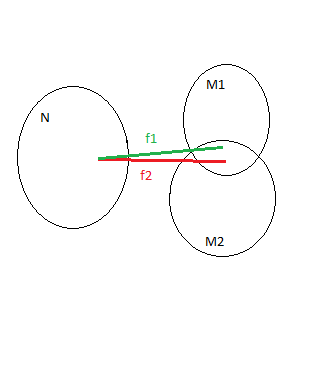
Um nachzuweisen, dass ebenfalls aufzählbar ist, benötigt man eine Funktion , die diese Menge aufzählt. Die Ausgaben dieser Funktion wären folgende:

Es ist zu erkennen, dass die Funktion wie folgend definiert sein muss.

;;; STREAMS - Implementation mit verzoegerter Evaluation (delay, force) ;; als cons aus einem Kopfglied und einem verzögerten Reststream ;; Selektoren (define stream-car car) (define stream-cdr (lambda (stm) (force (cdr stm)))) ;; Konstruktoren (define-syntax stream-cons (syntax-rules () ((_ head tail) (cons head (delay tail))))) ;; Praedikat (define stream? (lambda (stm) (and (pair? stm)(promise? (cdr stm))))) ;; Operationen mit streams (define make-stream (lambda (seed proc) (letrec ((stream-builder (lambda (n) (stream-cons n (stream-builder (proc n)))))) (stream-builder seed)))) (define *the-end-of-stream-tag* (make-stream "eos" (lambda (str) str))) (define stream-item (lambda (str k) (if (= k 0) (stream-car str) (stream-item (stream-cdr str) (- k 1))))) (define stream->list (lambda (str n) (if (<= n 0) '() (cons (stream-car str) (stream->list (stream-cdr str) (- n 1)))))) (define stream-map (lambda (f str) (stream-cons (f (stream-car str)) (stream-map f (stream-cdr str))))) (define print-stream (lambda (stm n) (cond ((<= n 0) (display "...\n")) (else (display (stream-car stm)) (display ", ") (print-stream (stream-cdr stm) (- n 1)))))) (define stream+ (lambda (stm1 stm2) (stream-cons (+ (stream-car stm1) (stream-car stm2)) (stream+ (stream-cdr stm1) (stream-cdr stm2))))) ;--------------------------------------------------------- (define nat-stream (lambda (start) (stream-cons start (nat-stream (+ start 1))))) (define natzahlen (nat-stream 0))

(define f1 (lambda (n) (* n 2))) (define f2 (lambda (n) (+ (* 2 n) 1))) (define g (lambda (n) (cond ((= (modulo n 2) 0) (f1 (/ n 2))) (else (f2 (/ (- n 1) 2)))))) (define gstream (stream-map g natzahlen))

(print-stream gstream 20)

ausführen

Zusatz: Aufzählfunktion der Schnittmenge

Etwas schwieriger wird es, wenn wir beweisen sollen, dass wenn M1 und M2 aufzählbar sind, auch die Schnittmenge von M1 und M2 aufzählbar ist. Dazu muss ebenfalls eine surjektive und berechenbare Funktion g existieren, die unter Verwendung von f1 und f2 die Schnittmenge von M1 und M2 aufzählt.

Hierbei existiert das Problem, dass wir nicht einfach prüfen können, ob ein Element aus M1 auch in M2 enthalten ist. Da dazu alle Elemente untersucht werden müssen, würde die Funktion nicht zum Ende kommen, bevor alle Elemente aufgezählt wurden. Also müssen wir uns wieder der zeitbeschränkten Evaluation bedienen und der Prüfung, ob ein Element in einer der Mengen enthalten ist, nur eine bestimmte Zeit zur Verfügung stellen.

Wir können aber noch einen weiteren Trick verwenden. Indem wir einfach Listen L1 und L2 für die ersten n Elemente jeder Menge erstellen und prüfen, ob f1(n) in L2 oder f2(n) in L1 enthalten ist. Wenn ja, dann wird das entsprechende n-te Element von M1, bzw. M2 zurückgegeben, ansonsten irgendein beliebeiges a, welches in der Schnittmenge von M1 und M2 sicher enthalten ist. Um dieses a zu finden, können wir einfach die Funktion zunächst mit n=0 aufrufen und dann das n solange zu inkrementieren, bis f1(n) in L2 oder f2(n) in L1 enthalten ist und das erste so gefundene Element zurückgeben.

Das führt uns zur folgenden Implementierung:

;Prüft ob ein Element in einer Liste enthalten ist (define n-in-l (lambda (n l) (if (null? l) #f (if (= n (car l)) #t (n-in-l n (cdr l)))))) ;Aufzählfunktion für die Menge M1 (Menge der Quadratzahlen) (define f1 (lambda (n) (* n n))) ;Aufzählfunktion für die Menge M2 (Menge der ungeraden Zahlen) (define f2 (lambda (n) (+ (* 2 n) 1))) ;Liefert alle Elemente der Menge M, die durch die Funktion f aufgezählt wird von f(0) bis f(n) (define get-l (lambda (n f) (if (= 0 n) (list (f 0)) (append (list (f n)) (get-l (- n 1) f))))) ;Aufzählfunktion für die Schnittmenge von M1 und M2 (define g (lambda (n) (let ((l1 (get-l n f1)) (l2 (get-l n f2))) (if (n-in-l (f1 n) l2) (f1 n) (if (n-in-l (f2 n) l1) (f2 n) first-elem)))));a ;Liefert das erste gemeinsame Element der Mengen M1 und M2 ab einer bestimmten natürlichen Zahl n welches für die Aufzählfunktion verwendet wird (define first-elem-from (lambda (n) (let ((l1 (get-l n f1)) (l2 (get-l n f2))) (if (n-in-l (f1 n) l2) (f1 n) (if (n-in-l (f2 n) l1) (f2 n) (first-elem-from (+ n 1))))))) ;Liefert das erste gemeinsame Element der Mengen M1 und M2 (define first-elem (first-elem-from 0))

;Funktionen für die Arbeit mit Streams ;Liefert das erste Element eines Streams (define head car) ;Liefert den Rest-Stream ohne dem ersten Element (define (tail stream) (force (cdr stream))) ;Fügt ein Element einem Stream hinzu (define-syntax cons-stream (syntax-rules () ((cons-stream x y) (cons x (delay y))))) (define (g-starting-from n) (cons-stream (g n) (g-starting-from (+ n 1)))) ;Stream für alle Elemente der Schnittmenge von M1 und M2 (define g-stream (g-starting-from 0)) ;Liefert die ersten n Elemente des Streams s (define (stream-elems s n) (cond ((= n 0) (list (head s))) (else (append (list (head s)) (stream-elems (tail s) (- n 1))))))

Zur Aufzählung verwenden wir auch hier wieder Streams und erwarten natürlich nur ungeraden Quadratzahlen:

;Gibt die ersten 100 Elemente der Schnittmenge von M1 und M2 aus (stream-elems g-stream 100)

ausführen