Aus ProgrammingWiki

Inhaltsverzeichnis 1 Aufzählbarkeit und Entscheidbarkeit 1.1 Aufgabe 1.2 Lösung 1.3 Aufgabe 1.4 Lösung 1.5 Aufgabe 1.6 Lösung 1.7 Aufgabe 1.8 Lösung

Aufzählbarkeit und Entscheidbarkeit

Aufgabe

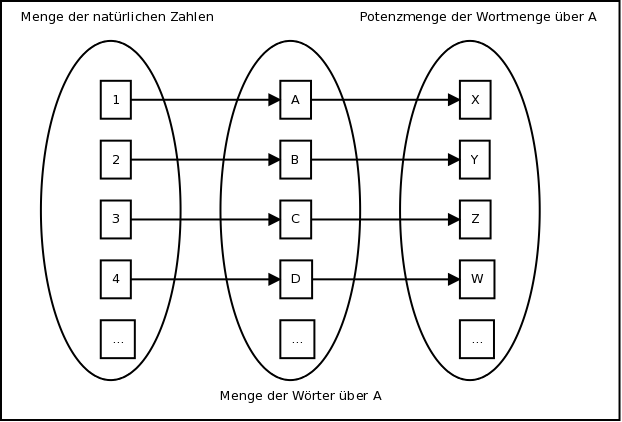
Zeigen Sie, dass für ein beliebiges Alphabet A eine überabzählbar unendliche Menge ist.

Lösung

Wenn abzählbar unendlich wäre, so müsste eine bijektive Abbildung auf die natürlichen Zahlen erfolgen können. Bijektiv bedeutet in diesem Fall, dass jedem Element aus genau ein Element aus zugeordnet wird.

Die Menge wird über gebildet. Unter der Annahme, dass abzählbar unendlich ist, müsste man also zuerst die natürlichen Zahlen auf abbilden können und anschließend auf .

Für eine bijektive Abbildung von auf müssten also alle drei Mengen gleichmächtig, im konkreten Fall also abzählbar unendlich sein. Dass abzählbar unendlich ist steht außer Frage. Dass ebenfalls abzählbar unendlich ist, wurde in Übung 2 nachgewiesen.

Wie kann nun die Mächtigkeit von bestimmt werden? Die Potenzmenge ist folgendermaßen definiert: . Die Menge besteht aus den Wörtern . Daraus folgt, dass für jedes aus ein Element der Form enthält. Zusätzlich enthält aber unter Anderem auch . Das allein reicht aus, um sagen zu können .

Somit ist bewiesen, dass es keine bijektive Abbildung von auf geben kann und somit auch keine von auf . Demzufolge ist eine überabzählbar unendliche Menge.

Aufgabe

Implementieren Sie eine Scheme-Prozedur chi-endlich, die eine natürliche Zahl n und eine Liste L nimmt und entweder #t oder #f zurückgibt, je nachdem ob oder gilt. Stellen Sie für den Entwurf von chi-endlich die erforderlichen Hilfsprozeduren bereit.

Lösung

(define (chi-endlich n ls) (cond [(null? ls) #f] [(= n (car ls)) #t] [else (chi-endlich n (cdr ls))]))

(chi-endlich 5 '(1 19 7 23 6 12))

ausführen

(chi-endlich 5 '(1 19 7 23 5 6 12))

ausführen

Aufgabe

Schreiben Sie eine Scheme-Prozedur, die die Menge der Quadratzahlen aufzählt.

Lösung

Man sagt zählt auf, wenn gilt:

ist eine totale Funktion der Form
ist surjektiv und berechnbar und deren Wertebereich ist

Dabei ist die Menge der Quadratzahlen. Die Funktion muss also eine surjektive Abbildung der natürlichen Zahlen auf die Menge vornehmen und berechenbar sein. Dazu benötigen wir die sogenannte Aufzählfunktion für die Menge der Quadratzahlen.

(define g (lambda (n) (* n n)))

Die Menge erzeugen wir mit Hilfe von Streams.

(define stream-car car) (define stream-cdr (lambda (s) (force (cdr s)))) (define-syntax stream-cons (syntax-rules () ((_ head tail) (cons head (delay tail))))) (define stream? (lambda (s) (and (pair? s)(promise? (cdr s))))) (define make-stream (lambda (seed proc) (letrec ((stream-builder (lambda (n) (stream-cons n (stream-builder (proc n)))))) (stream-builder seed)))) (define *the-end-of-stream-tag* (make-stream "eos" (lambda (str) str))) (define stream-item (lambda (str k) (if (= k 0) (stream-car str) (stream-item (stream-cdr str) (- k 1))))) (define stream->list (lambda (str n) (if (<= n 0) '() (cons (stream-car str) (stream->list (stream-cdr str) (- n 1)))))) (define stream-map (lambda (f s) (stream-cons (f (stream-car s)) (stream-map f (stream-cdr s))))) (define print-stream (lambda (stm n) (cond ((<= n 0) (display "...\n")) (else (display (stream-car stm)) (display ", ") (print-stream (stream-cdr stm) (- n 1)))))) (define nat-stream (lambda (start) (stream-cons start (nat-stream (+ start 1))))) (define natzahlen (nat-stream 0))

(define quad-stream (stream-map g natzahlen))

Damit können wir wie folgt implementieren:

(define f (lambda (n) (if (chi-endlich (g n) (stream->list quad-stream (+ n 1))) (g n) 4)))

(f 5)

ausführen

(f 3.789)

ausführen

Aufgabe

Schreiben Sie eine Scheme-Prozedur, die die Menge der Quadratzahlen relativ zur Menge der natürlichen Zahlen semi-entscheidet.

Hinweis: Implementieren Sie eine Prozedur für die (allgemeingültige) und wenden Sie sie auf die Menge (stream) der natürlichen Zahlen an. Überlegen Sie sich vor dem Aufruf genau, welche Ausgabe Sie erwarten.

Lösung

(define chi-strich (lambda (w m) (if (string=? w (stream-car m)) #t (chi-strich w (stream-cdr m)))))

(define quad-stream2 (stream-map (lambda (i) (number->string i)) quad-stream)) (define natzahlen2 (stream-map (lambda (i) (number->string i)) natzahlen)) (define quadRelZuNat (lambda (i) (if (chi-strich (number->string i) quad-stream2) #t (if (chi-strich (number->string i) natzahlen2) #f 'fehler))))

(quadRelZuNat 4)

ausführen

Vorsich: Der folgende Aufruf stoppt nicht!

(quadRelZuNat 5)

ausführen

Um stoppen zu lassen verwenden wir weiter oben definierte Prozeduren.

(define quadRelZuNat2 (lambda (i) (if (chi-endlich i (stream->list quad-stream (+ i 1))) #t (if (chi-strich (number->string i) natzahlen2) #f 'fehler))))

(quadRelZuNat2 5)

ausführen