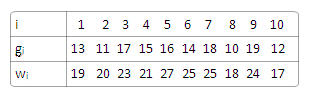AuKAuKAuK43
Aus ProgrammingWiki

Inhaltsverzeichnis |
Lösung des 0/1 Rucksackproblems
Beim Rucksackproblem handelt es sich um ein Optimierungsproblem der Kombinatorik. Aus einer bestimmten Menge von Objekten, die jeweils ein Gewicht und einen Wert haben, soll eine Teilmenge ausgewählt werden, deren Gesamtgewicht ein vorgegebenes Gewichtslimit nicht überschreitet. Hierbei gilt die Optimalitätsbedingung, denn die optimale Gesamtlösung lässt sich aus optimalen Teilproblemen zusammensetzen. Bezogen auf das Rucksackproblem bedeutet das, Gegenstand i wird in den optimal gefüllten, auch leeren, Rucksack gelegt. D.h. alle zur Auswahl stehenden Gegenstände können solange in den Rucksack gelegt werden, solange sie noch Platz haben.
Für den optimal gefüllten Rucksack gilt die rekursive Definition mit:
$i=\text{ Gegenstand }$
$g=\text{ Gewicht }$
$w=\text{ Wert des Gegenstands }$
$n = \text { Anzahl der Gegenstände }$
$K = \text{ Kapazität des Rucksacks }$
$wert(i,g) = \text{ Optimaler Wert für die Gegenstände }$
$wert(n,K)=\text{ Optimaler Gesamtwert }$
$wert(i,g) = \begin{cases} 0, & wenn \ i =0 \\ wert(i-1, g), & wenn \ i > 0 \ und \ g-g_{i} < 0\\ max(wert(i-1,g), wert(i-1, g-g_{i})+w_{i}), & sonst \\ \end{cases}$
Der Fall $wert(i,g) = wert(i-1,g)$ bezieht sich auf einen Gegenstand, der die Restkapazität des Rucksacks überschreiten würde. D.h. $wert(i-1,g)$ ist der Maximalwert aus $1,2,...,i-1$ Gegenständen mit Bezug auf die Kapazität des Rucksacks. Der letzte Fall $wert(i,g) = max(wert(i-1,g), wert(i-1, g-g_{i})+w_{i})$ beschreibt die Maximierung des Wertes in Berücksichtigung des Gewichtes.
Iterativer Algorithmus
Der iterative Lösungsansatz lässt sich, wie bereits erwähnt, nicht mit einer rekursiven Vorschrift umsetzen. Jedoch ist es möglich, die Überlegungen aus dieser Vorschrift zu verwenden und in einen iterativen Lösungsansatz umzuwandeln.
Das soll am folgenden Beispiel demonstriert werden:
| $i$ | 1 | 2 | 3 | 4 | 5 |
| $g_i$ | 2 | 2 | 6 | 5 | 4 |
| $w_i$ | 6 | 3 | 5 | 4 | 6 |
Zur Lösung wird die Gegenstandsliste mit der Prozedur $gegenstaende$ (Quelle: [1], S. 102) auf Vektoren als Gewicht/Wert-Paar abgebildet. Auf das jeweilige Gewicht bzw. den jeweiligen Wert kann dann mittels der Prozeduren $gewicht$ und $wert$ zugegriffen werden. Die Prozedur $gesamtwert-iterativ$ füllt dann eine Tabelle mit den jeweils maximalen Gesamtwerten für die aktuell betrachteten Gegenstände (Zeile) und das darauf bezogene Gesamtgewicht (Spalte). Das Problem hierbei ist die Speicherung aller Werte in der Tabelle, was eine sehr hohe Speicherbelastung nach sich zieht. Für den hier dargestellten Fall genügt es jedoch, wie in der rekursiven Vorschrift notiert, die jeweils letzten beiden Zeilen (zeileAlt und zeileNeu) zu speichern. D.h. die $i$-te Zeile wird aus der $i-1$-ten Zeile berechnet.
Der Aufruf von (gesamtwert-iterativ 5 10) erzeugt folgende Tabelle:
| $n/K$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
| $0$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $1:(g_i=2; w_i=6)$ | 0 | 0 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| $2:(g_i=2; w_i=3)$ | 0 | 0 | 6 | 6 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| $3:(g_i=6; w_i=5)$ | 0 | 0 | 6 | 6 | 9 | 9 | 9 | 9 | 11 | 11 | 14 |
| $4:(g_i=5; w_i=4)$ | 0 | 0 | 6 | 6 | 9 | 9 | 9 | 10 | 11 | 13 | 14 |
| $5:(g_i=4; w_i=6)$ | 0 | 0 | 6 | 6 | 9 | 9 | 12 | 12 | 15 | 15 | 15 |
Rekursiver Algorithmus
Die Lösung des 0/1 Rucksackproblems mittels Rekursion wird im Folgenden mit einer Prozedur gezeigt, die im ersten Teil ohne memoizing und im zweiten Teil mit memoizing arbeitet.
Ohne Memoizing
Als erstes wird die Prozedur (Quelle: [1], S. 106) ohne memoizing implementiert. Die rekursive Definition kann leicht in die Prozedur überführt werden:
Durch die rekursiven Aurufe wird auch die Menge der zu lösenden Teilprobleme bestimmt. Deshalb kommt es in der Prozedur zu Mehrfachberechnungen. Um dies zu verhindern, wird das sogenannte memoizing eingesetzt. Bei dieser Technik wird vor der Berechnung eines neuen Wertes in der Tabelle nachgeschaut, ob dieser Wert bereits vorhanden ist. Wenn er vorhanden ist, wird er verwendet. Ist er nicht vorhanden, wird er berechnet und zur weiteren Verarbeitung in die Tabelle übernommen. Das wird am folgenden Beispiel gezeigt:
Mit Memoizing
Um die rekursive Prozedur (Quelle: [1], S. 107) mit memoizing zu implementieren, benötigt es nur wenige Änderungen im bereits vorhandenen Quellcode.
Als Résumé bleibt festzuhalten, dass die Ergebnisse mit denen der iterativen Prozedur übereinstimmen. Die rekursive Berechnung ohne memoizing ist selbstverständlich nicht tauglich, da durch die unnötige Mehrfachberechnung die Zahl der rekursiven Aufrufe viel zu hoch ist. Der memoizing- Methode wiederum sollte man den Vorzug vor der iterativen Methode geben, denn sie ist mindestens so schnell wie diese, ermöglicht eine direkte Ableitung der rekursiven Regeln und vermeidet die fehleranfällige Transformation in einen iterativen Bottom-up-Algorithmus.
0/1 Rucksackproblem
Die Optimalitätsbedingung ist erfüllt, da der Gegenstand i in den bis dahin optimal gepackten Rucksack, natürlich bisher ohne i, gepackt wird. So erhält man auf jeden Fall einen optimal gepackten Rucksack, der den Gegenstand i enthält. Dadurch werden alle Gegenstände, wenn sie noch hineinpassen, in einen optimal gepackten Rucksack eingepackt.
Für Gesamtwert wert(n, k) des Rucksacks folgende rekursive Beziehung:
Die Bezeichnung wert(n,K) bezeichnet den größtmöglichen Wert des Rucksackinhaltes, wobei man am Anfang die volle Kapazität K zur Verfügung hat. Die Gegenstände werden mit 1, 2, … durchnummeriert. Der Fall wert(i,g) = wert(i-1,g) zeigt an, dass der Gegenstand i nicht in den Rucksack gepackt wurde, da der Gesamtinhalt sonst die verbliebene Kapazität überschritten hätte. Der Maximalwert, der durch die Aufnahme von Gegenständen aus 1, 2, …, i-1 erzielt worden ist, wird mit wert(i-1, g) bezeichnet und berücksichtigt die vorhandene Kapazität. Logischerweise gibt es keinen Wertzuwachs, wenn der Gegenstand i, obwohl er in den Rucksack passen würde, nicht eingepackt wird. Der dritte Fall der Definition beschreibt die Aufnahme von i, die Reduzierung der Restkapazität durch g-gi und die Steigerung des Gesamtwertes durch wi. Dabei wird nicht ausgeschlossen, dass ein höherer Gesamtwert entsteht, wenn man den Gegenstand i, obwohl man ihn hätte einpacken können, nicht einpackt. Deswegen ist die in der Definition angegebene Maximumbestimmung aus wert(i-1,g) und wert(i-1, g-gi)+wi erforderlich. Zunächst verwendet man die traditionelle Form der Implementierung der „Dynamischen Programmierung“, wobei man die rekursiv definierte Funktion wert nicht verwenden darf, aber die Überlegungen, die zu dieser führten.
Die Gegenstände sind absichtlich nicht nach ihrem Gewicht geordnet.
Für die Gegenstandsliste wird ein Vektor verwendet, dessen Komponenten von den Gewicht-Wert-Paaren der Gegenstände gebildet werden. Dabei soll die Nummerierung der Gegenstände wie in der obigen Tabelle bei 1 beginnen. Deswegen belegt man die 0-te Vektorkomponente mit „dummy“.
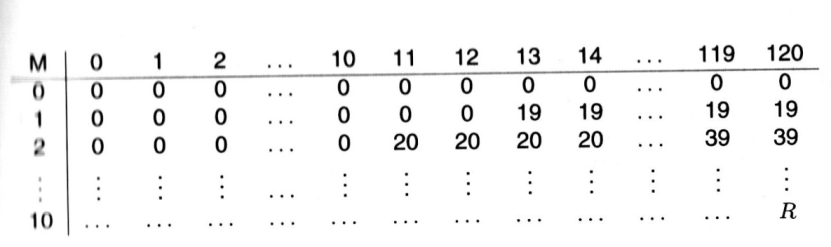
Für die Lösung wird eine Tabelle mit n+1 Zeilen, also für jeden der Gegenstände i = 1, 2, …, n eine und eine zusätzliche Zeile 0 für den Wert des anfänglich leeren Rucksackes, die Initialisierung, sozusagen den Anfangsgesamtwert 0. Die Spaltenköpfe werden von allen möglichen Gewichtssummen von 0 bis K, also im Beispiel von 0 bis 120, gebildet. Der Tabellenkörper enthält jeweils die maximalen Gesamtwerte bezogen auf die bis dahin betrachteten Gegenstände (Zeilen) und das aktuelle Gesamtgewicht (Spalte).
Die rechte untere Ecke der Tabelle (Matrix) zeigt das gesuchte Maximum R = wert(10,120). Eine Implementierung des iterativen Verfahrens mit dieser Matrix ist unnötig speicheraufwändig und da man gemäß der rekursiven Vorschrift (7.1 Seite 101) die i-te Zeile mit Hilfe der i-1-ten Zeile berechnet, reicht es auch, wenn man die letzten beiden Zeilen, in der Prozedur zeilealt und zeileneu, bereithält. Für die Repräsentation in Scheme benutzt man vier Vektoren.
-Wird die Protokollzeile entfernt, gibt die Prozedur einfach nur das Ergebnis, in diesem Fall 183, wider.-
Memoizing
Wir wollen vorerst eine Implementation der rekursiven Formel in einer rekursiven Prozedur ohne memoizing vornehmen, wobei wir die Anzahl der rekursiven Aufrufe ermitteln wollen.
Wir erhalten das Ergebnis von 183, das wir auch schon mit der traditionellen Berechnung ermittelt haben. Die Zahl der zu lösenden Teilprobleme ergibt sich aus der Anzahl der rekursiven Aufrufe und deren Reihenfolge der Bearbeitung wird nun durch den rekursiven Prozess bestimmt.
Wie wir deutlich sehen, sind die 2026 Prozeduraufrufe wesentlich mehr als die 1200 Felder, die man bei der Tabellenvariante zu berechnen hatte. Da manche Elemente der Tabelle scheinbar mehrfach berechnet wurden, wollen wir diese Tatsache durch memoizing vermeiden.
Der Grundgedanke beim memoizing setzt sich daraus zusammen, dass man vor der Berechnung eines Wertes überprüft, ob der Wert, den man ermitteln will, schon vorhanden ist. Trifft dies zu, wird der Wert übernommen. Wenn dem nicht so ist, wird der gesuchte Wert berechnet, gespeichert und für den eventuellen späteren Bedarf gespeichert.
Es kommt zum Einsatz von Assoziationslisten, wenn man die SCHEME-Repräsentation einer Tabelle darstellen will. Ihre Elemente sind als Paare in der Form (key . value) vorzufinden. Zugriff auf einen Wert erhalten wir durch das Sprachelement assoc über den key. Wird der angegebene key gefunden, so erhält man das gesamte Paar zurück. Ansonsten bekommt man den Wert #f ausgegeben.
Wenden wir uns nun der Funktion mit memoization zu. Den Quelltext können wir mit wenigen Veränderungen übernehmen.
Durch die Veränderung des Quelltextes haben wir nun die Technik des memoizing implementiert. Hier nun ein Aufrufbeispiel:
Aus diesem Beispiel lässt sich folgendes erkennen:
- Das Ergebnis (183) stimmt mit den Resultaten überein, die von gesamtwert-iterativ und gesamtwert-rekursiv ermittelt wurden.
- Die Zahl der rekursiven Aufrufe (502) ist gegenüber 2026 deutlich geringer und liegt ebenso deutlich unter 1331 bzw. 1200. Es werden - wie eingangs festgestellt - keineswegs alle Tabellenelemente gebraucht und mir der rekursiven Prozedur auch nicht berechnet.
- Die Länge (501) von Memoliste stimmt beinahe mit der Anzahl rekursiver Aufrufe überein. Der allererste Aufruf kommt hinzu und sorgt somit folglich für die Zahl 502.
Durch die Definition der Variable memoliste in einer Umgebung definiert ist, in welcher der Lambda-Ausdruck zur Definition der Prozedur gesamtwert-iterativ-memo evaluiert wird, bleiben, solange die Prozedur nicht widerholt definiert wird, nach jedem Aufruf erhalten.
Dies führt dazu, dass weitere Aufrufe davon profitieren können und die gegebenenfalls die Liste der bis zu diesem Zeitpunkt berechneten Werte ergänzen. Bei einem wiederholten Aufruf ist keine Neuberechnung nötig, da sich sämtliche Werte bereits in der Memoliste befinden.
Für den Fall, dass der Quellcode nicht richtig evaluiert wird, gibt es hier die Datei zum download: | Simaknoc_Memoizing.zip (0.1 MB) |
Fazit
Beim dynamischen Programmieren ist dem Vorgang der rekursiven Implementation mit memoizing der Vorzug zu geben. Das liegt daran, dass sie mindestens so schnell arbeitet wie das iterative Arbeiten, da sie eine gleiche Aufwandsanordnung besitzen und zudem direkt aus der rekursiven Vorschrift abgeleitet werden kann, wodurch die fehleranfällige Transformation unnötig wird.
__________________________________________________________________________________________________________________________________________________________
Rekursive Berechnung
ohne memoizing
Zunächst wollen wir einen rekursiven Algorithmus ohne memoizing implementieren. Anhand der rekursiven Beschreibung bereitet uns das auch keine Schwierigkeiten und somit kommen wir zu folgender Funktion:
Wie man sehen kann, stimmt das Ergebnis mit dem der iterativen Lösung überein. Jedoch wurden offenbar einige Elemente mehrfach berechnet, da die Zahl der rekursiven Aufrufe deutlich größer ist, als die Anzahl aller Teilprobleme.
mit memoizing
Nun wollen wir den Algorithmus durch memoizing erweitern. Für die Tabelle verwenden wir in Java eine verschachtelte Hashmap der Form HashMap<Integer,HashMap<Integer,Integer>> um schnelle Zugriffe zu gewährleisten. Damit wird die Rechenzeit nicht wesentlich durch das Abfragen der Elemente beeinflusst.
Man kann erkennen, dass wir auch mit memoizing den selben Wert erhalten wie bereits zuvor. Jedoch ist die Zahl der rekursiven Aufrufe deutlich geringer als ohne memoizing und es werden sogar weniger Teilprobleme gelöst als bei der iterativen Variante. Dort mussten ja sämtliche Tabellenelemente, also insgesamt 1331 Teilprobleme berechnet werden. Außerdem sieht man, dass die Länge der memoliste mit der Anzahl der rekursiven Aufrufe nahezu übereinstimmt. Hinzu kommt, dass bei einem erneuten Aufruf, der Algorithmus aus der bereits gefüllten Memoliste einen Vorteil ziehen kann. Da unser Ergebnis ja bereits berechnet wurde, können wir einfach darauf zugreifen und benötigen somit nur einen rekursiven Aufruf, nämlich den ersten.
Fazit
Rekursive Berechnung mit memoizing ist also mindestens genauso schnell wie iterative Berechnung. Lediglich wenn alle Teilprobleme mindestens einmal berechnet werden müssen, ist die iterative Variante gewöhnlich um einen konstanten Faktor schneller wie die rekursive Variante. Dies spielt jedoch kaum eine Rolle, da man diese konstanten Faktoren bei der Aufwandsbetrachtung auch vernachlässigen kann. Zudem werden haufig nicht alle Teilprobleme benötigt und somit sollte die rekursive Variante, die nur die benötigten Teilprobleme berechnet, natürlich bevorzugt werden. Auch schon aus dem Grund, dass diese direkt aus der rekursiven Vorschrift abgeleitet werden kann. Dadurch wird eine fehleranfällige Transformation unnötig.
Rundreiseproblem
Betrachten wir nun die Lösung des Rundreiseproblems unter dem Aspekt der dynamischen Programmierung.
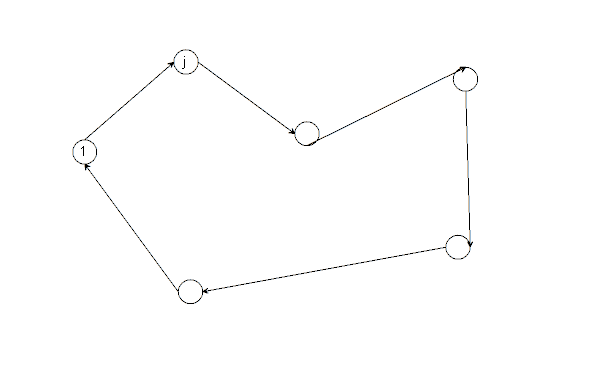
Die Optimalitätsbedingung ist erfüllt, denn es gibt einen minimalen Weg von einer Stadt i = 1 direkt nach Stadt j. Darauf folgen alle Städte aus genau einmal und das Ende ist wieder in 1.
Hierdurch ist rekursive Beschreibung des minimalen Gesamtwegs
offensichtlich.
Die in der Grafik dargestellten "leeren" Orte der Rundreise stellen beliebig viele Orte dar. Der gekennzeichnete Weg ist eine von vielen Möglichkeiten.
Sind bereits alle Städte besucht worden, kehrt man von der aktuellen Stadt i zurück zu 1.
Die Tabelle, die durch die iterative Herangehensweise entsteht, besitzt n Spalten für die Städte 2, 3, 4, ..., n und Zeilen für alle möglichen Städtemengen
Letzteres entspricht der Potenzmenge
.
Daraus folgt, dass die jeweilige Spalte der Tabelle oder Matrix das erste Argument ist und die jewels ausgewählte Zeile das zweite Argument von weg ist. Dies ist zwar entgegen der Gewohnheit, jedoch ist es auch eine Garantie dafür, dass alle zur Berechnung eines Tabellenfeldes gebrauchten Werte entweder in der Entfernungsmatrix oder bereits in der Tabelle stehen. Diese wird bei der traditionellen Berechnung zeilenweise gefüllt.
Die Anzahl der Tabellenfelder beträgt und der zur Berechnung jedes Feldes erforderliche Aufwand liegt - wegen der durch j bestimmten Anzahl von Summen in der Minimumbildung - in
. Somit ergibt sich ein Aufwand in
für das mit dynamischen Programmieren arbeitende Verfahren.
Verglichen ist dieser Aufwand zwar besser als der des naiven Algorithmus , bei dem alle Städte-Permutationen gebildet werden und aus den dazugehörigen Weglängen anschließend die kleinste Zahl gesucht wird.
Der Aufwand ist in beiden Fällen jedoch ein exponentieller, welcher die Lösung des Problems für größere Städtezahlen n praktisch unmöglich macht.