Aus ProgrammingWiki

Autor: Yevgeniy Oliynyk

Flussnetzwerk

Bei einem Flussnetzwerk handelt es sich in der Praxis um Materialflüsse, bei dem ein Material von einer Quelle (Ausgangpunkt) zu einer Senke (Endpunkt) fließt. Der Fluss kann nur in bestimmten Kanälen, im Graph als Kanten dargestellt, entlang fließen. Außerdem können sich Kanäle kreuzen, wodurch mehrere Möglichkeiten für das Material entstehen, zur Senke zu gelangen. Diese Kreuzungen werden als Knoten dargestellt, wobei die Quelle und die Senke auch jeweils einen Knoten darstellen. Ausgehend davon, dass jeder Kanal nur eine begrenzte Kapazität aufweist, gilt es den Fluss optimal zu steuern.

Beispiele für Flussnetze sind Wasserrohrsysteme, das Kabelsystem des Stromnetzwerks und das Straßensystem.

Das Problem des maximalen Flusses versucht herauszufinden, was die maximale Flussrate in einem System ist, um das Material von der Quelle bis zur Senke zu transportieren und wie die Auslastungen der einzelnen Kanäle sind. Dabei muss jedoch sichergestellt sein, dass die Flusserhaltung eingehalten wird.

Definition

Flussnetzwerk

Ein Flussnetzwerk wird durch einen Graph $G = (V,E)$ beschrieben, dessen Kanten gerichtet sind. Jede Kannte $(u,v) \in E$ weißt eine nicht negative Kapazität $c(u,v) \geq 0$ auf. In einem Flussnetzwerk liegt jeder Knoten $v \in V$ auf einem Pfad von der Quelle $s$ zur Senke $t$. Somit ist der Graph zusammenhängend.

Fluss

Ein Fluss in $G$ stellt eine reelwertige Funktion $f : V \times V → \mathbb{R}$ dar, die den Flusswert einer Kante beschreibt. Sie muss drei Bedingungen erfüllen:

• Kapazitätsbeschränkung: Für alle $u,v \in V$ gilt $f(u,v) \leq c(u,v)$.
• Asymmetrie: Für alle $u,v \in V$ gilt $f(u,v) = -f(v,u)$.
• Flusserhaltung: Für alle $u \in V \setminus \{s,t\}$ gilt $$\sum_{v \in V} f(u,v) = 0$$ Anders gesagt: die Menge, die in ein Knoten $v \in V \setminus \{s,t\}$ hineinfließt, muss auch wieder herausfließen.

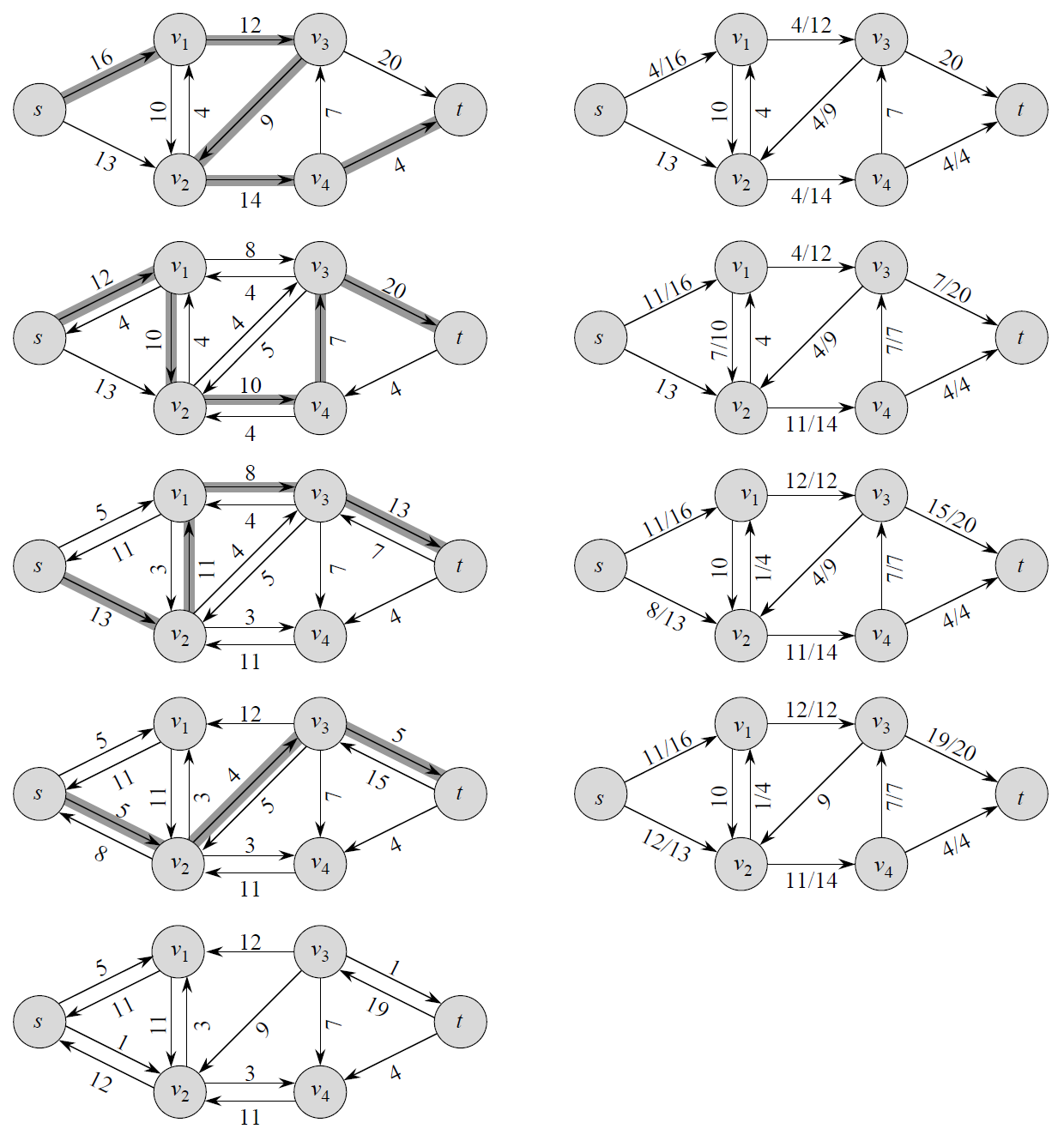
Beispiel

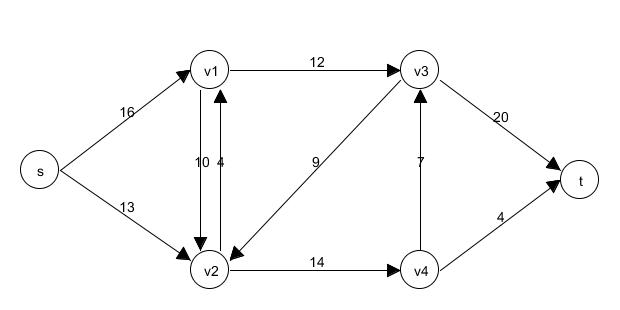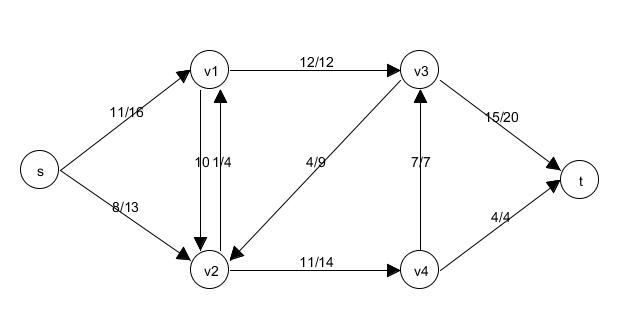Beispiel: Flussnetzwerk	Beispiel: Fluss

Netzwerk mit multiplen Quellen und Senken

Im Fall eines Netzwerks mit mehreren Quellen $\{ s_1,s_2,...,s_m \}$ und/oder Senken $\{ t_1,t_2,...,t_n \}$, werden sogenannte Superquellen bzw. Supersenken eingeführt. Dafür wird von der Superquelle für alle $i = 1,2,...,m$ eine gerichtete Kante $(s,s_1)$ eingefügt. Die Kapazität für diese Kanten ist $c(s,s_i)=\infty$. Genau so wird für alle $i = 1,2,...,n$ die gerichtete Kante $(t_i,t)$ mit der Kapazität $c(t_i,t) = \infty$ eingefügt. Damit wird erreicht, dass jede multiple Quelle mit dem gewünschten Fluss versorgt wird und der Fluss jeder multiplen Senke in die Supersenke münden kann.

Arbeiten mit Flüssen

Implizite Summennotation

Da es verschiedene Funktionen gibt, deren Argumente 2 Knoten sind, wird eine implizite Summennotation verwendet. Beide Argumente können eine Menge von Knoten darstellen. Somit ist es möglich mit Mengen von Knoten zu arbeiten. Seien $X$ und $Y$ Mengen von Knoten, so würde gelten $$f(X,Y) = \sum_{x \in X}\sum_{y \in Y} f(x,y)$$ Die Bedingung zur Flusserhaltung kann nun mit $f(u,V) = 0$ für alle $u \in V \setminus \{s,t\}$ ausgedrückt werden. Ferner wird aus Gründen der Bequemlichkeit auf die geschweiften Klammern verzichtet, womit der Ausdruck $V\setminus s$ in der Gleichung $f(s,V\setminus s) = f(s,V)$ die selbe Bedeutung hat wie $V\setminus\{s\}$.

Lemma

Das Lemma macht gebrauch von der impliziten Summennotation und der Vereinfachung der Differenzmenge.

Dadurch ist es möglich $|f| = f(s,V) = f(V,t)$ zu beweisen. $|f|$ ist der Wert eines Flusses, also z.B. der gesamte Fluss aus der Quelle heraus. Somit sieht der Beweis wie folgt aus:

$$| f | = f (s, V)$$ $$= f (V, V) − f (V \setminus s, V)$$ $$= − f (V \setminus s, V)$$ $$= f (V, V \setminus s)$$ $$= f (V, t) + f (V, V \setminus s,t)$$ $$= f (V, t)$$

Die Ford-Fulkerson-Methode

Diese Methode umfasst verschiedene Implementierungen mit unterschiedlichen Laufzeiten, weshalb sie nur als Methode und nicht als Algorithmus bezeichnet wird. Die Methode setzt sich aus 3 verschiedenen Ideen zusammen, die von Bedeutung sind für viele Flussalgorithmen und -probleme.
Die Methode arbeitet iterativ und beginnt mit $f(u,v)=0$ für alle $u,v \in V$. Durch die Bestimmung eines Erweiterungspfades in jeder Iteration, wird der Flusswert erhöht. Dabei ist ein Erweiterungspfad nichts anderes als ein Pfad von der Quelle zur Senke, der noch über genügend freie Kapazität verfügt, sodass ein größerer Fluss darüber gesendet werden kann. Der Fluss wird dann entlang des Pfades erweitert und der gesamte Prozess wird so oft wiederholt, bis kein Erweiterungspfad mehr vorhanden ist. Als Ergebnis liefert die Methode einen maximalen Fluss.

Ford-Fulkerson-Methode($G$,$s$,$t$)

1  initialisiere den Fluss $f$ mit 0
2  while es existiert ein Erweiterungspfad $p$
3      do verstärke den Fluss $f$ entlang $p$
4  return $f$

Restnetzwerke

Das Restnetzwerk besteht aus den Kanten, die weiteren Fluss aufnehmen können. Das äußert sich bei der Berechnung Restkapazität durch die Formel $$c_f(u,v)=c(u,v)-f(u,v)$$ Sollte $f(u,v)$ negativ sein und beispielsweise $-4$ betragen, so würde sich für $c_f(u,v)$ eine Restkapazität von $c(u,v) + 4$ ergeben und damit wäre die Restkapazität höher als die Kapazität.
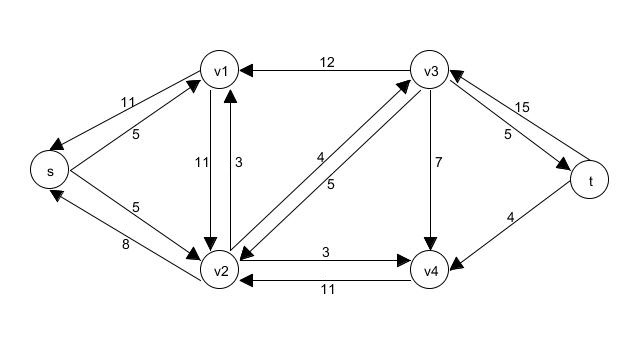
Es lässt sich nun ein Restnetzwerk $G_f=(V,E_f)$ durch $$E_f=\{(u,v)\in V\times V:c_f(u,v) > 0\}$$ für ein vorhandenes Flussnetzwerk $G$ und einen vorhandenen Fluss $f$ angeben. Das bedeutet: Jede Kante von $G_f$ kann einen Fluss aufnehmen, der größer ist als null. Das Restnetzwerk zu dem Flussbeispiel von oben würde so aussehen:

Beispiel: Restnetzwerk

Erweiterungspfade

Ein Erweiterungspfad $p$ ist ein Pfad im Restnetzwerk $G_f$ von $s$ nach $t$ zu einem gegebene Flussnetzwerk $G$ und einem Fluss $f$. Die Definition besagt, dass jede Kante $(u,v)$ eines Erweiterungspfades in der Lage ist einen zusätzlichen positiven Fluss von $u$ nach $v$ aufzunehmen. Dabei wird nicht die Kapazitätsbeschränkung der Kante verletzt. Im Beispiel, dass zuvor ein Restnetzwerk zeigte, ist nun ein Erweiterungspfad blau markiert.

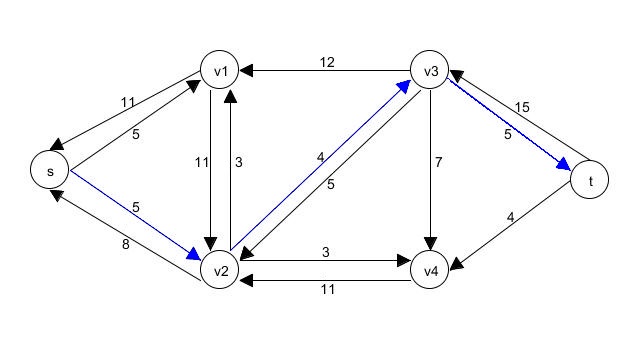
Beispiel: Erweiterungspfad

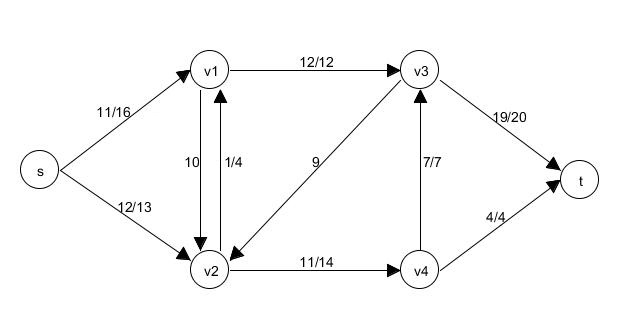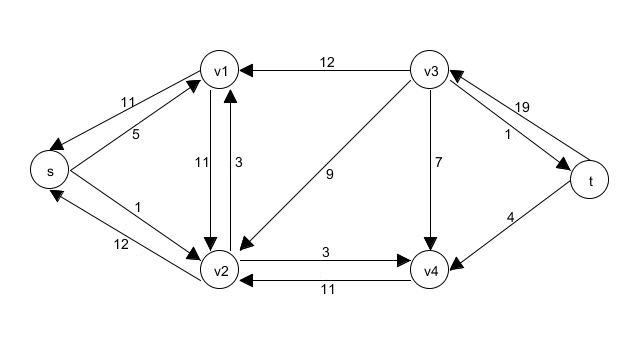Beispiel: Fluss(neu)	Beispiel: Restnetzwerk(neu)

Schnitte von Flussnetzwerken

Um zu zeigen, dass durch die kontinuierliche Erweiterung des Flusses mithilfe von Restnetzwerken und Erweiterungspfaden ein maximaler Fluss entsteht, wird das maximaler-Fluss-minimaler-Schnitt-Theorem angewandt. Das Theorem besagt, dass ein Fluss genau dann maximal ist, sobald keine Erweiterungspfade mehr existieren.

Durch den Schnitt $(S,T)$ eines Flussnetzwerk Partitionierung der Knotenmenge $V$ bewirkt wobei zwei neue Mengen $S$ und $T=V-S$ mit $s\in S$ und $t\in T$ entstehen. Bei der Annahme, dass $f$ ein Fluss ist, definiert sich der Nettofluss durch den Schnitt $(S,T)$ durch $f(S,T)$v und die Kapazität ist in dem Fall $c(S,T)$. Ein Schnitt, das die kleinste Kapazität von allen Schnitten eines Netzwerks darstellt, ist ein minimaler Schnitt.

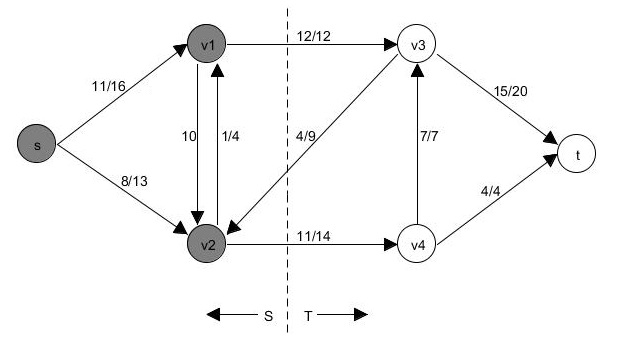Beispiel: Schnitt

Wenn man beachtet, dass $f(S\setminus s, V) = 0$ wegen der Flusserhaltung gilt, kann man das Lemma ähnlich wie schon das vorhergehende Beweisen.

Schaut man sich die Eigenschaften des Schnitts an, so wird deutlich, dass ein Fluss $f$ in einem Flussnetzwerk $G$ nach oben beschränkt ist, und dass durch die Kapazität jedes beliebigen Schnitts. Zur Veranschaulichung: $$|f| = f(S,T)$$ $$=\sum_{u\in S}\sum_{v\in T}f(u,v)$$ $$\leq\sum_{u\in S}\sum_{v\in T}c(u,v)$$ $$=c(S,T)$$ Das Theorem sagt also aus, dass der Wert eines maximalen Flusses offensichtlich gleich der Kapazität eines minimalen Schnitts ist.

Theorem

Der Basisalgorithmus von Ford und Fulkerson

Abarbeitung des Algorithmus am Beispiel (r. Restnetzwerk, l. Fluss)

Jede Iteration der Ford-Fulkerson-Methode liefert einen Erweiterungspfad $p$ und erhöht jede Kante des Pfades den Fluss $f$ um die Restkapazität $c_f(p)$.

Algorithmus

Ford-Fulkerson($G$,$s$,$t$)

1  for alle Kanten $(u,v) \in E[G]$
2      do $f[u,v] ← 0$
3         $f[v,u] ← 0$
4  while es existiert ein Pfad $p$ von $s$ nach $t$ im Restnetzwerk $G_f$
5      do $c_f(p) ←$ min$\{c_f(u,v):(u,v$ gehört zu $p\}$
6         for alle Kanten $(u,v)$ von $p$
7             do $f[u,v] ← f[u,v]+c_f(p)$
8                $f[v,u] ← -f[u,v]$

Als erstes wird ein Fluss mit dem Wert 0 initialisiert (Zeile 1 bis 3). Dann wird solange iteriert, bis kein Erweiterungspfad im Restnetzwerk vorhanden ist (Zeile 4). Wenn ein Pfad gefunden wird, so wird dessen Restkapazität berechnet (Zeile 5) und anschließend der Fluss aktualisiert (Zeile 6 bis 8). Sobald die Bedingung der While-Schleife nicht mehr erfüllt ist, befindet sich in $f$ der maximale Fluss des gegebenen Flussnetzwerks.

Analyse

Die Laufzeit der Prozedur steht in Abhängigkeit mit der Bestimmung des Erweiterungspfades. Eine schlechte Wahl kann unter umständen dazu führen, dass der Algorithmus nicht terminiert und der Wert des Flusses nicht wie gewünscht gegen den Wert des maximalen Flusses konvergiert. Dieser Fall kann jedoch nur dann eintreten, wenn die Kantenkapazitäten irrationale Zahlen sind. Wird der Erweiterungspfad beispielsweise mit Hilfe der Breitensuche bestimmt, läuft der Algorithmus in polynomialer Zeit.
Für die Analyse werden ganzzahlige Kapazitäten vorausgesetzt. Im Falle von rationalen Zahlen, kann eine geeignete Skalentransformation durchgeführt werden. Unter den Bedingungen läuft eine einfacher Implementierung der Prozedur in Zeit $\mathcal{O}(E |f^*|)$. Dabei ist $f^*$ der durch den Algorithmus ermittelte maximale Fluss. Die ersten 3 Zeilen, die Initialisierung, benötigen eine Zeit in $\Theta(E)$. Die While-Schleife benötigt höchstens $|f^*|$ Durchläufe, da sich in jeder Iteration der Wert des Flusses um mindestens eine Einheit erhöht.

Der Edmonds-Karp-Algorithmus

Im Vergleich zum Algorithmus von Ford und Fulkerson, ist dieser Algorithmus besser, was die Schranke angeht. Dabei unterscheiden sie sich nur in der 4. Zeile, denn der Edmonds-Karp-Algorithmus sucht nach einem Erweiterungspfad mit dem Prinzip der Breitensuche. Die Zeit beläuft sich somit in $\mathcal{O}(VE^2)$.

Lösungen

1. Aufgabe

$$f(X,Y ) = \sum_{x\in X} \sum_{y\in Y} f(x,y)$$ $$= \sum_{x\in X} \sum_{y\in Y} -f(y,x)$$ $$= - \sum_{x\in X} \sum_{y\in Y} f(y,x)$$ $$= - \sum_{y\in Y} \sum_{x\in X} f(y,x)$$ $$= - f(Y,X)$$

2. Aufgabe

$$f(S,T) = f (S, V) - f (S, S)$$ $$= f (S, V) $$ $$= f (s, V) + f (S \setminus s, V) $$ $$= f (s, V) $$ $$= | f |$$

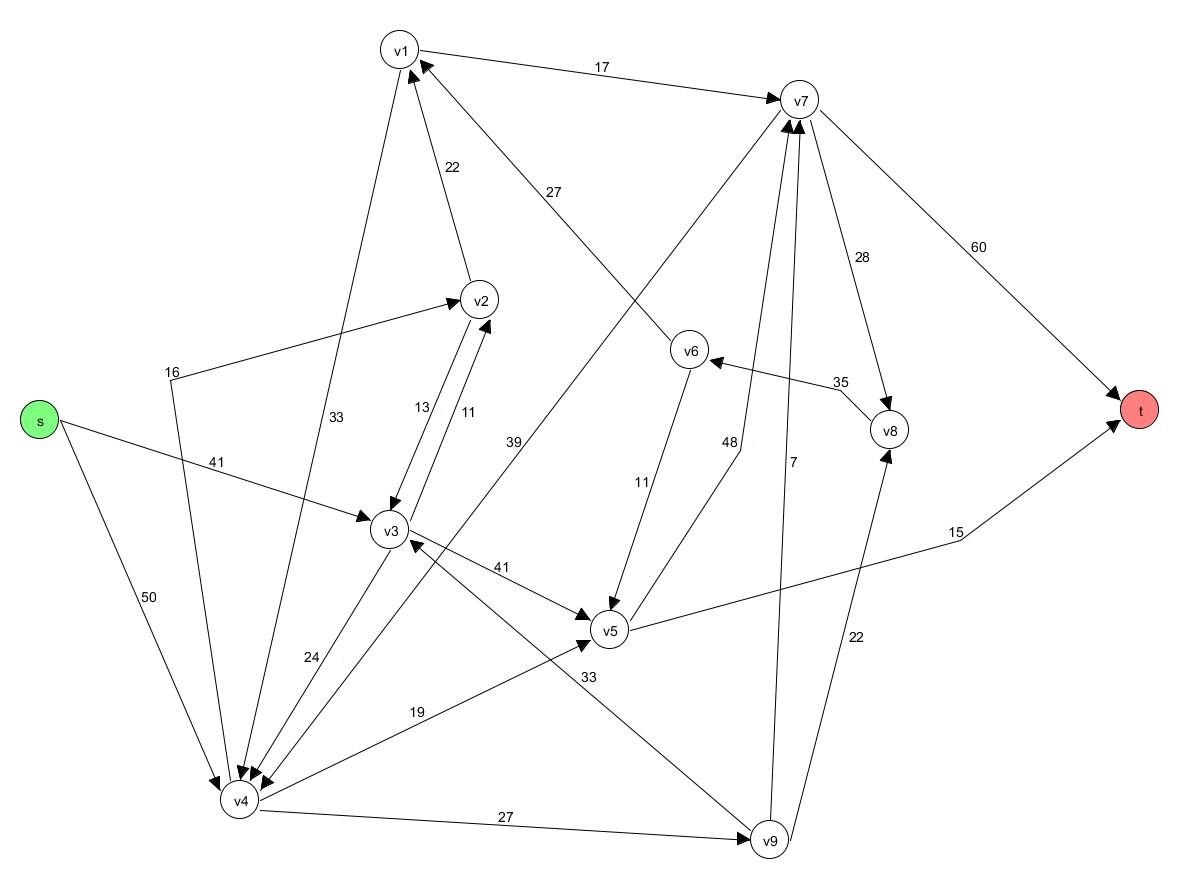
3. Aufgabe

Der Wert des maximalen Flusses beträgt 75. Ein möglicher Fluss wäre:

$f(s,v3) = 38$; $f(s,v4) = 37$; $f(v3,v5) = 38$; $f(v4,v9) = 22$; $f(v4,v5) = 15$; $f(v5,t) = 15$; $f(v5,v7) = 38$; $f(v9,v8) = 22$; $f(v8,v7) = 22$; $f(v7,t) = 60$ (nur positive Flüsse sind angegeben).

Quellen

• Cormen, Thomas; Leiserson, Charles; Rivest, Ronald; Stein, Clifford: Algorithmen, eine Einführung,Oldenbourg Verlag, 2007
• Vöcking, Berthold: Taschenbuch der Algorithmen, Springer-Verlag, 2008
• http://www.informatik.uni-hamburg.de/TGI/lehre/vl/WS1011/AuD/nosec/ad_v15.pdf