Systematische Suche SS11
Aus ProgrammingWiki

- Autoren
- Ronny Lüttke
- Paul Weinhold
Inhaltsverzeichnis |
Rucksackprobleme
Bei den Rucksackproblemen handelt es sich um Optimierungsprobleme. Betrachtet werden dabei nicht-leere Mengen von n Objekten.
Jedes Objekt besitzt dabei zwei Kernattribute:
- einen Wert w
- ein Gewicht g
Als Begrenzung dient ein fest definierter Wert, die Kapazitätsbeschränkung K.
Gesucht ist die Menge derjenigen Objekte, die in der Summe einen maximalen Wert bei bestmöglicher Ausnutzung der Kapazität haben.
Beispiel
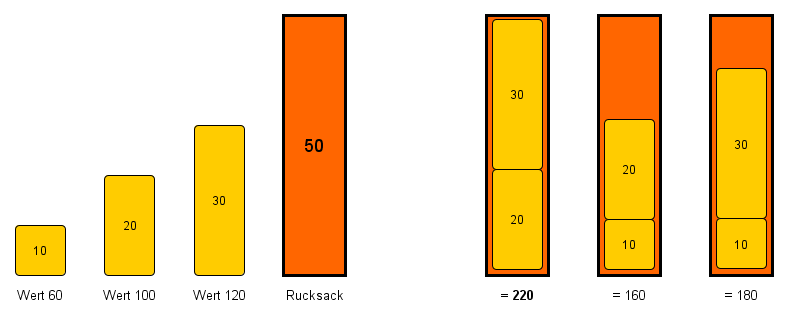
Ein LKW einer Spedition ist bis 50t belastbar. Es müssen einige Container transportiert werden:
- Container 1: Gewicht 10, Wert 60
- Container 2: Gewicht 20, Wert 100
- Container 3: Gewicht 30, Wert 120
Die Objektmenge besteht nun aus den folgenden Wertpaaren:
Die Kapazitätsbeschränkung K ist hier 50
Unterarten
- 0/1-Rucksackproblem (0-1 knapsack problem)
- Ein Objekt darf nur komplett oder gar nicht in die Ergebnismenge übernommen
- Bruchteil-Rucksack-Problem
- Ein beliebiger Teil t (0% ≤ t ≤ 100%) jedes Gegenstands darf übernommen werden
Auf dieser Seite beschränken wir uns auf das 0/1-Rucksackproblem. Bruchteil-Rucksack-Probleme werden bei den Greedy-Algorithmen besprochen.
Ziel
In mathematischer Schreibweise sieht die oben genannte Zielstellung folgendermaßen aus:
Wobei folgendes gelten muss:
, mit
Teilmengen-Summen-Problem (subset-sum-problem)
Hierbei handelt sich um einen Spezialfall des 0/1-Rucksackproblems. Das spezielle ist hier, dass nur eine Menge natürlicher Zahlen gegeben ist:
Gewicht und Wert sind dabei gleich:
, mit
Gesucht ist eine Teilmenge dieser Menge deren Summe diesem Grenzwert möglichst nahe kommt, ihn dabei erreichen, aber nicht überschreiten darf.
Praktisch kann dieser Fall benutzt werden um die maximale Beladung eines LKW zu bekommen, wenn die Güter in Kisten gleicher Abmessung verpackt sind. Das Fahrzeug darf nicht überlastet werden, aber die Kapazität sollte auch möglichst gut ausgenutzt werden.
Intuitives Verfahren
Versucht man den Rucksack intuitiv zu befüllen, würde man wohl zuerst zufällig Gegenstände einpacken. Anschließend tauscht man je zwei Gegenstände aus. Man nimmt einen Gegenstand aus dem Rucksack wieder heraus und legt statt dessen einen höherwertigen zurück. Dabei beachtet man aber, dass die maximale Kapazität nicht überschritten wird. Die Frage ob man auch den maximalen Wert erreicht hat, kann aber nicht wirklich beantwortet werden, da diese Herangehensweise keinerlei System besitzt.
ein anderer Versuch
Man könnte auch annehmen, dass mit einer „gierigen“ Herangehensweise ein optimales Ergebnis erreicht werden kann. Dabei geht immer der noch verbleibende Container mit dem höchsten Wert pro Gewicht in die Ergebnismenge ein, solange die obere Grenze K nicht erreicht wird.
Unter dieser Annahme müsste Container 1 ein Teil der Ergebnismenge sein, da er den größten Quotienten aus Wert und Gewicht besitzt. Die optimale Ergebnismenge enthält Container 2 und 3. Alle Ergebnisse mit Container 1 führen zu einen nicht optimalen Ergebnis, obwohl Container 1 das bessere Verhältnis aus Wert und Gewicht aufweist. Abbildung 1 zeigt deutlich, dass diese Strategie bei 0/1-Rucksackproblemen zu keinem optimalen Ergebnis führt.
Die beiden nachfolgenden Suchstrategien führen stets zu einem optimalen Ergebnis. Es werden jeweils sämtliche Packmöglichkeiten erzeugt und anschließend bewertet. Die maximale Kapazität bleibt dabei vorerst außen vor.
Allerdings können diese Verfahren für große n zu unbeherrschbarem Aufwand führen. Aus diesem Grund werden auch Wege aufgezeigt, den Suchraum noch einzuschränken.
Tiefensuche
Bei der Tiefensuche wird ein Suchbaum aufgebaut. Bäume sind in diesem Fall Gebilde aus der Graphentheorie, welche aus Knoten, Kanten und Blättern bestehen. Ein solcher Baum wird durchlaufen, wobei zunächst zum nächstmöglichen Folgeknoten weitergegangen wird.
Aufbau des Algorithmus
- Bestimmung des Startknotens
- Ersten Knoten expandieren und alle Folgeknoten speichern
- Tiefensuche rekursiv auf jeden gespeicherten Folgeknoten anwenden
- Abbruch:
- bei Fund eines passenden Elements
- wenn kein Knoten mehr im Speicher ist
Erläuterung
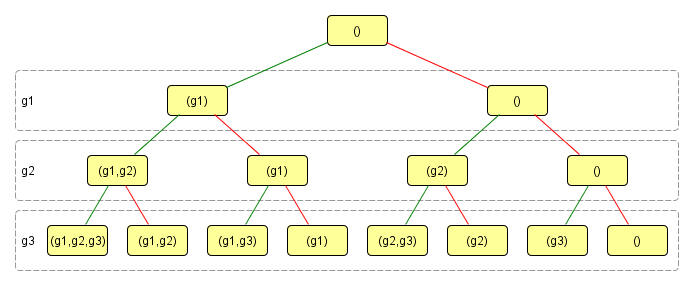
Beim Rucksackproblem entsteht ein Binärbaum, dessen Schichten den einzelnen Objekten zugeordnet werden können. Die Knoten stehen hier für Kombinationen aus Objekten, die Kanten repräsentieren die Entscheidung, ob ein Objekt aufgenommen werden soll (grün) oder nicht (rot). Aufgebaut wird dieser von links her, weshalb man auch von einem dynamischen Baum spricht
Die Suche geht soweit in die Tiefe, bis ein passender Knoten gefunden wird, oder keine Folgeknoten mehr zur Verfügung stehen. In letzterem Fall wird eine Ebene zurück gesprungen und mit dem nächsten Folgeknoten fortgesetzt. Dieses zurückspringen bezeichnet man als Backtracking In der untersten Schicht findet man nun alle möglichen Kombinationen der Objekte wieder, insgesamt also mögliche Kombinationen.
- Herleitung
Vorgehensweisen
Angewandt auf statische Binärbäume erhält man, je nachdem, wann der Inhalt notiert wird 3 verschiedene Vorgehensweisen:
- prewalk: Notation beim ersten Durchgang
- centralwalk: Notation beim zweiten Durchgang
- postwalk: Notation beim dritten Durchgang
Handelt es sich um einen Rechenbaum mit 2-stelligen Operationen, so entsprechen die jeweiligen Ergebnisse der Präfix-, Infix- bzw. Postfix-Notation.
Eigenschaften
Laufzeit
Im schlimmsten Fall müssen alle möglichen Pfade zu allen möglichen Knoten in Betracht gezogen werden. Geht man also davon aus, dass das Überprüfen eines Knotens konstant erfolgt so gilt allgemein , wobei
für die Summe aller Knoten und
für die Summe aller Kanten steht.
Betrachtet man den Binärbaum, der beim Rucksackproblem entsteht ergibt sich die folgende Laufzeitberechnung:
Man erhält also im worst-case eine exponentielle Laufzeit. Für viele Objekte kann eine solche Suche einige Zeit in Anspruch nehmen oder sogar unvertretbar werden.
Vollständigkeit
Allgemein hat die Tiefensuche keinen Anspruch auf Vollständigkeit, da es sich bei dem gegebenen Graphen nicht zwangsläufig um einen Baum handeln muss. Da immer zunächst einmal in die nächste Unterebene gegangen wird, kann es passieren, dass sich der Algorithmus einen Endloszyklus erzeugt, wenn keine Zyklenerkennung eingebaut ist.
Da beim Rucksackproblem aber ein Binärbaum mit fester Tiefe und ohne Zyklen entsteht, kann dieser Fall nicht eintreten.
Optimalität
Dadurch, das die Tiefensuche zunächst die Folgeknoten betrachtet, kann es im allgemeinen Fall passieren, dass ein längerer Pfad gefunden wird, als optimal gewesen wäre. Dieser wird aber im Allgemeinen dafür schneller gefunden.
Bezogen auf das Rucksackproblem ist dies Nebensächlich, da ohnehin alle Möglichkeiten in betracht gezogen werden sollten.
Beispiel der Tiefensuche in Scheme
Breitensuche
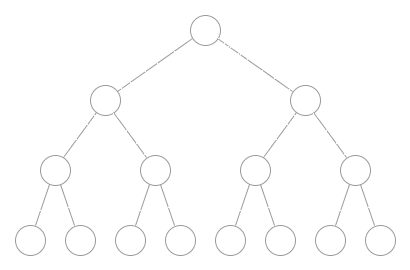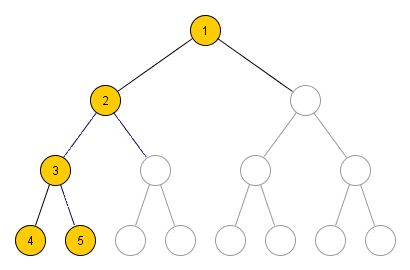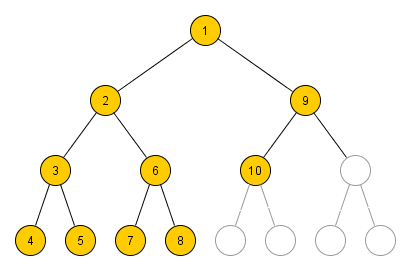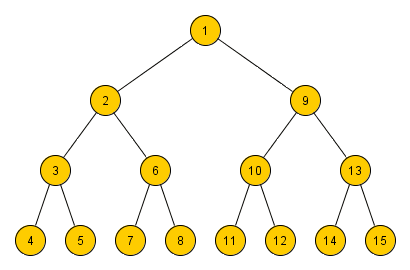
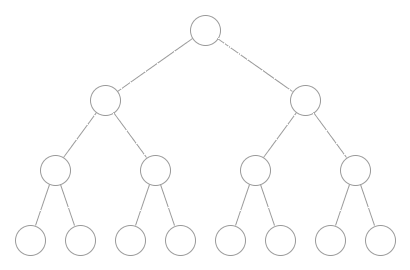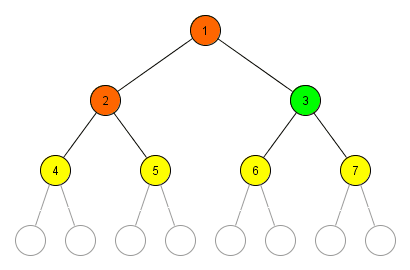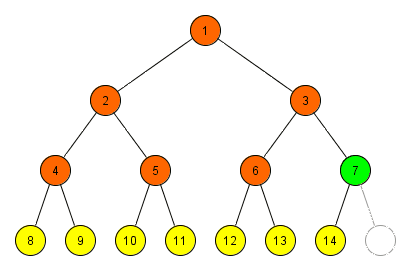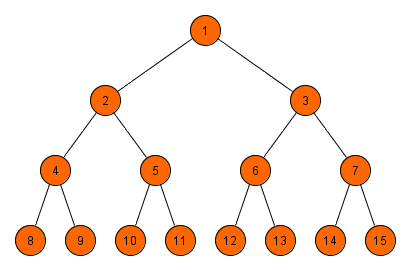
Die Breitensuche durchläuft einen Baum im Gegensatz zur Tiefensuche, nach dem dem Prinzip "Breite zuerst". Dabei wird der Baum schichtweise aufgebaut.
Angewandt auf das Rucksackproblem stellt jede Schicht alle möglichen Kombinationen von n Elementen im Rucksack dar. Jeder Knoten besitzt für n Nicht-Rucksackgegenstände n Teilbäume.
Ablauf des Algorithmus
- Bestimmung des Startknotens
- Alle vom Startknoten erreichbaren Knoten durchlaufen und in die Schlange stellen (Breite zuerst)
- Abbruch: bei leerer Schlange
- Ersten Knoten aus der Schlange entnehmen und damit Schritt 1 wiederholen
Eigenschaften
Laufzeit
Im schlimmsten anzunehmenden Fall müssen, wie in der Tiefensuche, alle Knoten durchlaufen werden. Somit gilt für die Laufzeit auch hier:
Vollständigkeit
Die Breitensuche ist vollständig da alle möglichen Ergebnisse betrachtet werden.
Speicheraufwand
Da das Durchlaufen in jeder Schicht in die Breite erfolgt, müssen im Gegensatz zur Tiefensuche alle Knoten gespeichert werden (Schlange). Dies führt zu einen exponentiellen Speicheraufwand. Daher ist die Breitensuche für umfangreiche Problemstellungen ungeignet.
Aufbau eines Breitensuchbaums
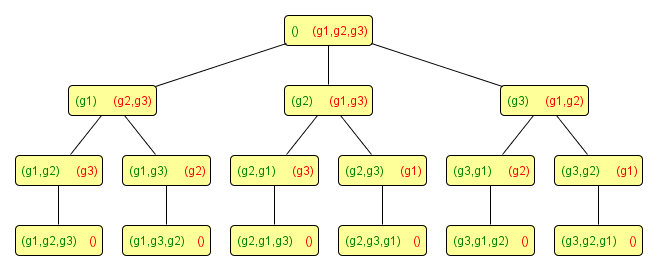
Die Abbildung zeigt den Aufbau eines Breitensuchbaums angewandt auf das Rucksackproblem. Grün dargestellt ist die Menge aller Gegenstände im Rucksack und rot die Nicht-Rucksackgegenstände während eines Knotens
Anzahl der Knoten
Die Anzahl der Knoten ist wie folgt definiert:
Überflüssige Knoten
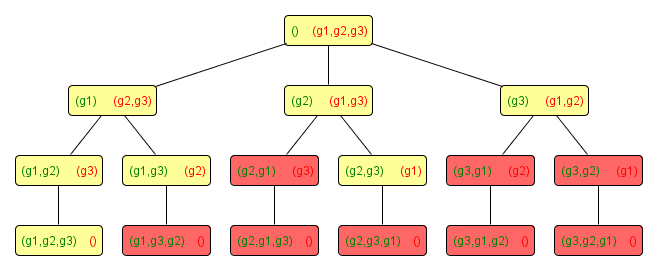

Bei der Betrachtung der Knoten fällt auf, dass für das Rucksackproblem überflüssige Knoten existieren. Für jeden möglichen Rucksack mit n Gegensänden gibt es Knoten, die den gleichen Inhalt repräsentieren. Für das Lösen eines Rucksackproblemes spielt die Reihenfolge der enthaltnenen Gegenstände jedoch keine Rolle. Würde man das Vefahren der Breitensuche in dieser Form für eine große Anzahl von Gegenständen verwenden, so würde es sich schnell als ungeignet erweisen.
Die Gegenstandsliste müsste in der Breitenbewegung reduziert werden um redundante Ergebnisse auszuschließen. Entscheidet man sich für die Aufnahme eines Gegenstandes in den Rucksack, so dürfen die nebenstehenden Knoten der jeweiligen Schicht, diesen nicht mehr in ihrer Gegenstandsliste beinhalten.
Diese Vorgehensweise führt zu einen reduzierten Breitensuchbaum.
Beschränkte und Iterative Tiefensuche
Beschränkte Tiefensuche
Die Beschränkte Tiefensuche arbeitet genau wie die normale Tiefensuche, allerdings mit dem Unterschied, dass eine gegebene Suchtiefe nicht überschritten wird. Auf diese Weise, kann sich diese Art Suche nicht in Zyklen verlieren.
Algorithmus
- Bestimme Startknoten und maximale Suchtiefe
- Prüfe ob aktueller Knoten noch in der Suchtiefe liegt
- Wenn nein: mache nichts
- Wenn ja:
- Merke alle Folgeknoten
- Wende diesen Algorithmus rekursiv auf alle gemerkten Knoten an
Eigenschaften
- Laufzeit: genau wie bei der normalen Tiefensuche,
- Vollständigkeit: nicht gegeben, der Algorithmus kann eventuelle Kandidaten nicht finden, wenn die Suchtiefe zu gering ist.
- Optimalität: nicht gegeben, da sie immer noch so lange einem Pfad folgt wie es die Suchtiefe zulässt
Iterative Tiefensuche
Bei der iterativen Tiefensuche handelt es sich um einen Algorithmus, der die beschränkte Tiefensuche anwendet. Pro Iterationsschritt wird dabei die Suchtiefe um 1 erhöht. Auf diese Weise wird die Schnelligkeit der Tiefensuche mit der Optimalität der Breitensuche kombiniert. Trotz allem ist der Algorithmus langsamer als die normale Tiefensuche, da auch die bereits durchlaufenen Knoten in jedem neuen Iterationsschritt erneut durchlaufen werden müssen.
Algorithmus
- Bestimme Startknoten
- Rufe beschränkte Tiefensuche mit aktueller Suchtiefe auf
- Erhöhe Suchtiefe um 1 und gehe zu Schritt 2
Eigenschaften
- Laufzeit: genau wie bei der normalen Tiefensuche,
- Vollständigkeit: gegeben, der Algorithmus kann sich nicht mehr in Zyklen verlieren
- Optimalität: gegeben durch die Schrittweise Erhöhung der Suchtiefe
Backtracking
Eine besondere Anwendung findet dieser Algorithmus bei einer klassischen Problemstellung:
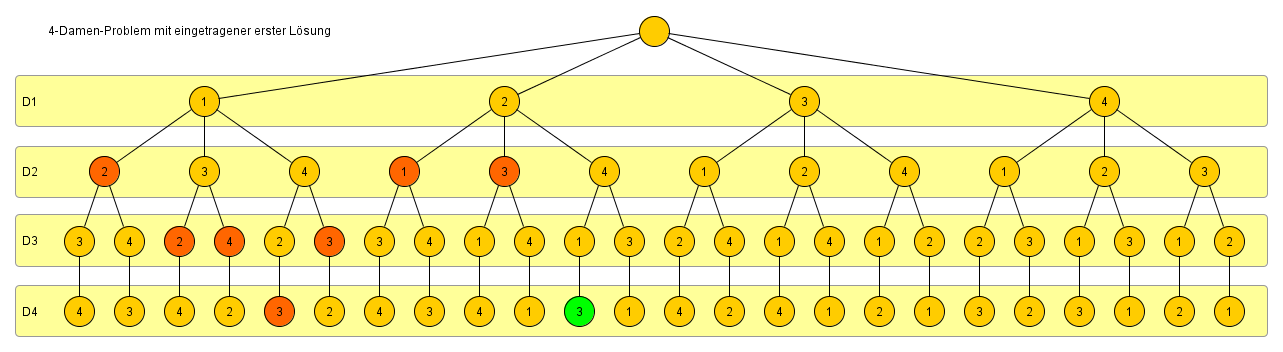
Finde alle möglichen Positionen für n Damen auf einem n mal n großen Schachbrett, ohne dass die Damen sich gegenseitig schlagen können.
Algorithmus
Bei diesem problem entsteht ein Suchbaum mit n Ebenen, wobei nicht jede Kombination zur Lösung führt. Man sucht einfach solange in die Tiefe, bis entweder ein verbotener Zustand auftritt oder ein gewünschtes Ergebnis.
Die folgende Tabelle zeigt die Anzahl der Möglichen Positionen für einige gegebene n auf. Eindeutige Kombinationen, sind dabei solche, die nicht auch durch Drehung und/oder Spiegelung entstehen können.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| eindeutig | 1 | 0 | 0 | 1 | 2 | 1 | 6 | 12 | 46 | 92 | 341 | 1.787 | 9.233 | 45.752 | 285.053 | 1.846.955 | 11.977.939 | 83.263.591 |
| insgesamt | 1 | 0 | 0 | 2 | 10 | 4 | 40 | 92 | 352 | 724 | 2.680 | 14.200 | 73.712 | 365.596 | 2.279.184 | 14.772.512 | 95.815.104 | 666.090.624 |
Beschränkung des Suchbaumes
Reduzieren der Durchlauftiefe
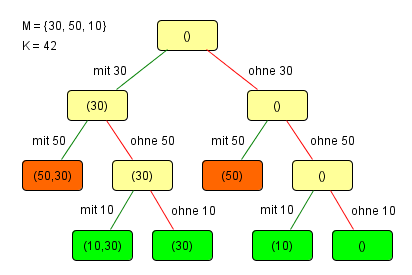
Bislang wurde die Kapazitätsbegrenzung komplett außer Acht gelassen. Um den Suchbaum weiter eingrenzen zu können werden wird eine entsprechende Bedingung in die Prozedur rucksack1 eingebaut, die das bewerkstelligt. Die Hilfs-Prozedur in-max? vergleicht hierbei die Summe der in einer Liste enthaltenen Elemente mit einem Wert.
Die Grafik rechts, als auch das Ausführungsprotokoll (bei aktiviertem tracing) zeigen, dass nur noch 4 Kombinationen als Ergebnis übrig bleiben:
- (10,30)
- (30)
- (10)
- ()
Maximale Wertbestimmung
Nur die Knoten durchzugehen, die noch in die Kapazität passen spart gegebenenfalls einiges an Rechenzeit. Nun interessieren wir uns aber noch für die wertvollste Kombination.
für soll dann also gelten
. Die procedur rucksack2 muss also abermals modifiziert werden:
Der Kern von rucksack2 wird hier in eine Reihe von Umgebungen eingebettet, die sicherstellen, dass immer der maximale Wert mitgeführt wird. Entfernt man das Semikolon in Zeile 5, so wird ein komplettes Ablaufprotokoll ausgegeben.
Nichtdeterminismus
Zur Lösung des Rucksackproblems haben wir Baumstrukturen betrachtet, deren Durchlauf auf unterschiedliche Weisen algorithmiert werden können. Doch nur selten handelt es sich bei diesen Bäumen um explizite Datenstrukturen. Vielmehr kann man sich jene als strukurierte Darstellungsformen vorstellen, die den eigendlichen Ablauf eines Prozesses für einen Menschen sichtbar oder besser vorstellbar machen. Besonders schwierig stellt sich die Findung einer Lösung für komplexe, vielleicht sogar mit Rekursion schwer realisierbare, Probleme. Vielleicht soll die Lösung dieses Problems gar nicht im Vordergrund stehen, sondern vielmehr darauf aufbauend andere Probleme lösbar werden. Das Ziel wäre es doch dem Computer zu beschreiben was zum Beispiel gesucht werden sollte. Deskriptive Programmierung setzt genau an dieser Stelle an.
Ein nichtdeterministischer Algorithmus ist in der Lage auf eine Eingabe mit einer, keiner oder mehreren möglichen Ergebnissen zu antworten bzw. "das Richtige vorherzusehen". Dabei wird im Gegensatz zum Determinismus keine Vorgabe gemacht welche Möglichkeiten das "richtige" Ergebnis darstellen.
Auch wenn die Mittel des Nichtdeterminismus es vielleicht vermuten lassen, bedient sich der Computer bei der Lösungsfindung nicht überirdischer Fähigkeiten. Im Hintergrund findet vielmehr auch eine systematische Suche statt, mit eventuell exponentiellen Aufwand. Zwar bringt die Verwendung von Nichtdeterminismus keine Laufzeitverbesserung, vielmehr wird eine Verbesserung der kognitiven Effizienz erreicht. Der Algorithmus wird somit leichter lesbar, da er auf menschenfreundlichere Art und Weise beschrieben wird.
Implementation in Scheme
Um die Konzepte des Nichtdeterminismus in Scheme nutzen zu können, müssen bestimmte Sprachelemente implementiert werden. Im Folgenden werden kurz fünf Prozeduren vorgestellt, die in Scheme durch Laden der Datei ambiguos.ss zur Verfügung stehen.
- choice: nimmt eine Liste und gibt daraus "das richtige Element" zurück. Durch Einbettung in dieses Sprachelements in einen größeren Ausdruck, kann das "richtig Ergebnis" problemspezifisch "beschrieben" werden.
- bag-of: nimmt eine Liste und gibt daraus eine Liste mit "richtigen Elementen" zurück
- initialize-amb-fail: ist eine nullstellige Prozedur für die Initialisierung des Ambiguous-System
- multichoice: nimmt eine Liste ls und eine natürliche Zahl n und gibt aus ls genau n "richtige" Elemente
- randomchoice: nimmt eine natürliche Zahl n und gibt "das richtige Element" aus einer Liste '(1 2 3 ... n)
Nichtdeterministische Summandensuche
Das folgende Beispiel zeigt die nichtdeterministischen Suche nach passenden Summanden für eine Zahl.
Rucksackproblem
Auch das Rucksackproblem lässt sich beschreiben.
Fazit
Der Vorteil der Tiefensuche kommt vor allem bei Fragestellung wie "Gibt es ein Element, dass eine bestimmte Bedingung erfüllt?" zum tragen, da ein Ergebnis recht schnell gefunden wird. Geht es aber darum möglichst alle Möglichkeiten in Betracht zu ziehen, so liefert die Breitensuche zufriedenstellendere Ergebnisse.
Die Iterative Tiefensuche kombiniert beide Varianten um die Stärken beider Suchalgorithmen nutzbar zu machen.
Jedoch egal welchen Algorithmus man letztendlich wählt, die Laufzeit bleibt im worst-case bei , da schlimmstenfalls wirklich alle Knoten durchgegangen werden müssen.
Scheinbare Vereinfachungen wie der Nichtdeterminismus bringen auch nicht wirklich Performance-Schübe da die eigentliche Funktionsweise lediglich durch Abstraktion verdeckt wird. Die Lesbarkeit des Quelltextes, wird durch diese Hilfsmittel allerdings vereinfacht.
Übungen
Zu den Übungen (gegebenenfalls Rechtsklick>in neuem Tab/Fenster öffnen)
Quellen
Literatur
- Christian Wagenknecht
- Algorithmen und Komplexität.- Fachbuchverlag Leipzig, 2003. - ISBN 3-446-22314-2
- Thomas H. Cormen, Charles E. Leiserson, Ronald Rivest, Clifford Stein
- Algorithmen - Eine Einführung, Oldenbourg Verlag München Wien, 2. Auflage, 2007. - ISBN 978-3-486-58262-8
- Jochen Ziegenbalg
- Algorithmen - Von Hammurapi bis Gödel, Spektrum Akademischer Verlag Heidelberg Berlin Oxford, 1996. - ISBN 3-8274-0114-3
- Markus von Rimscha
- Algorithmen kompakt und verständlich, Vieweg + Teubner Verlag Wiesbaden, 2008. - ISBN 978-3-8348-0569-0
Websites
Wikipedia:Beschränkte Tiefensuche
Wikipedia:Iterative Tiefensuche