Sortierte Folgen WS13-14
Aus ProgrammingWiki

- Autoren
- Dominik Bitterlich
- Alexander Häse
Inhaltsverzeichnis |
Einleitung
Sortierte Folgen
In der Informatik ist eine Folge eine Aneinanderreihung von Symbolen einer Grundmenge. Eine Grundmenge ist eine endliche Menge von voneinander unterscheidbaren Symbolen, die aus Zeichen oder Buchstaben bestehen. Diese können mit Hilfe bestimmter Algorithmen sortiert werden. Bekannte Sortieralgorithmen sind Selection Sort, Insertion Sort, Quicksort, Countingsort und Heapsort. Die neu entstandene Folge nennt man "Sortierte Folge". Diese Folgen können in der Informatik zum Beispiel in Arrays oder Listen umgesetzt werden.
Insbesondere bei einer sortierten Liste sind die Knoten nicht in der sequentiellen Reihenfolge ihrer Eingabe angeordnet, sondern werden nach bestimmten Sortierkriterien (z.B. aufsteigend oder absteigend) geordnet. Sortierte Listen haben Vorteile gegenüber unsortierten Listen – Daten können schneller aufgefunden werden – dies gilt insbesondere für beidseitig verkettete Listen. Denn es kann schon vor Beginn des Suchvorgangs ermittelt werden, ob das gesuchte Element eher am Ende oder am Anfang der Liste zu finden sein wird. Entsprechend kann der Suchvorgang am Ende oder am Anfang der Liste begonnen werden, was die Suchzeit erheblich verkürzt.
Suchen in einer sortierten Folge
Algorithmisches Problem
Bei der Suche in einer sortierten Folge ist es das Ziel ein bestimmtes Element $k$ in einer Menge $M$ zu finden und z.B. dessen Index auszugeben. Eingegeben werden soll eine endliche, aufsteigend sortierte Folge $e_0, e_1 \dots e_n$ von Elementen aus einer Menge $M$, auf der eine Ordnung “$<$” gegeben ist. Außerdem soll ein Element $k ∈ M$, welches gesucht werden soll, angeben werden. Ausgeben werden soll der Index $i$ des Elementes, mit $i ∈ {0, 1 \dots n}$, sodass $e_i = k$ gilt, vorausgesetzt ein solcher Index existiert. Ansonsten wird „nicht enthalten“ ausgegeben.
Beispiele
Beispiel 1:
$M$ sei die Menge der ganzen Zahlen und die gegebene Ordnung “$<$” auf $M$ ist die übliche größer/kleiner Beziehung zwischen zwei ganzen Zahlen.
- Die gegebene, aufsteigend sortierte Folge sei: $5; 7; 9; 10; 14; 16; 17; 22; 36; 48; 52; 127; 212$
- Gesucht werden soll nach $k = 36$.
- Die gewünschte Ausgabe ist der Index $8$.
- Die gegebene, aufsteigend sortierte Folge sei: $5; 7; 9; 10; 14; 16; 17; 22; 36; 48; 52; 127; 212$
- Gesucht werden soll nach $k = 18$.
- Die gewünschte Ausgabe ist nicht enthalten.
Beispiel 2:
$M$ sei die Menge der Wörter der deutschen Sprache und die gegebene Ordnung “$<$” auf $M$ ist die Reihenfolge, in der die Wörter im Duden erscheinen, auch lexikographische Ordnung genannt.
- Die gegebene, aufsteigend sortierte Folge sei: $ambitioniert, bunt, blau, elastisch, gesund, japanisch, jung, verlogen$
- Gesucht werden soll nach $k = krank$.
- Die gewünschte Ausgabe ist nicht enthalten.
Lineare Suche
Lineare Suche ist ein Algorithmus, der auch unter dem Namen sequentielle Suche bekannt ist. Er gehört zu den einfachsten Suchalgorithmen. Die Aufgabe besteht hier darin, ein Element in einer Liste oder einem Array mit $n$ Elementen zu finden.
Die Arbeitsweise ist die folgende:
- 1. Gehe die Indizes $i$ der Elemente in der gegebenen sortierten Folge beginnend bei $0$ einen nach dem anderen durch.
- 1.1 Falls $e_i=k$ ist, dann brich die Suche ab und gib den Index $i$ aus.
- 1.2 Sonst
- 1.2.1 Falls $k < e_i$ ist, dann brich die Suche ab und gib nicht enthalten aus.
- 1.2.2 Sonst gehe zum nächsten Element in der Folge.
- 2. Falls die Suche nicht zwischendurch abgebrochen wurde, gib nicht enthalten aus.
Umsetzen kann man den Algorithmus nun mittels eines Array's oder mittels einer verketteten Liste.
Umsetzung in Java mittels Array
Umsetzung in Java mittels verketteter Liste
Analyse der linearen Suche
Die Analyse dieses Algorithmus im Rahmen dieser Vorlesung wird aus zwei Schritten bestehen:
- 1. Es ist zu zeigen, dass dieser Algorithmus für alle zulässigen Eingaben das gewünschte leistet.
- 2. Es ist abzuschätzen, wie lange der Algorithmus im schlechtesten Fall, dem sogenannten worst case scenario, braucht.
Dass die lineare Suche das gewünschte leistet, ist intuitiv plausibel. Also wird sich im Folgenden eingehend mit der Laufzeit des Algorithmus beschäftigt.
Annahmen zur Analyse der Laufzeit
Es wird angenommen, dass die Ausführung folgender Bausteine eines Algorithmus, die nicht von der Eingabe abhängen, auf jedem Rechner nach einer bestimmten Zeit abgeschlossen ist:
- Vergleich
- Zuweisung eines Wertes an eine Variable
- Addition von zwei ganzen Zahlen
- Rückgabe eines Wertes aus einer Methode
Außerdem wird festgehalten, dass die Anweisungen/Befehle in konstanter Zeit ausgeführt werden können und sie werden als elementare Anweisungen/Befehle bezeichnet.
Laufzeit in Abhängigkeit von der Eingabe
Eine Analyse der Laufzeit eines Algorithmus bedeutet also im Wesentlichen zu zählen, wie viele elementare Anweisungen insgesamt im Algorithmus ausgeführt werden. Allerdings wird diese Anzahl in den meisten Fällen davon abhängen, welche Eingabe dem Algorithmus übergeben wurde.
Beispiele:
Der Einfachheit halber zählen wir erst einmal nur die Vergleiche, die zwischen $k$ und den Elementen aus $M$ in der gegebenen Folge durchgeführt werden.
- Folge: $5; 7; 9; 10; 14; 16; 17; 22; 36; 48; 52; 127; 212$
- $k = 9$
- Die Anzahl der Vergleiche beträgt $5$: zwei Mal mit $4$, zwei Mal mit $7$, ein Mal mit $9$.
- Folge: $5; 7; 9; 10; 14; 16; 17; 22; 36; 48; 52; 127; 212$
- $k = 8$
- Die Anzahl der Vergleiche beträgt $6$: zwei Mal mit $4$, zwei Mal mit $7$, zwei Mal mit $9$.
- Folge: $5; 7; 9; 10; 14; 16; 17; 22; 36; 48; 52; 127; 212$
- $k = 300$
- Die Anzahl der Vergleiche beträgt $26$: jeweils zwei Mal mit jedem Element der Folge.
Laufzeit im worst case
In dieser Vorlesung wird sich für die längste Laufzeit interessiert, die man für alle zulässigen Eingaben erhalten kann (worst case Analyse). Bei der linearen Suche gilt offenbar: Die Suche nach einem Element $k$ in einer sortieren Folge mit $n$ Elementen benötigt nie mehr als $2n$ Vergleiche (von $k$ mit Elementen aus der gegebenen Folge). Es kann also die Anzahl $V$ dieser Vergleiche im worst case als Funktion dargestellt werden:
- $V$: $\mathbb{N}\rightarrow \mathbb{N} $ mit $V(n)= 2n$
Analog kann dieser Algorithmus als eine Funktion:
- $T$: $\mathbb{N}\rightarrow \mathbb{N}$
betrachtet werden, wobei $T(n)$ die maximale Anzahl von elementaren Anweisungen ist (nicht nur von Vergleichen!), die für eine Eingabefolge mit $n$ Elementen ausgeführt werden.
Laufzeit im worst case mittels Array
- Man erhält: $T(n) = 5n + 3$
Laufzeit im worst case mittels Linked List
- Man erhält: $T(n)=6n+4$
Vergleich der Laufzeit der Linearen Suche mittels Array und mittels Linked List
| n | Lineare Suche mittels Array: $T(n)=5n+3$ | Lineare Suche mittels Linked List: $T(n)=6n+4$ |
|---|---|---|
| 4 | 23 | 28 |
| 16 | 83 | 100 |
| 256 | 1283 | 1540 |
| 4096 | 20483 | 24500 |
| 65536 | 327683 | 393220 |
| 1048576 | 5242883 | 6291460 |
| 16777216 | 83886083 | 100663300 |
Idee zur Beschleunigung der Suche
Wenn die sortierte Folge als Array gegeben ist, dann kann $k$ im ersten Schritt mit einem beliebigen Element in der sortierten Folge verglichen werden. Man muss also nicht von vorn nach hinten durchlaufen wie in einer verketteten Liste.
Beispiel 1:
- $k = 37$
- Folge: $5; 7; 9; 10; 14; 16; 17; 22; 36; 48; 52; 127; 212$
- Man kann $k$ mit dem Element an Position $3$ vergleichen (also mit der $10$).
Ergebnis: Wenn die $37$ überhaupt in der sortierten Folge enthalten ist, dann muss sie an einer Position größer oder gleich $4$ stehen.
Beispiel 2:
- $k = 37$
- Folge: $5; 7; 9; 10; 14; 16; 17; 22; 36; 48; 52; 127; 212$
- Ebenso könnten wir $k$ mit dem Element an Position $9$ vergleichen (also mit der $48$).
Ergebnis: Wenn die $37$ überhaupt in der sortierten Folge enthalten ist, dann muss sie an einer Position kleiner oder gleich $8$ stehen.
Beachte: In beiden Fällen führt ein Vergleich zum Ausschluss einer ganzen Reihe von Elementen der sortierten Folge für die weitere Suche.
Man möchte nun gerne eine Garantie folgender Art: Nach dem Vergleich von $k$ mit einem geeigneten Element der sortierten Folge können immer mindestens $x$ Elemente von der weiteren Suche ausgeschlossen werden.
Algorithmus binäre Suche
Gegeben ist eine sortierte Folge in einem Array $A$ der Länge $n$ und das gesuchte Element $k$.
Die Arbeitsweise ist folgende:
- 1. Mit $u$ und $o$ seien im Folgenden immer die erste und die letzte Position im Array bezeichnet, zwischen denen $k$ liegen muss (wenn es überhaupt in $A$ enthalten ist).
- 2. Setze $u = 0$ und $o = n -1$.
- 3. Solange $u \leq o $
- 3.1 Berechne $p=[(o+u)/2]$.
- 3.2 Falls $A[p]=k$ ist, brich die Suche ab und gib die Position $p$ aus.
- 3.3 Sonst
- 3.3.1 Falls $A[p]<k$ ist, setze $u =p+1$.
- 3.3.2 Sonst setze $o = p -1$.
- 4. Gib nicht enthalten aus.
Umsetzung in Java
Laufzeit der binären Suche im worst case
Anzahl der Durchläufe im worst case
Für $T(n)$ gilt: $T(n) = 5 + 8$ * Anzahl der Durchläufe der while-Schleife
Sei $n$ die Länge des zu durchsuchenden Arrays.
- Nach dem ersten Durchlauf sind höchstens
$\lfloor n/2 \rfloor \leq n/2$
Elemente übrig, die noch durchsucht werden müssen.
- Nach dem zweiten Durchlauf sind höchstens
$\lfloor\lfloor n/2 \rfloor/2 \rfloor \leq n/(2^2)$
Elemente übrig, die noch durchsucht werden müssen.
- Nach dem dritten Durchlauf sind höchstens
$\lfloor\lfloor\lfloor n/2 \rfloor /2 \rfloor /2\rfloor \leq n/(2^3)$
Elemente übrig, die noch durchsucht werden müssen.
Allgemein:
- Nach $i$ Durchläufen sind höchstens
$n/(2^i)$
Elemente übrig, die noch durchsucht werden müssen.
- Wir müssen also das kleinste $i$ finden, für welches
$n/(2^i)<1$
gilt.
- Es gilt: $n/(2^i)<1 \Leftrightarrow n<2^i \Leftrightarrow log_2 n<i$
Ergebnis:
Für ein Array der Länge $n$ kann es also höchstens $1+log_2 n$ Durchläufe der while-Schleife geben.
Damit ergibt sich für Laufzeit im worst case:
$T(n) \leq 8log_2 n + 13$.
Vergleich der Laufzeit von Linearer Suche und Binärer Suche
| n | lineare Suche: $T(n)=5n+3$ | binäre Suche: $T(n)\leq 8log_2 n +13$ |
|---|---|---|
| 4 | 23 | 29 |
| 16 | 83 | 45 |
| 256 | 1283 | 77 |
| 4096 | 20483 | 109 |
| 65536 | 327683 | 141 |
| 1048576 | 5242883 | 163 |
| 16777216 | 83886083 | 205 |
In den meisten Fällen ist man bei der Analyse der Laufzeit nur am asymptotischen Verhalten der Funktion $T(n)$ interessiert, welche in der $O$-Notation festgehalten ist:
- Die worst case Laufzeit der linearen Suche in einer sortierten Folge von $n$ Elementen ist $O(n)$.
- Die worst case Laufzeit der binären Suche in einer sortierten Folge von $n$ Elementen ist $O(log_2 n)$.
Bei dieser Analyse sollte noch zusätzlich erwähnt werden, dass die Laufzeit abhängig von der Laufzeit des eventuell voran gegangenen Sortieralgorithmus ist. Um die Suche in Daten zu optimieren sollte man den zusätzlichen Aufwand, einen Sortieralgorithmus davor zu programmieren, in Kauf nehmen, da die Effizienz dadurch erheblich gesteigert werden kann.
| Name | Best Case | Average Case | Worst Case |
|---|---|---|---|
| Selection Sort | $\mathcal{O}(n^2)$ | $\mathcal{O}(n^2)$ | $\mathcal{O}(n^2)$ |
| Insertion Sort | $\mathcal{O}(n)$ | $\mathcal{O}(n^2)$ | $\mathcal{O}(n^2)$ |
| Mergesort | $\mathcal{O}(n \cdot log(n))$ | $\mathcal{O}(n \cdot log(n))$ | $\mathcal{O}(n \cdot log(n))$ |
| Quicksort | $\mathcal{O}(n \cdot log(n))$ | $\mathcal{O}(n \cdot log(n))$ | $\mathcal{O}(n^2)$ |
| Countingsort | $\mathcal{O}(n+m)$ | $\mathcal{O}(n+m)$ | $\mathcal{O}(n+m)$ |
| Heapsort | $\mathcal{O}(n \cdot log(n))$ | $\mathcal{O}(n \cdot log(n))$ | $\mathcal{O}(n \cdot log(n))$ |
Einfügevorgang in einer sortierten Liste
Der interne Aufbau einer sortierten Liste unterscheidet sich nur unwesentlich von einer unsortierten Liste. Wichtig ist, dass sie nicht nachträglich sortiert (wie z.B. bei Arrays üblich), sondern von Anfang an sortiert aufgebaut wird. Das heisst: Bereits beim Einfügen eines neuen Elements erhält dieses seine richtige Position in der Sortierreihenfolge - ein neuer Knoten wird nicht einfach an das Listenende angehängt, sondern an der passenden Position in die Liste eingefügt.
- Die Liste wird elementweise durchlaufen und dabei wird durch eine Vergleichsoperation mit den bereits vorhandenen Elementdaten die richtige Einfügeposition für den neuen Knoten bestimmt. Hierbei ist der Sortieralgorithmus zu beachten (aufsteigend oder absteigend etc.).
- Wenn die richtige Position gefunden ist, wird ein neuer Knoten erzeugt. Der Zeiger des vorausgegangenen Knotens wird auf den neu eingefügten Knoten gesetzt und der Zeiger des eingefügten Knotens auf den nachfolgenden Knoten. Entsprechend wird bei einer beidseitig verketteten Liste auch der Rückzeiger versetzt.
Das Entfernen eines Datenelements verläuft analog: Auffinden des gesuchten Elements, dann Zeiger versetzen und Element löschen. Auch hierbei muss insbesondere das Versetzen der Zeiger sorgfältig programmiert werden, um das Zerbrechen der Liste und damit Datenverlust zu vermeiden.
Vorgehensweise
Eine sortierte Liste kann mit unterschiedlichen Algorithmen zum Auffinden der passenden Einfüge- bzw. Löschposition implementiert werden.
- Beim Durchlaufen der Liste wird nur ein einziger Suchzeiger benutzt. Zum Einfügen oder Löschen eines Elements muss dann jedoch ein temporärer Hilfszeiger verwendet werden, der die Adresse des folgenden Elements zwischenspeichert, bis die Operation abgeschlossen ist.
- Auf den temporären Hilfszeiger kann verzichtet werden, wenn zwei Suchzeiger zum Durchlaufen der Liste benutzt werden. Sie laufen im Schrittabstand parallel und zeigen auf die benachbarten Elemente.
Temporärer Hilfszeiger
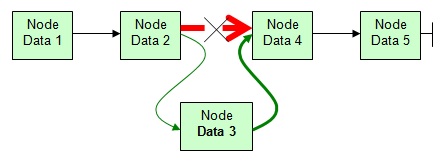
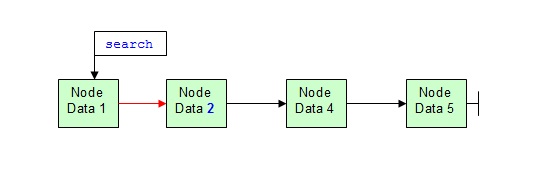
Im folgenden Beispiel soll der Datensatz "3" in eine sortierte Liste eingefügt werden. Der Suchzeiger steht zu Beginn am Listenkopf.
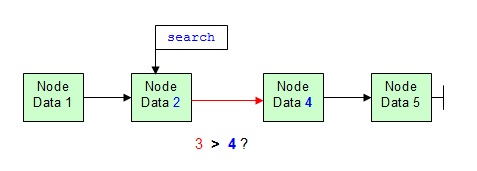
Zum Auffinden der richtigen Einfügeposition rückt der Suchzeiger elementweise weiter. Dabei wird über den next-Zeiger das jeweils folgende Element geprüft, ob es grösser oder kleiner ist als das einzufügende Element.
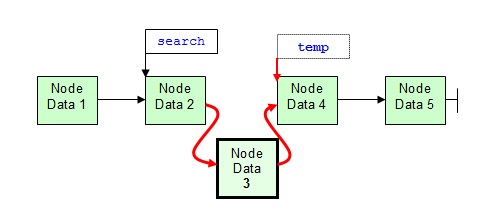
Wenn die Bedingung zutrifft, dann ist die richtige Einfüge-Position für das neue Element ("3") gefunden. Nachdem das neue Element erzeugt wurde, kann der next-Zeiger des aktuellen Elements umgesetzt werden. Dies darf allerdings erst geschehen, nachdem ein temporärer Hilfszeiger (temp) die Adresse des nachfolgenden Elements gesichert hat. Dann kann der next-Zeiger des vorhergehenden Elements auf die Adresse des neuen Elements gesetzt werden und der next-Zeiger des neuen Elements auf die Adresse des nachfolgenden Element, die im temporären Hilfszeiger aufbewahrt worden ist. Der Hilfszeiger wird danach nicht mehr gebraucht.
Zwei nicht-temporäre Zeiger
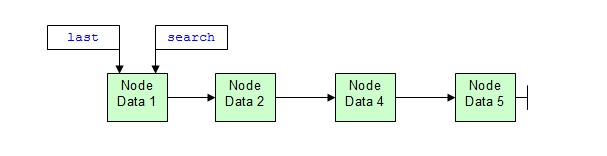
Beim Durchlaufen der Liste können alternativ auch zwei Zeiger eingesetzt werden. Am Beginn des Suchlaufs zeigen beide Zeiger zunächst gemeinsam auf den Listenkopf.
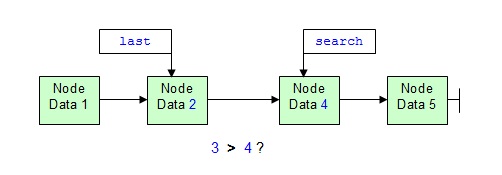
Beim folgenden Suchvorgang zeigt der last-Zeiger auf den jeweils vorhergehenden Knoten (weil dessen next-Zeiger auf den neuen Knoten umgesetzt werden muss) und der Suchzeiger auf den aktuellen Knoten. So durchläuft der search-Zeiger die Liste knotenweise bis zum Ende und vergleicht dabei die Daten jedes Knotens mit den Daten des einzufügenden Knotens. Der last-Zeiger bleibt also immer eine Position zurück.
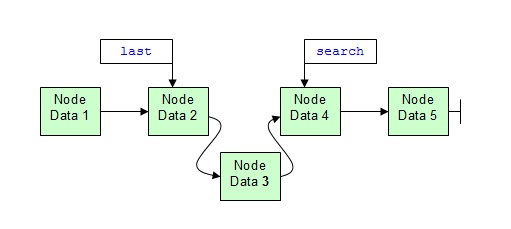
Wenn die passende Position für den neuen Knoten in der sortierten Liste gefunden ist, dann wird der next-Zeiger des last-Knotens auf den neuen Knoten gesetzt und der next-Zeiger des eingefügten Knotens auf den search-Knoten. Damit ist der neue Knoten in der sortierten Liste an der richtigen Position verankert.
Beispiele für sortierte Listen
- Binäre Suchbäume
- AVL-Bäume
- Rot-Schwarzbäume
- Randomisierte Suchbäume
- skip-Listen
- Sparse Table
Übungen
1. Setzen Sie einen der vorgestellten Suchalgorithmen in der Programmiersprache Ihrer Wahl um und testen Sie ihn mit verschiedenen Datentypen. Führen Sie für jeden Datentyp mehrere Durchläufe durch und messen Sie die Zeit. Nutzen Sie als Zeitangabe Nanosekunden, um möglichst exakte Ergebnisse zu erhalten.
2. Was schließen Sie aus den gewonnenen Ergebnissen?
Lösungen
1.
2.
Weblinks
[1] Galileo Computing
[2] Wikipedia