Sortierte Folgen SS12
Aus ProgrammingWiki

Inhaltsverzeichnis |
Bäume
Ein Baum ist eine zweidimensionale verkettete Datenstrucktur. Ein Baum definiert sich dadurch, dass er entweder leer ist oder er enhält ein Element und weitere Teilbäume. Ein Baum ist leer, wenn er nur aus einem äußeren und keinem inneren Knoten besteht. Somit ist ein Baum eine nicht leere Menge aus Knoten und Kanten. Der Nutzten eines Baumes beschäftigt sich mit der Strukturierung der inneren Knoten, die äußeren Knoten dienen lediglich als Platzhalter. Muss ein Knoten eine konkrete Anzahl n an direkten Nachfolgern aufweisen so spricht man von einem n-ären Baum. In solchen Bäumen ist es zwäckmäßig sinnfoll spezielle äußere Knoten festzulegen, die weder nachfolger noch spezielle Informationen enthalten. Solch spezielle Knoten lassen sich duch null bzw. NIL festlegen. Zu beachten ist dass jeder Binäre Baum ein Baum ist jedoch nicht jeder Baum ein binärer Baum.
Terminologie
- Knoten - Datenstruktur zur Speicherrung eines Tupels
- Baum - Menge von Knoten und Kanten
- Wald - Menge von Bäumen
- Kante - Verbindung zwischen zwei Knoten
- Pfad - Folge verschiedener, durch Kanten verbundener, Knoten
- Wurzel - Startknoten ohne Vorgänger
- Blatt - Knoten ohne Nachfolger( auch äußere oder Nichtendknoten )
- innere Knoten - Knoten mit mindestens einem Nachfolger
- Vater - Vorgänger eines Knotens
- Bruder - Knoten mit dem Selben Vaterknoten
- Sibling - Bruder eines Knotens
- Großvater - Vorgänger des Vaterknotens
- Onkel - Bruder des Vaters
- Aufgabe: Entwerfen Sie den Syntaxbaum für die Operation ( 3 + 5 ) * ( 4 * ( 5 + 3 ) ). Geben Sie die Höhe des entstandenen Baumes an.
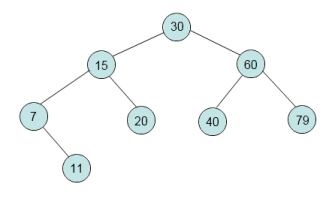
Binäre Suchbäume
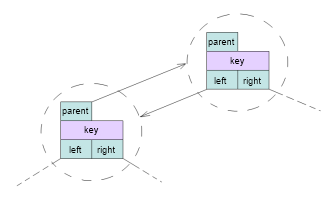
Eine spezialisierung eines binären Baumes ist der binäre Suchbaum. Der binäre Suchbaum besitzt die Eigenschaft, dass der Schlüssel des linken Kindknotens vom Knoten N jeweils kleiner oder gleich dem Schlüssel von N ist, wobei der Schlüssel des rechten Kindknotens größer ist als der von N. Daraus folgt, dass wenn Y ein Schlüssel im linken Teilbaum von N, und X ein Schlüssel im rechten Teilbaum von N ist, dann ist der Schlüssel von Y kleiner oder gleich dem Schlüssel von N und N ist kleiner X. Ein binärer Suchbaum repräsentiert sich durch seine verkettete Datenstruktur, in welcher jeder Knoten ein Objekt darstellt. Jeder Knoten enthält dabei folgende Attribute:
- einen Zeiger auf den Elternknoten
- einen Zeiger auf den linken Kindknoten
- einen Zeiger auf den rechten Kindknoten
- einen Schlüssel
Besitzt der jeweilige Knoten keine Kinder oder kein Elternelement, zeigt das entsprechende Attribut auf null bzw. auf NIL, wobei NIL ein auch ein Knoten repräsentiert dessen Zweck, ebenso wie bei null, darin besteht, den binären Suchbaum terminieren zu lassen.
Die Grundoperationen in einem binären Suchbaum sind:
- insert( Tupel ) - zum Einfügen eines neuen Datensatztes
- delete( Node ) - zum Löschen eines Knotens
- search( Key ) - Zum suchen eines Schlüssels im Baum
- getMin( ) - zum Erhalt des minimalen Knotens
- getMax( ) - zum Erhalt des maximalen Knotens
- getSuccessor( Node ) - zum Erhalt des nachfolger eines Knotens
- getPredecessor( Node ) - zum Erhalt des Vorgängers eines Knotens
- InorderTraversation( ) - zur Ausgabe des Baumes nach der Inorder-Traversierung
- PreorderTraversation( ) - zur Ausgabe des Baumes nach der Preorder-Traversierung
- PostorderTraversation( ) - zur Ausgabe des Baumes nach der PostorderTraversierung
Einfügen eines Elementes
Beim Einfügen eines Elementes macht man sich die Eigenschaft zunutze, dass der Schlüssel des linken Sohns jeweils kleiner oder gleich dem Schlussel ist, den der Knoten selbst enthält. Der rechte Kindknoten dagegen enthält einen echt größeren Schlüssel. Fügt man also einen Schlüssel in den Baum ein so beginnt man beim Vergleich mit der Wurzel. Ist der Einzufügende Schlüssel größer als der Schlüssel der Wurzel, so setzt man den Vergleich im rechten Teilbaum des aktuellen Knotens fort. Andernfalls also wenn der Schlüssel kleiner oder gleich dem Schlüssel der Wurzel ist, setzt man den Vergleich im linken Teilbaum des aktuellen Knotens fort. Trifft man bei diesem Verfahren auf einen Knoten dessen Wertigkeit null entspricht, so wird an dieser Stelle der neue Schlüssel eingefügt. Für den Programmablauf lässt sich also folgendes allgemein formulieren:
- Abfrage ob der einzufügende Schlüssel größer oder gleich dem Schlüssel von N ist
- Abfrage ob der sich daraus ergebende Kindknoten dem Wert null entspricht
- wenn ja, dann erzeuge neuen Knoten mit dem einzufügenden Schlüssel
- sonst beginne mit Schritt 1 wobei N nun N.links bzw n.rechts ist
Für die Methode zum Einfügen in einen BST ergibt sich zum einen eine rekursive sowie eine iterative Umsetzungsmöglichkeit, die im folgenden durch Pseudocode beschrieben werden.
- Rekursive Implementierung:
InsertRek( Schlüssel K, Knoten N )
if Schlüssel < N.Schlüssel do
if N.links is null do
N.links = neuer Knoten
N.links.Schlüssel = K
N.links.Vater = N
else do
InsertRek( K, N.links )
else
if N.rechts is null
N.rechts = neuer Knoten
N.rechts.Schlüssel = K
N.rechts.Vater = N
else do
InsertRek( K, N.rechts )
- Iterative Implementierung:
InsertIt( Schlüssel K )
Knoten p = Wurzel
Knoten o = null
while p not null
o = p
if K < p.schlüssel or K is p.schlüssel
p = p.links
else if K > p.schlüssel
p = p.rechts
else return
p = neuer Knoten
p.Schlüssel = K
p.Vater = o
if Wurzel is null
Wurzel = p
else if K < o.schlüssel or K is o.schlüssel
o.links = p
else o.rechts = p
Finden eines Elementes
Beim suchen eines Elementes wird die spezielle Anordnung der Elemente in einem Baum genutzt. Ist der Baum leer, so ist der Schlüssel nicht enthalten. Ist das zu suchende Element größer als der Schlüssel der Wurzel bzw. des Knotens des aktuellen Teilbaumes so vergleicht man dessen rechten Kindknoten, ist er gleich so wurde das gesuchte Element gefunden ansonsten vergleicht man die Wurzel bzw. den linken Kindknoten des aktuellen Knotens. Beinhaltet der binäre Suchbaum ein oder mehrere Duplikate, so wird immer nur der Schlüssel gefunden, der den gerringsten Weg zu Wurzel des Baumes besitzt, also der Schlüssel mit der geringsten Tiefe. Folgende Schritte sind also beim Einfügen durchzuführen:
- Abfrage ob der Baum leer ist
- Vergleich ob der gesuchte Schlüssel der Schlüssel des Wurzelelementes ist
- Wenn Schlüssel kleiner oder gleich ist, dann suche im linken Teilbaum weiter sonst rechts
- Rekursive Implementierung:
searchRek( Schlüssel k, Knoten n )
if n is null
return null
if k is n.schlüssel
return n
if k < n.schlüssel
return searchRek( k, n.links )
else return searchRek( k, n.rechts )
- Iterative Implementierung:
searchIt( Schlüssel k, Knoten n )
Knoten nI = n
while nI not null and nI.schlüssel not k
if k < nI.schlüssel
nI = nI.links
else nI = nI.rechts
return nI
Finden des Minimums
Um den minimalen Schlüssel im Baum zu finden wandert man einfach von der Wurzel beginnend immer am linken Teilbaum entlang, bis der nächst folgende Knoten den Wert null enthält. Enthält der linke Teilbaum den Wert null, so terminiert der Algorithmus und gibt eine Adresse auf das gesuchte Minimum zurück.
- Iterative Implementierung:
Knoten getMinIt( Knoten wurzel )
if wurzel is null
return null
while wurzel.links not null
wurzel = wurzel.links
return wurzel
- Rekursive Implementierung:
Knoten getMinRek( Knoten wurzel )
if wurzel is null
return null
else if wurzel.links is null
return wurzel
else return getMinRek( wurzel.links )
Finden des Maximums
Um den maximalen Schlüssel im Baum zu finden wandert man einfach von der Wurzel beginnend immer am rechten Teilbaum entlang, bis der nächst folgende Knoten den Wert null enthält.
- Iterative Implementierung:
Knoten getMaxIt( Knoten wurzel )
if wurzel is null
return null
while wurzel.rechts not null
wurzel = wurzel.rechts
return wurzel
- Rekursive Implementierung:
Knoten getMaxRek( Knoten wurzel )
if wurzel is null
return null
else if wurzel.rechts is null
return wurzel
else return getMaxRek( wurzel.rechts )
Finden des Nachfolgers
Der Nachfolger eines Knotens ist der Knoten, dessen Schlüssel gemäß der Ordnugsrelation größer ist. Existieren Duplikate, so ist der Nachfolger der Vaterknoten. Das Sohnelement muss in diesem Fall notwendigerweise ein linker Sohn sein. Der Nachfolger eines Knotens ist daher entweder das Minimum des rechten Teilbaumes oder, falls dieser nicht vorhanden, der Vaterknoten.
- Implementierung:
NachfolgerIt( Knoten n )
if n is null
return null
if n.rechts not null
return getMin( n.rechts )
Knoten oben = n.vater
while oben not null and oben.rechts is n
n = oben
oben = n.o
return oben
Traversierung eines binären Suchbaumes
Die Eigenschaften eins binären Suchbaumes erlauben es uns den Baum komplett rekursiv zu durchlaufen. Hierbei unterscheidet man in drei versiedene Traversierungsmöglichkeiten. Zum einen ist dies die Inorder-Traversierung, wobei der Schlüssel des Teilbaumes zwischen den Werten seines linken und rechten Teilbaumes ausgegeben wird. In diesem Falle liegt die Ausgabe je nach implementierung auf- bzw. absteigend vor. Die zwei anderen Möglichkeiten den Baum zu traversieren, sind die Preorder- und die Postorder-Traversierung. Bei der Preorder-Traversierung wird der Schlüssel vor den Schlüsseln seines linken und rechten Teilbaums ausgeben und bei der Postorder-Traversierung hinter ihnen.
- Inorder-Traversierung:
inorderTreewalk( Node n )
if n not null
inorderTreewalk( n.left )
print( n.key )
inorderTreewalk( n.right )
- Preorder-Traversierung:
preorderTreewalk( Node n )
if n not null
print( n.key )
preorderTreewalk( n.left )
preorderTreewalk( n.right )
- Postorder-Traversierung:
postorderTreewalk( Node n )
if n not null
postorderTreewalk( n.left )
postorderTreewalk( n.right )
print( n.key )
- Aufgabe: Geben Sie eine weiter Methode zur sortierten Ausgabe des Baumes an, die analog zur inorder.Traversierung genutzt werden kann. Nutzen Sie dazu die bisher kennengelernten Mehotden.
Löschen eines Elementes
Das löschen eines Knotens in einem BST stellt sich als komplexer heraus. So muss eine grundsätzliche Entscheidung vorgenommen werden, ob der zu löschende Knoten höchstens ein oder zwei Kinder hat.
Mit einem Sohn
Wenn der zu löschende Knoten keine Kinder hat kann er bedenkenlos gelöscht werden, hat er allerdings genau ein Kind, so wird der verbleibende Teilbaum einfach eine Etage nach oben geschoben. Man setzt also den Vorgängerknoten des Kindknotens auf den Entsprechenden linken oder rechten Kindknoten des Vorgängerknotens des zu löschenden Elementes sowie den entsprechend linken oder rechten Kindknoten dieses Elementes auf das Kindelement des zu löschenden Knotens. Ist der zu löschende Knoten die Wurzel, so setzen wir den Wurzelzeiger einfach auf den entsprechend folgenden Knoten.
- Implementierung:
deleteNodeWithOneChild( Node n )
// get the child
Node child;
if n.left is null
child = n.right
else child = n.left
// handling if the root should be deleted
if n is root
child.parent = null
root = child
return
// handling if the node has a parent node
if n.parent.left is n
n.paretn.left = child
else n.parent.right = child
if child not null
child.parent = n.parent
n = null
Mit zwei Söhnen
Beinhaltet der zu löschende Knoten zwei nichtleere Kindknoten, so wird zunächst der kleinste Knoten des rechten Teilbaums ermittelt. Dieser ist da er im rechten Teilbaum ist in jedem Falle der Nachfolger von dem zu löschenden Knoten und beinhaltet keinen linken Kindknoten mehr. Somit wird einfach der Inhalt dieses Knotens in den zu löschenden Knoten kopiert und anschließend das ermittelte minimum gelöscht. Man vereinfacht mit dieser Methode also den Fall, dass zwei Söhne existieren, zu dem Fall, dass nur ein Sohn existiert womit die löschfunktion für einen Kindknoten angewand werden kann. Beinhaltet der BST allerdings Duplikate, so würde die oben beschiebene Vorgehensweise zu Komplikationen führen. Würde man also nur das Minimum, welches ein Duplikat im Baum aufweist( dieses Duplikat wäre dann zwangsweise das Elternelement des Minimums ), an den Platz des zu löschenden Knotens kopieren, so würden hierbei Duplikate im rechten Teilbaum des zu gelöschten Elementes übrig bleiben. Diese Fehlplatzierung würde demnach die Invariante binärer Suchbäume verletzen. Um dieses Problem zu beseitigen wird an die Position des zu löschenden Knotens die Liste aller Duplikate des Minimums aus dem rechten Teilbaum eingefügt. Somit wird der Elternknoten-Zeiger der Entsprechenden Kindknoten des zu löschenden Elementes auf das Minimum im linken Teilbaum gesetzt und dessen Kindzeiger auf die Kinder des zu löschenden Knotens. Im folgenden wird dann der Kindzeiger des zu löschenden Knotens auf das Kindelement des Duplikates mit der geringsten Tiefe gesetzt und dessen Elternpointer auf das zu löschende Element. Anschließend wird der Inhalt des im rechten Teilbaum übriggebliebenen Duplikates in das zu löschende Element kopiert. Da das im rechten Teilbaum übriggebliebende Element nun im schlimmsten Fall noch einen rechten Sohn beinhaltet, kann dieses Element nun mit der oben beschriebenen Methode zum Löschen eines Elementes entfernt werden.
- Implementierung:
deleteNodeWithTwoChildren( Node n )
Node min = getMin( n.right )
min.left = n.left
if min.left not null
min.left.paretn = min
// walking up if there are duplicates
while min.key is min.parent.key
min = min.parent
n.left = min.left
if n.left is null
n.left.parent = n;
min.left = null
n.key = min.key
deleteNodeWithOneChild( min )
Komplexität
Beim binären Suchbaum laufen die Operationen für das Einfügen, Löschen, Suchen, Minimum und das Maximum je in $O( lg( h ) )$ ab, wobei $h$ die Höhe des Baumes darstellt. Für einen Ausbalancierten Baum beträgt die Höhe näherungsweise $lg( n )$ wobei $n$ die Anzahl der Elemente ist. Werden die Elemente jedoch beispielsweise in sortierter Reihenfolge in den Suchbaum eingefügt, so entartet der binäre Suchbaum zu einer ansatzweise doppelt verketteten Liste( ansatzweise, da das letzte Element nicht auf die Wurzel zeigt und die Wurzel nicht auf das letzte Element), woduch der Aufwand für die aufgeführten Operationen somit $O( n )$ beträgt und damit linear verläuft. Die In- Post- und Preorder-Traversierung besitzt einen Aufwand von $O( n )$, da sie durch ihren mehrfach rekursiven Charakter jeden Knoten exakt einmal besucht.
Programmierbeispiel
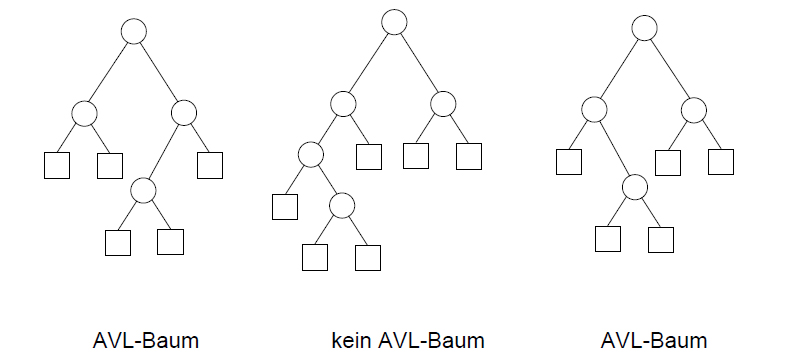
A-V-L-Bäume
Eigenschaften
- balancierte Knoten
- Höhenunterschied = 1
- Rotation um Angelknoten
- ausbalancierter binärer Baum
Balancekriterium
Höhenunterschied = HöheRechts - HöheLinks
Suchen
Bei der Suche ist es entscheidend zu wissen, dass ein AVl-Baum ein spezieller Binärer Baum ist, wodurch man sich dessen Vorgehensweise zunutze machen kann. Wie in jedem Baum beginnt die Suche in der Wurzel, wobei die ersten zwei Möglichkeiten auftreten. Zum einen kann das gesuchte Elemente der Schlüssel der Wurzel sein, wodurch die Suche an der Stelle beendet ist. Andern Falls muss die Entscheidung gefällt werden ob das Element kleiner oder größer als das aktive Element ist. Nach diesem Kriterium geht man rekursiv der entsprechenden Verkettung entlang bis das aktuelle Element dem gesuchten entspricht. Dabei ist zu beachten, dass wenn das gesuchte Element kleiner oder größer als das aktive Element ist, aber keine Verkettung zu dem entsprechenden kleineren oder größeren Kindsknoten führt, das Element nicht im Baum vorhanden ist. Durch das ausbalancieren des Baumes während des Einfügens oder Löschens wird das Suchen optimiert, da der Baum nicht unnötig in die breite wächst, was unnötige Verzweigungen mit sich bringen würde.
Einfügen
Beim Einfügen wird zunächst die Position i, an der der Schlüssel eingefügt werden soll, ermittelt. Dabei kann die Position links, mittig oder rechts im Teil-Baum liegen. Das Einfügen an sich erfolgt als Anhängen eines neuen Blattes an der ermittelten Position i. Nun gilt es an dieser Position herauszufinden ob das eingefügt Element kleiner bzw. größer als der Vaterknoten ist um es somit als linke oder rechte Verkettung anzuhängen. Dabei kann es vorkommen, dass durch Besetzung von kleineren Blättern, es nötig ist das eingefügte Blatt mit dem aktuellen Vaterknoten(vorher Blatt) zu tauschen. Des weiteren muss die Balance, was das wichtigste Kriterium gegenüber dem Binären-Baum ist, beachtet werden. Das bedeutet, dass lediglich ein Höhenunterschied von 1 legal ist. Durch das Einfügen eines Elements jedoch kann es vorkommen, dass der Unterschied 2 betragen kann. Diese Verletzung des Kriteriums wird durch Rotation behoben.
worst case: $O$(log n)
Löschen
Das Ermitteln des zu löschenden Elements kann durch eine Suche erfolgen. Wie bei dem Binär-Baum gibt es auch hier verschiedene Fälle zu beachten. Zum einen kann das zu löschende Element ein Knoten sein, wo nach dem Löschen die Blätter/Kindsknoten neu angehangen werden müssen. Dabei wird das Vorgänger-Element zum neuen Vaterknoten. Zum anderen kann der Fall auftreten, dass das Element ein Blatt ist was hingegen der leichtere Fall ist, da hierbei nur der Schlüssel gelöscht wird. Auch nach einem Löschvorgang müssen die Balancewerte des Baumes wieder überprüft werden um herauszufinden ob eine Rebalancierung nötig ist. Diese tritt in Kraft sobald der Höhenunterschied zwischen den Ebenen 2 ergibt. Bei der Rebalancierung gibt es zwei verschiedene Arten. Die Doppelrotation, wobei der Baum nach der Rotation die Höhe des Baums um 1 verringert wird und die Einfachrotation bei der die Baumhöhe gleich der Höhe ist, wie vor dem Löschvorgang.
worst case: $O$(log n)
Einfachrotation
Bei der Rebalancierung durch Rotation wird die Baumstruktur lokal geändert. Somit liegt bei der Rotation die Konzentration auf Teil-Bäumen, bei denen min ein Bruder 2 Ebenen höher ist als der Angelknoten. Je nachdem ob der Angelknoten dabei links oder rechts vom aktuellen Teil-Baum liegt, wird eine Links- oder Rechtsrotation durchgeführt, die die Blätter des Teilbaumes um eine Ebene verringern und somit die Balance wiederherstellen.
Doppelrotation
Eine Doppelrotation ist nichts anderes als eine hintereinander ablaufende Links-Einfachrotation und eine Rechts-Einfachrotation, die anstatt nur einen Höhenunterschied zwei Höhenunterschiede von 2 behebt.
Applet-Link
http://alfi.ira.uka.de/lehre/sommer2002/AVLTreeApplet/avl.html
Rot-Schwarz-Bäume
Eine weitere Möglichkeit binäre Bäume zu balancieren besteht in der Verwendung der Rot-Schwarz-Bäume. Rot-Schwarz-Bäume stellen eine Spezialisierung der binären Suchbäume dar und ermöglichen durch ihre besonderen Eigenschaften, die im Folgenden näher beschrieben werden, einen näherungsweise balancierten Baum zu konstruieren.
Komponenten der Knoten
- Farbe
- Schlüssel
- Adresse des Eleternknotens
- Adresse des linken Kindknotens
- Adresse des rechten Kindknotens
Eigenschaften
- Jeder Konten ist entweder rot oder schwarz
- Die Wurzel ist schwarz
- Jedes Blatt( null/ nil ) ist schwarz
- Die Kind-Knoten eines Roten Knotens sind jeweils schwarz
- Alle Pfade die von einem bestimmten Knoten ausgehen und in einem Blatt dieses Teilbaums enden, haben die gleiche Anzahl an schwarzen Knoten
Rotationen
Durch die Einfüge- und Löschoperationen kann es dazu kommen, das eine oder mehrere Eigenschaften des Rot-Schwarzbaumes verletzt werden. Um die Zeigerstruktur des Baumes zu "reparieren" bedient man sich der Rotation. Hinzukommend verringert sich durch eine Rotation die Höhe des Baumes um eins.
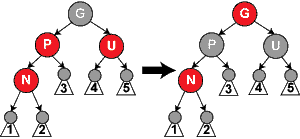
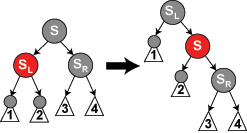
Linksrotation
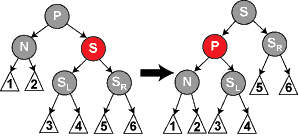
Vorraussetzung für die Linksrotation um einen Knoten N ist, dass das rechte Kind K von N nicht null bzw. NIL ist. Bei der Linksrotation wird das Verhältnis zwischen N und seinem Kind "umgedreht". So ist nach der Linksrotation K die neue Wurzel des Teilbaumes und N das linke Kind von K. Das ehemalige linke Kind von K ist nun das rechte Kind von N.
rotateLeft( Node n )
if n not null
if n.right not null
Node parent = n.parent
Node child = n.right
if n is parent.right
parent.right = child
child.parent = parent
n.parent = child
n.right = child.left
n.right.parent = n;
child.left = null
if n is parent.left
parent.left = child
child.parent = parent
n.parent = child
n.right = child.left
n.right.parent = n;
child.left = null
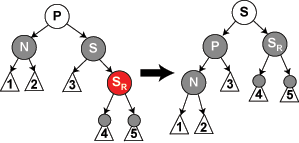
Rechtsrotation
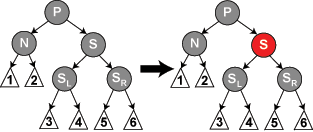
Die Rechtsroatation stellt das Äquivalent zur Linksrotation dar. So ist die Vorraussetzung für die Rechtsrotation um einen Knoten N, dass sein linkes Kind K nicht null bzw. NIL ist. Die Rechtsroation bewirkt nun, dass die K zur neuen Wurzel des Teilbaums aufsteigt und N zum rechten Kind von K absteigt. Das ehemalige rechte Kind von K ist nun das linke Kind von N.
rotateLeft( Node n )
if n not null
if n.right not null
Node parent = n.parent
Node child = n.right
if n is parent.right
parent.right = child
child.parent = parent
n.parent = child
n.left = child.right
n.left.parent = n;
child.right = null
if n is parent.left
parent.left = child
child.parent = parent
n.parent = child
n.left = child.right
n.left.parent = n;
child.right = null
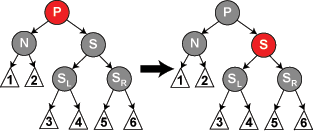
Einfügen
Das Einfügen in einen Rot-Schwarz-Baum geht prinzipiell wie bei einem binären Suchbaum von statten. Hinzu kommt allerdings, dass die neu eingeführten Knoten jeweils immer rot sind. Da duch die rote Farbe jedes neuen Knotens nicht gewähleistet ist, dass alle Eigenschaften des Rot-Schwarz-Baumes erfüllt sind, werden die im folgenden fünf Fälle berücksichtigt und angewand. Für eine einfachere Lesbarkeit und ein besseres Verständnis werden im Folgendem ebenso Methoden zur Rückgabe des Großvaters und des Onkels aufgeführt.
grandparent( Node n ) return n.parent.parent
uncle( Node n )
if n.paretn is grandparent( n ).left
return grandparent( n ).right
else return grandparent( n ).left
- Fall 1:
Der erste Fall beschreibt den Sachverhalt, dass der neu eingefügte Knoten die Wurzel des Baumes darstellt. Dies würde berreits die Eigenschaft, dass die Wurzel des Baumes schwarz sein muss verletzen. Aus diesem Grund wird die noch rote Wurzel schwarz gefärbt wodurch das Gleichgewicht wieder hergestellt ist.
insertCase1( Knoten n )
if n.parent is null
n.color = BLACK
else insertCase2( n )
- Fall 2:
Ist der Vater des neuen Knotens schwarz, so tritt der zweite Fall ein. In diesem Fall könnte der Gedanke aufkommen, dass die fünfte Eigenschaft, also dass der Baum auf allen Pfaden von der wurzel zu den Blättern die gleiche Schwaarztiefe besitzt. Da allerdings ein schwazknoten( Nil ) beim einfügen gelöscht wird bleibt die Schwarztiefe im Baum erhalten und es ist nichts weiter zu tun.
insertCase2( Knoten n )
if n.parent.color is BLACK
return
else insertCase3( n )
- Fall 3:
Ab dem Fall drei beginnent, kann davon ausgegangen werden, dass der einzufügende Knoten einen Großvater besitzt, da der Vater rot sein muss ( sonst wäre bereits Fall eins oder Fall zwei eingetreten ) und damit nicht die Wurzel sein kann. Somit beschreibt der dritte Fall die Situation, dass sowohl der Onkel als auch der Vater rot sind. Da durch das Anhängen eines weiteren roten Knotens nun die Eigenschaft verletzt wird, dass ein roter Knoten immer zwei schwarze Kindknoten haben muss, werden der Onkel sowie der Vaterknoten schwarz und der Großvater rot gefärbt. Mit diesem Verfahren sowie der Hilfe der Verfahren von Fall eins und Fall zwei verschiebt man das Problem also soweit nach oben bis es sich auflöst, andernfalls betrachtet man einen neuen Fall.
insertCase3( Knoten n )
if uncle( n ) not null and uncle( n ).color is RED
n.parent = BLACK
uncle( n ).color = BLACK
grandparent( n ).color = RED
insertCase1( n )
else insertCase4( n )
- Fall 4:
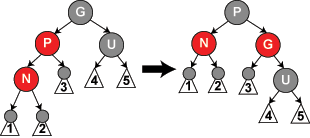
Der nächste Fall betrachtet die Situation, dass der Onkel des neuen Knotens schwarz ist( kann also auch Nil sein ) und der neue Knoten das rechte Kind seines roten Vaters ist, welcher jedoch links an seinem Größvater sitzt. Analog dazu kann der neu einzufügende Knoten auch das linke Kind seines roten Vaters sein, welcher rechts an seinem Großvater angebracht ist. Im ersten der beiden Fälle wird eine Linksrotation und im zweiten eine Rechtsrotation um den Vater durchgeführt. Anschließend wird in jedem Falle der fünfte und damit letzte Fall überprüft.
insertCase4( Knoten n )
if n is n.parent.right and n.parent is gradnparent( n ).left
rotateLeft( n.parent )
n = n.left
else
if n is n.parent.left and n.parent is gradnparent( n ).right
rotateRight( n.parent )
n = n.right
insertCase5( n )
- Fall 5:
Der letzte Fall beinhaltet die Situationen, dass der neue Knoten einen schwarzen Onkel hat( auch Nil ist schwarz ) und der linke Knoten seines Vaters ist, der sich ebenfalls links am Großvater befindet bzw. dass der neue Knoten rechts an seinem Vater hängt, der sich ebenfalls am Großvater befindet. Da in diesem Fall die Eigenschaft verletzt ist, dass der Vater des neuen knoten keine zwei schwarzen Kinder aufweisen kann, bedient man sich einer Rechtsrotation, sofern der neue Knoten links an seinem Vater ist und sich dieser links am Großvater befindet. Im entgegengesetztem Fall bedient man sich der Linksrotation um den Großvater. Anschließend wird der ehemalige Vater schwarz und der ehemalige Großvater rot gefärbt.
insertCase5( Knoten n )
n.parent.color = BLACK
grandparent( n ).color = RED
if n is n.parent.left and n.patent is grandparent( n ).left
rotateRight( grandparent( n ) )
else rotateLeft( grandparent ( n ) )
Löschen
Ebenso wie beim Einfügen kann es duch das Löschen eines Knotens in einem Rot-Schwarz-Baum dazu kommen, dass dessen Eigenschaften verletzt werden. Um den Baum demenstprechend wieder zu orden bedient man sich folgender sech Fälle. Zur besseren Lesbarkeit wird hierbei ebenfalls die Methode zur Erlangung des Bruders implementiert.
void delete_one_child(node n)
// Bedingung: n hat höchstens ein echtes Kind (kein NIL-Knoten)
node child = is_leaf(n->right) ? n->left : n->right;
replace_node(n, child);
if n.color is BLACK)
if child->color is RED
child->color = BLACK
else
delete_case1(child)
n = null
sibling( Node n )
if n is n.parent.left
return n.parent.right
else return n.paretn.left
- Fall 1:
Der erste Fall beschreibt die Situation, dass der Konfliktknoten( n ) die Wurzel des Baumes darstellt. Da die Wurzel immer schwarz sein muss ist an dieser Stelle nichts weiter zu tun, da der schwarze Knoten( also die Wurzel ) von jedem Pfad entfernt wurde. Da die neue Wurzel ebenfalls schwarz ist bleiben alle Eigenschaften des Rot-Schwarz-Baumes erhalten.
deleteCase1( Node n )
if n.parent is null
return
else deleteCase2( n )
- Fall 2:
Im zweiten Fall wird auf die Situation eingegangen, dass der Bruder des Konfliktknotens rot ist. Tritt dieser Fall ein, so wird die Farbe vom Vater sowie vom Bruder des Konfliktknotens invertiert. Im Anschluss daran wird eine Rotation um den Vater durchgeführt, wodurch der Bruder zum Großvater des Konfliktknotens wird.
deleteCase2( Node n )
if sibling( n ).color is RED
n.parent.color = RED
sibling( n).color = BLACK
if n is n.parent.left
rotateLeft( n.parent )
else rotateRight( n.parent )
deleteCase3( n )
- Fall 3:
Sind der Vater, der Bruder und die Kinder des Bruders schwarz, so tritt der dritte Fall ein. In diesem Fall wird der Bruder rot gefärbt. Im weiteren haben jedoch noch immer alle Pfade, die durch den Vater laufen einen schwarzen Knoten weniger, woduch die Eigenschaft der gleichmäßigen Schwarztiefe verletzt wird. Um dies zu "reparieren" und die Ordnung wieder herzustellen versucht man einen der sechs Fälle anzuwenden.
deleteCase3( Node n )
if n.parent.color is BLACK and
sibling( n ).color is BLACK and
sibling( n ).left.color is BLACK and
sibling( n ).right.color is BLACK
do
sibling( n ).color = RED
deleteCase1( n.parent )
else do
delelteCase4( n )
- Fall 4:
Der vierte Fall beinhaltet den Sachverhalt, dass der Bruder sowie die Kinder schwarz sind, der Vater jedoch eine rote Farbe beinhaltet. Um in diesem Fall die Ordnung wieder herzustellen ist es ausreichend dem Vater die Farbe des Bruders( schwarz ) und dem Bruder die Farbe des Vaters( rot ) zuzuweisen. Durch dieses Verfahren bleibt die Anzahl der schwarzen Knoten die nicht durch den Konfliktknoten führen gleich. Da aber auf allden Pfaden, die duch den Konfliktknoten führen ein schwarzer Knoten eingefügt wird wird das Gleichgewicht wieder hergestellt.
deleteCase4( Node n )
if n.parent.color is RED and
sibling( n ).color is BLACK and
sibling( n ).left.color is BLACK and
sibling( n ).right.color is BLACK
do
sibling( n ).color = RED
n.color = BLACK
else deleteCase5( n )
- Fall 5:
Der fünfte Fall trifft auf zwei Sachverhalte zu, die sich lediglich durch ihre Ausrichtung unterscheiden. Zum einen ist dies, dass das linke Kind des Bruders rot und das rechte Kind sowie der Bruder des Konfliktknotens schwarz sind. Der Konfliktknoten ist hierbei das linke Kind seines Vaters. Der zweite Fall stellt also somit die Situation dar, dass das rechte Kind des Bruders rot und das linke Kind sowie der Bruder schwarz sind. In diesem Fall ist der Konfliktknoten das rechte Kind seines Vaters. Um in diesem Fall die Ordnung zu wahren wird bei der ersten Möglichkeit des fünften Falles eine Rechts- und bei der zweiten dem entsprechend eine Linksrotation um den Bruder durchgeführt. Das linke bzw. das rechte Kind des Bruders wird dabei dessen neuer Vater und dieser wird Bruder des Konfliktknotens. Zudem werden die Farben des Bruders und des neuen Vaters getauscht. Zwar haben alle Pfade noch die gleiche Anzahl an schwarzen Knoten wie vorher jedoch hat der Konfliktknoten nun einen schwarzen Bruder der rechts bzw. links ein rotes Kind hat. Damit ist die Voraussetzung für den sechsten Fall gegeben ohne dass der Konfliktknoten noch der Vater beeinflusst wurden.
deleteCase6( Node n )
if n is n.parent.left and
sibling( n ).color is BLACK and
sibling( n ).left.color is RED and
sibling( n ).right.color is BLACK
do
sibling( n ).color = RED
sibling( n ).left.color = BLACK
rotateRight( sibling( n ) )
else
if n is parent.right and
sibling( n ).color is BLACK and
sibling( n ).left.color is BLACK and
sibling( n ).right.color is RED
do
sibling( n ).color = RED
rotateLeft( sibling( n ) )
deleteCase6( n )
- Fall 6:
Der letzte Fall fordert, dass der Bruder des Konfliktknotens schwarz, das Rechte Kind des Bruders rot ist. Zudem soll der Konfliktknoten das linke Kind seines Vaters sein. Aquivalent dazu ist auch die Möglichkeit, dass das linke Kind des Bruders rot ist und der Konfliktknoten das rechte Kind seines Vaters ist. Hierbei würden dann jeweils eine Links- bzw. eine Rechtsrotation um den Vater des Konfliktknotens stattfinden, wodurch der Bruder zum Großvater des Konfliktknotens wird und der Bruder wird Vater des ehemaligen rechten bzw. linken Kindes des Konfliktknotens. Im weiteren wird die Farbe des Bruders mit der Farbe des Vaters( jeweils vom Konfliktknoten ) getauscht. Das rechte bzw. das linke Kind wird schwarzgefärbt. Zu beachten ist, dass der noch immer die selbe Farbe in der Wurzel hat, wodurch die vierte Eigenschaft, dass wenn ein Knoten rot ist beide Kinder schwarz sein müssen, erhalten bleibt. Allerdings hat der Konfliktknoten einen weiteren schwarzen Vorfahren. Um diesen Sachverhalt näher zu analysieren verdeutlichen wir, dass der Vater falls er vor der Transformation nicht schwarz war er es anschließend ist. War der Vater vor der Transformation bereits schwarz, so ist er es anschließend immernoch und er hat seinen ehemaligen Bruder nun als schwarzen Großvater. Somit beinhalten die Pfade, die duch den Konfliktknoten verlaufen einen zusätzlichen Schwarzen Knoten. Für die Pfade, die den Konfliktknoen nicht enthalten ergeben sich nun zwei möglichkeiten. Zum einen kann dieser Pfad duch den Bruder des Konfliktknotens verlaufen, in diesem Fall verliefe der Pfad vor und nach der Transformatation durch den alten Bruder sowie den neuen Vater des Konfliktknotens. In diesem Falle hätten die beiden Knoten lediglich ihre Farbe vertauscht, was zur Folge hätte, dass sich an der Schwarztiefe dieses Pfades nichts ändert. Zum anderen kann es allerdings auch sein, dass der Pfad duch den neuen Onkel, welcher das rechte bzw. das linke Kind des Bruders ist, des Konfliktknotens verläuft. Das bedeutet, dass der Pfad nach der Transformation nicht mehr duch den Bruder, dessen Vater sowie dem rechten bzw. dem linken Kind des Bruders verläuft, sondern stattdessen nur noch durch den Bruder, der nun die Farbe seines alten Vaters besitzt, sowie durch das rechte bzw. linke Kind des Bruders, dessen Farbe duch die Transformation von rot auf schwarz gewechselt hat. Beide Fälle verändern somit nichts an der Anzahl der schwarzen Knoten auf den Pfaden wodurch das Gleichgewicht wieder hergestellt ist.
deleteCase6( Node n )
sibling( n ).color = n.parent.color
n.parent.color = BLACK
if n is n.parent.left do
sibling( n ).right.color = BLACK
rotateLeft( n.parent )
else do
sibling( n ).left.color = BLACK
rotateRight( n.parent )
Applet-Link
http://www.ece.uc.edu/~franco/C321/html/RedBlack/redblack.html
2-3-4-Bäume
Eigenschaften
- Knoten enthalten bis zu 3 Schlüssel
- 3-Knoten mit 3 ausgehenden Verkettungen sind zugelassen
- 4-Knoten mit 4 ausgehenden Verkettungen sind zugelassen
- Binärbaum Eigenschaften vorhanden (2-Knoten)
Suchen eines Elements
Beim Suchen in 2-3-4-Bäumen wird die Top-Down-Methode verwendet. Dabei wird ausgehend von dem kleinsten Element des Wurzelknotens, den entsprechenden Verkettungen bis zum gesuchten Schlüssel gefolgt. Im ersten Schritt wird dabei der gesuchte Schlüssel mit dem aktiven Element verglichen. Liefert der Vergleich eine wahre Aussage ist schon an dieser Stelle die Suche beendet. Ist dies nicht der Fall wird geprüft, ob der gesuchte Schlüssel kleiner ist als das aktive Element im aktuellen Knoten. Ist dieses Kriterium wahr geht man die Verkettung vor dem aktiven Element weiter entlang und setzt das kleinste Element des Kindknotens als neues aktives Element und beginnt wieder im ersten Schritt. Im Fall, dass das Kriterium nicht erfüllt ist wird im Wurzelknoten das nächstgrößere Element aktiviert und beginnt mit diesem wieder bei Schritt eins. Sollte kein nächstes Element im aktuellen Knoten vorhanden sein wird der Verkettung nach dem zuletzt aktiven Elements zum kleinsten Element des Kindknotens gefolgt und der Erste Schritt wieder ausgeführt.
Einfügen eines Elements
Günstiger Fall
Beim Einfügen wird ein Knoten solange aufgefüllt, bis er 3 Elemente enthält. Soll noch ein viertes Element aufgenommen werden ist dies nur durch ein Spalten des Knotens möglich. Dabei wird der überfüllte Knoten in 3 Teile gesplittet:
- Knoten mit zwei Elementen
- Knoten mit einem Element
- Mittleres Element
Das mittlere Element rutscht bei der Spaltung in den Elternknoten und stellt somit die Verkettung der zwei neuen Knoten dar.
Ungünstiger Fall
Muss der überfüllte Knoten wie im Günstigen Falle gespalten werden und der Elternknoten ist schon mit 3 Elementen belegt, wird das Spalten in Richtung Wurzel solange nach oben gereicht bis man entweder auf kein 4-Knoten mehr trifft oder auf die Wurzel stößt. Bei der Wurzel wird jedoch nach gleicher Aufteilungsregel eine neue Wurzel erzeugt, wenn diese ebenfalls schon voll besetzt ist.
Laufzeit: $O$(log n)
Split-Operation
Eine alternative Möglichkeit um dem ungünstigen Fall sofort vorzubeugen ist die Split-Operation. Dabei wird anders als bei den oben beschriebenen Methoden, während ein Element in den Baum eingefügt wird beim Durchlauf zusätzlich nach 4-Knoten gesucht, die daraufhin ausgepalten werden. Somit wird die Split-Operation im schlimmsten Fall einmal durchgeführt.
Löschen eines Elements
Das Löschen eines Elements aus einem Knoten lässt sich immer auf das Löschen eines Elements in einem Blatt zurückführen. Dafür ist es zunächst nötig die Position des zu löschenden Elements zu wissen. Neben dieser Position i wird außerdem das Element benötigt, welches sich an der äußersten rechten Stelle befindet um beide Elemente zu tauschen. Nun kann das Element aus dem Blatt gelöscht werden, wobei drei Fälle zu unterscheiden sind:
- mehr als ein Element im Blatt - einfaches Entfernen
- ein Element im Blatt und Nachbarknoten mit mindestens zwei Elemente - Nachfolger des zu löschenden Elements rückt an dessen Position - Kind-Nachfolger von Nachfolger rückt an Nachfolgerposition
(beim größten Element - Vorgänger)
- nur ein Element im Blatt und Nachbarknoten - Vorgängerelement mit Nachbarelement und zu löschenden Element zusammengefügt - Element löschen
(beim kleinsten Element - Nachfolger
Applet-Link
http://www.cs.unm.edu/~rlpm/499/ttft.html
B-Bäume
Einführung
Die Datenstruktur des B-Baumes hat vor allem für Datenbanken ein große Bedeutung. Dabei stehen schnelle Zugriffszeiten und somit ein schnelles Ausführen von Operationen, welche auf die Daten zugreifen eine wichtige Rolle. Eine naive Vorstellung dabei wäre einen binären Suchbaum zu verwenden. Dieser bietet zwar einen Suchlaufzeit von $O$(log n), jedoch wäre beim Einfügen bzw. Löschen schnell klar, dass der Baum schnell entarten würde, wodurch eine schnelle Suche nicht gewährleistet wäre. Eine weitere Überlegung wäre ein höhenbalancierter Baum, wie der AVL-Baum Somit hätte man das Problem der Entartung behoben. Doch auch dies ist nicht die optimale Lösung wenn man sich den hardwaretechnischen Aspekt betrachtet. Denn da bei einem Telefonbuch zum Beispiel durch Rebalancierungsmaßnahmen keine Lokalität mehr gewährleistet ist müsste der gesamte Baum im Hauptspeicher geladen bleiben, was sich negativ auf die Laufzeit auswirkt. Daher kommt an dieser Stelle der B-Baum ins Spiel der für diese Kriterien optimal geeignet ist.
Eigenschaften
- alle Höhen von Wurzel zu Blatt immer gleich
- jeder Knoten besteht aus min. k und max. 2k Elemente
- unterschiedliche Anzahl von Elementen in Knoten möglich
- Wurzel besteht aus zwischen 1 und 2k Elementen
- Knoten mit n Elementen besitzt n+1 Verkettungen
- Blätter haben keine bzw. undefinierte Verkettungen
Suchen eines Elements
Der Suchalgorithmus arbeitet nach dem gleichen Schema, wie es bei den 2-3-4-Bäumen der Fall ist.
Einfügen eines Elements
Zunächst wird die korrekte Position zum Einfügen des Schlüssels ermittelt. Besitzt der sich an dieser Position befindende Knoten weniger als 2k Elemente erfolgt ein einfaches Einfügen des Schlüssels in den aktuellen Knoten. Befinden sich schon 2k Elemente vor dem Einfügen in dem Knoten, ist dieser Überfüllt und es wird auf die Splitting-Methode, wie bei den 2-3-4-Bäumen zurückgegriffen.
Einfügealgortithmus
Insert ( KEY )
find leaf or node L;
if ( L overflows ){
split L, push up the middle key
to parent node P;´
}
if (P overflows){
repeat the split recursively;
}
else{
add the KEY K in node L;
}
Löschen eines Elements
Beim Löschvorgang in B-Bäumen muss unterschieden werden, ob sich das zu löschende Element in einem Blatt oder Knoten befindet. So wird zum Beispiel in einem Blatt der Schlüssel einfach gelöscht. In einem Knoten hingegen wird der Schlüssel gelöscht und gegen das kleinste Element (zuerst) aus dem rechten Unterbaum ersetzt. Wird dabei ein Element, was zum Ersetzen benötigt wurde, aus einem Blatt oder Knoten so entfernt, dass es die Baumeigenschaften verletzt,(mindestens k Einträge) werden die Nachbarblätter zur Hilfe genommen. Dabei gibt es zwei Möglichkeiten:
- Blatt / Knoten weniger als k Einträge - Verschiebung der Einträge innerhalb der Nachbarblätter über den Vaterknoten)
- Nachbarblätter / Nachbarknoten zusammen kleiner oder gleich 2k Einträge - Durchführung einer "Concatention" (Verschmelzung von benachbarten Blättern - Gegenstück zum Splitting beim Einfügen)
Löschalgorithmus
delete( K )
locate key K, in node N
if( N is a non-leaf node){
delete K from N;
find the immediately largest key K1;
copy K1 in the old position of K;
invoke this DELETION routine on K1 from leaf node L;
else{
if( N underflows ){
let N1 be the brother of N;
}
if( N1 is full){
borrow a key from N1
THROUGH the parent node;
}else{
MERGE: pull the key from the parent P,
and merge it with the keys of N and N1
into a new node;
if( P underflows){
repeat recursively
}
}
}
Wahl von k
Die Wahl der Anzahl der möglichen Einträge eines Knotens hängt von der verwendeten Hardware ab. Das beinhaltet den Zugriff auf den Hintergrundspeicher und die Größe des Arbeitsspeichers. Dabei ist das Ziel auf geringe Zugriffszeiten auf den langsamen Hintergrundspeicher gerichtet. Ein weiterer wichtiger Punkt ist, dass je mehr Einträge in einem Knoten aufgenommen werden können, desto flacher wird der Baum. Im Bezug auf den Hintergrundspeicher bedeutet das, weniger Zugriffe. Der Nachteil dabei ist, dass mit steigendem k die Zugriffe länger dauern. Des weiteren muss beachtet werden, das der Arbeitsspeicher die Knotengröße begrenzt. Wie man erkennen kann steht die Wahl von k mit verschiedenen Faktoren in Verbindung. Daher muss k individuell für jedes System ermittelt werden.
B*-Bäume
Eigenschaften
- alle Höhen von Wurzel zu Blatt immer gleich
- jeder Knoten hat max. 2k Elemente und ist zu 2/3 aufgefüllt
- unterschiedliche Anzahl von Elementen in Knoten möglich
- Wurzel besteht aus zwischen 1 und 2k Elementen
- Knoten mit n Elementen besitzt n+1 Verkettungen
- Blätter haben keine bzw. undefinierte Verkettungen
Vergleich B-Bäume und B*-Bäume
Vorteile:
Sind Knoten minimaler besetzt, haben die Knoten von B*-Baum weniger Söhne als die von B-Bäumen. Sind alle Knoten minimal besetzt(worst-case), ist die Höhe der B*-Bäume geringer als die von normalen B-Bäumen. Hinzukommt, dass B*-Bäume eine bessere Speicherauslastung garantieren.
Nachteile:
Bei sehr stark befüllten Knoten (z.B. mindestens 2k-1 Einträge in einem B*-Baum), kommt es mit einer sehr hohen Wahrscheinlichkeit zu einem Nachteil in Einfüge-Operationen, da man vermehrt auf volle Knoten treffen würde. Dies würde bei jedem vollen Knoten ein Splitting mit sich bringen, welches sich oft rekursiv bis zur Wurzel fortsetzen würde. Daher laufen bei B*-Bäume die Operationen weniger lokal ab als bei B-Bäumen. Hinzukommen außerdem die generell aufwendigeren Operationen.
B+-Bäume
Punktsuche und Bereichssuche
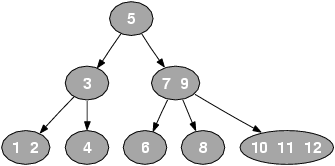
Die Punktsuche beschreibt die normale Suchfunktion in einem Baum (z.B. Binär-Baum). Im Gegensatz dazu wird bei der Bereichssuche nicht nur einem Element gesucht, sondern nach mehreren Datenwerten durch deren Schlüssel, welche hintereinander geordnet sind.
Eigenschaften
- Knoten haben max. drei Schlüssel mit max. vier Pointern
- Wurzel hat min. ein Wert mit zwei Pointern
- innere Knoten min. ein Schlüssel mit zwei Pointern
- Blätter haben min. zwei Schlüssel mit drei Pointern
- Verkettung der Blätter von links nach rechts
- Nutzerdaten nur in Blättern enthalten
next()-Operation
Die next()-Operation ist ebenfalls eine Suchoperation wodurch Blattinhalte geladen werden können. Gerade in dieser Operation kommt der Vorteil von B+- gegenüber B-Bäumen zum Vorschein. Denn anders als beim B-Baum, bei dem man nachdem ein Blatt gefunden wurde erst zu dem Vaterknoten zurückkehren muss um zum nächsten Nachbarknoten zu gelangen (Vaterknoten mehr als ein mal besucht - höherer Aufwand), nutzt der B+-Baum einen zusätzlichen Pointer zwischen den einzelnen Blättern von links nach rechts. Dadurch können die verschiedenen Einträge sequentiell eingelesen werden.
Parallele Operationen
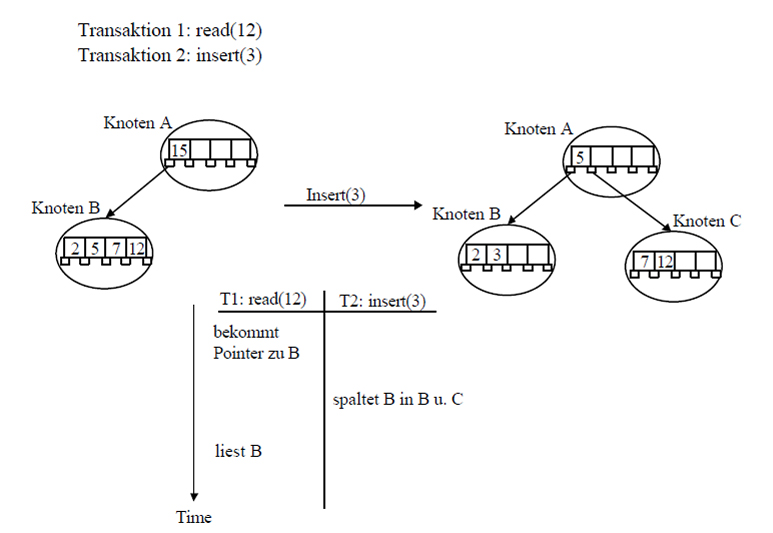
In einer Multiuserumgebung kann es durch Parallele Operationen zu Problemen kommen, da wie im Beispiel unten dargestellt ist könnten zwei User gleichzeitig Operationen an einen Baum übergeben. Wenn zum Beispiel jemand nach einem Element sucht, ein anderer jedoch eine Element so einfügt das der Knoten in dem gerade gesucht wird gesplittet wird, kann das Element nicht gefunden werden, obwohl es im Baum vorhanden ist.
Die Lösung für das Problem der parallelen Zugriffe besteht in koordinierten Zugriffen. Das bedeutet es muss durch ein Protokoll geregelt werden, wann welche Operationen gleichzeitig ausgeführt werden dürfen. Zum Beispiel das mehrere Suchen gleichzeitig stattfinden dürfen, da diese sich in keinster Weise behindern. Geht es um das Einfügen oder Löschen von Elementen, muss man sich nach der Einstufung der Knoten in sicher oder unsicher richten. Dadurch könnte man dann festlegen ob Knoten, wenn sie zum Beispiel unsicher sind für Einfüge- oder Lösch-Operationen blockiert sind um eine Such-Operation nicht zu stören. Erst wenn keine Suche mehr auf einem Knoten läuft wird dieser dann wieder freigegeben.
(un)sichere Knoten
Ob ein Knoten sicher oder unsicher ist hängt von seinen Einträgen und den parallelen Operationen ab. Ein Knoten, der zum Beispiel mit 2k Elementen gefüllt ist stellt im Bezug auf eine insert()-Operation ein unsicheren Knoten dar, da ein Einfügen ein Splitting mit sich bringen würde. Hingegen ein Knoten mit weniger als 2k Element stell ein sicheren Knoten dar, da er bei einem insert() nicht gesplittet wird. Dies trifft ebenfalls beim Löschen zu wenn nur k Elemente im Knoten vorhanden sind. Dann handelt es sich um einen unsicheren Knoten, da es eine "Concatenation" bewirken würde und somit sogar Auswirkungen auf den Vaterknoten hätte. Sicher ist der Knoten deshalb erst wenn er mehr als k Elemente bei einem delete() aufweist.
Applet-Link
http://slady.net/java/bt/view.php
Literatur
- TU-München Hauptseminar Informatik 2001/2002 Prof.R.Bayer B-Bäume
- Algorithmen - Eine Einführung 2. Auflage Th.H.Cormen | Ch.E. Leiserson | R.Rivest | C.Stein (Oldenbourg)
- Robert Sedgewick - Algorithmen (Addison-Wesley)
- http://www.mathematik-netz.de/pdf/AVL.pdf