Sortieren und Suchen WS13-14

Aus ProgrammingWiki

< AuK
Wechseln zu: Navigation, Suche

Loading

Inhaltsverzeichnis

Sortieren

Einführung

Das Sortieren ist eines der am häufigsten auftretenden Probleme in der Informatik und ein fundamentales Problem in der Arbeit mit Algorithmen. Einige Anwendungen können nur mit sortierten Daten arbeiten oder verwenden das Sortieren als Unterprogramm. Im Jahr 1987 wurde laut einer Aussage von IBM 25 % der Rechenzeit in den Rechenzentren allein durch Sortieren verbraucht.
Im Folgenden sollen nur interne Sortiermethoden vermittelt werden, bei denen die Daten (z.B. in einem Feld) abgespeichert werden können. Es werden Dateien sortiert, welche aus mehreren Datensätzen bestehen. Dabei bestehen die Datensätze aus Informationen und Schlüsseln. Da die Informationen in den Sortiermethoden keine Rolle spielen, werden diese in der Betrachtung komplett vernachlässigt. Um sich auf die Arbeitsweise der Algorithmen konzentrieren zu können vereinbart man, dass die Schlüssel zunächst nur durch ganze Zahlen dargestellt werden.
Es werden sowohl elementare Sortiermethoden vorgestellt, welche für kleine Dateien oder für spezielle Strukturen genutzt werden und die Grundlage für komplexere Algorithmen bilden, als auch komplexere Sortiermethoden, welche es z.B. erlauben komplexere Schlüssel zu sortieren.

Elementare Sortierverfahren

Selection Sort

Selection Sort (Sortieren durch Auswählen) wählt wiederholt das kleinste Element im Feld aus.

Ablauf
Man sucht das kleinste Element im Feld und tauscht es mit dem an der ersten Stelle befindlichen Element. Im nächsten Schritt wählt man das zweitkleinste Element und tauscht es mit dem Element an der zweiten Stelle aus. Dieser Vorgang wird so oft wiederholt bis das komplette Feld durchlaufen wurde, denn genau dann ist das Feld sortiert.

Leistungsfähigkeit
Selection Sort besitzt im Worst-Case und im Average-Case einen quadratischen Aufwand $\mathcal O(n^2)$. Die Ausführung dieses Verfahrens benötigt keinen zusätzlichen Speicherplatz. Der Durchlauf benötigt ca. $\frac{n^2}{2}$ Vergleiche und $n$ Austauschoperationen, da für jedes Feld von $1$ bis $n-1$ jeweils $1$ Austausch und insgesamt $(n-1)+(n-2)+...+2+1$ Vergleiche notwendig sind. Dies ist jedoch unabhängig von den Eingabedaten, abhängig ist nur die Anzahl der Wechsel des Wertes der Variable minimum. Im Average-Case liegt die Laufzeit der Anzahl der Wertwechsel in $\mathcal O(n \log n)$, so dass man sagen kann, dass die Laufzeit von Selektion Sort relativ unempfindlich gegenüber den Eingabedaten ist.

Insertion Sort

Insertion Sort (Sortieren durch Einfügen) ist flexibler als Selection Sort.

Ablauf
Man betrachtet ein Element nach dem anderen und fügt jedes Element an seinem Platz zwischen den bereits betrachteten Elementen (links von ihm) ein. Das Einfügen wird durch Verschieben der größeren Elemente nach rechts realisiert. Das Feld ist vollständig sortiert, wenn das rechte Ende des Feldes erreicht wurde.

Leistungsfähigkeit
Die Laufzeit des Insertion Sort ist abhängig von Inversionen. Inversionen beschreiben den Abstand eines Elementes von dessen Postion nach der Sortierung. Um diesen Abstand zu bestimmen zählt man die Anzahl der Elemente mit einem höheren Wert links vom betrachteten Element. Im Best-Case besitzt das Verfahren eine Laufzeit von $\mathcal O(1)$, da das Feld nur einmal durchgegangen werden muss um festzustellen, dass es bereits sortiert ist. Im Average-Case benötigt das Verfahren ca. $\frac{n^2}{4}$ Vergleiche und $\frac{n^2}{8}$ Austausche. Im Worst-Case verdoppeln sich diese Anzahlen.

Bubble Sort

(Sortieren durch Austauschen)

Ablauf
Man durchläuft das Feld immer wieder und tauscht benachbarte Elemente, wenn nötig. Das Feld ist sortiert, wenn in einem Felddurchlauf kein Austausch mehr nötig ist.

Leistungsfähigkeit
Bei diesem Verfahren ist die Laufzeit abhängig von den Eingabedaten.

  • Im Best-Case beträgt sie $1$, da nur ein Durchlauf benötigt wird um zu erkennen, dass die Daten bereits sortiert sind.
  • Im Worst-Case werden $\frac{n^2}{2}$ Vergleiche und ebenso viele Austauschoperationen benötigt.
  • Der Average-Case arbeitet nicht wirklich besser als der Worst-Case, eine genaue Analyse ist jedoch schwierig.

Shellsort

Shellsort ist eine Art Erweiterung von Insertion Sort, wobei auch der Tausch von weit entfernten Elementen ermöglicht wird. Die Elemente werden so umsortiert, dass ein sortiertes Feld vorliegt, wenn man jedes h-te Element entnimmt. Man nennt dies h-sortiert. Das so entstandene Feld besteht aus $h$ unabhängig sortierten Teilfeldern, welche sich überlagern. Das Sortieren von großen $h$ verringert die Durchläufe für kleine $h$. Diese Prozedur wird mit einer beliebigen Zahlenliste ausgeführt, wobei die Liste mit 1 enden muss.

Ablauf
Würde eine Datei mit der Zahlenfolge $1093,364,121,40,13,4,1$ sortiert werden, so müsste man folgendermaßen vorgehen:
Zuerst würde man jede $1093.$ Zahl miteinander vergleichen und sortieren, d.h. die Zahlen an Position $0,1093,2196..$ ebenso an den Positionen $1,1094,2197..$ werden (z.B. mittels Insertion Sort) sortiert. Im zweiten Schritt würde man jede $364.$ Zahl miteinander vergleichen und somit die Zahlen an den Positionen $0,364,728,1092..$ sortieren. Im dritten Schritt würde man jede $121.$ Zahl vergleichen, d.h. die Zahlen an den Positionen $0,121,242,363..$ sortieren. Und ebenso würde man nun noch für $40,13,4$ und $1$ verfahren.

Leistungsfähigkeit
Eine feste Effizienz von Shellsort kann nicht bestimmt werden, da diese abhängig von den gewählten Zahlenfolgen ist. Es wird jedoch davon abgeraten die Zahlenfolge abhängig von der Anzahl der Datensätze festzulegen, da dies für einige Werte von $n$ zu schlechten Folgen führen kann.

Distribution Counting

(Verteilungszählen)
Für sehr spezielle Situationen:

  • "Sortiere eine Datei von $n$ Datensätzen, die nur Schlüssel enthält, deren Werte voneinander verschiedene Zahlen zwischen $1$ und $n$ sind." Für dieses Problem kann man sehr leicht einen Algorithmus angeben:

  • "Sortiere eine Datei der Größe $n$, deren Schlüssel ganze Zahlen zwischen $0$ und $m−1$ sind." Falls $m$ nicht zu groß ist, kann die Sortierung mittels Verteilungszählen realisiert werden. Dabei sind mehrere Schleifendurchgänge notwendig:
  1. Ein Feld count[] wird mit $0$ initialisiert. (Da in Java primitive Typen mit $0$ vorbelegt sind, würde dies wegfallen)
  2. Dem Wert des Feldes in count[] wird die Anzahl der jeweiligen ganzen Zahlen zugeordnet.
  3. Die Zahlen der einzelnen Werte werden aufaddiert.
Diese aufaddierten Werte können nun genutzt werden um das Eingabefeld zu sortieren. Man untersucht das Feld beginnend von hinten (wieder mittels einer Schleife) und setzt den untersuchten Wert jeweils an die Stelle im Feld, dessen Index = count[untersuchter Wert]. Danach wird der Wert von count[untersuchter Wert] dekrementiert und mit dem nächsten Wert des Eingabefeldes fortgefahren.

Digitales Sortieren

Die Schlüssel eines Datensatzes zur Sortierung können mitunter sehr komplex sein (z.B. im Telefonbuch oder einem Bibliothekskatalog). Aus diesem Grund ist es sinnvoll sich die Schlüssel als Zahlen aus einem bestimmten Zahlenbereich vorzustellen. Methoden bei denen diese Eigenschaft genutzt wird nennt man digitale Sortierverfahren (radix sorts), diese vergleichen nicht die kompletten Schlüssel, sondern sie verarbeiten und vergleichen nur bestimmte Teile von Schlüsseln. Digitale Sortierverfahren behandeln die Schlüssel von Datensätzen als Zahlen in einem bestimmten Zahlensystem $M$ (für verschiedene $M$) und bearbeiten die einzelnen Ziffern der Zahlen. Da in Computern alles als Binärcode darstellbar ist, verwendet das digitale Sortieren häufig die Zahlenbasis $2$ oder eine Potenz von $2$, denn wenn dem Nutzer die Schlüsseldaten binär vorliegen so ist die Anwendung vieler digitale Sortierverfahren möglich.

Bits

Wenn der Schlüssel als Binärzahl gegeben ist, so besteht die Grundoperation darin zusammenhängende Bits zu extrahieren. In Maschienensprachen realisiert man dies durch bitweises Anwenden von AND und durch Stellenverschiebungen.
Will man z.B. die zwei führenden Bits einer aus 10 Bits bestehenden Binärzahl extrahieren so nutzt man dazu erst die Verschiebung um acht Stellen nach rechts und dann die Anwendung von AND mit 0000000011. In Java (und weiteren höheren Programmiersprachen) hat man diese Möglichkeiten jedoch nicht, kann aber das Ergebnis des gleichen Beispiels mit (x / 256) % 4 (es gilt $x \in Z$) erreichen. Die Operation / beschreibt dabei die ganzzahlige Division. Um die zwei genannten Grundoperationen der Maschinensprache auch in anderen Programmiersprachen zu nutzen gilt im Allgemeinen folgendes:

  • Bitverschiebung um k Stellen nach rechts: $x$ / $2^k$
  • alle bis auf j Bits von rechts 0 setzen: $x\ \%\ 2^j$

Dabei ist $x$ eine ganze Zahl in dezimaler Darstellung. Um digitale Sortieralgorithmen zu schreiben, kann man sich nun leicht eine Prozedur schreiben welche diese beiden Operationen vereint.

Im folgenden soll nun eines von zwei digitales Suchverfahren behandelt werden, welche sich in der Reihenfolge der Bituntersuchung unterscheiden.

Radix Exchange Sort

(digitales Austausch-Sortierverfahren)
Radix Exchange Sort untersucht die Bits in ihrer Reihenfolge von links nach rechts. Das Ergebnis des Vergleiches zwischen Schlüsseln nimmt nur den Wert des Bits in der ersten Unterscheidungsstelle an. Man geht davon aus, dass die Daten so sortiert werden, dass ein Schlüssel mit führendem Bit 0 vor einem Schlüssel mit führendem Bit 1 kommt. Man kann eine rekursive Sortiermethode entwickeln, so dass eine unabhängige Sortierung der Teildaten dazu führt das auch die Datei sortiert ist.
Dabei durchsucht man die Datei von links, bis man einen Schlüssel mit führendem Bit 1 gefunden hat und von rechts, bis man einen Schlüssel mit führendem Bit 0 gefunden hat und tauscht die zwei dazugehörigen Datensätze miteinander aus. Diesen Vorgang wiederholt man so lange, bis die linke und rechte Seite sich beim Durchgehen treffen. Danach setzt man den Vorgang für die jeweiligen Bereiche (mit führender 0, mit führender 1) erneut fort bis alle Bits sortiert wurde.

Eine mögliche Implementation könnte folgendermaßen aussehen:

Prioritätswarteschlangen

Oft müssen zunächst viele Datensätze gesammelt werden und ab einem bestimmten Zeitpunkt soll der größte Datensatz verarbeitet werden und danach der zweitgrößte usw.. Eine Datenstruktur in welcher solche Operationen möglich sind muss also sowohl das Einfügen eines neuen Elements als auch das Löschen des größten Elements unterstützen. Eine Datenstruktur vergleichbar mit Stapel (wo das neueste Element gelöscht wird) und Schlange (wo das älteste Element gelöscht wird) nennt man Prioritätswarteschlange (priority queue). Prioritätswarteschlangen sind dabei Verallgemeinerungen von Stapeln oder Schlangen, da man diese Datenstrukturen durch geeignete Verteilung der Prioritäten implementieren kann. Diese Datenstruktur bildet einen grundlegenden Baustein für weiterentwickelte Algorithmen, hauptsächlich weil sie sehr flexibel ist und viele verschiedene Mengenoperationen mit ihrer Hilfe angewendet werden können. Prioritätswarteschlangen sind Datenstrukturen, welche numerische Schlüssel (sogenannte Prioritäten enthalten). Es gibt sieben grundlegende Operationen, welche zur Erstellung und Bearbeitung von Prioritätswarteschlangen notwendig sind:

  • construct - Aufbauen einer Prioritätswarteschlange aus $n$ Elementen
  • insert - Einfügen eines neuen Elements
  • remove - Entfernen des größten Elements
  • replace - Ersetzen des größten Elements durch ein neues (außer das neue Element ist größer)
  • change - Verändern der Priorität eines Elements
  • delete - Löschen eines beliebigen vorhandenen Elements
  • join - Zusammenfügen von zwei beliebig langen Prioritätswarteschlangen

Einige dieser Operationen sind ebenso durch Kombination zweier anderer Operationen darstellbar, jedoch ist die direkte Nutzung effizienter, wenn höhere Datenstrukturen für die Implementation genutzt werden. Will man sich jedoch auf die klassische Datenstruktur heap konzentrieren, so sind nur fünf der oben genannten Operationen direkt implementierbar. Unterschiedliche Implementationen der Prioritätswarteschlange können sich in der Leistungsfähigkeit einzelner Operationen unterscheiden, was sich wiederum in den Kosten widerspiegelt.

Elementare Implementationen

Es gibt zwei grundlegende Methoden, mit denen die Prioritätswarteschlange implementiert werden kann: die ungeordnete Liste und die geordnete Liste. Bei beiden Methoden unterscheiden sich die Laufzeiten für verschiedene Operationen und somit muss durch den Anwendungsfall entschieden werden, welche Implementation besser geeignet ist.

ungeordnete Liste geordnete Liste
int[$0..n$] array ohne Beachtung der Schlüsselreihenfolge int[$0..n$] array mit wachsender Schlüsselreihenfolge
insert konstante Laufzeit maximal lineare Laufzeit
remove lineare Laufzeit konstante Laufzeit
replace lineare Laufzeit konstante Laufzeit
change konstante Laufzeit konstante Laufzeit
Benutzung ähnelt Selection Sort Insertion Sort
Anwendungsgebiete wenige remove-Operationen nötig, viele insert-Operationen insert-Operationen liegen nahe dem größten Element

Eine Möglichkeit der Implementation eines ungeordneten Feldes als Array könnte folgendermaßen aussehen:

Heap

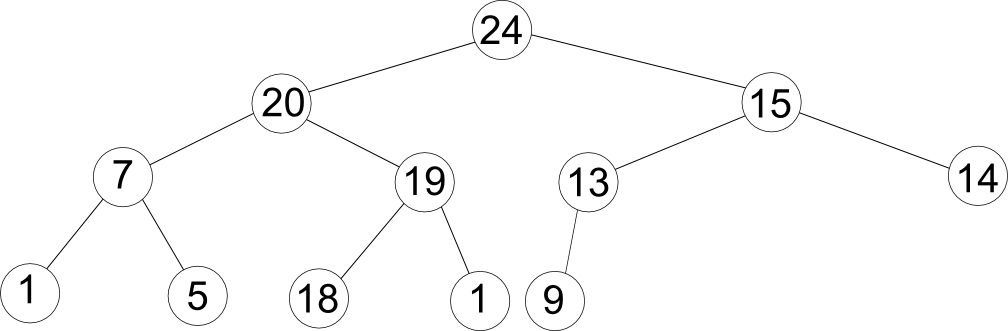
Um die Operationen der Prioritätswarteschlange zu verwenden müssen wir eine Datenstruktur verwenden von der bekannt ist, dass ein Schlüssel jeweils größer ist als zwei andere Schlüssel. Dies könnte man in einer Baumstruktur darstellen, wobei die jeweiligen Kindknoten eines Knoten die zwei bekannten kleineren Elemente des Schlüssels sind (vollständig binärer Baum). Die beiden Knoten unter jedem Knoten sind dabei dessen direkten Nachfolger und der Knoten über ihm ist sein direkter Vorgänger. Für die einzelnen Knoten des Baumes soll nun jedoch die Heapbedingung gelten:

Der Schlüssel in jedem Knoten soll größer sein als die Schlüssel in seinen Nachfolgern.

Aus dieser Bedingung kann man ableiten, dass das Element mit dem größten Schlüssel die Wurzel bildet.

S3damuel Heap.png

Bis jetzt haben wir die Prioritätswarteschlange als Feld implementiert. Dabei wird das Feld an der Stelle $0$ mit dem Schlüssel der Wurzel belegt und alle weiteren Felder werden entlang der Höhen von links nach rechts belegt. Damit entsteht für den oben gezeigten Baum folgendes Array:

k 1 2 3 4 5 6 7 8 9 10 11 12
a[k] 24 20 15 7 19 13 14 1 5 18 1 9

Nutzt man diese Umwandlung von einem Baum zu einem Feld so ist es sehr leicht Vorgänger und Nachfolger für einen bestimmten Knoten zu finden.
Gegeben ist der Knoten $j$. Seinen Vorgänger findet man am Index $2 / j$ und seine Nachfolger befinden sich auf den Positionen $2j$ und $2j+1$. Auf allen Pfaden im Heap (mit $n$ Knoten) befinden sich ca. $\lg n$ Knoten, da sich auf der untersten Ebene ca. $\frac{n}{2}$ Knoten befinden, auf der darüber ca. $\frac{n}{4}$ usw., daraus ergibt sich das jede Operation mit Prioritätswarteschlangen bei Verwendung von Heaps in $\mathcal O(\lg n)$ ausgeführt werden können.

Implementationen mit Heaps

Algorithmen für Prioritätswarteschlangen laufen alle so ab, dass sie eine Strukturänderung des Heaps durchführen und danach absichern, dass die Heapbedingung wieder gegeben ist, in dem sie ihn modifizieren.

Um einen Heap erstellen zu können ist eine Operation insert(key) notwendig, welche das Feld um einen Datensatz vergrößert und in den neuen Datensatz den Schlüssel einfügt. Sollte dieser Knoten jedoch größer als sein Vorgänger sein, so wäre die Heapbedingung verletzt, also muss sie wieder hergestellt werden. Diese Wiederherstellung kann mittels einer kleinen Operationen, welche den Heap von unten nach oben durchgeht, gewährleistet werden:

Im obigen Code beschreibt das Array heap das Feld auf dem die Operationen ausgeführt werden.

Für andere Anwendungen, z.B. nach der Anwendung der Operation replace(key), ist es jedoch notwendig, den Heap von oben nach unten zu überprüfen, da das Wurzelelement getauscht wurde. Man kann dafür folgende Operation nutzen:

Bei der von der Prioritätswarteschlangen bekannten change(pos,key) Operation muss je nach Veränderung der Priorität entschieden werden. Wird die ehemalige Priorität erhöht, so muss upheap(k) aufgerufen werden, im anderen Fall downheap(k).

Heapsort

Heapsort ist ein Sortierverfahren, welches in ca. $m \log m$ Schritten ein sortiertes Ergebnis liefert, unabhängig von den Eingabedaten. Allerdings ist dieses Verfahren nur halb so schnell wie Quicksort. Bei diesem Verfahren beschreibt nun $m$ die Anzahl der zu sortierenden Elemente und $n$ weiterhin die Größe des Heaps.

Ablauf
Die Sortierung erfolgt grundlegend in zwei Schritten:

  1. Aufbau des Heaps
  2. Abbau des Heaps in sortierter Reihenfolge.

Der Aufbau des Heaps besteht aus $m$-maligen Aufruf von insert(key) in den Heap. Aufgrund der Heapbedingung, steht am Ende dieser inserts das größte Element als Wurzelelement bzw. im Feld an Stelle $0$. Nun werden nacheinander die Elemente wieder aus dem Heap entfernt: nach der Entfernung eines Elementes rückt das letzte Element des Baumes an die Stelle der Wurzel und die Heapbedingung wird wieder hergestellt. Danach kann das nächste Element entfernt werden.


Mergesort

Mergsort ist ein rekursiver Algorithmus, welcher als Grundlage die Operation Mischen (merging) besitzt. Diese Operation nimmt zwei sortierte Dateien und fügt sie zu einer großen sortierten Datei zusammen, man kann sie vergleichen mit dem sogenannten Reißverschlussverfahren auf Straßen, nur dass an dieser stelle jeweils das kleinere Auto aus jeder Schlange zuerst fahren dürfte und nicht zwingend immer abwechselnd. Mergesort hat allerdings einen hauptsächlichen Nachteil, es benötigt zum Sortieren von $n$ Datensätzen einen zu $n$ proportionalen Speicherplatz. Es eignet sich allerdings gut für Situationen, in denen die Geschwindigkeit wesentlich ist, jedoch genügend Speicherplatz zur Verfügung steht. Ein Vorteil von Mergesort ist, dass die Zugriffe auf die einzelnen Datensätze meist sequentiell verarbeitet werden, damit kann dieser Algorithmus auch für verkettete Listen genutzt werden.

Für die Implementation von Mergesort benötigen wir das sogenannte Zweiweg-Mischen. Diese Art des Mischens erwartet zwei sortierte Dateien (a[$0..k$], b[$0..l$]) als Eingabe und gibt eine sortierte Ausgabedatei (c[$0..l+k$]) aus. Eine offensichtliche Implementation dieses Mischens ist jeweils das kleinste Element der beiden Listen als erstes in die neue Liste einzufügen.

Ablauf
Um die Elemente in einer gegebenen Datei zu sortieren teilt man sie in zwei Hälften. Diese zwei Hälften werden dann jeweils sortiert (rekursiv) und am Ende werden diese Teillisten wieder zusammengemischt.

MergeSort als Klasse


Hier eine mögliche Implementation von Mergesort als Klasse: Die Anwedung der Sortierung erfolgt durch den folgenden Aufruf in der Main:

Leistungsfähigkeit
Das Sortieren von $n$ Datensätzen benötigt ca. $n \lg n$ Vergleiche, da jeweils die Elemente in den Teilfeldern untersucht werden. Die Anzahl der Vergleich wird durch die rekurrente Beziehung $m_n=2\cdot m_{n/2}+n$ mit $m_1=0$ beschrieben. Aus ihr folgt, dass $m_n$ $n\lg n$ ca. entspricht. Für ungerade $n$ wird $\frac{n}{2}$ als ganzzahlige Division angewendet.
Der Algorithmus benötigt einen zusätzlichen Speicher welcher proportional zu $n$ ist, was leicht erkennbar in der Implementation ist.
Desweiteren ist Mergesort ein Algorithmus, welcher unabhängig gegenüber seinen Eingabedaten ist. Die Eingabe bestimmt lediglich die Reihenfolge der Verarbeitung. Die Anzahl der Durchläufe ist jedoch abhängig von der Feldgröße in den jeweiligen rekursiven Schritten.

Suchen

Einführung

Das Suchen nach Daten ist eine der wichtigsten Aufgaben eines Computers, da es weitere grundlegende Operationen wie das Ersetzen, Löschen oder Ändern von Daten erst ermöglicht. Aufgrund dieser hohen Priorität sind Suchverfahren sehr gut hinsichtlich ihres Aufwandes erforscht. Suchen ist dabei das Finden von Mustern oder Objekten mit bestimmten Eigenschaften in einem Suchraum. Beispiele sind Zeichenketten aus einem Text oder Zahlen aus einer Liste von Zahlen. Betrachtet werden auch die Datenstrukturen, auf welche die Verfahren angewendet werden können (elementare oder effizientere, wie Bäume). Außerdem ist zu prüfen, ob eine Vorsortierung des Suchraumes notwendig, effizienzverbessernd oder unnötig ist. In diesem Kapitel werden verschiedene Suchverfahren mit ihren Aufwänden vorgestellt, von einfachen schrittweisen Suchen und deren Verbesserungen hin zu komplexen Suchvorgängen in Bäumen. Es sei hierbei auf das No-free-Lunch-Theoreme verwiesen, welches besagt, dass es kein universelles Optimierungsproblem angewandt auf alle Problemmengen gibt. Für die Suchalgorithmen bedeutet dies, dass die Suchverfahren für den speziellen Anwendungszweck besser sein können als andere, nicht aber für alle Anwendungsbereiche.

Lineare Suche

Die Lineare oder sequentielle Suche ist nur (effizient) anwendbar auf kleine Suchräume und selten stattfindenen Suchoperationen. Dafür ist sie sehr leicht zu implementieren und auf unsortierte Suchräume anwendbar. Nötig ist ein Element $e$, welches mit dem Suchschlüssel $s$ verknüpft ist. Dieser kann als Attribut des Elements gewertet werden. Es wird immer nach dem Suchschlüssel gesucht! Bei Zahlen wird der Suchschlüssel meist dem Zahlenwert entsprechen, doch kann beispielsweise einem Buchstabe eine Zahl zugeordnet werden und durch Suche nach einer bestimmten Zahl erhält man den Buchstaben. Bei der Linearen Suche wird nun der Suchraum sequentiell, d.h. Element für Element, betrachtet und der Suchschlüssel mit dem Suchschlüssel des zu suchenden Elements verglichen.

Der Best-Case ist offensichtlich: Das erste Element ist das gesuchte, die Laufzeit liegt in $\mathcal O(1)$. Umgekehrt der Worst-Case, wobei keins oder das letzte Element den Suchschlüssel besitzen: $\mathcal O(n)$. Der Average-Case lässt sich ebenso leicht bestimmen: Sucherfolg bei der halben Feldlänge, also $\frac{n}{2} = 0.5\cdot n=\mathcal O(n)$. Geht man davon aus, dass jeder Datensatz gleichwahrscheinlich gesucht wird, ergibt sich für den Average-Case ebenfalls die Formel $\frac{1}{n}\cdot \sum_{i=1}^{n} i = \frac{n+1}{2}$. Das entspricht $\mathcal O(n)$.

Binäre Suche

Die Binäre Suche stellt eine Erweiterung der Linearen Suche dar. Das Ziel war es, die nötigen Vergleichsschritte zu minimieren. Angewandt wird das Verfahren bei häufigen Suchoperationen mit statischem Suchraum, da für die Binäre Suche eine Vorsortierung notwendig ist. Bei der Binären Suche wird der Suchschlüssel des Elements in der Mitte des Suchraumes zum Vergleich herangezogen. Je nach Ergebnis des Vergleiches wurde entweder das gesuchte Objekt gefunden (Laufzeit $\mathcal O(1)$) oder es wird mit einem der Teilbereiche weitergearbeitet. 

Übung: Wie viele Teilungen müssen durchgeführt werden?
Suchraum = (1,2,3,4,5,6,7,8,9,10), Suchschlüssel = 4

Beim Worst-Case muss solange geteilt werden, bis nur noch ein Element im Suchraum vorhanden ist. Wichtigster Teil der Binären Suche ist das Halbieren des Suchraumes, was auch rekursiv definiert werden kann. Mit Hilfe der rekurrenten Beziehung $C_n=C_{n/2}+1\approx \lg n$ mit $C_1=0$, ergibt sich für das Binäre Suchen eine Laufzeit in $\mathcal O(\lg n)$. Ist $n$ ungerade wird von ganzzahliger Division ausgegangen. Da für das Löschen oder Einfügen eines Elementes jedoch das Feld neu sortiert werden muss, d.h. die Zahl der Vertauschungen linear ist (Laufzeit in $\mathcal O(n)$), ist auch die Binäre Suche noch nicht optimal.

Interpolationssuche

Die Interpolationssuche stellt eine Verbesserung der Binären Suche dar, die Laufzeit im Mittel ist bedeutend besser. Das Verfahren beruht darauf, den Suchbereich besser einzugrenzen als nur durch einfache Halbierung. Anwendbar ist die Interpolationssuche allerdings nur auf einen Suchraum, bei dem der Feldindex proportional zum Suchschlüssel ist. Desweiteren müssen die Daten annähernd gleichverteilt sein. Betrachtet werden direkt die Schlüsselwerte und es wird ein Abstand geschätzt, der zum gesuchten Suchschlüssel führt. Der nächste zu überprüfende Feldindex wird aus einem Faktor und dem Suchschlüssel gebildet. Die Formel für den nächsten zu überprüfenden Wert lautet \begin{equation} x=uG+(s-S[uG])\cdot (oG-uG) / (S[oG]-S[uG]) \end{equation} wobei $x$ dem nächsten Suchindex, $s$ dem Suchschlüssel, $S$ dem Suchraum, $uG$ der unteren Intervallgrenze und $oG$ der oberen Intervallgrenze entspricht. Bei der Binären Suche besteht der Faktor anstatt einer Schätzung lediglich aus dem Wert $\frac{1}{2}$. Die Laufzeit der Interpolationssuche ist von der Eingabeverteilung stark abhängig, sind die Daten ungleichmäßig verteilt entsteht der Worst-Case mit einer Laufzeit in $\mathcal O(n)$. Desweiteren kann es für kleine $n$ sinnvoll sein, bei der Binären Suche zu bleiben, da der Rechenaufwand für die Interpolation zu einem zu geringen Vorteil in der Laufzeit führen würde. Bei sehr großen $n$ und nach den erläuterten Eigenschaften formatierten Daten liegt die Laufzeit allerdings in $\mathcal O(\lg \lg n)$. Der Beweis für diese Laufzeit wird an dieser Stelle nicht gebracht, da er den Rahmen der Veranstaltung erheblich sprengen würde.


Ein Beispiel für die Anwendung der Interpolationssuche:
Sei jedem $i$-ten Buchstabe des Alphabets die Zahl $i$ zugeordnet. (A und 1, B und 2 etc.)
Der Suchraum ist S=(A,A,A,C,E,E,E,G,H,I,L,L,M,N,P,R,S,X).
Gesucht wird der Buchstabe M.
Zur Umsetzung in Programmiersprachen mit zerobased-Arrays beginnt die untere Grenze bei 0.
Die zu vergleichenden Positionen wären \begin{equation} %x= 1 + (13-1) \cdot (17-1) / (24-1) = 9,3 = 9 x = 0 + (13-1) \cdot (17-0) / (24-1) = 8,35 = 8 \end{equation} Da der Wert an der Stelle 8 kleiner ist als der gesuchte Wert wird die Suche rechts der Mitte fortgesetzt (Addition mit 1). \begin{equation} %x= 9 + (13-9) \cdot (17-9) / (24-8) = 11 x = 9 + (13-9) \cdot (17-9) / (24-9) = 11,13 = 11 \end{equation} s. oben \begin{equation} %x= 11 + (13-11) \cdot (17-11) / (24-12) = 12 x = 12 + (13-13) \cdot (17-11) / (24-12) = 12 \end{equation} An der Stelle 12 steht das M, die Suche endet erfolgreich. 

Übung:
Wie viele Schritte wären mit der Binären Suche nötig gewesen?

Fibonacci Suche

Dieses Verfahren stellt eine Variation der Binären Suche da und arbeitet nach einer ähnlichen Vorgehensweise. Da die Laufzeit aber nicht besser ist wird es nur in Grundzügen dargestellt. Der Suchraum wird dabei nicht symetrisch geteilt, sondern asymetrisch. Da die Teilbereiche den Suchraum überdecken müssen, muss zumindest der zweite Teil des Suchbereiches berechnet werden. Dies geschieht durch Subtraktion, es ist keine Division mehr notwendig. Die Bildung der Teilbereiche geschieht dabei ebenso wie bei der Binären Suche solange, bis das Element bei der Teilung gefunden wurde beziehungsweise nur noch ein Element in einem Teilbereich vorhanden ist. Durch die Berechnung der Fibonacci-Zahlen wird der Algorithmus nicht nur komplizierter (Stichwort kognitive Effizienz), sondern die Berechnung fließt auch in die Laufzeit mit ein. Der Best-Case ist wie beim Binären Suchen in $\mathcal O(1)$, der Average-Case ergibt sich aus der Berechnung der Fibonacci-Zahlen $\mathcal O(\log_{1.618}(n+1))=O(\log_2 n)$.

Binäre Suchbäume

Die genutzte Datenstruktur wird nun vom Feld in einen Baum geändert. In den Knoten des Baumes werden die Datensätze beziehungsweise die Suchschlüssel abgespeichert. Damit ein Binärbaum ein binärer Suchbaum ist, muss jeder seiner Knoten die Suchbaum-Eigenschaft erfüllen. Diese besagt, dass der Suchschlüssel eines jeden Knotens im linken Teilbaum des betrachteten Knotens kleiner sein muss als der Suchschlüssel des betrachteten Knotens. Ebenso ist der Suchschlüssel des betrachteten Knotens kleiner als alle Suchschlüssel der Knoten im rechten Teilbaum. Die folgenden Abbildungen veranschaulichen die Suchbaum-Eigenschaft.
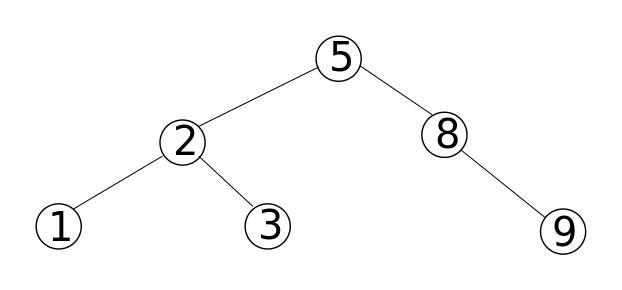
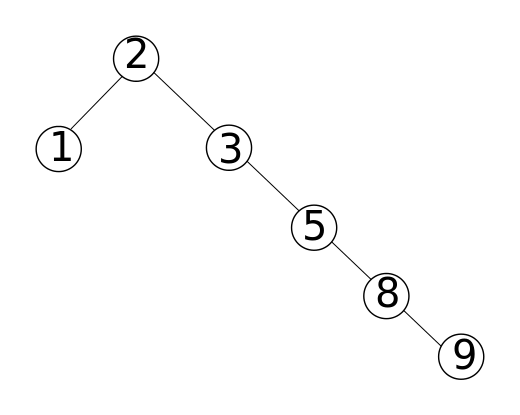
S3rostri Baum.png S3rostri Baum2.png
Ebenfalls wird deutlich, dass eine Reihe von Werten durch mehrere binäre Suchbäume dargestellt werden können, der Unterschied liegt in der Höhe $h$ der Bäume. Ein binärer Suchbaum kann als verkettete Liste implementiert werden, wobei jeder Knoten Verweise auf andere Knoten als Attribute erhält. Nötig sind die Verweise auf die zwei direkten Kinder sowie den Vaterknoten oder Parentnode. Gibt es keinen Kind- oder Vaterknoten, erhält das zugehörige Attribut den Wert NIL. Die Wurzel eines Binärbaumes ist also der Knoten, bei dem das Attribut Vaterknoten den Wert NIL besitzt. Die Laufzeit aller Operationen auf dem Baum ist immer abhängig von seiner Höhe. Für die Suche eines Elements benötigt man maximal $\mathcal O(h)$ Schritte. Besonders gut deutlich wird dies bei der Suche nach dem Maximum oder dem Minimum: Es wird immer am linken Teilbaum entlanggegangen, die Höhe $h$ legt die Schritte fest. Auch Operationen wie das Einfügen oder das Löschen von Datensätzen findet in Abhängigkeit der Baumhöhe statt. Interessant zu wissen wäre natürlich die Abhängigkeit der Laufzeit von $n$. Dies ist aber schwierig zu sagen, da, wie bereits erwähnt, verschiedene Bäume für die gleiche Eingabe möglich sind. So kann im Worst-Case (Baum erstellt nach sortierter Eingabe beginnend beim kleinsten Element) die Laufzeit durchaus in $\mathcal O(n)$ liegen (degenerierter Baum). Ziel muss es also sein, möglichst ausbalancierte Bäume zu bekommen. Diese werden in den folgenden Abschnitten vorgestellt.

Rot-Schwarz-Bäume

Um den Worst-Case der Binärbäume zu verhinden, entwickelte R. Bayer 1972 die Rot-Schwarz-Bäume. Jeder Knoten besitzt dabei ein zusätzliches Attribut (Bit), durch das seine Farbe beschrieben wird. Diese kann Rot oder Schwarz sein. Die näherungsweise Ausbalancierung wird nun dadurch erreicht, dass ein Pfad von der Wurzel bis zu einem Blatt nur eine festgelegte Färbung besitzen darf. Damit ein Binärbaum ein Rot-Schwarz-Baum ist, muss er folgende Eigenschaften erfüllen.

  1. Jeder Knoten ist entweder rot oder schwarz
  2. Die Wurzel und jedes Blatt sind schwarz
  3. Ist ein Knoten rot, sind seine beiden Kinder schwarz
  4. Für jeden Knoten $k$ gilt: Alle Pfade, die an $k$ starten und in einem Blatt des Teilbaums von $k$ enden, besitzen die gleiche Anzahl schwarzer Knoten


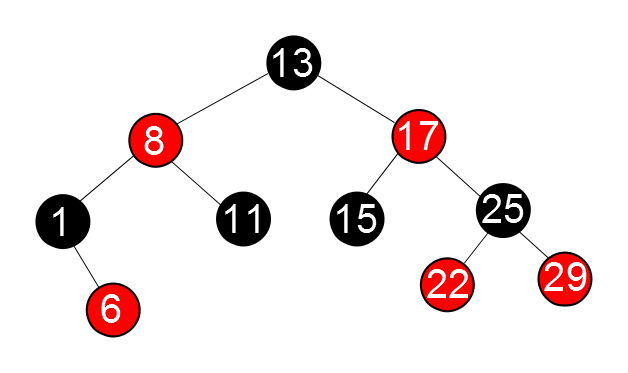
Baumsr.png
Entlang des Pfades von einem Knoten $x$ zu einem Blatt bezeichnet man die Anzahl der schwarzen Knoten als die Schwarzhöhe $bh(x)$. $x$ wird dabei nicht mitgezählt. Die Schwarzhöhe eines ganzen Baumes bezeichnet man als Schwarzhöhe seiner Wurzel. Desweiteren werden Blätter in den Betrachtungen weggelassen, da nur die inneren Knoten die Suchschlüssel enthalten. 

Lemma:
Die maximale Höhe für einen Rot-Schwarz-Baum mit $n$ Knoten beträgt $2\cdot \lg(n+1)$

Da die Laufzeiten der Operationen auf einem Binärbaum von dessen Höhe abhängen und nun bei den Rot-Schwarz-Bäumen die Höhe maximal $2 \cdot \lg(n+1)$ beträgt, können die Operationen in $\mathcal O(\lg n)$ durchgeführt werden, was eine enorme Effizienzsteigerung darstellt. Es sei darauf hingewiesen, dass bei bestimmten Operationen, wie dem Hinzufügen oder Löschen von Elementen, auf den Erhalt der Rot-Schwarz-Baum-Eigenschaften geachtet werden muss. Dies muss in den Verfahren ebenfalls erfolgen, doch kann gezeigt werden, dass auch diese Verfahren Laufzeiten in $\mathcal O(\lg n)$ haben. Vorausgesetzt wird dabei jedoch, dass die Daten im Arbeitsspeicher vorliegen. Bei sehr großen Datenmengen (Datenbanken) ist das nicht der Fall. Deshalb entwickelte R. Bayer 1972 den B-Baum, bei welchem ein Knoten tausende Kinder haben kann.

AVL-Bäume

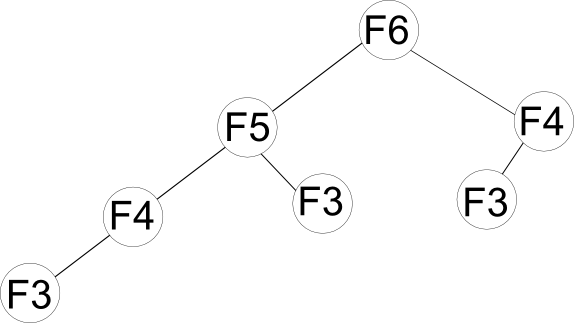
Wie bereits deutlich wurde ist es für Binärbäume wichtig, eine möglichst geringe Höhe zu haben. 1962 wurden von G. Adelson-Velskii und Y. Landis die AVL-Bäume eingeführt. Ein Binärer Suchbaum ist genau dann ein AVL-Baum, wenn jeder seiner Knoten höhenbalanciert ist. Ein Knoten ist genau dann höhenbalanciert, wenn sich die Höhen der Teilbäume der Kinder des Knotens maximal um eins unterscheiden. Der linke der obigen Binärbäume ist ein AVL-Baum, der rechte nicht. Desweiteren sind AVL-Bäume besser balanciert als Rot-Schwarz-Bäume, da es für jeden AVL-Baum möglich ist, einen Rot-Schwarz-Baum anzugeben. Andererseits gibt es Rot-Schwarzbäume, die keine AVL-Bäume sind. Beweis:
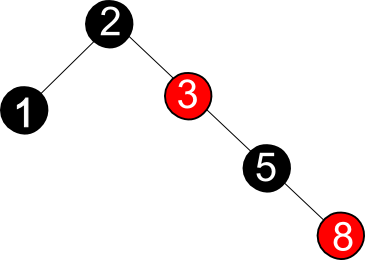
S3rostri sr-noavlbaum.png

Dieser Baum ist eine Variation des rechten Baumes der Abbildung aus Binärbäume. Er ist zwar ein Rot-Schwarz-Baum, aber kein AVL-Baum. Da wie üblich bei Binärbäumen die Laufzeit abhängig von der Höhe ist, liegt das größte Interesse im Verhältnis von $n$ zur Höhe $h$. 

Die Laufzeit der Suche in einem AVL-Baum liegt in $\mathcal O(\log n)$

Dafür ist zu zeigen, dass die Höhe $h$ eines AVL-Baumes mit $n$ Knoten $\log n$ beträgt.

Damit ist gezeigt, dass die Höhe eines AVL-Baumes mit $n$ Knoten $\log n$ beträgt. Die Unterschiede zwischen Rot-Schwarz-Bäumen und AVL-Bäumen sind gering, aber vorhanden. In empirischen Analysen haben sich die AVL-Bäume jedoch als besser herausgestellt, sodass sie die empfohlene Datenstruktur darstellen.

Hashing

Das häufig genutzte Hashing wird vor allem dort angewandt, wo große Datenmengen in kurzer Zeit durchsucht werden müssen. Man benötigt für das Hashing eine sogenannte Hashtabelle und eine Hashfunktion $h$. Diese berechnet als erstes eine natürliche Zahl aus dem Schlüssel $k$. Der zweite Schritt besteht in der Berechnung beziehungsweise Transformation dieser Zahl auf eine Position der Hashtabelle. Häufig werden diese beiden Teilschritte zusammengefasst und allgemein als Funktion der Hashfunktion bezeichnet. Die Hashtabelle $t$ wird meist als einfaches Feld mit der Länge $m$ implementiert. Allerdings sagt die Feldgröße nichts über deren Belegung aus. Dazu bedarf es der Variablen $n$, welche angibt, wie viele Datensätze wirklich im Feld gespeichert sind. Aus $m$ und $n$ lässt sich nun der Belegungsfaktor $\alpha =\frac{n}{m}$ berechnen. Hashfunktionen können zwar surjektiv sein, niemals aber injektiv. Deshalb ist es möglich, dass zwei Schlüsseln der gleiche Hashwert zugeordnet wird, es gilt also $h(k)=h(k')$. Dies bezeichnet man als Kollision, $k'$ nennt man Überläufer. Diese Kollisionen sind nicht selten, im Gegenteil. Man muss davon ausgehen, dass es zu Kollisionen kommt. Ein Vergleich ist mit dem Geburtstagsparadoxon möglich, dem die gleiche Berechnung zugrunde liegt. Angewandt bedeutet dies, dass bei einer Hashtabelle mit $m=365$ und $n=23$ die Wahrscheinlichkeit für eine Kollision größer als $0.5$ ist. Für weitere Betrachtungen zur Auftretungswahrscheinlichkeit von Kollisionen siehe V. Heun: Grundlegende Algorithmen. Natürlich gibt es viele verschiedene Hashfunktionen mit unterschiedlichen Berechnungsansätzen und Kollisionswahrscheinlichkeiten. Gemeinsam ist ihnen, dass sie schnell zu berechnen sein müssen, das heißt ihre Laufzeit darf nicht von der Anzahl der Schlüssel abhängig sein, sondern nur vom Schlüsselwert. Einige seien im Folgenden vorgestellt.


Berechnung des Hashcodes einer Zeichenkette

Häufig sind die Schlüsselwerte Zeichenketten, aus denen die Hashfunktion Zahlenwerte berechnen muss. Deshalb soll hier ein Beispiel für eine solche Berechnung gezeigt werden. Diese dient als Vorbedingung für die unten aufgeführten Methoden zur Berechnung der Position in einer Hashtabelle. Die Funktion zur Erzeugung des Hashcodes einer Zeichenkette wurde in Java als anwendbare Methode auf ein Datum des Typs String implementiert (Methode in Klasse java.lang.String). Die Grundidee bestand in der einfachen Aufsummierung der Zeichencodes, ähnlich einer Summe von Zahlen. Diese Methode ist allerdings nur für längere Zeichenketten praktikabel und die Streuung ist nicht sehr hoch. Deshalb wurde dieses Verfahren um einen Faktor erweitert. \begin{equation} zahl= ((int)\downarrow k[1]) \cdot 31^{x-1} + ((int)\downarrow k[2]) \cdot 31^{x-2} + \dots + ((int)\downarrow k[x]) \end{equation} $x$ entspricht dabei der Länge der Zeichenkette $k$. Der Zahlenwert zu jedem Buchstabe ist der Wert im ASCII-Code.

Es kann durchaus vorkommen, dass es einen Überlauf des Datentypes integer bei der Berechnung der Potenzen gibt. Doch spielt das keine Rolle, da keine mathematische Exaktheit des Ergebnisses gefordert ist und das Ergebnis für den Zweck des Hashings gut geeignet ist (Quelle: "Algorithmen und Datenstrukturen" von Pomberger und Dobler, Seite 286). 

Übung:
Berechnen Sie den Hashcode für die Zeichenkette "AuK".

Dieses Ergebnis stimmt mit dem Resultat der Java-Methode java.lang.String.hashCode() überein. Die Berechnung lässt sich allerdings deutlich durch das Horner-Schema vereinfachen.

Dieses Schema, angewandt auf das Polynom zur Berechnung des Hashcodes eines Strings, führt zur nachfolgenden Implementation der Funktion in Java.

Mit Hilfe der so berechneten Werte lässt sich die zweite Teiloperation einer Hashfunktion, die Bestimmung der Position in der Hashtabelle, durchführen.

Divisionsmethode

Die Divisionsmethode ist leicht zu implementieren, ihr liegt lediglich die Gleichung \begin{equation} h(k) = k \bmod m \end{equation} zugrunde, wobei $k$ der Suchschlüssel beziehungsweise der vorher berechnete numerische Wert ist. Gute Ergebnisse bringt dieses Verfahren nur, wenn für $m$ eine Primzahl gewählt wird, welche möglichst weit von einer Zweierpotenz entfernt ist. Die Berechnung geht sehr schnell, die Streuung der Methode ist allerdings generell ungünstig.

Multiplikationsmethode

Diese Methode ist deutlich besser geeignet als die Divisionsmethode, da die Wahl des Parameters $m$ keine gravierenden Auswirkungen auf die Ergebnisse der Hashfunktionen hat. \begin{equation} h(k) = \lfloor(k\cdot a - \lfloor k\cdot a\rfloor) \cdot m\rfloor \end{equation} Zuerst wird der Schlüssel mit einer Zahl $a$ zwischen null und eins multipliziert (optimale Wahl ist $a=0,6180$, siehe D. E. Knuth Band 3 The Art of Computer Programming). Davon wird nur der gebrochene Teil verwendet und mit $m$ multipliziert. Das Ergebnis hiervon wird abgerundet und stellt das Endergebnis dar.

Kollisionsbehandlung

Wie bereits weiter oben erläutert wird, kommt es definitiv zu Kollisionen (außer bei Perfektem Hashing, was jedoch voraussetzt, das man alle Elemente kennt und die Anzahl der Suchschlüssel klein ist). Es gibt verschiedene Methoden, wie mit diesen Kollisionen umgegangen wird. Vorgestellt werden soll die Kollisionsauflösung durch Verkettung sowie die Kollisionsbehandlung durch offene Adressierung. Die Elemente, die durch die Hashfunktion einem Platz in der Hashtabelle zugewiesen werden, werden bei der Verkettung auch dort gespeichert. Dazu besteht jedes Feldelement nicht aus lediglich einem Speicherplatz, sondern einer verketteten Liste. Die Tabelle enthält dann nur einen Verweis auf diese Liste. Soll ein bestimmtes Element gesucht werden, wird zuerst die Hashtabelle ausgewertet und danach die Liste linear durchsucht. Die Laufzeit für die Suchoperation in solch einer Tabelle ist abhängig von dem bereits eingeführten Belegungsfaktor $\alpha$. Der Worst-Case ist leicht zu finden: Alle Elemente werden an die selbe Position der Hashtabelle geschrieben, das heißt sie haben den gleichen Hashwert. Es entsteht also eine Liste der Länge $n$, die Laufzeit liegt in $\mathcal O(n)$. Eine Lösung dieses Problems besteht in der Verwendung einer zufällig gewählten Hashfunktion aus einer Menge von Hashfunktionen. Dies bezeichnet man als Universelles Hashing, was aber im Folgenden nicht betrachtet wird. Die mittlere Laufzeit der Suche in einer Hashtabelle liegt in $\mathcal O(1+\alpha)$. Auf den Beweis wird nicht im Detail eingegangen, da es einen Vortrag über Hashing im Detail gibt, der dies sicher behandelt. Eine Doppelung des Inhaltes erscheint nicht sinnvoll.

String-Matching

Auch dieses Thema gehört zu dem Abschnitt "Suchen" und soll deshalb nicht unerwähnt bleiben. Da es jedoch einen einzelnen Vortrag gibt, der sich ausschließlich mit dieser Thematik befasst und diese viel detaillierter darstellen kann, wird das String-Matching hier nicht behandelt.

Übungen

Uebung.pdf (0.1 MB)

Literaturverzeichnis

Kontakt

Sollten während der Nacharbeitung der Vorlesung Fragen auftreten, können diese gern gestellt werden.

Dana Müller
Robert Stricker
Von „https://programmingwiki.de/AuK/Sortieren_und_Suchen_WS13-14“
Persönliche Werkzeuge