Sortieren und Suchen SS12
Aus ProgrammingWiki

Inhaltsverzeichnis
|
Ordnungskriterium
Das Ordnungskriterium in einer Datensammlung bezieht sich nur auf wenige Elemente eines Datensatzes. Dies kann im Beispiel eines Telefonbuches eine lexikographische Anordnung der Namen sein. Die Suche in der Datensammlung orientiert sich an dem Ordnungskriterium.
Datensatz hat den Aufbau: Schlüssel - Inhalt
Sortieren von Zahlen
Eine Eingabefolge von $n$ Zahlen $(a_1,a_2, … ,a_n)$ wird durch Umordnung in eine Ausgabefolge umgewandelt, für die gilt $(a_1 < a_2 … < a_n)$.
Einteilung von Sortierverfahren und Begriffsklärungen
- in-place-Sortierverfahren
- Sortierung erfolgt innerhalb des Eingabefeldes
- out-of-place-Sortierverfahren
- Sortierung erfolgt außerhalb des Eingabefeldes
- Interne Sortierverfahren
- Zu sortierende Elemente befinden sich im Hauptspeicher
- Externe Sortierverfahren
- Zu sortierende Elemente befinden sich auf der externem Speichermedium
- stabile Sortierverfahren
- Reihenfolge identischer Elemente bleibt nach Sortierung erhalten
- instabile Sortierverfahren
- Reihenfolge der Datensätze mit gleichem Sortierschlüssel bleibt nicht erhalten
Effizienz
- geringer Speicherplatzverbrauch
- geringe Laufzeit
Bei der Ermittlung einer aussagekräftigen Laufzeit treten folgende Probleme auf:
- Eigenschaften der Maschine auf der Algorithmus ausgeführt wird
- Qualität der Implementierung des Algorithmus
- Instanz der Problemklasse
- Größe der Eingabe
Die exakte chronometrische Arbeitszeit eines Algorithmus ist uninteressant. Es braucht eine Angabe, die weitgehend unabhängig von speziellen Ausprägungen der vorangegangenen Einflüsse ist.
Fallunterscheidungen
Um den Einfluss der Instanz der Problemklasse in eine praxistaugliche Aussage über die Laufzeit münden zu lassen, ist es erforderlich Fallunterscheidungen vorzunehmen.
Best case
Das Problem tritt in seiner geringsten Ausprägung auf und fordert die kürzeste Laufzeit und den wenigsten Speicherplatz.
Worst case
Das Problem tritt in seiner größten Ausprägung auf und fordert die längste Laufzeit und den meisten Speicherplatz.
Average case
Der durchschnittliche Fall ist schwer zu definieren.
Welcher Fall liefert eine praxistaugliche Aussage? Der best case scheidet aus. Die Aussage, dass die Laufzeit eines Algorithmus nicht besser als eine bestimmte Größe sein wird, ist von geringem Interesse. Der average case und der worst case sind aussagekräftiger und maßgeblicher für die Entscheidung über die Verwendung eines Algorithmus. Der worst case ist eine Garantie dafür, dass egal welche Instanz eines Problems auch immer auftreten mag, die Laufzeit niemals schlechter wird als im worst case. Er ist die obere Schranke für die Laufzeit. In Abhängigkeit mit welcher Häufigkeit der worst case in der Praxis auftritt, ist der average case von größerer Bedeutung. So hat Quicksort im ungünstigsten Fall eine Laufzeit von $\mathcal{O}(n^2)$, findet aber durch sein günstiges Laufzeitverhalten im mittleren Fall häufig Anwendung.
Selection Sort (Auswahlsortieren)
Selection Sort ist ein instabiles in-place-Sortierverfahren. Die zu sortierenden Elemente werden in einen sortierten und einen unsortierten Bereich aufgeteilt.
Das Verfahren
- Ermittlung des kleinsten Elementes des unsortierten Feldes
- Tausch mit dem ersten Element des unsortierten Feldes
- mit zweitem Element und Rest des unsortierten Teilfeldes ebenso verfahren
Laufzeitverhalten
Bei einigen Sortierverfahren ist die Anzahl der notwendigen Sortierschritte abhängig von einem Schlüsselelement, welches als Vergleichswert dient. Anhand des Schlüssels wird mittels Vergleichsoperatoren die Position jedes Elementes im sortierten Feld bestimmt. Die Anzahl der Schritte bis zum sortierten Ergebnis, hängt bei Selection Sort nicht von der Auswahl eines Sortierschlüssels ab, sondern ist abhängig von der Elementanzahl. Somit existiert kein worst case oder best case. Zur Analyse des Laufzeitverhaltens genügt daher eine Grobanalyse.
- $(n – 1)$ Schlüsselvergleiche im ersten Durchlauf
- $(n – 2)$ Vergleiche im zweiten Durchlauf…
- $T(n)=(n–1)+(n–2)+…+2+1$
- $T(n)=n \cdot \frac{n–1}{2}$
- $T(n)=\frac{n^2}{2}–\frac{n}{2}$
Das Verfahren hat im Hinblick auf die Anzahl der nötigen Schlüsselvergleiche eine Laufzeit von $\mathcal{O}(n^2)$
Die Elemente sind $(n–1)$ mal zu vertauschen bis das Array sortiert vorliegt. Daraus ergibt sich eine Ordnung von $n$.
Begründet durch die asymptotische Laufzeitkomplexität von $\mathcal{O}(n^2)$ ist Selection Sort ein für große $n$ ungünstiges Sortierverfahren.
Da es sich bei Selection Sort um ein in-place Verfahren handelt, wird nur für das unmittelbare Vertauschen von zwei Elementen zusätzlicher Speicherplatz benötigt. Soll beispielsweise das Element X und das Element Y vertauscht werden, bedarf es eines zusätzlichen Speicherplatzes Z, der den Wert von X aufnimmt. Nun kann der Wert von Y auf X geschrieben werden und im Anschluss Z auf Y.
Insertion Sort
Das Verfahren
- Unterteilung des unsortierten Feldes in sortierten und unsortierten Bereich
- erstes Element $a_1$ wird als sortiert angesehen
- Schlüsselelement wird festgelegt
- Verschiebung der sortierten Elemente, die größer als Schlüsselelement sind, um jeweils eine Stelle nach rechts
- Einfügen des Schlüsselelementes in entstandene Lücke
Laufzeitverhalten
Die Laufzeit von Insertion Sort ist von der Anzahl der Schleifendurchläufe und von der Anzahl der im Schleifenkörper befindlichen Basisoperationen abhängig. Im Allgemeinen ergibt sich die Laufzeit aus der Summe der Produkte von Kosten und Anzahl der ausgeführten Basisoperationen. Unter Kosten versteht man die chronometrische Arbeitszeit zur Ausführung von Basisoperationen oder Auswertung von Bedingungen im Schleifenkopf. Dies stellt sich im Allgemeinen folgendermaßen dar.
| Zeile | Kosten | Zeit |
|---|---|---|
| for j = 2 to Länge[A] | $c_1$ | $n$ |
| key = A[j] | $c_2$ | $n-1$ |
| i = j-1 | $c_3$ | $n-1$ |
| while i > 0 and A[i] > key | $c_4$ | $\sum\nolimits_{j=2}^n t_j$ |
| do A[i+1] = A[i] | $c_5$ | $\sum\nolimits_{j=2}^n (t_j-1)$ |
| i = i-1 | $c_6$ | $\sum\nolimits_{j=2}^n (t_j-1)$ |
| A[i+1] = key | $c_7$ | $n-1$ |
Rechung: $T(n)=c_1 \cdot n+c_2 \cdot (n-1)+c_3 \cdot (n-1)+c_4 \cdot \sum\limits_{j=2}^n t_j+c_5 \cdot \sum\limits_{j=2}^n (t_j-1)+c_6 \cdot \sum\limits_{j=2}^n (t_j-1)+c_7 \cdot (n-1)$
Weiterhin ergeben sich bei Insertion Sort, durch die verschieden Instanzen einer Problemklasse, unterschiedliche Laufzeiten.
Best case
- alle Elemente des Eingabearrays sind bereits sortiert
- keine Operationen zur Schaffung einer Ordnung erforderlich
$T(n)=c_1 \cdot n + c_2 \cdot (n-1) + c_3 \cdot (n-1)+ c_4 \cdot (n-1) + c_7 \cdot (n-1)$
$T(n)=(c_1+c_2+c_3+c_4+c_7) \cdot n - (c_2+c_3+c_4+c_7)$
$T(n) = a \cdot n+b = \mathcal{O}(n)$
Worst Case
- alle Elemente sind absteigend sortiert
- Platz zum einfügen wird erst am Anfang des sortierten Teils gefunden
- $n \cdot \frac{n + 1}{2}$ Schritte
$ \sum\limits_{j=2}^{n} j=\frac{n \cdot (n+1)}{2}-1$
und
$ \sum\limits_{j=2}^{n} (j-1)=\frac{n \cdot (n-1)}{2}$
$T(n)=c_1 \cdot n+c_2 \cdot (n-1) + c_3 \cdot (n-1) + c_4 \cdot (\frac {n \cdot (n+1)}{2}-1)+c_5 \cdot (\frac {n \cdot (n-1)}{2})+c_6(\frac {n \cdot (n-1)}{2})+c_7 \cdot (n-1) $
$T(n)=(\frac{c_4}{2}+\frac{c_5}{2}+\frac{c_6}{2}) \cdot n^2 +(c_1+c_2+c_3+\frac{c_4}{2}-\frac{c_5}{2}-\frac{c_6}{2}+c_7) \cdot n-(c_2+c_3+c_4+c_7)$
$T(n)=a \cdot n^2 + b \cdot n + c = \mathcal{O}(n^2)$
Average case
Die Entscheidung, wie die durchschnittliche Eingabe eines Problems aussieht, ist schwer. Für Insertion Sort nehmen wir daher an, dass die Hälfte der Elemente im Teilarray A[1…j-1] kleiner und die andere Hälfte der Elemente größer als das jeweilige Schlüsselelement A[j] sind. Für die Ermittlung der richtigen Einfügeposition im Teilarray A[1…j-1] ist daher von tj = j/2 auszugehen. Daraus ergibt sich eine Laufzeit von $\mathcal{O}(n^2)$.
Bei Insertion Sort handelt es sich um ein in-place-Verfahren. Es benötigt daher wenig zusätzlichen Speicher. Aufgrund einer durchschnittlichen Laufzeit von $\mathcal{O}(n^2)$ ist es nur für kleine $n$ geeignet.
$T(n)=c_1\cdot n+(c_2+c_3+c_7)\cdot (n-1)+c_4 \cdot \sum\limits_{j=2}^n \frac{j}{2} + (c_5+c_6)\cdot \sum\limits_{j=2}^n (\frac{j}{2}-1)$
$T(n)=( \frac{c_4+c_5+c_6}{4} )\cdot n^2 + (c_1+c_2+c_3+c_7+\frac{c_4-3\cdot c_5-3 \cdot c_6}{4})\cdot n-c_2-c_3-c_7+\frac{c_5+c_6-c_4}{2}$
$T(n)=a\cdot n^2 + b\cdot n+c = \mathcal{O}(n^2)$
Mergesort (sortieren durch zusammenführen)
Divide and Conquer
Ist ein Problem zu groß, um es direkt lösen zu können, zerlege es in beherrschbare Instanzen des selben Problems und löse diese. Die Teillösungen werden abschließend zur Gesamtlösung zusammengefügt. Das ist das Prinzip von „Teile und Herrsche“. Mergesort arbeitet nicht in-place und ist ein stabiles Verfahren. Es eignet sich besonders zum sortieren von Daten auf Sekundärspeichern (externes Sortieren).
Das Verfahren
- Teilung der Folge A in zwei Teilfolgen A1 und A2 jeweils der Länge $\frac{n}{2}$
- rekursive Zerlegung des Eingabefeldes in Teilfelder, bis Wert in jedem Feld atomar vorliegt (die Länge 1 hat)
- Zusammenführung der Teilfelder bei gleichzeitiger Sortierung
- Zusammenführung der sortierten Teilfelder im Reißverschlussverfahren zum Gesamtergebnis
Laufzeitverhalten
Mergesort hat einen höheren Speicherplatzbedarf als beispielsweise Selection Sort. Dies ist durch die Verwendung von Hilfs-Arrays bedingt, welche für die Teilung des Eingabearrays erforderlich sind.
Ist $T(n)$ die Zeit zur Lösung eines Problems und $n$ die Eingabegröße, so kann das Problem für den Elementarfall (Eingabe besteht nur aus einem Element) $n \le c$ für eine Konstante $c$ in konstanter Zeit gelöst werden. Es ergibt sich daraus eine Laufzeit von $\mathcal{O}=(1)$. In diesem Fall gehen wir davon aus, dass die Aufteilung des Eingabearrays zu $a$ Teilproblemen mit der Länge $\frac{1}{b}$ führt. Ist $D(n)$ die Zeit um das Problem zu zerlegen und $C(n)$ die Zeit um die Teilprobleme zur Gesamtlösung zu vereinigen, ergibt sich die folgende Rekursionsgleichung.
$T(n) = \begin{cases} \mathcal{O}(1), & \text{wenn } n \le \text{c}\\ a \cdot T(\frac{n}{b}) + D(n) + C(n), & \text{sonst }\\ \end{cases}$
Der Aufwand zur Aufteilung des Eingabearrays ist immer gleich und nicht von der Eingabegröße abhängig, somit ist $D(n) = O(1)$. Ist der gesamte Zeitaufwand zur Herstellung einer Ordnung in der gesamten Eingabe gleich $T(n)$, dann beträgt er für zwei Teilfolgen der Länge $\frac{n}{2}$ der Eingabe gleich $2T\frac{n}{2}$. Diesen Beitrag leistet die Sortierung der Teilfolgen zur gesamten Laufzeit. Das Zusammenführen der sortierten Teilfolgen zur Gesamtlösung hat einen zeitlichen Aufwand, der in Abhängigkeit von der Eingabegröße steht. Er trägt für
$C(n) = O(n)$ zur gesamten Laufzeit bei. Addiert man die einzelnen Beiträge zusammen, so ergibt sich für den schlechtesten Fall die folgende Rekursionsgleichung.
$T(n) =
\begin{cases}
\mathcal{O}(1), & \text{wenn } n \text{ = 1}\\
2 \cdot T\frac{n}{2} + \mathcal{O}(n), & \text{wenn } n \text { > 1}\\
\end{cases}$
Zur Beantwortung der Frage nach der Laufzeit für den schlechtesten Fall, ziehen wir das Mastertheorem heran. Diese Methode unterscheidet drei Fälle zur Bestimmung der Laufzeit, beim Vorliegen von Rekursionsgleichungen. Sie muss der folgenden Form entsprechen.
$T(n) = a \cdot T\frac{n}{b} + f(n)$
$f(n)$ ergibt sich aus der Summe von $D(n)$ und $C(n)$. Bei Merge Sort findet der zweite Fall des Mastertheorems Anwendung, da sich für $f(n) = n^{log_ba}$ aus $f(n) = n^{log_22}$ gleich $f(n) = \mathcal{O}(n)$ ergibt. Die Laufzeit ergibt sich somit aus $T(n) = n^{log_22} \cdot log(n)$ und ist von der Ordnung $n \cdot log(n)$.
Quicksort
Quicksort ist ein auf das divide and conquer Prinzip basierendes Sortierverfahren, unterscheidet sich aber bezüglich seiner Arbeitsweise von Mergesort. Es arbeitet in-place und benötigt nur zum Vertauschen zweier Elemente zusätzlichen Speicherplatz.
Das Verfahren
- beliebiges Pivot-Element X (Schlüssel) aus unsortiertem Array wählen
- durchsuchen des Array, beginnend von links, nach Element größer X
- durchsuchen des Array, beginnend von rechts, nach Element kleiner X
- vertauschen der beiden Elemente
- fortfahren bis man sich aus beiden Richtungen trifft
- Array ist nun in Elemente kleiner X und größer X zerlegt
- X befindet sich an richtiger Position
- rekursive Anwendung des Verfahrens auf alle entstehenden Teilarrays
Ein Zusammenführen der Teilarrays nach dem letzten Durchlauf ist nicht erforderlich, da nur im Eingabearray gearbeitet wurde und das Gesamtarray bereits im sortierten Endzustand vorliegt.
Laufzeitverhalten
Die Laufzeit von Quicksort hängt unter anderem von der Auswahl des Pivot-Elementes ab. Quicksort arbeitet besonders effizient, wenn Teilarrays gleicher Größe entstehen.
Best case
In diesem Fall wird das Pivot - Element bei jedem Durchlauf zufällig so gewählt, dass jeweils ein Teilarray der Größe $\frac{n}{2}$ und eines der Größe $\frac{n}{2} - 1$ durch den rekursiven Aufruf übergeben wird, sofern die Größe des Eingabearrays eine Zweierpotenz ist. Das Ergebnis eines jeden Zerlegeprozesses ist, dass sich jeweils das gewählte Schlüsselelement an der richtigen Position im Array befindet. Da dies für jedes Element im Eingabearray festzustellen ist, ergibt sich dafür eine Laufzeit von $\mathcal{O}(n)$. Dies kann in folgender Rekurrenzgleichung dargestellt werden.
$T(n) = 2T\frac{n}{2} + \mathcal{O}(n)$
Da die Form der Gleichung, der für die Anwendung des Mastertheorems entsprechenden Form genügt, kann dieses zur Lösung der Gleichung herangezogen werden. Daraus ergibt sich eine Laufzeit von $\mathcal{O} (n \cdot log (n))$.
Worst case
Im ungünstigsten Fall wird das Schlüsselelement bei jedem Durchlauf so gewählt, dass jeweils ein Teilarray mit nur einem Element und eines mit dem Rest der Eingabe entsteht. Dies ist der Fall, wenn eine Eingabe erfolgt, die bereits sortiert ist. Das Element, welches allein steht, ist das Schlüsselelement. Es befindet sich an der richtigen Stelle im Array und muss daher nicht Teil des rekursiven Aufrufs sein. Die Laufzeit ergibt sich in diesem Fall aus folgender Gleichung. Sie ist für den schlechtesten Fall von der Ordnung $n^2$.
$T(n) = T(n-1) + \mathcal{O}(n)$
Average case
Mit Hilfe eines Rekursionsbaumes lassen sich auch die entstehenden Kosten für eine unbalancierte Aufteilung des Eingabearrays sehr einfach ermitteln. Jede Ebene des Baumes erzeugt in Summe cn Kosten. Die Baumtiefe ergibt sich aus dem Logarithmus von $n$, zur Basis des Kehrwertes des größeren Anteils von $n$, in der zweiten Ebene des Baumes. Sie ist $log(n)$. Da $log(n)$ Ebenen zu je $cn$ Kosten vorhanden sind, ergibt sich daraus eine Laufzeit von $\mathcal{O}(n \cdot log(n))$. Im Mittel wechseln sich gute und schlechte Aufteilungen ab. Auch hier kann eine Laufzeit von $\mathcal{O}(n \cdot log(n))$ nachgewiesen werden. In der Praxis bewegt sich die Laufzeit näher am günstigsten Fall.
Randomized Quicksort
Eine günstige Lösungsstrategie ist es, zu versuchen den ungünstigsten Fall abzufangen. Dies gelingt durch das zufällige Auswählen des Schlüsselelementes aus dem Bereich A[1…n]. Es wird mit dem Element getauscht, welches sich unter dem Index des bisherigen Schlüsselelementes a1 befindet. Der ungünstigste Fall kann dadurch nicht vollkommen ausgeschlossen werden, aber die Wahrscheinlichkeit seines Auftretens ist deutlich reduziert
Heapsort
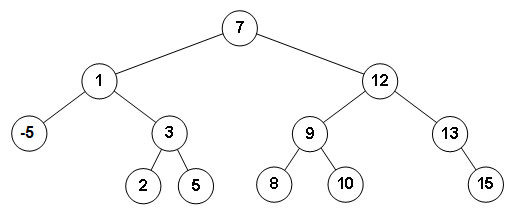
Zum Verständnis von Heapsort ist es wichtig die Datenstruktur Baum näher zu beleuchten, im Speziellen die des binären Baumes. Ein Baum besteht aus Knoten und Kanten. Von oben beginnend, wird der erste Knoten Wurzelknoten genannt. Die unmittelbar darunter liegenden Knoten sind seine Kindknoten. Im binären Baum kann jeder Elternknoten nur zwei Kindknoten besitzen. Knoten ohne Kindknoten werden Blätter genannt. Die Verbindungen zwischen den Knoten werden Kanten genannt. In dieser Struktur lassen sich Daten nach verschiedenen Ordnungsprinzipien unterbringen. In diesem Beispiel gehen wir wieder von Zahlenwerten aus, die untergebracht werden. Die Heapeigenschaft der Datenstruktur ist dann gegeben, wenn der Wert eines jeden Elternknoten immer größer ist als die Werte seiner Kindknoten. Nummeriert man die Knoten von oben beginnend und in jeder Ebene von links nach rechts durch, so lassen sich diese auch nachvollziehbar in einem Array unterbringen. Der Baum ist eine rekursive Datenstruktur, da er aus einem Wurzelknoten besteht, dessen Kindknoten wiederum Wurzelknoten von darunter liegenden Bäumen sein können. Diese rekursive Struktur bietet eine rekursive Herangehensweise beim Umgang mit den Datenobjekten geradezu an. Zur Herstellung der Heapeigenschaft im einem Baum, in dem diese nicht gegeben ist, ist es erforderlich die Elternknoten und deren Kindknoten von unten beginnend zu prüfen. Jeder Unterbaum enthält maximal drei Knoten, von denen der Knoten mit der größten Wertigkeit zum Wurzelknoten des Unterbaumes erhoben wird. Nach mehrfacher Ausführung dieser Prozedur, durch rekursive Aufrufe, ist die Heapeigenschaft hergestellt. Um nun eine sortierte Folge herzustellen, macht man sich das Ordnungsprinzip dieser Baumstruktur zu nutze. Das Wurzelelement, auf welches ohne Mühe zugegriffen werden kann, ist das Element mit der größten Wertigkeit im gesamten Baum. Dieses wird mit dem am weitesten rechts stehenden Blatt vertauscht. Dieses Blatt wird nun für den weiteren Prozess ausgeblendet. Da nun die Heapeigenschaft nicht mehr gegeben ist, ist diese wieder herzustellen. Nun befindet sich wieder das Element mit der größten Wertigkeit im Baum an der Position des Wurzelelementes, welches wieder mit dem am weitesten rechts befindlichen Blatt ausgetauscht wird und anschließend für den Folgeprozess versteckt wird. Dieser Vorgang wird solange fortgesetzt, bis eine Folge in aufsteigender Sortierung vorliegt.
Im Gegensatz zu Quicksort hat Heapsort auch im ungünstigsten Fall eine Laufzeit von $\mathcal{O}(n \cdot log( n))$. Dieser tritt ein, wenn das niederwertigste Element gleichzeitig das Wurzelelement ist. Um es im Baum an die richtige Position zu bringen, welche die eines Blattes ist, sind maximal so viele Schritte nötig, die der Anzahl der Ebenen des Baumes entsprechen. Ein binärer Baum mit $n$ Elementen kann höchstens aus $log(n)$ Ebenen bestehen. Somit kann man sagen, dass die Laufzeit zur Herstellung der Heapeigenschaft im schlechtesten Fall von der Ordnung $\mathcal{O}(h)$ oder $\mathcal{O}(log (n))$ ist. Um eine aufsteigende Sortierung herzustellen, werden die Blattobjekte und die Wurzelobjekte vertauscht. Dieser Vorgang findet $n$ mal statt. Im ungünstigsten Fall gelangt dadurch immer das niederwertigste Element nach oben. Somit kann von einer Laufzeit von $\mathcal{O}(n \cdot log( n))$ ausgegangen werden.
Untere Schranke für Sortierverfahren
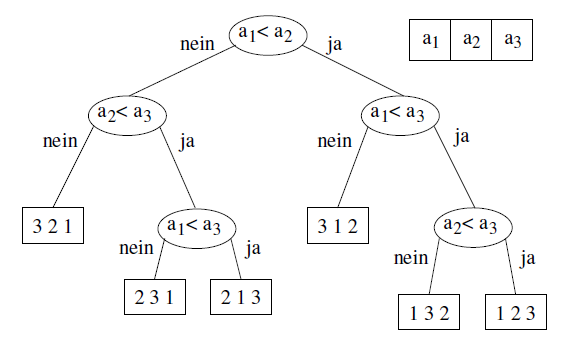
Die bisher betrachteten Sortierverfahren können mit einer Laufzeit aufwarten, die für den worst case im besten Fall von der Ordnung $\mathcal{O}(n \cdot log( n))$ ist. Die Frage die sich nun stellt, ist die nach der Unterschreitung dieser Marke. Gibt es Sortierverfahren die schneller sind als $\mathcal{O}(n \cdot log( n))$? Die vorangegangenen Verfahren beruhen auf Vergleichsoperationen ($\le >$). Zum besseren Verständnis lässt sich dieser Sachverhalt in einem Vergleichsbaum verdeutlichen.
In diesem Beispiel soll eine Eingabe von drei Elementen aufsteigend sortiert werden. Jeder Knoten des Baumes stellt eine Vergleichsoperation zwischen zwei Elementen dar. In Abhängigkeit wie der Vergleich ausfällt, wir entweder die rechte oder die linke Kante weiter verfolgt. Mit dem Erreichen eines Blattes sind alle nötigen Vergleiche durchgeführt, um eine Sortierung herzustellen. Das jeweilige Blatt gibt die richtige Anordnung der Eingabeelemente an. Jedes Sortierverfahren muss in der Lage sein, aus jeder möglichen Permutation eine gültige Ausgabe zu erzeugen. Demnach muss der Baum auch alle möglichen $n!$ Permutationen der Eingabeelemente als Blätter enthalten. Die Anzahl der nötigen Vergleiche entspricht dabei der Länge des Weges von der Wurzel bis zum Blatt, für eine Instanz des Problems. Die untere Schranke für die auszuführenden Vergleiche des Sortiervorgangs, entspricht demnach der größten Höhe des Baumes, unter der Vorraussetzung, dass alle $n!$ Permutationen untergebracht werden müssen. Ein Baum der Höhe $h$ kann maximal $2^h$ Blätter haben, also folgt daraus $n! \le 2^h$ oder $log(n!) \le h$. Mit der stirlingschen Formel kann man nachweisen, dass sich mit vergleichbasierten Algorithmen, für das Auftreten des worst case, eine Laufzeit erreichen lässt, die im günstigsten Fall $\mathcal{O}(n \cdot log( n))$ ist. Somit sind Heapsort und Mergesort asymptotisch optimale Verfahren.
Countingsort
Die Verwendung von Countingsort unterliegt bestimmten Bedingungen. Zum einen können nur natürliche Zahlen einschließlich der Null sortiert werden und die Werte im Eingabearray dürfen eine gewisse Größe nicht überschreiten. Unter diesen Voraussetzungen ist dieses Verfahren, auch im ungünstigsten Fall, schneller als $\mathcal{O}(n \cdot log( n))$. Bei Countingsort handelt es sich um ein stabiles Sortierverfahren.
Das Sortierverfahren nutzt neben dem Eingabearray A[1…n] ein Ausgabefeld B[1…n] und ein Hilfsarray C[0…k]. Klein k enthält das Element mit der höchsten Wertigkeit, die im Eingabearray vorhanden ist. In der ersten for-Schleife, von Zeile 1-2, werden alle Einträge im Feld C auf 0 gesetzt. Jeder Index des Feldes C repräsentiert einen Wert, der im Eingabefeld vorhanden sein kann. Unter dem entsprechenden Index wird die Häufigkeit des Auftretens eines jeden Wertes festgehalten. Ist beispielsweise der Wert 2 im Eingabefeld 3 mal vertreten, dann wird unter dem Index 2 eine 3 festgehalten. Dieser Vorgang ist vergleichbar mit dem führen einer Strichliste. In den Zeilen 3-4 wird ermittelt mit welcher Häufigkeit jeder Wert vertreten ist. Von Zeile 6-7 wird das Feld C insofern bearbeitet, dass es die Anzahl der Elemente, die kleiner oder gleich dem Index sind, enthält. Dafür wird jeder Wert ab dem Index 2 mit seinem Vorgänger addiert. In den Zeilen 9-11 kann nun aus dem Feld C ermittelt werden, an welche Stelle des Ausgabearrays B jedes Element des Eingabearray A gehört. Wurde ein Element des Feldes A in das Feld B geschrieben, wird der Wert unter dem entsprechenden Index des Feldes C um eins reduziert.
Laufzeit
Zur Ermittlung der Laufzeit prüfen wir, welchen Beitrag jede der Iterationen zur Laufzeit leistet. Die for-Schleifen der Zeilen 1 und 6 sind von $k$ abhängig, tragen somit $\mathcal{O}(k)$ bei. Die der Zeilen 3 und 9 hängen von $n$ ab. Somit tragen diese $\mathcal{O}(n)$ bei. Die Gesamtlaufzeit ergibt sich aus der Summe aller Teillaufzeiten und entspricht somit $\mathcal{O}(n+k)$. Wenn k in $\mathcal{O}(n)$ ist, dann hat Countingsort eine Laufzeit von $\mathcal{O}(n)$. Die Unterschreitung der bisherigen Bestmarke von $\mathcal{O}(n \cdot log( n))$ ist nur möglich, weil keine Vergleichsoperationen ausgeführt werden müssen.
Übersicht Sortierverfahren
| Name | Best Case | Average Case | Worst Case | Stabil |
|---|---|---|---|---|
| Selection Sort | $\mathcal{O}(n^2)$ | $\mathcal{O}(n^2)$ | $\mathcal{O}(n^2)$ | nein |
| Insertion Sort | $\mathcal{O}(n)$ | $\mathcal{O}(n^2)$ | $\mathcal{O}(n^2)$ | ja |
| Mergesort | $\mathcal{O}(n \cdot log(n))$ | $\mathcal{O}(n \cdot log(n))$ | $\mathcal{O}(n \cdot log(n))$ | ja |
| Quicksort | $\mathcal{O}(n \cdot log(n))$ | $\mathcal{O}(n \cdot log(n))$ | $\mathcal{O}(n^2)$ | nein |
| Countingsort | $\mathcal{O}(n+m)$ | $\mathcal{O}(n+m)$ | $\mathcal{O}(n+m)$ | nein |
| Heapsort | $\mathcal{O}(n \cdot log(n))$ | $\mathcal{O}(n \cdot log(n))$ | $\mathcal{O}(n \cdot log(n))$ | nein |
Suchen
Die elektronische Speicherung von Daten ist aus der heutigen Welt nicht mehr wegzudenken. Das Auffinden abgelegter Daten und deren Manipulation ist ebenso wichtig. Oft müssen bestimmte Daten gefunden werden, die bestimmten Eigenschaften genügen müssen, die z.B. das Minimum oder Maximum einer Datensammlung darstellen. Der Anspruch der dabei an diese Algorithmen gestellt wird, ist ebenso groß, wie der an die Sortieralgorithmen gestellte. Die Art der zum Einsatz gebrachten Algorithmen, deren Arbeitsweise und die daraus erwachsenden Laufzeiten hängen davon ab, in welcher Art von Behälter (Datenstruktur) die Daten untergebracht sind und ob sie bereits einem Ordnungsprinzip unterliegen.
Zufallssuche
Die Zufallssuche ist ein Verfahren, bei dem auf ein zufällig gewähltes Datenobjekt zugegriffen wird. Diese Art der Suche ist nur in Datenstrukturen mit wahlfreiem Zugriff möglich und deren Einsatz macht nur Sinn, wenn die Daten keinem Ordnungsprinzip unterliegen. Datenstrukturen die an das Ablegen und an den Zugriff auf Daten spezielle Anforderungen stellen, können auf diese Weise nicht durchsucht werden. Darunter fällt z.B. die Warteschlange oder der Stack. Sie kann auf einem Feld ausgeführt werden. Die Zufallssuche wird praktisch nicht eingesetzt, weil es schnellere Verfahren gibt. Im ungünstigsten Fall müssen $n$ Vergleiche durchgeführt werden.
Lineare Suche
Bei der linearen Suche, auch sequenzielle Suche genannt, wird jedes Objekt der Datenstruktur vom kleinsten bis zum größten Index nacheinander durchsucht. Die Anwendung dieses Verfahrens ist nur sinnvoll, wenn die Daten keiner Ordnung unterliegen und die Anzahl der Objekte klein ist. Der Vorteil dieses Verfahrens ist, dass es auf jede Art von Behälter anwendbar ist. Im schlechtesten Fall muss der Schleifenkopf $n+1$ mal und der Schleifenkörper $n$ mal durchlaufen werden. Für den durchschnittlichen Fall kann von einer Anzahl von $\frac{n+1}{2}$ Durchläufen ausgegangen werden.
Binäre Suche
Die binäre Suche ist nur für Behälter mit wahlfreiem Zugriff einsetzbar und die abgelegten Objekte müssen sortiert sein. Beim Auffinden eines Objektes, z.B. eines Zahlenwertes in einem Feld A[1…n], wird folgendermaßen vorgegangen. Das zuerst untersuchte Objekt j befindet sich an der Position $\frac{n}{2}$. Entspricht es dem gesuchten Objekt, kann die Suche abgebrochen werden. Ist dies nicht der Fall, ist anhand der Wertigkeit des Objektes j festzustellen, ob sich das gesuchte Objekt links oder rechts von j befindet. In jedem Fall ist eines der entstandenen Teilfelder A[1…j-1] oder A[j+1…n] auf die gleiche Weise zu durchsuchen. Dies kann durch einen rekursiven Aufruf geschehen. Die maximale Anzahl von Schlüsselvergleichen ist aufgerundet $log_2(n+1)$. Im Mittel werden für große $n$ nicht mehr als $log_2(n+1)-1$ Vergleiche benötigt.
Binärer Suchbaum
Die Daten in einem binären Suchbaum unterliegen einem bestimmten Ordnungsprinzip. Angefangen beim Wurzelknoten, enthält der linke Kindknoten ein Element mit einer niedrigeren Wertigkeit und der rechte Kindknoten eines mit einer höheren Wertigkeit als der Wurzelknoten aufweist. Dieses Ordnungsprinzip ist auf den kompletten linken und rechten Teilbaum übertragbar. Alle Elemente links unterhalb des Wurzelknotens sind von einer geringeren Wertigkeit und die des rechten Teilbaumes von einer größeren Wertigkeit. Diese Organisation der Daten begünstigt das Auffinden eines gesuchten Elementes. Wird beispielsweise ein Element gesucht, das eine höhere Wertigkeit besitzt als das Wurzelelement, so kann sich dieses nur innerhalb des rechten Teilbaumes befinden. Das Auffinden des Elementes mit der höchsten oder niedrigsten Wertigkeit ist ebenfalls leicht zu organisieren. Das niederwertigste Element kann sich nach dem voran beschriebenen Ordnungsprinzip nur als Blattobjekt an der am weitesten links befindlichen Position befinden. Folgt man also der linken Kante, so stößt man auf dieses. Das Element mit der höchsten Wertigkeit kann analog dazu, entlang der rechten Kante gefunden werden.
In Abhängigkeit der Wertigkeit der unter dem Wurzelelement untergebrachten Daten kann die Höhe eines binären Baumes variieren. Zum einen kann der Baum ein ausgeglichenes, balanciertes Erscheinungsbild haben. Dies ist der Fall, wenn jeder Elternknoten immer zwei Kindknoten besitzt. Ein solcher Baum hat eine Höhe von $log_2 (n)$. Das andere Extrem ist ein Baum der nur linke oder rechte Kanten besitzt, jeder Elternknoten jeweils nur einen linken oder rechten Kindknoten hat. Diese Bäume haben folglich eine Höhe von $n$. Die verschieden Erscheinungsformen lassen erkennen, dass es in Abhängigkeit der gestellten Suchanfrage zu variierenden Laufzeiten kommen kann. Bei den möglichen Operationen dienen die Wurzelelemente als Schlüssel. Die Struktur der Bäume bietet auch hier eine rekursive Herangehensweise an. Die Anzahl der nötigen Schlüsselvergleiche entspricht für einen binären Suchbaum in ungünstigsten Fall der Höhe des Baumes. Somit ist auch die Laufzeit von $\mathcal{O}(h)$. Das ist für den balancierten Baum $\mathcal{O}(log_2 n)$ und für den unbalancierten $\mathcal{O}(n)$.
Fibonacci-Suche
Das Verfahren ähnelt sehr dem der binären Suche, unterscheidet sich aber in der Aufteilung der Eingabefolge. Diese wird nicht bei $\frac{n}{2}$ symmetrisch geteilt, sondern hier erfolgt die Teilung entsprechend der Folge der Fibonaccizahlen. Dieser Verfahren kommt ohne Divisionen aus, es werden nur Additionen und Subtraktionen verwendet. Die Aufteilung erfolgt nach folgender Definition:
$F_0 = 0,\; F_1 = 1,\; F_n = F_n-1 + F_n-2 \text{ für } (n \ge 2)$
Die Eingabefolge wird demnach in eine Teilfolge $F_n-2 -1$, ein Element i und zu der Teilfolge $F_n-1 – 1$ geteilt. Die Verfahrensweise bei den Vergleichen mit dem Schlüsselelement und der weiteren Zerlegung der entstehenden Teilfolgen ist analog zur binären Suche. Im ungünstigsten Fall müssen $\mathcal{O}(log_2(n))$ Vergleiche durchgeführt werden. Es kann nachgewiesen werden, dass der durchschnittliche Fall auch von der Ordnung $\mathcal{O}(log_2(n))$ ist.
Sprungsuche
Die Sprungsuche setzt genauso wie die binäre Suche eine sortierte Liste voraus. Hierbei wird die Liste zunächst in Sprüngen überflogen. Die Sprungweite kann dabei frei gewählt werden. Dabei wird der Abschnitt ermittelt, indem sich das gesuchte Element befinden sollte. Dies geschieht nach folgendem Ablauf:
- zerlegen der Liste in Abschnitte mittels der Sprünge
- Optimale Sprungweite: $\sqrt n$
- Prüfen ob sich das gesuchte Element darin befinden könnte
- Ist ein Abschnitt identifiziert, in dem sich das Element befinden könnte, wird dieser linear durchsucht
Beispiel
- Liste: (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16)
- gesuchtes Element: 12
- Sprungweite: 4
- 1. Abschnitt 1-5
- 2. Abschnitt 6-10
- 3. Abschnitt 11-15
- 4. Abschnitt 16
- Identifikation des Abschnittes in dem gesuchtes Element sein kann
- Da das gesuchte Element $< 11$ aber $> 15$ ist, sollte es im 3. Abschnitt liegen.
- Start der linearen Suche
- $11 \neq 12 \rightarrow 12 = 12$
- gesuchtes Element gefunden
Interpolationssuche
Die Interpolationssuche setzt nicht nur eine sortierte Liste voraus, sondern auch dass die darin befindlichen Daten einigermaßen gleich verteilt sind. Bei der Suche in der Liste muss zunächst der zu durchsuchende Bereich festgelegt werden. Dieser wird mittels $l$ für die linke und
$r$ für die rechte Grenze beschrieben. Das gesuchte Element erhält den Buchstaben
$v$. Dabei wird in der Liste mit dem Namen $A$ gesucht. Zur Berechnung der wahrscheinlichen Position wird
nun die Formel:
verwendet. Das Ergebnis $x$ ist nun die wahrscheinliche Position. Entspricht der Wert in
$A[x]$ nicht dem gesuchten Element, müssen 2. Fälle unterschieden werden.
Wert von $A[x]<v$
In diesem Fall muss die linke Grenze um $x$ und eins verschoben werden. Daraus ergibt sich
$l = x+1$. Anschließend muss die obige Formel erneut angewandt werden.
Wert von $A[x]>v$
In diesem Fall muss die rechte Grenze um $x$ und eins verschoben werden. Daraus ergibt sich
$r = x−1$. Anschließen muss die obige Formel erneut angewandt werden.
Beispiel
Liste: (1,2,3,5,7,11,13,15,21,26)
Gesuchtes Element: 11
Daraus ergiebt sich zunächst:
- $v=11$
- $l=1$
- $r=10$
Erste Anwendung der Formel:
Da $5<11$ muss nun die Linke Grenze verschoben werden.
Zweite Anwendung der Formel:
Gesuchtes Element wurde an der Position 6 gefunden.
Suchen nach dem Hash-Verfahren
- Kann nur Auskunft geben, ob Element in Liste vorhanden ist oder nicht.
- Vorrausetzung Hash-Tabelle der Liste
- erzeugen des Hashwertes des zu suchenden Elementes
- prüfen ob Platz in der Hashtable frei ist oder belegt
- wenn frei, dann gesuchter Wert nicht in der Liste
- wenn belegt, dann prüfen ob zugehöriges Element dem gesuchten entspricht, wenn das nicht der Fall ist, muss sondiert werden, solange bis das Element gefunden wurde oder man auf einen freien Platz stößt.
- Felder in denen mal ein Wert existiert hat, müssen gekennzeichnet werden, damit es bei der Suche nicht zu fehlerhaften Ergebnissen kommt.
Beispiel
Liste: (12, 61, 37, 85, 20, 19, 52, 24, 75, 38) Hashfunktion: Element mod 10
| Hash | Wert |
|---|---|
| 0 | 20 |
| 1 | 61 |
| 2 | 12 |
| 3 | 52 |
| 4 | 24 |
| 5 | 85 |
| 6 | 75 |
| 7 | 37 |
| 8 | 38 |
| 9 | 19 |
- Gesuchtes Element 75
- Hash wäre $5 \rightarrow $ lande bei $85 \rightarrow 85 \neq 75 \rightarrow $ Sondieren $\rightarrow $ lande bei $85 \rightarrow 85=85 \rightarrow $ Element gefunden.
Übersicht Suchverfahren
| Verfahren | Laufzeit | Vorraussetzugen |
|---|---|---|
| Lineare Suche | $\mathcal{O}( n )$ | Keine |
| Binär Suche | $\mathcal{O}( \log n )$ | Sortierte Daten |
| Interpolationssuche | $\mathcal{O}( \log ( \log n ))$ | Gleichmäßig verteilte Daten |
| Sprungsuche | $\mathcal{O}(\sqrt {n}) $ | Sortierte Daten |
| Hash-Verfahren | $\mathcal{O}( 1 )\; $bis$ \; \mathcal{O}( n )$ Abhängig von der Hash-Funktion | Hash-Table zu den Daten |
Suchen in Texten
Lineare Suche
Bei der linearen Suchen in Texten wird der Mustertext, ebenso wie bei der Suche in Listen, Zeichen für Zeichen mit dem zu durchsuchenden Text verglichen. Sobald ein Zeichen nicht mit dem Text übereinstimmt wird die Suchmaske um eins weiter gerückt.
Knuth-Morris-Pratt-Algorithmus
Der Knuth-Morris-Pratt Algorithmus ist eine verbesserte Version der linearen Suche in Texten. Dabei wird zunächst in der die Suchmaske (auch Suchtext genannt) nach Widerholungen des ersten Buchstabens gesucht. Zum Beispiel taucht in dem Wort "Kakao" das K an der 3. Stelle erneut auf. Das heißt, wenn in einem Text das Wort „Kakao“ gesucht werden soll und sich die Stellen bis zu dem 2. Kao gleichen, danach aber nicht mehr, kann das Muster um 2. Stellen verschoben werden.
Beispiel Kakao
| K | A | K | A | O |
|---|---|---|---|---|
| K | A | K | A |
| K | A | K | A | O |
|---|---|---|---|---|
| K | A | K |
| j | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Char | K | A | K | A | O | |
| Next[j] | -1 | 0 | 0 | 1 | 2 | 0 |
Beispiel
- Es soll in dem Text "AAKAAKAKAKAOKA" nach "KAKAO" gesucht werden
Vergleich
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | Bemerkung |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | A | K | A | A | K | A | K | A | K | A | O | K | A | |
| K | A | K | A | O | Mismatch an j=0, Next[0]= -1 | |||||||||
| K | A | K | A | O | Mismatch an j=0, Next[0]= -1 | |||||||||
| K | A | K | A | O | Mismatch an j=2, Next[2]= 0 | |||||||||
| K | A | K | A | O | Mismatch an j=0, Next[0]= -1 | |||||||||
| K | A | K | A | O | Mismatch an j=4, Next[4]= 2 | |||||||||
| K | A | K | A | O | Matched |
Boyer-Moore-Algorithmus
- Ähnlich der KMP Suche
- Vergleich von rechts nach links
- Sprungweite von 2 Methoden berechnet
1. Methode - Schlechte Zeichen Strategie
- Vergleich ist ein Zeichen das nicht im Suchmuster auftritt
- Muster kann um seine länge weiter geschoben werden
- Zeichen kommt im Muster vor
- Muster bis zu dem ersten Vorkommen des Zeichens von rechts verschieben
Beispiel
| Text | A | A | B | E | E | E | A | B | C | D |
|---|---|---|---|---|---|---|---|---|---|---|
| Muster | A | B | C | D |
| Text | A | A | B | E | E | E | A | B | C | D |
|---|---|---|---|---|---|---|---|---|---|---|
| Muster | A | B | C | D |
| Text | A | A | B | E | E | E | A | B | C | D |
|---|---|---|---|---|---|---|---|---|---|---|
| Muster | A | B | C | D |
Übersicht Textsuche
| Name | Laufzeit |
|---|---|
| Naiver Algorithmus | $m\cdot (n-m+1)$ |
| Knuth-Morris-Pratt Algorithmus | $2\cdot n+m$ |
| Boyer-Moore Algorithmus | $\frac {n}{m}$ |
Aufgaben
1. Suchen sie das Muster "ABRAKADABRA" in "ABRAKADABREABRAABRAKADABRAERG" mittels dem Knuth-Morris-Pratt Algorithmus und geben sie die Anzahl der benötigten verschiebungen an.
2. Suchen sie das Muster "WOHL" in dem Text "OTTO MOHL FÜHLT SICH WOHL MIT ATOMSTROM" mittels Boyer-Moore-Algorithmus und geben sie die Anzahl der benötigten Verschiebungen an.