Probabilistische Algorithmen WS13-14

Aus ProgrammingWiki

< AuK
Wechseln zu: Navigation, Suche

Loading

Inhaltsverzeichnis

Einleitung

Nachdem bereits theoretische Grundlagen zu Algorithmen sowie einige Beispiele vorgestellt wurden, geht es nun darum, diese zu verbessern. Laut Duden bedeutet probabilistisch "die Wahrscheinlichkeit berücksichtigend". In der Tat verzichtet man bei probabilistischen Verfahren auf vollständige Sicherheit. Dafür sind die Verfahren sehr effizient und elementar. Für die probabilistische Analyse ist es wichtig, Wissen über die Verteilung der Eingaben zu haben. Dies bringt uns zu probabilistischen oder auch randomisierten Algorithmen, deren Verhalten nicht nur von der Eingabe, sondern auch von Zufallszahlen abhängig ist. Denn zu wissen, dass die Eingaben zufällig erfolgen, ist besser als nichts über die Verteilung zu wissen. Als kleines Beispiel hierfür sei einführend das probabilistische Quicksort genant. Es ist bekannt, das der Worst-Case bei einer vorsortierten Liste auftritt, die Laufzeit dabei $\mathcal O(n^2)$ beträgt. Wählt man nun das Pivotelement zufällig, kann sich die Laufzeit hin zum Mittel verbessern, also $\mathcal O(n \log n)$. Da in den Verfahren Zufallszahlen genutzt werden, muss als erstes definiert werden, wie diese notwendige Funktion umgesetzt werden kann und welche Grenzen es dabei gibt. Danach werden verschiedene Gruppen probabilistischer Algorithmen vorgestellt und mit Beispielen erläutert. Abschließend wird die probabilistische Analyse, eine Methode zur Laufzeituntersuchung und zum Entwurf effizienter Algorithmen, vorgestellt.

Zufall

Was ist Zufall?

Auf der Suche nach der Definition des Begriffes Zufall liegt es nahe, die Wortbedeutung im Duden nachzuschlagen. Hier ist der Zufall als "etwas, was man nicht vorhergesehen hat, was unerwartet geschah" definiert. Hieraus ergibt sich die Fragestellung, ob das eingetretene Ereignis niemals vorausgesagt werden kann, oder nur in einem speziellen Fall nicht vorhergesehen werden konnte. Ein Beispiel: Wir betrachten den Wurf einer Münze, genauer gesagt den Zeitpunkt t, an welchem die Münze wieder beginnt, abwärts zu fallen. Das Ergebnis des Wurfes erscheint zufällig. Doch für einen begabten Mathematiker mit entsprechender Rechentechnik wäre es zum Zeitpunkt t durchaus möglich, anhand der Rotation, Umweltbedingungen und weiterer Parameter eine Vorhersage bezüglich des Ergebnis zu treffen. Er steht allerdings vor dem Problem, dass er das Ergebnis vor dem Auftreffen der Münze berechnen muss (Zeitfrage). Demnach ist eine Differenzierung nötig, da augenscheinlich sowohl die Perspektive des Betrachters eine Rolle spielt, als auch der Stand der Wissenschaft. Es existieren Ereignisse, von denen bewiesen werden konnte, dass sie keine kausale Ursache haben. Ein Beispiel hierfür ist der Zerfallszeitpunkt eines (radioaktiven) Atoms. Außerdem ist es möglich, dass man zwar alle Einflussfaktoren kennt, die ein Ergebnis bestimmen, diese aber weder ändern noch messen kann. Offensichtlich trifft dies bei Zufallsexperimenten zu. Betrachtet man den Wurf eines Würfels kann man sich leicht vorstellen, wovon das Ergebnis abhängt: Der angewendeten Kraft, dem Auftreffwinkel auf dem Untergrund, das Material des Untergrundes und des Würfels usw. Bevor man dies alles berücksichtigt hat, steht das Ergebnis schon fest. Dies entspricht auch dem Beispiel 1. Desweiteren kann es sein, dass die Ursache nicht erkennbar ist, aber existiert. Hierbei spricht man auch vom Pseudozufall. Dies findet in Programmiersprachen bei der Benutzung bestimmter Methoden Anwendung. Sie geben eine für den Betrachter ( = Programmierer) zufällige Zahl aus, unterliegen aber einer deterministisch definierten Berechnung.

Zufallszahlen erzeugen

Für die Erzeugung von Zufallszahlen gilt es also, die obigen Erkenntnisse zu berücksichtigen. Da man hierbei auf Beschränkungen trifft, haben erzeugte Zufallszahlen eine gewisse Güte. Es liegt nahe, bewiesene zufällige Ereignisse zu Verwenden, um Zufallszahlen von höchster Güte zu erzeugen. Diese sind allerdings immer physisch und nicht ohne Weiteres anwendbar, theoretisch gesehen ist allerdings die Verwendung beispielsweise des Atomzerfalls bestens geeignet. Ebenfalls physisch, leichter verwendbar und nur mit leicht geringerer Güte sind beispielsweise die Benutzung einer Lottomaschine oder das Werfen von Würfeln. Es ist offensichtlich, das diese Verfahren bei einer großen Zahl an gewünschten Zufallszahlen an (zeitliche) Grenzen stoßen. Um dieses Problem zu lösen gibt man sich mit Zufallszahlen geringerer Güte zufrieden und arbeitet mit Algorithmen, welche Pseudozufallszahlen erzeugen. Diese bezeichnen wir als Zufallszahlengeneratoren. Dieser Abschnitt erläutert die gebräuchlichste Methode zur Erzeugung von Zufallszahlen sowie deren Verwendung. Desweiteren werden Algorithmen für die Erzeugung spezieller Zufallszahlen vorgestellt und Hinweise zur Implementierung gegeben.

Lineare Kongruenzmethode

Dies ist die am häufigsten genutzte Methode, um (pseudo)zufällige Zahlen zu erzeugen, gleichfalls ist es eine sehr alte. Derrick H.Lehmer entwickelte sie 1948, da die bis dahin genutzte Mittquadratmethode (von Neumann) noch nicht optimal war. Lehmers lineare Kongruenzmethode dagegen ist nicht nur sehr einfach zu implementieren und sehr schnell in der Berechnung, sondern erzeugt auch qualitativ hochwertige Zufallszahlen, wenn sie richtig angewandt wird. Als Grundlage dient die folgende Gleichung. 

\[ x_{n+1} = ( a \cdot x_{n} + c) \bmod m \]

$c$ bezeichnet man als Inkrement, $a$ als Multiplikator, $x_{0}$ als Seed und $m$ als Modul. Für diese Werte gelten (einführend) die folgenden Bedingungen.

\begin{equation} m > 0 \end{equation} \begin{equation} 0 \leq a < m \end{equation} \begin{equation} 0 \leq c < m \end{equation} 

Übungsaufgabe: Gegeben sind $a = 4$, $c = 6$, $m = 21$ und $x_{0}=3$. Berechnen Sie die ersten 6 Folgeglieder.

Es wird deutlich, dass die Folge periodisch verläuft, was nicht gewollt ist. Dieses Ergebnis ergibt sich aus der Wahl der Parameter, weshalb weitere Eigenschaften festgelegt werden müssen. An das Modul $m$ stellen wir die Anforderung, möglichst groß zu sein. Praktisch bedeutet dies, dass die größte zur Verfügung stehende Integer-Zahl verwendet wird ($(2^{32})-1$). Beweisen lässt sich diese Bedingung durch die Eigenschaft der Modulorechnung beziehungsweise der ganzzahligen Division mit Rest. Es gilt für $\ a\ =\ b\bmod\ c$, dass es keine Restklasse größer oder gleich $c$ gibt: $\ 0 \leq\ a\ \leq\ c-1$. Trotz großer $m$ kann es zu einer kleinen Periodenlänge kommen, der Zufallszahlengenerator ist also ungünstig. Auch dies ist den Parametern geschuldet. Ein Beispiel sei gegeben mit $a=4$, $c=6$, $x_{0}=3$, $m=100$. Die Folgeglieder sind $x_{1}=18$, $x_{2}=78$, $x_{3}=18$ usw. Weitere Bedingungen sind notwendig, um eine optimale Folge, d.h. eine mit möglichst großer Periodenlänge, zu erhalten. \begin{equation} ggT\ (c,m) = 1 \end{equation} \begin{equation} a \bmod q = 1\text{, für jeden Elementarteiler (Primfaktor) q von }m \end{equation} \begin{equation} a \bmod 4 = 1\text{, falls 4 Teiler von }m \end{equation}

Ein Beispiel für $m=100$:

  • Primfaktorzerlegung für $100$: $2\cdot 2 \cdot 5\cdot 5$
  • Bedingung 1 erfüllen: $c$ muss auf $1$, $3$, $7$ oder $9$ enden
  • Bedingung 2 erfüllen: $ a\ \bmod\ 2\ =\ 1$ und $a\ \bmod\ 5\ =\ 1\ \rightarrow \ a \in\ \{1,11,21,31,41,51,61,71,81,91 \}$
  • Bedingung 3 erfüllen: $a\ \bmod\ 4\ =\ 1\ \rightarrow\ a\ \in\ \{1,21,41,61,81 \}$

Diese Voraussetzungen hat Donald E. Knuth 1997 mathematisch bewiesen und veröffentlicht. Daraus ergeben sich optimale Parameterkonstellationen, beispielsweise $a=61$ und $c=89$. Probieren Sie es in den Übungen aus! Weiterhin befasste sich Robert Sedgewick mit dem Einfluss der Parameter auf die Kongruenzmethode und veröffentlichte 2002 Regeln zur Anwendung dieser. Diese überschneiden sich mit den bereits eingeführten, beispielsweise die Wahl eines großen Moduls oder den Wert $1$ für das Inkrement. Erweiternd fügte er hinzu, dass der Multiplikator ungefähr eine Zehnerpotenz kleiner sein sollte als das Modul. Desweiteren existieren Verfahren, welche die Periodenlänge noch weiter verlängern. Diese seien nur erwähnt und können bei Interesse nachgearbeitet werden: Die sogenannte Tabellenmethode von MacLaren und Marsaglia oder die Schieberegistermethode von Tausworthe. Die Länge der Periode kann dadurch so stark erhöht werden, dass der Begriff Periodenlänge eigentlich nicht mehr verwendbar ist.

Zwischenstand

Wir sind in der Lage, deterministisch Zufallszahlenfolgen mit möglichst großer Periodenlänge zu erzeugen. Anhand des Seeds, also des Startwertes, wählen wir einen Bereich dieser Periode aus. Dabei kann eine Zahl nicht doppelt vorkommen, da dies eine Wiederholung der Periode bedeuten würde. Desweiteren können wir noch kein Intervall angeben, in dem die Zufallszahlen liegen sollen.

Gleitkommazufallszahlen

Es kann notwendig sein, Zufallszahlen im halboffenen Intervall $[0\dots 1)$ zu erzeugen (Wertebereich: $0\leq x < 1$). Sowohl für weitere Zufallszahlengeneratoren als auch für mathematische Methoden, beispielsweise für die näherungsweise Berechnung von $\pi$ mit der Zufallsregenmethode, benötigt man zufällige Gleitkommazahlen. Der Algorithmus kann leicht unter Verwendung der linearen Kongruenzmethode angegeben werden, wobei randint() wie obige kongruenz-Methode funktioniert, aber eine Zufallszahl nach der anderen zurückgibt.


Dabei wird lediglich die erzeugte Zufallszahl durch das Modul dividiert.

Hinweis:

Die Variable start dient dabei zur Zwischenspeicherung der $x_{n}$ Werte. Es werden also Algorithmen mit Gedächtnis genutzt, d.h. sie können auf bereits berechnete Werte zugreifen. In der Programmiersprache C++ könnte man dies durch eine statische Variable innerhalb der Methode umsetzen, in Java ist hierfür eine Klassenvariable notwendig.

Zufallszahlen im Intervall

Intervallbezogene Zufallszahlen werden wohl am häufigsten genutzt, da sich für die meisten Zufallsexperimente Grenzen angeben lassen. Beispielsweise kann bei einer Münze keine dritte Seite und bei einem fairen Würfel keine sieben auftreten. Als Hilfsfunktion wird die oben definierte randReal()-Methode verwendet. Desweiteren wird die Floor-Methode benötigt, welche in der Einführungsveranstaltung vorgestellt wurde. Zur Erinnerung: Die Floor-Methode liefert eine Zahl $max(y) \leq x, y \in \mathcal Z$,$x \in \mathcal R$, d.h. Floor() rundet immer ab. In die Variable n wird das Intervall gespeichert, in dem die Zufallszahl liegen darf. Die Addition mit $1$ ist nötig, um die obere Intervallgrenze als mögliche Zufallszahl nicht auszuschließen. Eine Zufallszahl zwischen $0$ und $1$ wird mit dem Intervall multipliziert, wodurch eine Zahl entsteht, die nicht größer als das Intervall sein kann. Durch die Addition der unteren Grenze erhält man die Zahl im gewünschten Intervall.

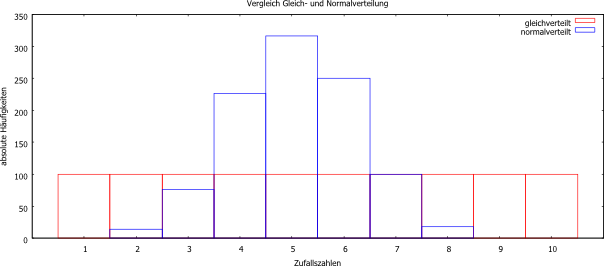
Wichtig zu erwähnen ist, dass die Zufallszahlen, die hier erzeugt werden, gleichverteilt sind. Das bedeutet, jede Zahl hat immer die gleiche Wahrscheinlichkeit des Auftretens. Überprüfen kann man dies durch Erzeugung einer Folge von Zufallszahlen in einem festgelegten Intervall und Zählung der absoluten Häufigkeiten der aufgetretenen Zahlen. Diese Art der Verteilung ist aber unter Umständen nicht erwünscht, beispielsweise für statistische Auswertungen. Dies erfordert eine Erweiterung, welche im folgenden Abschnitt vorgestellt wird.

Normalverteilte Zufallszahlen

Mitunter ist es nicht sinnvoll, gleichverteilte Zufallszahlenfolgen zu benutzen. Ein Beispiel ist die Körpergröße von Menschen, nicht alle Größen sind gleich Wahrscheinlich, die durchschnittliche Körpergröße (Männer: 178cm, Frauen: 165cm) tritt häufiger auf als andere. Derartige Verteilungen bezeichnet man auch als Gaußverteilung. Zur Bildung des Algorithmus verwenden wir den zentralen Grenzwertsatz der Statistik. Eigentlich sind es mehrere Sätze, doch hier reicht die Kernaussage. Die Summe unabhängiger Zufallszahlen folgt asymptotisch einer stabilen Verteilung. Ist die Varianz der Zufallszahlen endlich und positiv, ist die Summe normalverteilt. Diese Aussagen reichen aus, um einen Algorithmus zu schreiben, der normalverteilte Zufallszahlen liefert. Es werden mehrere gleichverteilte Zufallszahlen (wir benutzen unsere Methode rangeRandReal()) und deren Durchschnitt gebildet. Dieser entspricht dem neuen Folgeglied der normalverteilten Folge. Nach dem Grenzwertsatz müssten dafür sehr viele gleichverteilte Zufallszahlen aufsummiert werden, Donald E. Knuth hat jedoch 1997 bewiesen und veröffentlicht, das es ausreichend ist, $6$ bis $10$ Zahlen zu verwenden.

S3rostri Verteilung.png

In der obigen Abbildung ist das Ergebnis einer Häufigkeitszählung für erzeugte Zufallszahlen zu sehen. Verwendet wurde der Algorithmus rangeRandReal() für die gleichverteilten Zufallszahlen und für die Normalverteilung rangeRandGauss(). Man erkennt deutlich die Ähnlichkeit der Normalverteilung mit der Gaußschen Glockenkurve. Jede Art der Verteilung hat ihre Einsatzbereiche, wobei im weiteren Verlauf nur die gleichverteilten Zufallszahlen eine Rolle spielen. Normalverteilte Zufallszahlen werden häufig im Bereich der Statistik angewandt.

Gütetests für Zufallszahlen

Es ist nicht Aufgabe dieses Abschnittes, die verschiedenen Testverfahren für die Güte von Zufallszahlen im Detail zu erläutern. Er ist eher informativ und dient der Anregung des Selbststudiums. Als Hinweis sei hier das Werk "The Art of computer programming" von Donald E. Knuth aus dem Jahr 1997 empfohlen. Ein möglicher Test wirkt etwas seltsam, ist aber gut geeignet, Muster in Zufallszahlen zu entdecken. Beim so genannten Himmelstest werden die erzeugten Zufallszahlen als Punkte in einem Koordinatensystem dargestellt. Jetzt betrachtet man dieses Koordinatensystem und nutzt die Fähigkeit des menschlichen Auges, Muster zu erkennen. Dies bezeichnet man auch als visuellen Test. (Achtung: Immer große Anzahlen von Zufallszahlen nutzen, da Häufungen bei kleinem $n$ dem Zufall entsprechen). Ein weiterer Test wird als Häufigkeitstest bezeichnet, bei welchem dem Name entsprechend die absoluten Häufigkeiten betrachtet werden. Beim Serientest betrachtet man nicht das Auftreten einzelner Zahlen, sondern das von Zahlenpaaren und beim Lückentest untersucht man die Abstände, in denen sich Zufallszahlen wiederholen. Nicht unterschlagen werden soll der $\lambda^2$-Test, mit dem überprüft werden kann, ob die generierten Zufallszahlen einer bestimmten Verteilung entsprechen. Auch Robert Sedgewick hat auf diesem Gebiet gearbeitet und das Verfahren durch Angabe einer einfachen Formel zur Grenzwertberechnung für $\lambda^2$ verbessert.

Fazit

In diesem Abschnitt wurde erläutert, was Zufall eigentlich bedeutet und wie man ihn nachahmen kann. Damit wurde der Begriff des Pseudo-Zufalles eingeführt und die gebräuchlichste Methode zur Berechnung von Zufallszahlenfolgen mittels eines Computers vorgestellt. Desweiteren wurden Anwendungshinweise für diese Methode erläutert sowie Schwächen aufgezeigt. Die Vorteile wurden weiter ausgebaut, um die erhaltenen Zufallszahlen weiteren praktischen Sachverhalten zu erschließen, beispielsweise die Möglichkeit, Zufallszahlen nur in einem bestimmten Intervall zu erzeugen. Es wurde auf die Besonderheit der Gauss- oder Normalverteilung im Vergleich zur Gleichverteilung hingewiesen und ein Algorithmus vorgestellt, der in der Lage ist, diese Verteilung umzusetzen. In den folgenden Abschnitten werden die Erkenntnisse angewandt und die erstellten Algorithmen verwendet.

Numerisch probabilistische Algorithmen

Definition

Numerisch probabilistische Algorithmen geben als Ergebnis eine Näherungslösung mit wählbarer Genauigkeit zurück. Dadurch kann der Nutzer mit der Wahl seiner Eingaben bestimmen, wie genau das gewünschte Ergebnis sein soll. Sie werden numerisch probabilistisch genannt, da in den Algorithmen mit Berechnungen und dem Zufall gearbeitet wird. Aufgrund der Nutzung des Zufalls ist diese Art von Algorithmen nichtdeterminiert, dass bedeutet das bei mehrfacher Ausführung mit dem gleichen Wert unterschiedliche Lösungen zurückgegeben werden können. Nichtdeterministische Algorithmen können auch nicht determinierend sein, müssen jedoch nicht zwingend. Eine deterministischer Algorithmus, ist determinierend, wenn er Seiteneffekt frei ist.

Beispiel: Zufallsregen

Eine einfache Art der Bestimmung eines Näherungswertes für ist die Methode des sogenannten Zufallregens.
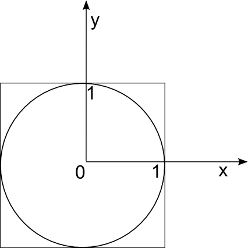
S3damuel Regen-pi-sw2.png
Man werfe dabei eine beliebige Anzahl an "Regentropfen" auf das oben abgebildete Quadrat mit Innenkreis, wobei der Radius des Innenkreises den Wert 1 besitzt. Um zu bestimmen werden zwei Arten von aufkommenden Tropfen gezählt: die Tropfen innerhalb des Kreises und die Tropfen innerhalb des Quadrates . Um die Genauigkeit der Berechnung zu erhöhen, betrachtet man nur die Tropfen im ersten Quadranten der Quadrates. Damit ein Punkt innerhalb des Kreises liegt gelten für ihn folgende Bestimmungen: $x^2+y^2 \le 1$, wobei $x,y$ reelle Zahlen im Bereich $0 < x,y \le 1$.
Die Annäherung an $\pi$ ergibt sich dann aus folgenden Überlegungen:
\begin{equation}\frac{A_{Kreis}}{A_{Quadrat}} = \frac{\pi r^2}{4r^2} \approx \frac{T_{Kreis}}{T_{Quadrat}}\end{equation}


Da zunächst nur das Auftreffen im ersten Quadranten betrachtet wurde, ergibt sich nun nach folgender Operation der Näherungswert für $\pi$:
\begin{equation}\pi = 4 * \frac{T_{Kreis}}{T_{Quadrat}}\end{equation}.

Die folgende Java-Prozedur rain(int anzahl) soll verdeutlichen, wie sich der Zufallsregen bei einer bestimmten Anzahl an Tropfen für die Bestimmung von $\pi$ verhält.

Mit Hilfe einer kleinen Schleife, welche die Differenz zwischen $\pi$ und unserem Ergebnis von rain(int anzahl) ausgibt kann nachgewiesen werden, dass Näherungswerte für $\pi$ ermittelt werden und der Algorithmus nichtdeterminierend arbeitet.

Zwischenstand

Es wurde gezeigt, dass numerisch probabilistische Algorithmen eine wählbare Genauigkeit besitzen. Im Beispiel kann die Genauigkeit durch steigende Tropfenanzahl verbessert werden. Mit dieser Methode des Zufallsregens lassen sich auch weitere Flächen aus Verhältnissen berechnen, so z.B. jedes beliebige bestimmte Integral.

In den nun folgenden Abschnitten werden zwei spezielle Teilgruppen von probabilistischen Algorithmen vorgestellt.

Las-Vegas-Algorithmen

Gehört ein Algorithmus zur Gruppe der Las-Vegas-Algorithmen, so gibt dieser niemals ein falsches Ergebnis zurück. Um dies zu gewährleisten wird in einigen Fällen kein Ergebnis geliefert, da der Algorithmus niemals endet. Den Zeitpunkt, zu welchem man den Aufruf als gescheitert ansieht, kann man selbst bestimmen. Durch erneuten Aufruf (da probabilistisch mit wahrscheinlich anderem Zufallswert) steigt die Wahrscheinlichkeit, ein Ergebnis zu erhalten.

Aufwandsanalyse für Las-Vegas-Algorithmen

Man betrachtet den Aufruf eines beliebigen, in diesem Falle einstelligen Las-Vegas-Algorithmus LV(x) welcher das Ergebnis y und einen Wahrheitswert Erfolg liefert. Erfolg nimmt je nach Ausführung einen der beiden möglichen Wahrheitswerte an und im Falle einer erfolgreichen Ausführung nimmt y den Wert des Ergebnisses an. Weiterhin wird für die Analyse die Wahrscheinlichkeit betrachtet, dass eine Lösung für den Eingabewert x ausgegeben wird. Sie wird angegeben als $0 < p(x) < 1$. Um festzulegen, ob der Algorithmus noch arbeitet oder kein Ergebnis mehr liefern wird, ist es wichtig eine Zeit failure(x) festzulegen. Wird diese Zeit überschritten so gilt der Durchlauf als gescheitert und Erfolg erhält den Wert false. Eine andere Zeit success(x) beinhaltet den Zeitwert bis das richtige Ergebnis ausgegeben wurde. In einer Schleife wird der Prozeduraufruf so oft wiederholt, bis ein Ergebnis zurückgegeben wurde.

Will man berechnen wie lange eine derartige Schleife laufen würde, kann folgende Formel angewandt werden: \[ t(x) = p(x) \cdot success(x) + (1 - p(x)) \cdot (failure(x) + t(x)) \] Durch Umformung erhält man die Formel: \[ t(x) = success(x) + \left( \frac{1}{p(x)} -1\right) \cdot failure(x) \]

Welchen Einfluss haben die einzelnen Faktoren auf die Rechenzeit?

Die Rechenzeit besteht aus der Zeit, die für den erfolgreichen Aufruf gebraucht wird und der Zeit, die für erfolglose Aufrufe gebraucht wird. Das Ziel muss es also sein, die Zeit der erfolglosen Aufrufe zu minimieren um auch insgesamt die Rechenzeit zu minimieren. Diese Zeit wird durch die Wahrscheinlichkeit für den Erfolg und die Zeit bis zum Abbruch beeinflusst, will man sie minimieren so ist dies durch eine hohe Wahrscheinlichkeit möglich. Allerdings wird eine hohe Wahrscheinlichkeit durch einen höheren Wert der Abbruchzeit erreicht, denn je länger der Algorithmus Zeit hat um zu arbeiten, desto wahrscheinlicher ist es, dass ein Ergebnis zurückgegeben werden kann. Der Nutzer muss sich also für einen Zwischenwert von geringer Erfolgswahrscheinlichkeit und längerer Arbeitszeit des Algorithmus entscheiden, wenn er die Rechenzeit reduzieren möchte.

Sherwood-Algorithmen

Die Sherwood-Algorithmen sind eine spezielle Teilgruppe der Las-Vegas-Algorithmen, denn diese liefern immer ein richtiges Ergebnis - den Fall, dass der Algorithmus nicht endet, gibt es nicht. Diese Algorithmen werden aus deterministischen Verfahren erstellt, welche im mittleren Fall viel effizienter arbeiten als im schlechtesten Fall. Um diesen Unterschied zu minimieren wird ein Zufallselement gewählt, so dass sich der Algorithmus im Mittel weiter wie das Original verhält, jedoch schlechte Elemente so verändert werden, dass sich ebenfalls der mittlere Aufwand ergibt. Diese Veränderung bezeichnet man auch als Robin-Hood-Effekt. Ein Beispiel für Sherwood-Algorithmen wäre das probabilistische Quicksort, bei dem das Pivotelement immer zufällig aus der Liste gewählt wird.

Zwischenstand

Las-Vegas-Algorithmen liefern entweder ein richtiges oder kein Ergebnis. Sollten sie kein Ergebnis liefern, so kann man durch erneuten Aufruf doch noch ein Ergebnis erhalten. Als Sonderfall können Sherwood-Algorithmen betrachtet werden, welche immer ein korrektes Ergebnis liefern.

Monte-Carlo-Algorithmen

Monte-Carlo-Algorithmen sind eine Art von Algorithmen die zwar oft das richtige Ergebnis ausgeben, selten jedoch Fehler zulassen können. Diese Fehler sind keine Näherungswerte, sondern komplett falsch. Da beim Aufruf im Allgemeinen jedoch keine Lösung vorhanden ist, kann man auch nicht beurteilen ob das Ergebnis richtig ist oder sich der Algorithmus geirrt hat. Man kann nicht davon ausgehen, dass der Algorithmus bei den meisten Aufrufen ein richtiges Ergebnis liefert.

In den folgenden Abschnitten sollen einige Beispiele für diese Algorithmenart behandelt werden.

Primzahltest nach Fermat

Auf Grundlage des "kleinen Satzes von Fermat" gelingt es, einen Algorithmus zu schaffen, der feststellt ob eine Zahl keine Primzahl oder wahrscheinlich eine Primzahl ist.

Theoretische Grundlage (Euler):
Für alle natürlichen Zahlen $n$ und $a$ mit $n \ge 2$ und $1 \le a \le n$, wobei $ggT(a,n) = 1$ (teilerfremd), gilt $a^{\phi (n)} \equiv 1 \bmod n$. Speziell für Primzahlen gilt: $\phi(n) = n-1$ laut Definition. 

Wenn $n$ eine Primzahl ist, dann gilt für alle Zahlen $a$ (mit $1 \leq a \leq n-1)\ \ a^{n-1} \equiv 1 \bmod n$ (Kleiner Satz von Fermat)
Dabei muss die Bedingung gelten: $ggT(a,n)= 1$

Verlauf des Primzahltests

Der Test wird durchgeführt für eine natürliche Zahl $n$. Als Ergebnis erhält man entweder die Aussage, dass die Zahl keine Primzahl ist oder das keine Aussage über die Zahl getroffen werden kann. Es wird eine Basis $a$ gewählt, für welche die Bedingung $1 < a < n$ gilt und für die beiden Zahlen getestet, ob diese teilerfremd sind. Nun können drei Fälle eintreten:

  • $ggT(a,n) \neq 1$ $\rightarrow$ keine Primzahl
  • $a^{n-1} \not \equiv 1 \bmod n$ $\rightarrow$ keine Primzahl
  • $\rightarrow$ keine Aussage

Wenn der Test mit mehreren verschiedenen Basen ausgeführt wurde und es kam immer zu dem Ergebnis, dass keine Aussage möglich ist, so kann man feststellen, dass die Zahl vermutlich eine Primzahl ist.

Um den folgenden Algorithmus ausführen zu können benötigen wir eine Prozedur ggT, welche zwei Zahlen erwartet und als Ergebnis den größten gemeinsamen Teiler zurückgibt. In unserem Fall setzen wir diese Prozedur als vorhanden voraus, so dass an dieser Stelle eine Definition entfällt.

Dieser Code ist hier, aufgrund der Datentypen in Java nur für die Zahlen bis 151 ausführbar, will man den Primzahltest auch für größere Zahlen ausführen, so muss man schon vorher die Zahlen mit Hilfe der Modulooperation verändern.

Pseudoprimzahlen - Carmichaelzahlen

Warum ist keine Aussage möglich, wenn keine der ersten beiden Bedingungen zutrifft?
Man kann durch den Test mit einer Basis keine endgültige Entscheidung treffen, da es Basen gibt, für welche beide Bedingungen nicht gelten, obwohl die Zahl keine Primzahl ist. Vom Programm würde man das Ergebnis erhalten, dass keine Aussage möglich sei.
Ein Beispiel dafür wäre die Zahl $645$. Es gilt:

  • $645 = 5 \cdot 131$ jedoch auch
  • $ggT(2,645)=1$ und $2^{644} \equiv 1 \bmod 645$

für die Untersuchung mit der Basis 2. Zahlen dieser Art, welche für eine bestimmte Basis den Test erfüllen, nennt man fermatsche Pseudoprimzahlen. Bis zum Wert 2000 gibt es 303 echte Primzahlen, jedoch nur 7 Pseudoprimzahlen zur Basis $2$ nach dem Test von Fermat.
Es gibt jedoch auch Zahlen, die den Test mit jeder gewählten Basis bestehen und dennoch keine Primzahlen sind. Diese nennt man Carmichaelzahlen. Von ihnen gibt es bis zum Wert 2000 gerade einmal 3.

Miller-Rabin-Test

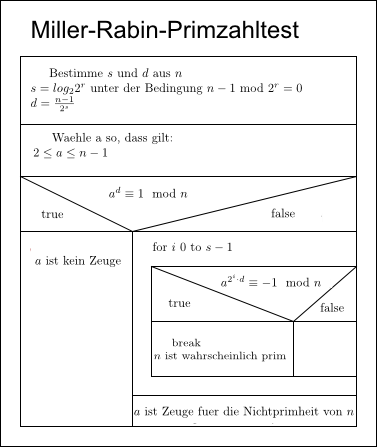
Wie schon der Primzahltest von Fermat nimmt auch der Miller-Rabin-Test eine Testzahl $n$ und gibt dafür zurück, ob die Zahl keine Primzahl oder wahrscheinlich Primzahl ist. Um den Algorithmus anwenden zu können ist zunächst die Bestimmung zweier Zahlen $s$ und $d$ aus der Eingabezahl $n$ notwendig:

Miller-Rabin-Primzahltest Ablauf

\[ s= \log_2 2^r \text{unter der Bedingung } (n-1)\bmod 2^r= 0 \]Daraus folgt, dass $r = s$. Um den Wert für $d$ zu bestimmen wird folgende Formel angewendet: \[d = \frac{n-1}{2^s}\]. 

Übungsaufgabe: Berechnen Sie $s$ und $d$ für den Primzahltest für $821$.

Um den Ablauf des Algorithmus für diesen Primzahltest zu verdeutlichen wird hier ein Nassi-Shneiderman-Diagramm angegeben.

Primzahltest nach Solovay und Strassen

Durch den Primzahltest von Solovay und Strassen kann ein Algorithmus geschrieben werden, welcher mit Hilfe einer Zahl $a$, für welche $a < n$ und $ggT(a,n)=1$ gilt, bestimmt, ob eine Zahl $n$ prim ist. Dazu wird das Jacobisymbol $\mathcal{J}(a,n)$ zweier Zahlen bestimmt, welches rekursiv dargestellt werden kann. \begin{equation} \mathcal{J}(a,n) =\begin{cases} 1 & \text{falls $a = 1$}\\ \mathcal{J}(\frac{a}{2},n) \cdot (-1)^{\frac{n^2-1}{8}} & \text{falls $a$ gerade}\\ \mathcal{J}(n \bmod a,a) \cdot (-1)^{(a-1)\cdot {\frac{n-1}{4}}} & \text{sonst} \end{cases}\end{equation} Das Jacobisymbol nimmt immer den Wert $-1$ oder $1$ an. Um dies zu erreichen muss gelten, dass $n \in \mathcal{N}$ und $n$ ungerade. Diese Einschränkung für $n$ ist einerseits leicht mathematisch zu beweisen und andererseits leicht erkennbar, da die einzige gerade Primzahl $2$ ist und somit im Test extra betrachtet werden kann.


Für diese zwei Zahlen gilt nun folgender Satz: 

Wenn $n$ eine Primzahl ist, dann gilt für alle $a \in \mathcal{N}$ (mit $1 \leq a \leq n-1$ und $ggT(a,n)=1)$ $\mathcal{J}(a,n)$ $\equiv a^{\frac{n-1}{2}} \bmod n$.

Ein möglicher Algorithmus für einen solchen Primzahltest könnte folgendermaßen aussehen:

Die Prozedur jacobi(a,n) beschreibt dabei die Anwendung des Jacobisymbols.

Wenn $n$ keine Primzahl ist, so kann nachgewiesen werden, dass maximal die Hälfte aller Zahlen $a < n$ die Bedingung erfüllen. Dies bedeutet, dass wenn der Test positiv ausfällt, die Wahrscheinlichkeit dafür, dass $n$ eine Primzahl ist, größer als $0,5$ ist. Doch warum erfüllen so viele Zahlen die Bedingung nicht? Eine nichtprime Zahl hat nur einen gewissen Anteil an möglichen Zahlen für $a$, so dass der ggT 1 ist. Alle $a$ für welche diese Bedingung nicht gelten, werden falsche Zeugen genannt. Auch hier, ähnlich wie beim Primzahltest von Fermat, gilt, dass bei mehrfachem Aufruf mit positivem Ergebnis die Chance dafür steigt, dass $n$ eine Primzahl ist. Jedoch ist in diesem Test die Wahrscheinlichkeit für ein richtiges Ergebnis im Vergleich zum Fermatischen Primzahltest höher, da auch für fermatische Pseudoprimzahlen festgestellt wird, dass dies keine Primzahlen sind.

Fazit

In diesem Kapitel wurde anhand von drei Primzahltests unterschiedlicher Güte die Anwendung von Monte-Carlo-Algorithmen dargestellt. Da es möglich ist, dass diese Algorithmen falsche Ergebnisse zurückgeben, kann nur festgestellt werden, ob eine Zahl keine Primzahl ist oder eventuell Primzahl ist. Der Begriff der Pseudoprimzahlen wurde eingeführt, welche durch eben solche falschen Ergebnisse entstehen können. Die Anwendung des Jacobisymbols wurde ebenso erläutert wie die Berechnung der benötigten Grundlagen für den Miller-Rabin-Test.

Probabilistische Analyse

Dieses Verfahren dient sowohl der Analyse der Laufzeit eines Algorithmus als auch dem Entwurf für effiziente Algorithmen. Dazu ist es nötig, Wissen über die Verteilung der Eingaben zu haben. Legt man diese zufällig fest mittelt man sozusagen die Laufzeit über alle Eingaben. Die Analyse nutzt dabei nur gleichverteilte Zufallszahlen, siehe Zufallszahlen erzeugen. Man verwendet zur Analyse so genannte Indikatorfunktionen, die im folgenden Abschnitt vorgestellt werden.

Indikatorfunktionen

Diese Funktionen beschreiben den Übergang zwischen Erwartungswerten und Wahrscheinlichkeiten. Als Voraussetzung betrachten wir einen gegebenen Wahrscheinlichkeitsraum $S$ und ein Ereignis $A$. Die Indikatorfunktion $I\{ A\}$, welche mit dem Ereignis verknüpft ist wird definiert durch \begin{equation} I\{ A\}=\begin{cases} 1 & \text{falls A eintritt}\\ 0 & \text{falls A nicht eintritt} \end{cases} \end{equation} Als Beispiel verwenden wir den Wurf eines Würfels. Der Wahrscheinlichkeitsraum ist $S=\{ 1,2,3,4,5,6\}$ mit $Pr\{ 1\} =Pr\{ 2\} =Pr\{ 3\} =Pr\{ 4\} =Pr\{ 5\} =Pr\{ 6\} =\frac{1}{6}$. Es soll eine Indikatorfunktion $X_1$ definiert werden, welche mit dem Ereignis "Eine $1$ wird gewürfelt" verknüpft ist. \begin{equation} X_1=I\{ 1\}=\begin{cases} 1 & \text{falls 1 eintritt}\\ 0 & \text{falls 2,3,4,5,6 eintritt} \end{cases} \end{equation}

Die erwartete Anzahl, mit der das Ereignis "Eine $1$ wird gewürfelt" eintritt, ist der Erwartungswert der Indikatorfunktion $X_1$.

\begin{equation} E[X_1]=E[I\{ 1\}] \end{equation} \begin{equation} =1\cdot Pr\{1\} + 0\cdot Pr\{ 2\} + 0\cdot Pr\{ 3\} + 0\cdot Pr\{ 4\} + 0\cdot Pr\{ 5\} + 0\cdot Pr\{ 6\} \end{equation} \begin{equation} =1 \cdot \frac{1}{6} + 5\cdot ( 0 \cdot \frac{5}{6}) \end{equation} \begin{equation} =\frac{1}{6} \end{equation}

Desweiteren ist der Erwartungswert dieser Indikatorfunktion $X_1$ gleich der Wahrscheinlichkeit für das Eintreten des mit dieser Funktion verknüpften Ereignisses, im Beispiel für "Eine $1$ wird gewürfelt". Dies lässt sich allgemein als Lemma formulieren und beweisen. 

Für einen gegebenen Wahrscheinlichkeitsraum $S$ und ein Ereignis $A \in S$ mit $X_A = I\{A \}$ gilt: $E[X_A]=Pr\{ A\}$


\begin{equation} E[X_A]=E[I\{ A\}] \end{equation} \begin{equation} =1 \cdot Pr\{ A\} + 0 \cdot Pr\{ \bar{A}\} \end{equation} \begin{equation} =Pr\{ A\} \end{equation}

$\bar{A}$ ist das Komplement von $A$, im Beispiel also $\{ 2,3,4,5,6\}$.

Für dieses Beispiel scheint die Indikatorfunktion ein wenig zuviel des Guten zu sein, doch für wiederholte Zufallsversuche ist sie sehr nützlich. Ein erweitertes Beispiel soll die Motivation für die Indikatorfunktion weiter erhöhen.

Berechnet werden soll die (erwartete) Anzahl der Ereignisse "Kopf" bei $n$ Münzwürfen. Man kann dafür die Möglichkeiten (sprich Formeln) für Binomialverteilungen verwenden, betrachtet dabei die Wahrscheinlichkeit 0-mal Kopf, 1-mal Kopf usw. einzeln und hat einen komplizierten Rechenweg vor sich. Wesentlich einfacher ist dies mit der Indikatorfunktion. \begin{equation} X_i=I\{ \text{das Ergebnis des $i$-ten Wurfes ist Kopf}\} \end{equation} Außerdem sei die Zufallsvariable $X$ die Gesamtanzahl der Ereignisse "Kopf" bei $n$ Münzwürfen. $X$ muss also gleich der Summe aller $X_i$ von $i=1$ bis $i=n$ sein: \begin{equation} X=\sum_{i=1}^{n}X_i \end{equation} Berechnet werden soll der Erwartungswert, also \begin{equation} E[X]=E[\sum_{i=1}^{n}X_i] \end{equation}

Den Erwartungswert jedes einzelnen $X_i$ können wir berechnen, siehe obiges Lemma. Stellt sich nur noch die Frage, wie man die Summe von Erwartungswerten berechnet. Hier setzt ein Satz ein, welcher der probabilistischen Analyse mittels der Indikatorfunktion zu ihrer enormen Leistungsfähigkeit verhilft. 

$E[X+Y]=E[X]+E[Y]$

Der Erwartungswert einer Summe aus zwei Zufallsvariablen entspricht der Summe der beiden einzelnen Erwartungswerte (Linearität des Erwartungswertes). Damit sind alle Voraussetzungen geschaffen, um die (erwartete) Anzahl der Ereignisse "Kopf" bei $n$ Münzwürfen zu berechnen.

\begin{equation} E[X]=E[\sum_{i=1}^{n}X_i] \end{equation} \begin{equation} =\sum_{i=1}^{n}E[X_i] \end{equation} \begin{equation} =\sum_{i=1}^{n}\frac{1}{2} \end{equation} \begin{equation} =\frac{n}{2} \end{equation}

Zwischenstand

Wir sind in der Lage, Indikatorfunktionen für Ereignisse anzugeben und den Erwartungswert für diese Indikatorfunktion zu berechnen. Außerdem können wir für eine Folge von Zufallsversuchen den Erwartungswert für das mit der Indikatorfunktion verknüpfte Ereignis berechnen. Damit steht uns ein leistungsfähiges Werkzeug zur Verfügung, mit dem auch komplexere Probleme gelöst werden können. Ein solches soll nun betrachtet werden.

Das Bewerberproblem

Vorstellung des Problems

Stellen Sie sich vor, Sie als Hauptakteur sind der Personalchef eines Unternehmens und es wurde eine neue Stelle geschaffen. Ihre Aufgabe ist es, einen neuen Mitarbeiter einzustellen und jederzeit den am besten qualifiziertesten Mitarbeiter für diese Stelle zu beschäftigen. Hierfür beauftragen Sie eine Vermittlungsagentur, welche Ihnen täglich einen Kandidaten zu einem Vorstellungsgespräch schickt. Für das Gespräch entstehen Ihnen Kosten ($c_i$), welche Sie an die Agentur abführen müssen. Für die Einstellung eines Kandidaten fallen Ihnen jedoch deutlich höhere Kosten ($c_h$) an, da die Agentur eine Vermittlungsgebühr erhebt und Sie den vorherigen Mitarbeiter entlassen müssen. Ihr Wunsch ist es nun zu wissen, was für Kosten auf Sie zukommen, wenn Sie immer wieder den besten Kandidaten einstellen. 

Die Analyse von Kosten, egal ob von Zeit, Speicher oder z.B. entstehenden Kosten in einer Währung, unterscheiden sich nicht!

Beweis: Zur Laufzeituntersuchung betrachten wir grundlegende Operationen eines Algorithmus. Bei der Kostenbestimmung in diesem Beispiel untersuchen wir, wie oft neu eingestellt wird (also die Operation "neuen Kandidat einstellen").

Sei $m$ die Anzahl der eingestellten Kandidaten, so belaufen sich die Gesamtkosten auf $\mathcal O(n\cdot c_i+m\cdot c_h)$. Der Worstcase ist offensichtlich, jeder Kandidat muss eingestellt werden ($\mathcal O(n\cdot c_h)$), da die Kandidaten in (aufsteigend) sortierter Reihenfolge vorstellig werden. Beim Bestcase ist es gerade umgekehrt, beide Varianten sind jedoch praxisfern. Wie hier beschrieben benötigen wir Wissen über die Verteilung der Eingaben. Wir haben also eine Liste von Kandidaten, welche uns vorgestellt werden, wissen aber nicht, ob und wie diese sortiert ist. Wir ändern das Modell ein wenig ab: Die von uns beauftragte Agentur schickt eine Liste aller Kandidaten (nur die Namen) und wir bestimmen, welchen Kandidaten wir wann sprechen wollen. Das machen wir, natürlich, zufällig.

Analyse mittels der Indikatorfunktion

Da wir durch Manipulation der Eingaben die Verwendung der probabilistischen Analyse ermöglicht haben, können wir das Bewerberproblem nun mit der Indikatorfunktion analysieren. Dazu definieren wir eine Zufallsvariable $X$, welche beschreibt, wie oft ein neuer Kandidat eingestellt wird. Außerdem benötigen wir die Indikatorfunktion $X_i$ \begin{equation} X_i=I \{\text{Kandidat }i\text{ wird eingestellt}\} \end{equation} \begin{equation} =\begin{cases} 1 &\text{falls Kandidat }i\text{ eingestellt wird}\\ 0 &\text{falls Kandidat }i\text{ nicht ingestellt wird} \end{cases} \end{equation} Außerdem gilt $X=X_1 + X_2 + X_3 + \dots + X_n$. Mit der Anwendung des Lemmas aus Indikatorfunktionen erhält man \begin{equation} E[X_i]=Pr \{\text{ Kandidat }i\text{ wird eingestellt}\} \end{equation}

Es fehlt noch die Wahrscheinlichkeit dafür, das Kandidat $i$ eingestellt wird. Diese zu benennen ist nicht schwierig, achtet man auf die bisherigen Ergebnisse. So haben alle Kandidaten die gleiche Wahrscheinlichkeit, zum Vorstellungsgespräch eingeladen zu werden. Die Wahrscheinlichkeit dafür, dass Kandidat $i$ besser ist als seine Vorgänger, ist also $\frac{1}{i}$. Da immer der beste Kandidat eingestellt wird entspricht $\frac{1}{i}$ auch der Wahrscheinlichkeit für die Einstellung des Kandidaten $i$. Nun gilt \begin{equation} E[X_i]=\frac{1}{i} \end{equation} und $E[X]$ kann wie im Einführungsbeispiel zu Indikatorfunktionen berechnet werden. \begin{equation} E[X]=E[\sum_{i=1}^{n}X_i] \end{equation} \begin{equation} =\sum_{i=1}^{n}E[X_i] \end{equation} \begin{equation} =\sum_{i=1}^{n}\frac{1}{i} \end{equation} \begin{equation} =\ln n + \mathcal O(1) \end{equation} Der letzte Schritt ergibt sich aus einem Satz über harmonische Reihen, wobei für $n\in \mathcal N$ die $n$-te harmonische Zahl definiert ist durch \begin{equation} H_n=1+\frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n} \end{equation} \begin{equation} =\sum_{k=1}^{n}\frac{1}{k} \end{equation} \begin{equation} =\ln n + \mathcal O(1) \end{equation}

Es werden folglich im Durchschnitt $\ln n$ Kandidaten eingestellt, die Kosten belaufen sich auf $\mathcal O(c_h\cdot \ln n)$. Gegenüber dem Worstcase mit $\mathcal O(n\cdot c_h)$ stellt dies eine deutliche Verbesserung dar.

Verbesserung durch randomisierten Algorithmus

Wie im obigen Abschnitt deutlich geworden ist, konnten die Kosten für die Einstellungen deutlich verringert werden. Zur Erinnerung sei gesagt, das dies nur durch die Änderung des Modells möglich war, also durch die zufällige Auswahl der Kandidaten. Gewünscht ist natürlich, dass ohne Veränderung der Eingabe und damit für alle Eingaben dieses Ergebnis erzielt werden kann. Die Lösung dieses Problems ist trivial: Der erste Schritt des Algorithmus ist das zufällige Vertauschen der Eingaben. Dadurch wird vermieden, dass (nur) mit der Eingabe der Aufwand unseres Algorithmus beeinflusst wird. Es ist somit nicht möglich, eine Worstcase- (oder auch Bestcase-) Eingabe zu tätigen. Ebenfalls wird die schon genannte Eigenschaft von probabilistischen Algorithmen deutlich, wonach die Ergebnisse des Algorithmus trotz gleicher Eingabe verschieden sein können. Allein der Zufallszahlengenerator entscheidet, wie die Eingaben schließlich bearbeitet werden, im Beispiel die Kandidaten zum Vorstellungsgespräch eingeladen werden. Stellt sich abschließend nur die Frage, wie man eine Liste von Eingaben, beispielsweise die Kandidatenliste, zufällig "mischt". Eine Möglichkeit besteht darin, den Feldelementen zufällige Prioritäten zuzuordnen und dann nach diesen zu sortieren. Eine weitere Möglichkeit ist das Iterieren über die Liste und das Vertauschen des $i$-ten Listenelementes mit einem zufällig gewählten Listenelement vom $i$-ten bis zum $n$-ten Element.

Weiterführende Beispiele

Wie bei der Lösung des Bewerberproblems deutlich wurde, ist die Verbindung aus Algorithmen und Zahlentheorie äußerst leistungsfähig. Für umfangreichere beziehungsweise einige andere Beispiele sind allerdings weitreichendere mathematische Kenntnisse nötig. Diese durchaus interessanten Problemstellungen und Lösungsverfahren können hier nicht behandelt werden, sollen aber nicht unerwähnt bleiben. So kann man mittels des hier vermittelten Wissens beispielsweise folgende Problemstellungen lösen.

  • Das Geburtstagsparadoxon
  • Coupon-Sammler-Problem
  • Glückssträhnenanalyse
  • Das online-Bewerberproblem
  • Das Hutproblem


Fazit

Mit der Vorstellung der probabilistischen Analyse wurde ein Werkzeug vermittelt, welches in die Lage versetzt, Algorithmen bereits effizient zu entwerfen und die Effizienz von Algorithmen nachträglich zu verbessern. Es ist Wissen aus der Kombinatorik nötig, welches ebenfalls wiederholt wurde. Die probabilistische Analyse kann nun zur Ermittlung von Kosten eines Algorithmus herangezogen werden, wobei diese nicht zwangsläufig die Laufzeit sein müssen. Auf die nötigen Bedingungen zur Anwendung der probabilistischen Analyse wurde hingeweisen sowie mit der Verwendung von randomisierten Algorithmen eine Möglichkeit aufgezeigt, diese Bedingungen zu optimieren. Damit vereinen sich alle behandelten Kapitel und haben gemeinsam erläutert, weshalb es sinnvoll ist, sich während der Auseinandersetzung mit Algorithmen auch mit Wahrscheinlichkeiten zu beschäftigen.

Übungen

Uebungen.pdf (0.1 MB)

Literaturverzeichnis

Kontakt

Sollten während der Nacharbeitung der Vorlesung Fragen auftreten, können diese gern gestellt werden.

Dana Müller
Robert Stricker
Von „https://programmingwiki.de/AuK/Probabilistische_Algorithmen_WS13-14“
Persönliche Werkzeuge