Aus ProgrammingWiki

Inhaltsverzeichnis 1 Einführung 2 Amortisierte Laufzeitanalyse 3 Normale Warteschlangen 3.1 Benötigte Methoden 4 Binäre Heaps 4.1 Arten binärer Heaps 4.2 Grundlegende Operationen 4.2.1 Max-Heapify 4.2.1.1 Laufzeit 4.2.2 Build-Heap 4.3 Übungsaufgaben 5 Prioritätswarteschlangen 5.1 Grundoperationen 5.1.1 decrease-key(S,x,k) 5.1.2 Insert(S,x) 5.1.3 Minimum(S) 5.1.4 Extract-Min(S) 5.2 Übungsaufgaben 5.3 Adressierbare Prioritätswarteschlangen 5.3.1 Binominal Heaps 5.3.1.1 Operationen 5.3.1.1.1 merge(H1,H2) 5.3.1.1.2 remove(H,k) 5.3.1.1.3 insert(H,k) 5.3.1.1.4 extractMin(H) 5.3.1.1.5 decreaseKey(H,k,x) 5.3.1.2 Übung 5.3.2 Fibonacci-Heaps 5.3.2.1 Informatio eines Knotens 5.3.2.2 Benötigte Methoden des Heaps 5.3.2.2.1 insert 5.3.2.2.2 Min 5.3.2.2.3 extractMin 5.3.2.2.3.1 Hilfsprozedur "cleanup" 5.3.2.2.4 decreaseKey 5.3.2.2.5 remove 5.3.2.2.6 merge 5.3.2.3 Laufzeiten 5.3.2.4 Externe Links 5.3.3 Pairing-heaps 6 Laufzeiten im Vergleich

Einführung

$abc$ Eine Prioritätswarteschlange ist eine spezielle abstrakte Datenstuktur und, wie der Name bereits vermuten lässt, eine erweiterte Variante einer Warteschlange(queue). Die Elemente der Warteschlange haben Schlüssel, die ihre Priorität bestimmen. Prioritätswarteschlangen lassen sich mit verschiedenen Datenstrukturen implementieren. Hier werden sie anhand von Heaps vorgestellt.

Amortisierte Laufzeitanalyse

Eine amortisierte Laufzeitanalyse betrachtet die mittlere Laufzeit pro Operation über eine Sequenz von Operationen. Im Gegensatz zur bisher verwendeten Laufzeitanalyse wird also nicht nur der Worst Case betrachtet. Es ist möglich, dass dieser zwar eine sehr schlechte Laufzeit hat, aber nur wenige Male im Ablauf des Algorithmus vorkommt. Alle anderen Fälle können dagegen sehr günstig sein. Durch diese alternative Betrachtung kommt es oft zu einer besseren oberen Schranke für die Laufzeit.

Es gibt drei unterschiedliche Methoden:
Aggregat-Methode Zeigt, dass eine Sequenz von n (beliebigen) Operationen für alle n im worst case Zeit T(n) benötigt. Damit sind die mittleren (amortisierten) Kosten pro Operation $ \frac{T(n)}{n}$. Diese amortisierten Kosten gelten für jede Operation, auch wenn in der Sequenz verschiedene Operationstypen auftreten.

Account-Methode Verschiedenen Operationen werden verschiedene Kosten zugeordnet, diese können auch größer oder kleiner als die tatsächlichen Kosten sein. Übersteigen die amortisierten Kosten die tatsächlichen, wird die Differenz speziellen Objekten in der Datenstruktur als Kredit zugewiesen. Dieser kann später verwendet werden, wenn die tatsächlichen Kosten höher als die amortisierten sind. Dabei ist zu beachten, dass der Gesamtkredit niemals negativ sein darf.

Potenzial-Methode Verschiedenen Operationen werden verschiedene Kosten zugeordnet, diese können auch größer oder kleiner als die tatsächlichen Kosten sein. Hier wird die Differenz zwischen amortisierten und tatsächlichen Kosten der Datenstruktur als Ganzes in Form eines Potenzials zur Verfügung gestellt. Dieses wird bei Operationen benötigt, deren Kosten höher sind als die amortisierten. Eine Potentialfunktion bildet jede Datenstruktur auf eine reelle Zahl ab, die dem Potenzial entspricht. Diese Potentialfunktion ist zu Beginn immer gleich 0, danach nie negativ.

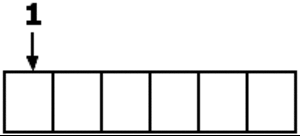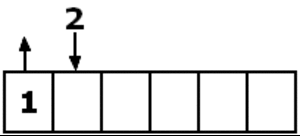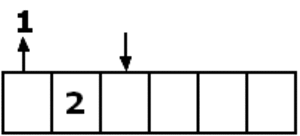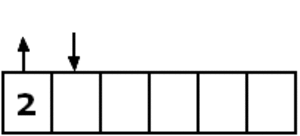
Normale Warteschlangen

Normale Warteschlangen funktionieren nach dem FiFo-Prinzip (First in, first out). Es existieren verschiedene Formen der normalen Warteschlangen, z.B. dynamisch erweiterbare oder Warteschlangen mit fester Größe.

Anwendung findet die normale Warteschlange vor allem bei verteilten Systemen bei bei der Synchronisation von Prozessen/Threads. Dies lässt sich am Beispiel der Warteschlange bei Druckaufträgen vorstellen. Wenn ein Druckauftrag gesendet wurde, der Drucker jedoch bereits in benutzung ist, so wird der Druckauftrag in eine Warteschlange gesteckt. So kann der Drucker die anstehenden Aufträge seriell abarbeiten, ohne das der Nutzer warten muss bis der Drucker wieder frei ist.

Eine gute Analogie, um die normalen Warteschlangen zu beschreiben ist "Wer zuerst kommt mahlt zuerst" (oder in unserem Beispiel "druckt zuerst").

Benötigte Methoden

Um mit normalen Warteschlangen arbeiten zu können benötigt man mindestens zwei Methoden:

• Enqueue: Zum Hinzufügen neuer Elemente.
• Dequeue: Zum Herausnehmen des "ersten" Elements.

queue= Queue(); queue.enqueue(1); queue.enqueue(2); queue.enqueue(3); queue.showElements(); System.out.println(queue.dequeue()); System.out.println(queue.dequeue()); System.out.println(queue.dequeue());

ausführen

Binäre Heaps

Ein binärer Heap kann als ein fast vollständiger binärer Baum angesehen werden. Jeder Knoten entspricht dabei einem Element des Feldes. Ist A ein Feld, dass einen Heap repräsentiert, dann hat es zwei Eigenschaften: Länge(A), die Anzahl der Elemente des Feldes, und Heap-Größe(A), die Anzahl der Elemente im Heap. Es ist also kein Element hinter A[Heap-Größe(A)] mit Heap-Größe(A) $\leq$ Länge(A) ein Element des Heaps. Die Wurzel des Baumes ist A[1]. Bei gegebenem Index i lassen sich die Indizes des Vaters Vater(i) und die des rechten und linken Kindes Right(i), bzw. Left(i) berechnen.

Vater(i)
$\lfloor$ return' i/2 $\rfloor$

Right(i)
return 2i+1

Left(i)
return 2i

Die Höhe eines Knoten ist als die Anzahl der Kanten des längsten einfachen absteigenden Pfades zu einem Blatt definiert. Die Höhe des Heaps ist die Höhe seiner Wurzel. Ein Heap mit n Elementen hat die Höhe $\theta$(lb n), da er auf einem vollständigen binären Baum basiert.

Arten binärer Heaps

Es gibt zwei Arten binärer Heaps: Max-Heaps und Min-Heaps. Beide erfüllen eine spezifische Heap-Eigenschaft. Die Max-Heap-Eigenschaft besteht darin, dass für jeden Knoten i außer der Wurzel gilt: A[Vater(i)] $\geq$ A[i], d.h. der Wert eines Knotens ist stets höchstens so groß, wie der seines Vaters. In einem Max-Heap liegt das größte Element also in der Wurzel.

Ein Min-Heap ist entgegengesetzt aufgabaut. Hier gilt:

A[Vater(i)] $\leq$ A[i]. Hier liegt in der Wurzel das kleinste Element.

Für Heapsort werden Max-Heaps verwendet, für Prioritätswarteschlangen Min-Heaps.

Grundlegende Operationen

Max-Heapify

Sorgt für die Aufrechterhaltung der Heap-Eigenschaft. Erhält ein Feld A und einen Index i. Es wird angenommen, dass die Bäume, die von Left(i) und Right(i) ausgehen die Max-Heap-Eigenschaft erfüllen, A[i] dagegen kann kleiner als seine Kinder sein, was die Heap-Eigenschaft verletzen würde. Max-Heapify lässt den Wert von A[i] im Heap nach unten sinken, sodass der von i ausgehende Teilbaum zu einem Max-Heap wird.

Max-Heapify(A,i)
l$\leftarrow$Left(i)
r$\leftarrow$Right(i)
if l $\leq$ heap-größe[A] und A[l] > A[i]
  then maximum $\leftarrow$ l
  else maximum $\leftarrow$ i
if r $\leq$ heap-größe[A] und A[r] > A[maximum]
  then maximum $\leftarrow$r
if maximum $\neq$ i
  then vertausche A[i] $\leftrightarrow$ A[maximum]
       Max-Heapify(A,maximum)

heapO = Heap(); int[] heap = {1,5,3,2,4}; heapO.maxHeapify(heap, 0); heapO.print(heap);

ausführen

Laufzeit

Die Laufzeit setzt sich zusammen aus $\Theta(1)$ um die Beziehungen zwischen A[i], A[Left(i)] und A[Right(i)] zu bestimmen, sowie der Zeit für die Ausführung von Max-Heapify auf einen von i ausgehenden Teilbaum. Die von den Kindern ausgehenden Teilbäume haben höchstens die Größe $\frac{2n}{3}$. Der schlechteste Fall tritt ein, wenn die letzte Ebene des Baumes exakt halb gefüllt ist. Die Rekursionsgleichung $T(n) \leq T(\frac{2n}{3})+\Theta(1)$ beschreibt die Laufzeit von Max-Heapify. Nach dem Mastertheorem ist die Lösung $T(n)=O(lg (n))$. Die Laufzeit auf einen Knoten der Höhe h kann auch mit $O(h)$ angegeben werden.

Build-Heap

Um ein Feld A[1..n] mit n=länge[A] in einen Max-Heap zu überführen kann die Prozedur Max-Heapify bottom-up angewendet werden. Alle Elemente im Teilfeld A[($\lfloor$ $\frac{n}{2}$ $\rfloor +1$)..n] sind Blätter des Baumes, daher sind sie zu Beginn einelementige Heaps. Build-Max-Heap durchläuft alle übrigen Knoten und führt dort Max-Heapify aus.

Build-Max-Heap(A)
heap-größe[A] $\leftarrow$ länge[A]
for i $\leftarrow \lfloor$länge[A]/2$ \rfloor $ downto 1
   do Max-Heapify(A,i)

heapO = Heap(); int[] heap = {1,2,3,5,4,7,8,9}; heapO.buildMaxHeap(heap); heapO.print(heap);

ausführen

Eine obere Schranke für die Laufzeit von Build-Max-Heap lässt sich grob abschätzen. Max-Heapify kostet Zeit O(lg n) und wird O(n) mal aufgerufen. Die dadruch abgeschätzte Schranke O(n lg n) ist allerdings nicht sehr genau. Um eine schärfere Schranke herzuleiten nutzt man aus, dass die Laufzeit von Max-Heapify mit der Höhe des Knotens variiert und dass die Höhe meißtens klein ist. Ein n-elementiger Heap hat die Höhe $ \lfloor lg n \rfloor $ und es gibt höchstens $\lceil n/2^{h+1} \rceil $ Knoten mit Höhe h. Da die Zeit von Max-Heapify auf einen Knoten der Höhe h O(h) ist, kann für Build-Max-Heap die obere Schranke $\sum\limits_{h=0}^{\lfloor lg n \rfloor} \lceil \frac{n}{2^{h+1}}\rceil O(h) = O (n \sum\limits_{h=0}^{\lfloor lg n \rfloor} \frac{h}{2^{h}} $ angegeben werden. Sei x=1/2, dann ist $\sum\limits_{h=0}^{\infty}\frac{h}{2^{h}} = \frac{1/2}{(1-1/2)^{2}} =2$

Damit kann man die Laufzeit durch $O (n \sum\limits_{h=0}^{\lfloor lg n \rfloor} \frac{h}{2^{h}} = O(\sum\limits_{h=0}^{\infty}\frac{h}{2^{h}} = \frac{1/2}{(1-1/2)^{2}}) =O(n)$ abschätzen.

Übungsaufgaben

• Mastertheorem Anwendung für die Rekursionsgleichung von Max-Heapify ($T(n) \leq T(\frac{2n}{3})+\Theta(1)$)

Allgemeine Form des Mastertheorems:
$T(n) = a \cdot T(\textstyle \frac{n}{b}) + f(n)$

• Was ist die maximale und minimale Anzahl von Elementen in einem (Binären) Heap der Höhe h?

• In einem max heap, wo befindet sich das kleinste element, wenn alle paarweise verschieden sind?

• Ist [5,4,1,3,2] ein max heap?

• Was macht Max-Heapify(A,i), wenn A[i] größer als seine Kinder ist

Prioritätswarteschlangen

Wie bei Heaps gibt es auch hier zwei Varianten Max-Prioritätswarteschlangen und Min-Prioritätswarteschlangen. Im Folgenden werden Min-Prioritätswarteschlangen verwendet.

Prioritätswarteschlange

Eine Prioritätswarteschlange ist eine Datenstruktur für die Speicherung einer Menge S, deren Elementen jeweils ein Wert zugeordnet ist, den man als Schlüssel bezeichnet.

Grundoperationen

decrease-key(S,x,k)

Verringert den Wert des Schlüssels von Element x auf den neuen Wert k. Da so die Heap-Eigenschaft verletzt werden kann, dürchläuft die Prozedur anschließend vom Knoten i beginnend den Heap bis zur Wurzel um die richtige Position zu finden.

decrease-key(S,i,k)
if k > A[i]
then return "neuer Schlüssel ist größer als der aktuelle Schlüssel"
A[i]$\leftarrow$k
while i > 1 und A[Vater(i)] > A[i]
    do A[i]$\leftrightarrow$A[Vater(i)]
      i$\leftarrow$Vater(i)

Laufzeit auf einem Heap mit n Elementen ist $O(lg$ $n)$, da der Pfad vom Knoten i bis zur Wurzel die Länge $O(lg$ $ n)$ hat.

Insert(S,x)

Fügt das Element x in die Menge S ein. Die Operation kann als S $\leftarrow$ S $\bigcup$ {x} geschrieben werden. Zunächst wird der Heap erweitert, indem ein neues Blatt mit dem Platzhalter Schlüssel "X" eingefügt wird. Anschließend wird mittels Heap-Decrease-Key der korrekte Schlüssel eingefügt und gegebenenfalls die Heap-Eigenschaft wiederhergestellt,

Insert(S,x)
heap-größe[A]$\leftarrow$heap-größe[A]+1
A[heap-größe[A]]$\leftarrow$X
Heap-Decrease-Key(A,heap-größe[A],x)

Laufzeit auf einem Heap mit n Elementen ist $O(lg$ $ n)$.

Minimum(S)

gibt das Element mit dem kleinsten Schlüssel zurück

Minimum(s)
return A[1]

Laufzeit trivial $\theta(1)$.

Extract-Min(S)

entfernt das kleinste Element und gibt es zurück

Extract-Min(S)
if heap-größe[S]<1
  then return "Heap Unterlauf"
min$\leftarrow$S[1]
S[1]$\leftarrow$S[heap-größe(S)]
heap-größe(S)$\leftarrow$heap-größe(S)-1
Min-Heapify(S,1)
return min

Die Laufzeit von Extract-Min(S) ist $O(lg$ $ n)$, da zusätzlich zu Min-Heapify nur eine konstante Zeit kommt.

Übungsaufgaben

• Insert(H,2) H=[3,4,5,6,7,8,9]

• Extract-Min([H'])

Adressierbare Prioritätswarteschlangen

Die Struktur binärer Heaps ist zu unflexibel für die Implementierung adressierbarer Prioritätswarteschlangen, daher werden hierfür andere Formen von Heaps verwendet. Diese versprechen schnellere Laufzeiten für insert, decreaseKey, remove und merge. Durch diese Operationen können sehr schlecht struktuierte bäume entstehen, daher werden bei einigen Varianten zusätzliche rebalancing Methoden verwendet. Der Einzelne binäre Baum wird ersetzt durch eine Sammlung von Bäumen (einem sogenannten Wald) mit willkürlicher Struktur. Dabei erfüllen die einzelnen Bäume natürlich immernoch die Heap-Eigenschaft. Weiterhin wird ein Zeiger auf jedes Heap Element im Speicher behalten. Dabei zeigt minPtr auf das kleinste Element. Der Wald wird mit drei Operationen verwaltet: Einen neuen Baum hinzufügen, zwei Bäume verbinden und einen Teilbaum abschneiden.

Binominal Heaps

Im Gegensatz zu Binären-Heaps können Binomial-Heaps effizient vereinigt werden. Alle Operationen lassen sich mit einer Worst-Case-Laufzeit von O(log n) implementieren. Die Bäume eines Binomial-Heaps sind rekursiv definiert.

• Ein Binomial-Baum der Ordnung 0 besteht aus einem einzelnen Knoten.
• Ein Binomial-Baum der Ordnung k besitzt eine Wurzel mit Grad k deren Kinder genau die Ordnung k-1, k-2, ..., 0 (in dieser Reihenfolge) besitzen.

Damit lässt sich ein Binomial-Baum der Ordnung k leicht aus zwei Binomial-Bäumen der Ordnung k-1 erstellen. Dabei wird einer der beiden Bäume zum am weitesten links stehenden Kind des anderen gemacht. Daraus lässt sich ableiten, dass ein Binomial-Baum der Ordnung k genau $2^{k}$ Knoten und Höhe k hat.

Operationen

merge(H1,H2)

Die Verschmelzung zweier Heaps ist die zentrale Operation bei binomial-Heaps, da sie bei allen anderen Operationen aufgerufen wird. Dazu werden simultan die Listen der beiden Heaps beginnend bei den Bäumen niedrigster Ordnung durchlaufen. In einer speziellen Variablen wird – ähnlich der bitweisen Addition – ggf. ein Übertrag (in Form eines Baumes) festgehalten. Anfangs ist dieser Übertrag leer. Sei x die höchste Binärstelle von $n_{1}+n_{2}$ ungleich 0, das heißt $x=log_{2}(n_{1}+n_{2}+1)-1$. Zu jeder natürlichen Zahl k mit $0\leq k\leq x$ wird nun in aufsteigender Reihenfolge die Anzahl der Bäume mit Ordnung k in beiden Heaps und in der Übertragsvariablen betrachtet.
Anzahl der Bäume mit Ordnung k:

• = 0 es passiert nichts.
• = 1 der entsprechende Baum wird in den neuen Heap übernommen und der Übertrag geleert.
• = 2 der Baum mit dem größeren Schlüssel in der Wurzel wird zum am weitesten links stehenden Kind des anderen Baumes gemacht. Der entstehende Baum mit Ordnung k+1 wird als Übertrag behalten.
• = 3 der Baum aus dem Übertrag wird in den neuen Heap übernommen und von den beiden Bäumen in den Heaps wird der Baum mit dem größeren Schlüssel in der Wurzel zum am weitesten links stehenden Kind des anderen Baumes. Der entstehende Baum mit Ordnung k+1 wird als Übertrag behalten.

Jeder dieser Schritte lässt sich in konstanter Zeit durchführen. merge(H1,H2) benötigt maximal logarithmische Zeit, da maximal $\log_2(n_1+n_2+1)$ derartige Schritte getätigt werden.

remove(H,k)

Der Wert von k wird mittels decreaseKey zum kleinsten Element im Heap gemacht und anschließend mit extractMin(H) gelöscht.

insert(H,k)

Erzeugt einen neuen Heap, der nur k enthält. Dieser wird mit merge(H,k) mit dem Heap verbunden. Durch merge ist die Laufzeit O(log n). Die amortisierte Laufzeit ist O(1).

extractMin(H)

Die kleinste Wurzel wird gesucht und mit remove(H,min) entfernt und zurückgegeben. Die dadurch entstehenden Teilbäume werden zu einem neuen Heap H'. Dieser wird mit merge(H,H'). Da jeder Baum maximal log n Kinder hat, benötigt das Anlegen des neuen Heaps eine Zeit von O(log n). Das Zusammenfügen geschieht ebenfalls in Zeit O(log n). Die Laufzeit für extractMin(H) ist damit O(log n).

decreaseKey(H,k,x)

Der Schlüssel k wird zunächst entfernt und anschließend mit dem neuen Wert x wieder eingefügt. Die Laufzeit ist O(log n), da ein binomial Baum die maximale Höhe log n hat.

Übung

Laufzeit von remove?

Fibonacci-Heaps

Ein Fibonacci-Heap besteht aus einer Liste von Bäumen mit geordneten Nachfolgern, deren Knoten Schlüssel und möglicherweise eine Markierung enthalten.
Der Schlüssel wird hierbei als Priorität gesehen. Wie bei allen anderen Heaps muss die Heap-Eigenschaft vorhanden sein.

Ein Fibonacci-Heap wird normalisiert genannt, wenn alle Bäume unterschiedliche Wurzelränge (Prioritäten) haben.

Informatio eines Knotens

In einem Fibonacci-Heap hat jeder Knoten Folgende Informationen:

• wer ein Kind ist (Zeiger auf eins und nur eins seiner Kinder)
• wer sein rechter Nachbar ist
• wer sein linker Nachbar ist
• wer sein Vater ist
• der Key
• der Grad
• ob er markiert ist

Somit erhält man die Struktur von zirkuläre, doppelverkettete Listen

• Vorteile:
  • Entfernen eines Elementes in konstanter Zeit
  • Vereinigen zweier Listen in konstanter Zeit

Benötigte Methoden des Heaps

Fibonacci-Heaps unterstützen die Operationen:

• insert: Einfügen eines Elementes.
• remove: Entfernen eines Elemente.
• Min: Finden des Elements mit dem minimalen Schlüssel.
• extractMin: Rückgabe und Entfernen eines Elementes mit minimalem Schlüssel (In einem Min-Heap entspricht dies der höchsten Priorität).
• decreaseKey: Verringern des Schlüssels eines Elementes.
• merge: Verschmelzen zweier Bäume.

insert

Um ein Element hinzuzufügen wird ein neuen 1-Elementiger Baum erstellt. Sollte der Key kleiner als der aktuell minimalste Key sein. So wird der entsprechende Zeiger neu gesetzt.
Da keine weiteren Operationen notwendig sind beträgt die Laufzeit $O(1)$

Min

Liefert den Eintrag mit minimalem Schlüssel. Da jederzeit ein Zeiger auf den minimalen Knoten vorhanden ist beträgt die Laufzeit $O(1)$

extractMin

Liefert den Eintrag mit minimalem Schlüssel und entfernt diesen Knoten.
Die Kinder des Knotens werden als neue Bäume hinzugefügt.

• Problem:
  • Der Heap würde so extrem schnell in die Breite wachsen und die Prozedur zum Bestimmen des minimalen Knotens würde sehr schnell lineare Zeit benötigen.

• Lösung
  • Neue (private) Prozedur cleanup um den Heap aufzuräumen. Erst dann wird das neue Minimum bestimmt.

Hilfsprozedur "cleanup"

Diese Prozedur soll verhindern, dass der Heap unnötig in die Breite geht.
Zuerst wird ein Array $A$ von $0$ bis $2log(n)$ initialisiert. ($n$ = Anzahl der Knoten)
In diesem soll nach dem cleanup an Stelle $d$ ein Zeiger auf einen Baum stehen,

Es werden also alle Elemente der Wurzelliste in dieses Array eingeordnet. Kommt es dabei zu einer Überschneidung (zwei Elemente haben den gleichen Grad), so wird das Element mit dem kleineren Schlüssel zum
Vater des anderen gemacht, der Grad desselben wird erhöht und es wird in das Array einsortiert.
Die obige mathematische Analyse versichert, dass höchstens $2log(n)$ Elemente im Array stehen.
Schließlich muss die neue Wurzelliste aufgebaut werden. Dazu werden alle Elemente des Arrays A durchgegangen und mithilfe von merge wieder zu einem Heap zusammengebaut.

Danach kann der minimale Knoten bestimmt werden.

decreaseKey

Für diese Operation sind folgene Schritte und Fallunterscheidungen notwendig:

Schritt 1

• Den Key des gewünschten Knotens veringern
  • Fall 1: Heap-Ordnung NICHT verletzt
    • Man ist fertig
  • Fall 2: Heap-Ordnung wurde verletzt
    • Schritt 1.1
    • Knoten + alle Kinder auf die oberste Ebene setzten und eine Marke (falls vorhanden) entfernen
    • Schritt 1.2
    • Vater des Knotens markieren
      • Fall 1: Vater war nicht markiert
        • Man ist ferig
      • Fall 2: Vater war bereits markiert
        • Schritt 1.3
        • Alle Schritte ab Schritt 1.1 wiederholen

remove

Um einen Knoten zu entfernen wird die Methode decreaseKey auf den Knoten angewendet, der Key wird dabei um $-\infty$ veringert.
Anschließend wird die Methode deleteMin auf den heap angewendet.

Die kombinierte Laufzeit dieser beiden Methoden ist also die Laufzeit dieser Methode.
$O(log(n)+1) = O(log(n))$

merge

Da es sich um Doppelt-Verkettete Listen handelt können die beiden zu mergenden Heaps an jeweils einer Stelle aufgebrochen und verlonkt werden.
Anschließend werden die beiden minimal-Knoten verglichen. Der Zeiger auf den kleineren Knoten "überlebt". Infolge dessen ist die Laufzeit $O(1)$.

Laufzeiten

Operation	Laufzeit
insert	$O(1)$
remove	$O(log(n))$*
Min	$O(1)$
extractMin	$O(log(n))$*
decreaseKey	$O(1)$*
merge	$O(1)$

(*)Amortisierte Kosten. Worst-Case ist $O(n)$

Externe Links

• Simulation eines Fibonacci-Heaps (Java-Applet)
• Pseudo-Code für Fibonacci-Heaps (Einige Methoden sind anders benannt)

Pairing-heaps

Fibonacci Heaps haben zwei Schwächen. Ihre Implementierung ist sehr kompliziert und sie haben sich in der Praxis als weniger effizient erwiesen, als theoretisch schwächere Formen von Heaps. Dies ist darauf zurückzuführen, dass sie in der einfachsten Variante Speicher für vier Zeiger pro Knoten benötigen. Im Vergleich dazu werden sonst nur zwei bis drei Zeiger verwendet. Pairing-Heaps wurden entwickelt um Fibonacci-Heaps in Theorie und Praxis zu schlagen. Eine komplette Analyse ist sehr schwierig und bisher nicht erfolgt. Bei Pairing-Heaps handelt sich um eine selbstverwaltende Variante der binomialen Heaps. Es wird angenommen, dass sie theoretisch genauso Effizient sind, wie Fibonacci Heaps. Die beste Analyse im Orginalpaper liefert eine Zeit von $O(lg$ $ n)$ für jede Heap Operation.

Die wichtigste Operation ist delete-min, da nur hier die Heapsturktur gewartet wird. Die anderen Operationen(make-heap, extract-min, delete, insert, meld, decreaseKey) sind wie bereits bekannt implementiert. Die zugrunde liegende Datensturktur ist ein Binärbaum. Jeder Knoten hat einen linken Zeiger, der auf das erste Kind zeigt und einen rechten Zeiger, der auf den nächstgrößeren Knoten zeigt. Damit decreaseKey und delete effizient sind wird noch ein dritter Zeiger benötigt, der auf den Vaterknoten zeigt. Dieser Zeiger kann eingespart werden, indem man einen Zeiger auf das linke Kind und einen auf den rechten Geschwisterknoten, bzw. den Elternknoten richtet. Dies geschieht auf Kosten einen konstanten Faktors in der Laufzeit.

Die Operationen make-heap, find-min, insert, meld und drecreaseKey haben eine Laufzeit von $O(1)$ worst case. Zum Löschen eines Elements mittels delete wird $O(1)$ und die Zeit für eine delete-min Operation benötigt. Damit sind delete und delete-min sind die einzigen Operationen, die in nicht konstanter Zeit laufen.

delete-min(H)

Durch das Löschen der Wurzel ensteht eine Gruppe von Heaps. Diese müssen nun zu einem neuen Heap zusammengefügt werden. Es hat sich gezeigt, dass die Reihenfolge hierbei eine Rolle spielt. Wie man die Kombination auch gestaltet, die Grenze für den worst case ist $\theta(n)$, da jeder n-knotige Baum, dessen Wurzel n-1 Kinder hat durch eine Reihe von $O(n)$ make-heap, insert und meld Operationen aufgebaut werden kann.

Es ist möglich eine amortisierte Laufzeit von $O(lg$ $ n)$ festzulegen. Die primitive Variante wäre, einen Baum auszuwählen und die anderen einen nach dem anderen mit ihm zu verbinden. Dies liefert eine Laufzeit von $\theta(n)$.

Es existiert jedoch auch eine schnellere Variante. Im ersten Durchlauf werden die Bäume zu Paaren verbunden. Im zweiten werden die entstandenen Paare mit einem ausgewählten Baum verbunden. Sind die Paare beim ersten Durchlauf schlecht gewählt, so ist $\theta(\sqrt{n})$ amortisierte Zeit möglich. Damit ist diese Version schneller als die primitive.

Laufzeiten im Vergleich

Operation	Binärer Heap	Binomial Heap	Fibonacci Heap	Pairing
	worst-case	worst-case	amortisiert	amortisiert
extract-min	$\mathcal{O}(\log n)$	$\mathcal{O}(\log n)$	$\mathcal{O}(\log n)$	$\mathcal{O}(\log n)$
remove	$\mathcal{O}(\log n)$	$\mathcal{O}(\log n)$	$\mathcal{O}(\log n)$	$\mathcal{O}(\log n)$
insert	$\mathcal{O}(\log n)$	$\mathcal{O}(\log n)$	$\mathcal{O}(1)$	$\mathcal{O}(\log n)$ ($\mathcal{O}(1)$ vermutet)
decrease-key	$\mathcal{O}(\log n)$	$\mathcal{O}(\log n)$	$\mathcal{O}(1)$	$\mathcal{O}(\log n)$ ($\mathcal{O}(1)$ vermutet)
merge	$\mathcal{O}(n)$	$\mathcal{O}(\log n)$	$\mathcal{O}(1)$	$\mathcal{O}(\log n)$ ($\mathcal{O}(1)$ vermutet)