P-NP-Problem WS13-14
Aus ProgrammingWiki
Inhaltsverzeichnis |
Einleitung
In diesem Abschnitt, möchten wir das P-NP-Problem näher betrachten.
Vielmehr handelt es sich dabei um spezielle Gruppen von Problemen, von denen manche einfacher und andere schwieriger zu lösen sind. Es gibt Optimierungsprobleme, wie etwa das bereits behandelte Problem des Handelsreisenden. Dieser Art von Problemen kann man auch ein Entscheidungsproblem anhängen.
In diesem Fall wäre die Frage: "Gibt es einen Weg $k$, der kürzer ist als das vom Optimierungsalgorithmus errechnete Ergebnis?"
Aus den vorangegangenen Vorlesungen wissen wir, dass es viele unterschiedliche Probleme gibt und dass sich manche mit
polynomialen Aufwand lösen lassen und andere nicht.
An dieser Stelle folgt eine kurze Wiederholung des Polynom-Begriffs: Ein Polynom ist eine endliche Summe von Potenzen mit ganzzahligen Exponenten.
\[\sum_{i=0}^n a_ix^i = a_0 + a_1x + a_2x^2 +...+ a_nx^n, n\geq0\]
Die Klassen P und NP
Das P-Problem
Diese Art von Problemen lassen sich leichter lösen, als solche der Klasse der NP-Probleme.
Die Definition lautet:
P ist die Klasse aller Probleme, die sich mit deterministischen Algorithmen in polynomialer Zeit lösen lassen.
Allgemein sagt man auch, dass es die Klasse der "praktisch lösbaren" Probleme ist.
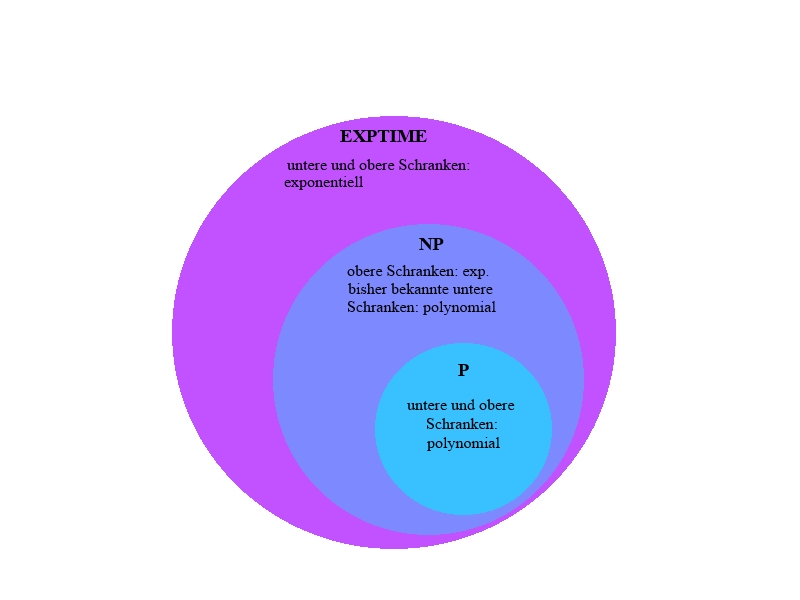
Im schlechtesten Fall, oder worst case, würde ein Algorithmus für ein P-Problem der Länge $n$ eine polynomiale Zeit mit $n$-Summanden brauchen. Somit ist der Aufwand nach oben beschränkt.
Außerdem existieren Probleme, die zwar berechenbar sind, aber dennoch nicht in P liegen.
Um diese Probleme zu lösen ist ein exponentieller Mindestaufwand vonnöten. Sie werden EXPTIME genannt. Demzufolge gilt P $\subset$ EXPTIME.
Das NP-Problem
Neben den effizient zu lösenden Problematiken gibt es noch viele weitere von denen bisher (noch) nicht bekannt ist, ob es einen Algorithmus gibt, der mit polynomialen Aufwand arbeitet. Diese Klasse nennt man NP-Probleme.
Um sie näher zu beschreiben, nehmen wir den Nichtdeterminismus als theoretisches Konzept zur Hilfestellung hinzu. Aus der Theoretischen Informatik ist bekannt, dass nichtdeterministische endliche Automaten äquivalent zu deterministischen arbeiten. Ebenso ist es bei den TURING-Maschinen.
Die Definition lautet:
NP-Probleme sind diejenigen, die mit nichtdeterministischen Algorithmen in Polynomialzeit gelöst werden können.
Bisher sind einige untere Schranken für NP-Probleme bekannt. Sie sind teilweise linear oder quadratisch. Für obere Schranken werden exponentielle (manchmal auch mehrfach exponentielle) Aufwände angegeben.
Es ist erwiesen, dass P $\subseteq$ NP gilt, aber ob auch P=NP gilt, konnte bis heute weder bewiesen noch wiederlegt werden.
NP-Vollständigkeit
Polynomiale Reduktion
NP-schwere Probleme
NP-vollständige Probleme
Nachweis der NP-Vollständigkeit eines Problems
Satz von Steven A. Cook
"Das Erfüllbarkeitsproblem der Aussagenlogik (SAT) ist NP-vollständig."
COOK fand 1971 eine Teilmenge von NP, auf die sich alle NP-Probleme reduzieren lassen. Diese Klasse nennt man NP-vollständig.
Das SAT-Problem (satisfiability-problem) lässt sich wie folgt beschreiben:
"Gibt es eine Belegung von booleschen Variablen $x_i$ mit je einem Wert aus $\left\{t,f\right\}$, sodass ein gegebener Ausdruck wahr wird?"
Zum Beispiel ($x_1$ $\vee$ $x_2$ $\vee$ $x_3$) $\land$ ($\neg$ $x_4$ $\vee$ $x_2$ $\neg$ $x_1$).
An diesem Beispiel kann man sehen, dass eine deterministische Lösung alle Möglichkeiten berechnen würde.
Der Aufwand entspräche $2^4$.
Nimmt man stattdessen die Dienste der "Guten Fee" (Nichtdeterminismus) in Anspruch, erhält man einen polynomialen Aufwand.
Das Ramsey-Problem
Wenn jemand eine Party gibt, könnte er sich fragen, wie viele Gäste er mindestens einladen muss, damit sich entweder $m$ Personen kennen, oder $n$ Personen nicht kennen.
Genau diese Fragestellung beschreibt das RAMSEY-Problem, auch Party-Problem genannt.
Um den Sachverhalt zu verdeutlichen, geben wir einen stets vollständigen Graphen an. Die Knoten stehen für die einzelne Person und die Kanten geben Auskunft über die Beziehungen zwischen den Personen.
Außerdem wählen wir die Farbe blau für: "sich kennen" und rot für: "sich nicht kennen" und tragen so alle Kanten in dem Graphen ein.
Entsteht auf diese Weise ein Teilgraph, der nur aus blauen bzw. roten Kanten besteht, nennt man ihn eine Clique.
Man kann nach Cliquen suchen, obgleich nicht in jedem Graphen welche zu finden sind. Diese Suche ist Gegenstand
des Cliquenproblems. Es wird untersucht, ob es in einem Graphen $G$ und einer Zahl $n$ eine Clique der Größe $n$ gibt.
Das heißt, dass es mindestens $n$ Knoten geben muss, die alle untereinander verbunden sind.
Vorteile praktischer Unlösbarkeit
Nun kann aber die Unlösbarkeit bestimmter Probleme auch zu unserem Vorteil genutzt werden. Sie findet Anwendung in der Kryptographie, die sich mit Methoden der Geheimhaltung von Daten beschäftigt. Dabei ist die Kryptologie eng mit der Kryptographie verbunden. Sie stellt die Wissenschaft von den (offenen) Geheimschriften dar und bildet mit Hilfe der Kryptoanalyse Vorschriften zur Entzifferung von Code.
In der Praxis greift man auf Ver- und Entschlüsselungsverfahren zurück, die nicht oder nur sehr schwer lösbar sind.
Zur Verschlüsselung wird ein Schlüssel benötigt, der die zu übertragenden Daten codiert. Dieser Schlüssel muss dem Empfänger zur Verfügung gestellt werden, damit die codierten Daten wieder entschlüsselt werden können. Hierbei kann es allerdings zu Schwierigkeiten kommen: erfolgt die Übertragung des Schlüssels unverschlüsselt, kann von außen unbefugt auf gesendete Daten zugegriffen werden, was dem Ziel der Verschlüsselung widerspricht. Zudem können die abgefangenen Informationen manipuliert werden, ohne dass der Empfänger von der potenziellen Gefahr weiß. Wird der Schlüssel allerdings verschlüsselt übertragen, kann keine Decodierung der Daten vorgenommen werden, da der Schlüssel für den Empfänger nicht lesbar ist.
Um dieses Problem bei der Übertragung des Schlüssels zu umgehen, kann man einen öffentlichen Schlüssel verwenden, der zum Beispiel beim RSA-Verfahren zum Einsatz kommt.
RSA-Verfahren
Das RSA-Verfahren ist das erste Public-Key-Kryptosystem und wurde 1977 von Rivest, Shamir und Adleman erfunden.
Der öffentliche Schlüssel $C$ besteht aus den zwei Teilen $m$ und $e$ und wird zur Verschlüsselung einer Nachricht benutzt. Unter Verwendung des privaten Schlüssels $D$, welcher $m$ und den geheimen Teil $d$ enthält, kann die Nachricht dechiffriert werden.
Schlüsselerzeugung
Wir bestimmen $m$, indem wir zwei möglichst große Primzahlen $p$ und $q$ wählen und diese miteinander multiplizieren, d.h. $m=p \cdot q$. Die Primzahlen sollten mehr als 200 Stellen haben. Danach ermitteln wir $\varphi(m)$, welches die Anzahl der Zahlen von $1,...,m-1$, die zu $m$ teilerfremd sind, angibt.
Dabei gilt für Primzahlen $p$$\neq$$q$: $\varphi(p \cdot q)=(p-1)\cdot(q-1)$.
Desweiteren wählen wir eine zufällige Zahl $e$, sodass $ggT(\varphi(m),e)=1$ eintritt. Dadurch können wir den geheimen Teil $d=e^{-1} \bmod \varphi(m)$ berechnen.
Beispiel
$p=17$ $q=19$
$m=p \cdot q=17 \cdot 19=323$
$\varphi(m)=(p-1)\cdot(q-1)=16 \cdot 18=288$
zufällig: $e=5$
$d=e^{-1} \bmod \varphi(m)=5^{-1} \bmod 288=173$
öffentlich: (323,5) geheim: (323,173)
- Bemerkung: Der geheime Teil $d$ kann mit Hilfe des Euklidischen Verfahrens berechnet werden.
Für die Codierung bzw. Decodierung benutzen wir folgende Vorschriften:
- Verschlüsselung: $x \longmapsto x^{e} \bmod m$
- Entschlüsselung: $y \longmapsto y^{d} \bmod m$
Analog zu unserem Beispiel wählen wir für den zu verschlüsselnden Klartext den Wert $x=13$.
$y=13^{5} \bmod 323=166$
$x=166^{173} \bmod 323=13$
Fazit
Es gelingt uns nur $d$ zu berechnen, wenn uns $m$ bekannt ist. Folglich müssen wir die Primzahlen $p$ und $q$ kennen, denn $m=p \cdot q$. Diese sind allerdings aufgrund ihrer Größe nur mit exponentiellem Aufwand bestimmbar.
Der Vorteil des RSA-Verfahrens liegt also in der Faktorisierung von $m$, für die es bisher keinen effizienten Algorithmus gibt, und die Lösung einer Verschlüsselung praktisch unlösbar macht.
Schlussfolgerungen
Zusammenfassend lässt sich sagen, dass das P-NP-Problem eine der großen offenen Fragen der Informatik darstellt. Sollte es jemandem gelingen ein NP-vollständiges Problem mit einem Algorithmus in Polynomzeit zu lösen, würde diese Entdeckung die Welt der Algorithmen und Komplexität für immer verändern. Da es noch keine absolute Gewissheit darüber gibt, ob ein solcher Algorithmus existiert, kann man nur gespannt die Forschung verfolgen oder selber mit einsteigen.
Übungen
 | Aufgaben_P-NP-Problem.pdf (0.1 MB) |
Literaturverzeichnis
- Wagenknecht, Christian: Algorithmen und Komplexität, Fachbuchverlag Leipzig, 2003
- Cormen, Thomas; Leiserson, Charles; Rivest, Ronald; Stein, Clifford: Algorithmen, eine Einführung,Oldenbourg Verlag, 2007