Näherungsverfahren 2 WS13-14
Aus ProgrammingWiki
- Autoren
- Alexander Häse
- Dominik Bitterlich
Inhaltsverzeichnis |
DNA-Computing
Motivation
NP-Probleme lassen sich mit konventionellen Rechnern nur mit einem exponentiellen Aufwand lösen, da diese verschiedenste Rechenschritte hintereinander, das heißt seriell, verarbeiten. Ein anderer Ansatz für diese Art von Problemen stellt das DNA-Computing dar. Hierbei werden in einem Reagenzglas Informationen in DNA-Molekülen codiert. Das Reagenzglas wird somit zu einem Computer mit zahlreichen parallelen Prozessoren. Obwohl die Schaltzeit von Neuronen (Nervenzellen) im Bereich von einer Millisekunde derjenigen von Mikroprozessoren unterlegen ist, kann in der Natur zum Beispiel ein potentielles Beutetier einen Angreifer blitzartig erkennen und entsprechend reagieren. Dies ist eine Fähigkeit, welche das Vermögen von Mikroprozessoren übersteigt und die erst durch Parallelarbeit ermöglicht wird.
Biologische Grundlagen
Die gesamte Erbinformation lebender Zellen und Organismen ist in der DNA enthalten. Sie steuert in jeder einzelnen Zelle eines Lebewesens die biologischen Vorgänge wie zum Beispiel den Stoffwechsel und die Zellteilung. Alle Zellen eines Lebewesens enthalten die gleichen Erbinformationen in ihren Zellkernen. Die DNA speichert enorme Mengen an Information und wird über Generationen hinweg weitergegeben. Dadurch wird der Bestand einer Art gesichert. Der chemische Aufbau und die molekulare Struktur der DNA sind in allen Lebewesen identisch, gleichgültig ob es sich um Mensch, Pflanze, Pilz oder Bakterium handelt.
Aufbau
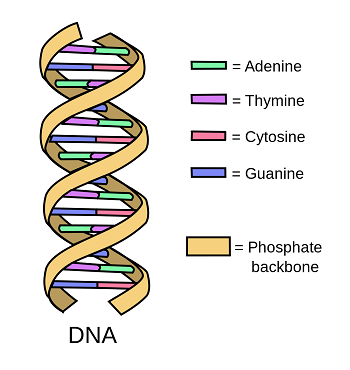
DNA kommt in allen Lebewesen vor, trägt deren Erbinformation und stellt somit den Bauplan für sämtliche Proteine eines Organismus dar. Die DNA kodiert Aminosäuresequenzen der Proteine. DNA besteht aus zwei Strängen welche umeinander gewunden sind, die sogenannte Doppelhelix. Jeder Strang besteht aus Desoxyribonucleotiden, welche über Phosphodidesterbindungen miteinander verbunden sind. Desoxyribonucleotid enthält eine organische Base, den Zucker Desoxyribose und Phosphatsäurerest. Durch die lineare Anordnung der Nucleotide entsteht ein Zucker – Phosphat Rückgrat, bekannt als Backbone, von welchem die organischen Basen, A – Adenin , T – Thymin , G – Guanin und C – Cytosin, abstehen. Durch den parallelen Verlauf stehen sich immer zwei Basenpaare gegenüber, dazwischen befinden sich Wasserstoffbrückenbindungen. Mögliche Paare sind A und T, T und A, G und C, C und G, welche als komplementären Basen bezeichnet werden. Bildlich kann man sich die Doppelhelix als Strickleiter vorstellen, welche zu einer Spirale verdreht ist. Die Holme entsprechen den Zucker – Phosphat Backbones, die Sprossen entsprechen den gepaarten Basen.
Allgemein
DNA Computing weist in den Grundzügen Ähnlichkeiten zu Parallel Computing auf. Anhand verschiedener DNA-Moleküle ist dieses Verfahren in der Lage eine Vielzahl an Möglichkeiten gleichzeitig zu bearbeiten. Bei bestimmten Spezialproblemen, wie z.B. dem NP-vollständigen-Problem, ist es theoretisch möglich, diese schneller und auf kleineren Raum zu lösen als mit konventionellen Prozessoren.
In einem Experiment wurde gezeigt, dass das Problem des Handelsreisenden mittels DNA-Computing lösbar ist. In diesem Fall wurde für jede vorkommende Stadt ein Typ DNA-Fragment erzeugt. Diese DNA-Fragmente waren in der Lage eine Bindung zu anderen DNA-Fragmenten gleichen Typs einzugehen. Mittels Reagenzglas entstanden binnen Sekunden aus den kleineren DNA-Fragmenten größere, welche dann die jeweiligen Reiserouten repräsentierten. Durch chemische Reaktionen wurden im Nachhinein DNA-Fragmente, die längere Reiserouten repräsentierten, eliminiert. Somit war man mit der Methode in der Lage das Problem zu lösen, da das entstandene DNA-Fragment die Lösung enthielt. Mit den damaligen Mitteln war man aber noch nicht in der Lage, die Lösung auszuwerten und somit wird dieses Experiment eher als Machbarkeitsnachweis gezählt.
Vorteile
- Hohe Speicherdichte der DNA: $1bit/nm^3$. Bei einem 1 Liter Lösung mit 6g DNA existiert eine Speicherkapazität von $3\cdot10^{19}$ Terabyte
- DNA ist in großer Anzahl im Reaktionsgefäß vorhanden und kann mittels PCR (Polymerase-Kettenreaktion) vervielfältigt werden. (Hohe Speicherredundanz)
- Operationen wirken fast alle gleichzeitig auf alle Stränge. (Massive Parallelität)
- Jedes denkbare Problem kann theoretisch bearbeitet werden.
- Höhere Haltbarkeit der Daten als bei digitalen Speichermedien.
Nachteile
- Langwierige Aufarbeitung der Rechenergebnisse notwendig.
- Die Menge der benötigten DNA wächst exponentiell mit dem Aufwand eines Problems. Im Falle des Handelsreisenden bräuchte man bei einer Anzahl von 200 Städten eine Menge an DNA, welche vergleichbar mit der Masse der Erdkugel ist.
Evolutionäre Algorithmen
Motivation
Als Evolution bezeichnet man allgemein die stammesgeschichtliche Entwicklung von niederen zu höheren Lebensformen. Damit ist die Evolution einer der grundlegendsten Prozesse in der Natur. Mit Hilfe dieser können Arten bzw. Populationen sich u. a. an veränderte Bedingungen anpassen. Dies geschieht durch Faktoren wie der Mutation, der Selektion und der Rekombination. Sie dienen dazu, die Anpassung an die jeweiligen Bedingungen zu optimieren und somit die Chancen zu erhöhen, die Existenz der Population sicherzustellen. Die evolutionären Algorithmen nehmen sich die genannten drei Hauptfaktoren als Vorbild und versuchen damit Lösungen von deterministisch schwer oder nicht lösbaren Problemen, wie z.B. den NP-vollständigen Problemen, zu finden.
Einführung
Anders als bei dem DNA-Computing, welches sich auf das einzelne Individuum bezieht, werden bei den evolutionären Algorithmen ganze Populationen und deren genetisch bedingte Entwicklung betrachtet. Dadurch spielen die Grundlagen der Populationsgenetik in dem Gebiet der evolutionären Algorithmen eine wichtige Rolle. Im Folgenden werden die drei in der Motivation genannten Hauptfaktoren aufgeschlüsselt und erklärt.
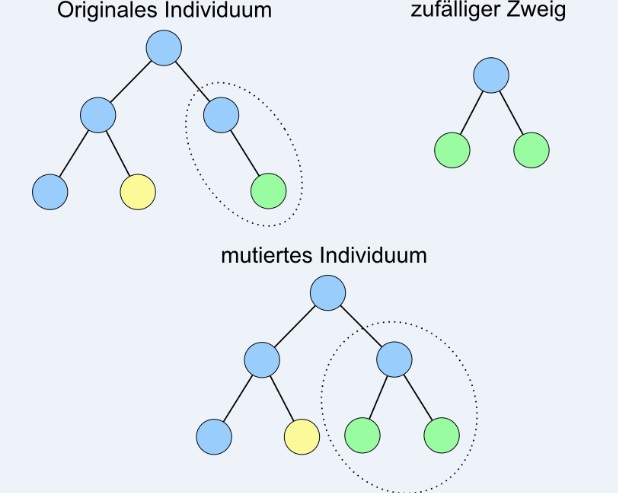
Mutation
Die Mutation als stochastischer Einflussfaktor ist in der Lage, neue Varianten zu finden und somit festzustellen, ob diese für die jeweiligen Bedingungen eine verbesserte Anpassung darstellen oder ungeeignet sind. Am Genpool einer Population sorgen sie i. d. R. nur für geringfügige Veränderungen, für die Evolution sind sie aber ein wichtiger Bestandteil, da sich viele verschiedene Mutationen zu einer signifikanten Gesamtänderung summieren können.
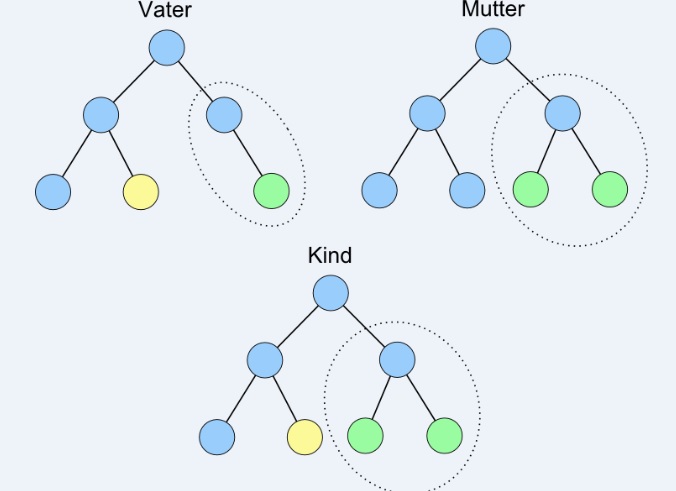
Rekombination
Die Rekombination beschreibt den Prozess, aus dem vorhandenen Erbgut zweier Individuen Erbgut für ein Nachkommen zu erzeugen, welches sich aus dem alten Erbgut zusammensetzt. Durch diesen Prozess ist es möglich, Kombinationen zu finden, welche dem Optimum näher kommen als die vorhandenen.
Selektion
Die Selektion beschreibt den Prozess, bei dem sich nur die vorteilhaftesten Eigenschaften einer Population durchsetzen. In der Natur selbst wird damit kein höheres Ziel angestrebt, sondern lediglich eine optimale momentane Anpassung angestrebt. Bei evolutionären Algorithmen kann anhand der sogenannten Fitnessfunktion kann genau abstrahiert werden, welche Eigenschaften positiv bzw. negativ zu bewerten sind.
Die Fitnessfunktion ist die Zielfunktion eines evolutionären Algorithmus. Genauso wie bei den evolutionären Algorithmen im Allgemeinen liegt auch hier ein biologisches Vorbild zugrunde, die sogenannte biologische Fitness. Sie gibt den Grad der Anpassung eines Organismus an seine Umgebung an. Bei den evolutionären Algorithmen besagt die Fitness eines Lösungsansatzes, wie gut er das Optimierungsproblem löst. Da es zumeist ausreichend ist, bestimmte Ansätze zu vergleichen, um den besseren zu selektieren, muss die Fitnessfunktion nicht zwangsläufig einen absoluten Wert berechnen können. Eine relative Angabe der Fitness genügt in manchen Fällen (z.B. Turnierselektion – „Kandidat a ist besser als b“). In dem Fall, dass eine Lösung zu n Problemen gleichzeitig gesucht wird und diese Probleme nicht zusammengefasst werden können, wird die Fitnessfunktion nicht als Einzelwert, sondern als n-Tupel angegeben.
Allgemein
In den folgenden Teilabschnitten werden kurz die verschiedenen Ausprägungen der evolutionären Algorithmen vorgestellt. Dabei wird das Hauptaugenmerk auf die Beschreibung genetischer Algorithmen gelegt, um ein grundlegendes Verständnis für deren Methodik zu vermitteln. Anschließend werden die Methodiken der verbleibenden drei Ausprägungen, der Evolutionsstrategien, der evolutionären und der genetischen Programmierung, skizziert. Zu beachten ist hier, dass diese strikte Trennung der vier klassischen Ausprägungen in aktuellen Anwendungen zumeist nicht mehr zu finden ist und stattdessen eine große Zahl von Mischformen existiert.
Genetische Algorithmen
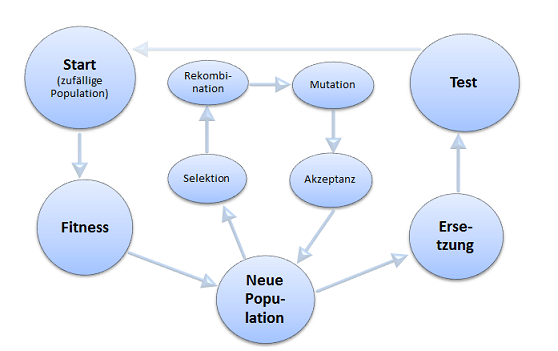
Genetische Algorithmen (GA) gehören allgemein in das Gebiet der evolutionären Algorithmen und haben die Evolutionstheorie nach Darwin zum Vorbild. Die Grundidee ist dabei, dass sich eine gefundene Lösung eines Problems mit der Zeit entwickelt und verbessert, es sind also naturanaloge Optimierungsprozeduren. Diese Anwendung eines aus der Biologie stammenden Konzeptes geht zurück auf den amerikanischen Mathematiker und Informatiker John Henry Holland. Dieser hat 1975 den Grundstein für unsere heutige Idee der GA gelegt und somit den Ablauf eines GA schematisch wie in Abb.2 dargestellt.
Den Anfang eines GA bildet eine Reihe zufälliger erster Lösungen (oder „Individuen“), die bereits das Problem lösen. Kern des ersten Hauptschrittes ist damit die Erzeugung von Zufallszahlen und die Bestimmung von Realisierungen, welche für das gegebene Problem Lösungen darstellen. Danach erfolgt im zweiten Hauptschritt eine Bewertung der Fitness jedes Individuums der Population mittels einer Fitnessfunktion f(x). Im dritten Hauptschritt wird eine neue Population geschaffen, indem die folgenden vier Prozesse solange wiederholt werden, bis die neue Population vollständig ist. Zuerst findet die Selektion statt, d. h. anhand der Fitnessfunktion werden jene Individuen gefunden, durch deren Kombination die besten Nachfolger entstehen. Dabei gilt je besser die Fitness ist, desto größer ist die Chance bei der Selektion ausgewählt zu werden. Anschließend wird die Kombination der Individuen durch die sogenannte Rekombination optimiert. Würde keine Rekombination stattfinden, wären alle Nachfolger jeweils nur eine exakte Kopie ihrer Eltern. Auf die Rekombination folgt die Mutation, um den Genpool der Individuen aufzufrischen. Dabei werden neue, zufällige Kombinationsvarianten zugelassen. Die so entstandenen Nachfolger werden wiederum bewertet. Bei Akzeptanz werden sie in die neue Population aufgenommen und sonst beginnen die vier Prozesse erneut, bis sich auf iterativem Wege eine akzeptable Lösung ergibt. Im vierten Hauptschritt erfolgt ein erneuter Durchlauf des Algorithmus, indem die erstgenutzte Population durch die neue ersetzt wird. Auf diesem Weg kann abschließend getestet werden, ob die beste Lösung in der aktuellen Population gefunden wurde. Bei ausreichender Lösung wird der GA an dieser Stelle beendet, andernfalls startet der Algorithmus erneut beim zweiten Hauptschritt.
Durch den zufälligen Charakter der Mutation ist diese Prozesskette, wie auch der Ausgangspunkt des Algorithmus, nicht-deterministisch und damit ist zu Anfang des GA nicht bestimmbar, wie viele Generationen von Individuen zur Erzeugung einer akzeptablen Lösung benötigt werden.
Evolutionsstrategien
Genetische Algorithmen bilden nicht den einzigen Ansatz für die Digitalisierung einer evolutionären Entwicklung. 1973 stellten die deutschen Informatiker Ingo Rechenberg und Hans-Paul Schwefel von der TU Berlin mit „Evolutionsstrategie“ das entscheidende Schriftstück zu Evolutionsstrategien (ES) vor. In der Grundidee, die Natur als Vorbild zur Lösung eines Optimierungsproblems zu nehmen, gleichen sich ES und GA. Grundlegende Unterschiede werden jedoch in der Wichtigkeit und Verwendung von Mutation und Selektion deutlich. Im Gegensatz zu den GA, wo die Mutation nur von geringer Bedeutung als zerstreuender Effekt ist, spielen in ES Mutation und Selektion eine zentrale Rolle. Während die Mutation bei beiden Ansätzen unabhängig von der Anzahl der Eltern aus einem Individuum ein neues erzeugt, wird sie bei GA klassisch durch das zufällige Invertieren einzelner Bits erzeugt und bei ES durch normalverteilte Veränderungen der Bits. Hinzu kommt der Einsatz selbstadaptiver Steuerungselemente der Parameter bei ES. Gemeint damit ist, dass jedes Individuum zusätzlich eine Information für die Mutationsstärke besitzt.
Evolutionäre Programmierung
Die Theorie der evolutionären Programmierung (EP) findet ihren Ursprung in dem 1966 von Lawrence Jerome Fogel, Alvin J. Owens und Michael John Walsh veröffentlichten Buch „Artificial Intelligence Through Simulated Evolution“. Im Unterschied zu klassischen GA und ES spielte dabei jedoch nicht die Optimierung der Lösung eines Problems die entscheidende Rolle, sondern die Entwicklung eines künstlich-intelligenten Automaten, der zur selbstständigen Lösung von Problemen in der Lage sein sollte. Der grundlegende konzeptuelle Unterschied zwischen GA/ES und EP besteht im Wesentlichen darin, dass bei erstgenannten die einzelnen Lösungen als Individuen interpretiert werden, wohingegen bei EP die Lösungen als Populationen interpretiert werden. Entsprechend wird bei EP auf genetische Operationen wie die Rekombination gänzlich verzichtet. Einzig die Mutation wird in der EP angewendet, wobei diese nicht auf einzelnen Bits ausgeführt wird wie bei GA und ES, sondern eine geringfügige Veränderung der Gesamtlösung, also der Population, darstellt.
Genetische Programmierung
Die genetische Programmierung (GP) basiert im Gegensatz zu allen drei zuvor genannten Klassen evolutionärer Algorithmen nicht darauf, die Lösung eines Optimierungsproblems zu finden, sondern auf der Idee Computerprogramme zu entwickeln, die selbst ein Problem lösen können. In ihrer modernen Form geht die GP auf den Informatiker John R. Koza und dessen Buch mit dem Titel „Genetic Programming: On the Programming of Computers by Means of Natural Selection“ (1992) zurück.
Beispiel
Neuronale Netze
Motivation
Es gibt Arten von Problemen, welche nicht oder nur sehr schwer anhand von Algorithmen gelöst werden können. Dazu gehören unter anderem Frühwarnsysteme oder auch Zeitreihenanalysen. Die dazugehörigen Daten sind von sehr vielen unterschiedlichen Faktoren abhängig und lassen sich deswegen nicht ohne weiteres in einen Algorithmus implementieren. Das Problem besteht darin, dass ein Computer komplexe mathematische Operationen ausführen kann, allerdings nicht lernfähig ist. Ein Ansatz für die Lösung dieses Problems stellen die aus der Gehirnforschung bekannten Neuronalen Netze dar. Anhand dieser wird die Anwendung von mathematischen Modellen, den sogenannten künstlichen neuronalen Netzen, möglich, welche „lernfähig“ sind und somit einen Lösungsansatz für die beschriebenen Probleme darstellen.
Biologische Grundlagen
Anhand von neuronalen Netzen wird versucht die Struktur und Informationsarchitektur eines Nervensystems von Menschen abzubilden. Sie bestehen aus Neuronen, Gliazellen und einer Umgebung. Die Gliazelle ermöglicht die gegenseitige elektrische Isolation der Nervenzellen. Viel wichtiger für die Funktionsweise eines neuronalen Netzes sind die Neuronen bzw. Nervenzellen. Diese dienen zur Aufnahme, zur Verarbeitung und zur Weiterleitung von Reizen.
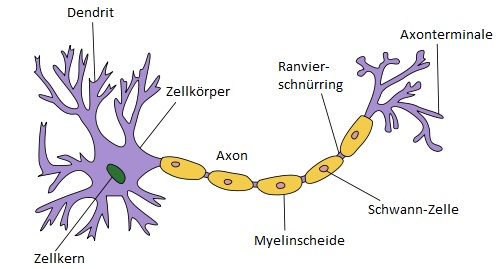
Aufbau Neuronen
Neuronen bestehen aus Dendriten, Zellkörper, Zellkern, Axon, Myelinscheide, Schwann-Zelle, Ranvierschnürring und Axonterminalen. Zur Erregung eines Neurons läuft das elektrische Signal durch das Axon. Das Axon ist zuständig für die Übertragung eines Aktionspotenziales. Mit Hilfe der Axonterminale kann das Signal chemisch an andere Neuronen bzw. Empfängerzellen weitergeleitet werden. Die Axonterminale selber sind mit den Dendriten anderer Zellen verbunden. Diese sind feine Verästelungen und dienen dazu Signale anderer Zellen zu empfangen und gegebenenfalls weiterzuleiten.
Übertragung von elektrischen Reizen
Zwischen der Umgebung und dem Axon besteht ein bestimmter Spannungsunterschied, dieser Zustand wird als Ruhepotential bezeichnet. Der Wert des Spannungsunterschiedes ist unterschiedlich, da z.B. die Gliahülle stark ausgebildet sein kann. Durch einen Reiz ändert sich die Spannung. Falls das Ruhepotential überschritten wird gibt das Axon die Differenz von Ruhepotential und Erregung als Aktionspotential an die Axonterminale weiter. Durch die Dendrite anderer Zellen wird das Aktionspotential aufgenommen und wiederum mit dem bestehenden Ruhepotential des Neurons abgeglichen.
Künstliche neuronale Netze
Ein künstliches neuronales Netz (KNN) ist ein mathematisches Modell, welchem der Aufbau und die Eigenschaften eines neuronalen Netzes zu Grunde liegen. Man verknüpft einzelne, simple Recheneinheiten (Perzeptron = analog zu Neuron) und gewichtet die Stärke der Bindung zwischen jeweils zwei Perzeptronen. Wird ein Gewicht positiv gewertet bedeutet dies einen erregenden Einfluss zwischen zwei Perzeptronen. Ist das Gewicht negativ gewertet, existiert ein hemmender Einfluss. Kein Einfluss existiert bei einem Gewicht von null. Zum Anfang eines jeweiligen KNN lassen sich nicht die gewünschten Ausgaben bestimmter Ein-Ausgabe-Paare herstellen. Dies geschieht erst durch die Wiederholung bestimmter Trainingsmuster. Die Trainingsmuster beinhalten bestimmte Lernregeln und modifizieren die Gewichte der einzelnen Perzeptronenpärchen. Das Wissen eines KNN wird somit in den Gewichten der Neuronen gespeichert.
Die Basiseinheit Perzeptron
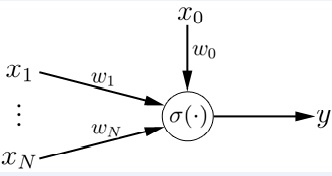
Ein künstliches Neuron eines KNN ist equivalent zu einem Neuron im biologischen Sinne. Beide verknüpfen viele Eingangssignale über eine bestimmte Funktion mit einem Ausgangssignal. Die einfachste klassische Realisierung eines KNN stellt einsogenanntes Perzeptron dar, auch bekannt als das klassische „Ur-Neuronenmodell“, welches 1958 von Frank Rosenblatt ursprünglich zur Simulation der Netzhaut des menschlichen Auges entwickelt wurde. Ein Perzeptron enthält die Summe aller gewichteten Eingangssignale und eines fixen Eingangssignals $x_0 = 1$, das mit dem Gewicht $\omega_0$ gewichtet wird, und bildet diese Summe $s$ über eine Transfer- oder Aktivierungsfunktion $\sigma$ auf das Ausgangssignal $y$ ab.
\[Y=\sigma(s)=\sigma(\omega^T \cdot x)=\sigma \left(\omega_0 + \sum_{i=1}^N \omega_i \cdot x_i \right)\]
Insbesondere bezeichnet man das feste Eingangssignal $\omega_0$ auch als Offset oder Bias. Mathematisch ausgedrückt kann die Summe $s$ auch als das Skalarprodukt der Eingangssignale $x=[1,x_1,\dots,x_N]^T$ mit dem Vektor der Gewichte $\omega= [\omega_0, \omega_1,\dots, \omega_N]^T$ bezeichnet werden. Symbolisch kann ein Perzeptron damit wie in folgender Abbildung dargestellt werden:
Die Auswahl der Transferfunktion orientiert sich in der Regel an der Art der Anwendung des KNN. Häufig verwendete Transferfunktionen sind unter anderem lineare Funktionen und Signum- oder Stufenfunktionen. Dabei gibt es keine konkreten Empfehlungen, wann welche Funktion angemessen ist. Allgemein kann gesagt werden, dass es in Analogie zum Gehirn vernünftig ist eine Transferfunktion auszuwählen, die in ihrem Wertebereich beschränkt ist. Auch ein biologisches Neuron kann nur ein endlich starkes Ausgangssignal erzeugen. Eine weitere allgemeine Empfehlung zur Wahl der Transferfunktion ist die Differenzierbarkeit. Grund hierfür ist, dass verschiedene Lernregeln, die eine Methode zur Bestimmung der Gewichte $\omega$ mit Hilfe von Trainingsdaten unter Vorgabe grober Randbedingungen angeben, eine differenzierbare Transferfunktion voraussetzen. Zusammenfassend ist zu sagen, dass ein Perzeptron durch die Eingangssignale $x$ und deren Gewichte $\omega$ sowie die Transferfunktion $\sigma$ vollständig beschrieben ist. Es spielt dabei keine Rolle, ob die Eingangssignale von einer Schnittstelle außerhalb des KNN stammen oder von vorgeschalteten Perzeptronen.
Aufbau von KNN
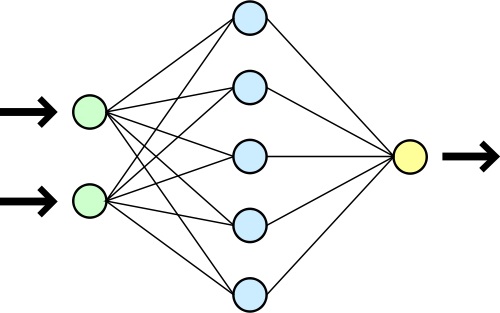
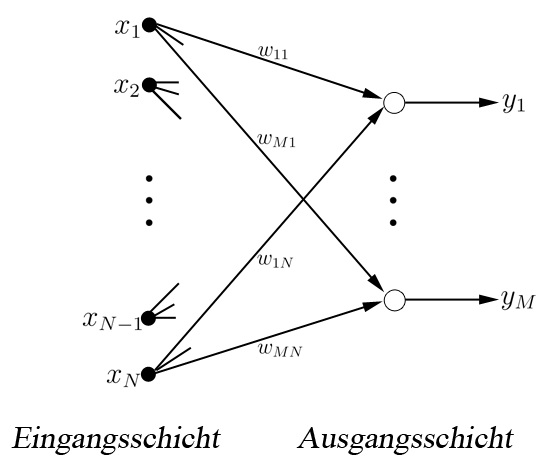
Der grundsätzliche Aufbau eines klassischen KNN besteht aus der Vernetzung vieler einzelner Perzeptronen, die in parallel geordneten Schichten, den sogenannten Layers, zusammengefasst werden. Dabei wird eine Klassifizierung von KNN anhand der Art der Vernetzung zwischen den Schichten vorgenommen. Diese Einteilung wird auch als Topologie der KNN bezeichnet. Beispiele für verschiedene Topologien sind unter anderem vorwärtsgerichtete (Feedforward) Netze und rückgekoppelte (Feedback) Netze. Bei Feedforward Netzen sind von jedem Perzeptron einer Schicht nur Vernetzungen in Perzeptronen der nächsten Schicht in Richtung des Ausgangssignals $y$ erlaubt. Eine weitere Unterteilung repräsentieren hier bspw. die Feedforward Netze mit Shortcut Connection. Darin sind zudem Vernetzungen zwischen Perzeptronen erlaubt, die eine Schicht überspringen. In Erweiterung zu Feedforward Netzen erlauben Feedback Netze zudem, dass sich ein Perzeptron über beliebige Vernetzungen selbst beeinflussen kann. Dabei gibt es auch für Feedback Netze verschiedenste Varianten, wie bspw. die direkte Rückkopplung, bei der einzelne Perzeptronen zu sich selbst verbunden sind, aber nicht zu Perzeptronen aus vorangegangenen Schichten.
Allgemein besteht jedes KNN aus einer Eingabeschicht, einer oder mehreren versteckten Verarbeitungsschichten, den sogenannten versteckten Schichten, und einer Ausgabeschicht. Eine namentliche Charakterisierung verschiedener KNN erfolgt zumeist durch die Bezeichnung „n-schichtig“, wobei n die Anzahl der versteckten Schichten plus der Ausgabeschicht ist. Mit zunehmender Zahl von Schichten eines KNN steigt zudem die Komplexität und damit auch die Anwendbarkeit auf komplizierte Probleme. Wenn mit einem 1-schichtigen Netz lediglich lineare Klassifikationsprobleme gelöst werden können, können dagegen mit einem 2-schichtigen Netz bereits beliebige Polynome approximiert werden.
Beispiel
Eines der grundlegendsten Beispiele zur Anwendung von KNN stellt die Realisierung der booleschen AND-Operation dar. Diese kann mittels eines 1-schichtigen KNN und eines einzigen Perzeptrons dargestellt werden. Gegeben sind zwei binäre Variablen $x_1$ und $x_2$. Die AND-Operation verknüpft die beiden Operanden gemäß folgender Tabelle.
| Fall | $x_1$ | $x_2$ | $x_1$ AND $x_2$ | Gewünschte Ausgabe |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 AND 0 | 0 |
| 2 | 0 | 1 | 0 AND 1 | 0 |
| 3 | 1 | 0 | 1 AND 0 | 0 |
| 4 | 1 | 1 | 1 AND 1 | 1 |
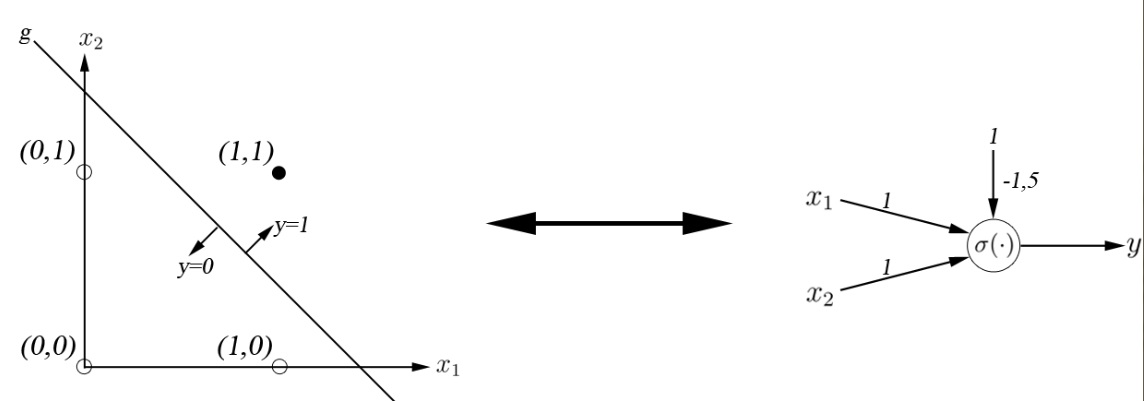
Anschaulich vorstellen kann man sich das Beispiel durch die graphische Darstellung. Deutlich wird dabei, dass es sich um ein Klassifikationsproblem handelt, wobei sich die Eingangs- und Ausgangssignale als Koordinaten in einem zweidimensionalen Koordinatensystem darstellen lassen. Es ist möglich, die Punkte $(x_1, x_2) = (0,0), (0,1), (1,0) $ von dem Punkt $(x_1, x_2) = (1,1)$ durch eine Gerade $g$ der folgenden Art zu trennen. \[g: \omega_0 + \omega_1 x_1 + \omega_2 x_2 = 0\]
Durch manuelles Einstellen der Gewichte lässt sich herausfinden, dass die Gerade $g$ eine gewünschte Klassifikation vornimmt, wenn als Gewichte $\omega_0=-1.5, \omega_1=1, \omega_2=1$ vergeben werden. Damit lässt sich das Perzeptron durch folgende Transferfunktion vollständig beschreiben: \[Y= \sigma( -1.5 + x_1 + x_2 )\]
Die sogenannte Aktivierung wird $y=0$ für alle unterhalb der Geraden liegenden Punkte $((x_1, x_2) = (0,0), (0,1), (1,0))$ und $y=1$ für alle oberhalb liegenden Punkte $((x_1, x_2) = (1,1))$.
Vorteile
- Mathematische Funktionen von beliebiger Art sind implementierbar.
- Es bieten sich vielfältige Anwendungsmöglichkeiten auch über das mathematische Kernproblem hinaus. Ein Beispiel ist das in [2] beschriebene Problem der Gesichtsausdruckserkennung.
- Robust auch bei verrauschten Eingangsdaten.
Nachteile
- Es erfolgt eine implizite Repräsentation von Wissen, verteilt in den Gewichten zwischen den Schichten. Damit eine Art Black-Box.
- KNN’s weisen eine sehr hohe mathematische Komplexität und mangelnde Erklärbarkeit ihrer Wirkungsweise und ihres Verhaltens auf.
Übungsaufgaben
DNA-Computing
1. Setzen Sie sich mit der Visualisierung des DNA-Stranges auseinander und versuchen Sie das System der DNA und der einzelnen vier Basen zu verstehen.
Evolutionäre Algorithmen
2. Untersuchen Sie die auf der folgenden Seite im unteren Bereich befindlichen Applet's zum Thema Evolutionäre Algorithmen. Varieren Sie die verschiedenen Parameter, um somit die Lösung zu optimieren.
Evolutionäre Algorithmen Applet's
3. Welche dieser Optimierungsprobleme sind für genetische Algorithmen geeignet, welche nicht? Begründen Sie Ihre Antwort.
- Wir wollen das Minimum einer mathematischen Funktion finden, von der wir die Ableitungen analytisch berechnen können.
- Wir wollen eine neue Tomate züchten, welche sich möglichst gut in viereckigen Schachteln verpacken lässt.
- Wir wollen die Noten der letzten Prüfung mit unlauteren Mitteln ein bisschen verbessern. Um an diese zu gelangen, müssen wir ein achtstelliges Passwort des Lehrers im Computersystem der Schule, bestehend aus Buchstaben und Zahlen, erraten.
- Wir wollen ein Computerprogramm schreiben, welches das Maximum einer beliebigen Funktion errechnet. Von der Funktion weiss das Programm nichts, es darf es aber an beliebigen Stellen auswerten.
Neuronale Netze
4.
Setzen Sie sich sich nochmal mit dem Beispiel der AND-Operation auseinander. Versuchen Sie die Grundlagen nachzuvollziehen und probieren Sie im weiteren Verlauf die Gewichte des Vektors $\omega= [\omega_0, \omega_1,\dots, \omega_N]^T$ so zu ändern, dass die AND-Operation weiterhin ausgeführt werden kann.
5.
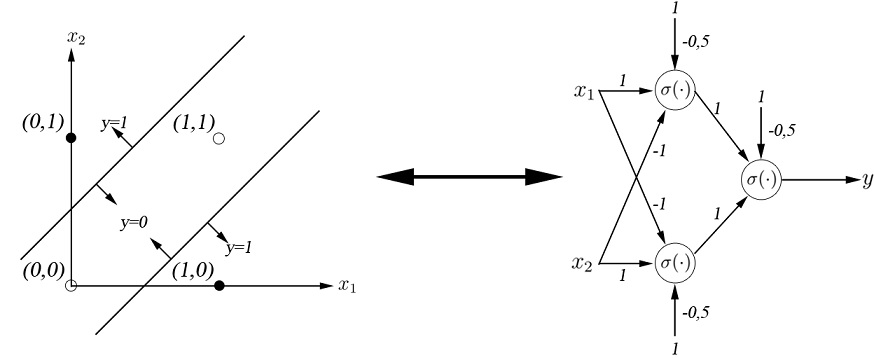
Versuchen Sie mit Hilfe der künstlichen neuronalen Netze die boolsche XOR-Operation zu lösen.
Lösungen
3.
5.
Literatur
[1] Christian Wagenknecht Algorithmen und Komplexität. Fachbuchverlag Leipzig, 2003, ISBN 3-446-22314-2
[2] Christine L. Lisetti, David E. Rummelhart. Facial Expression Recognition Using a Neural Network. In Proceedings of the Eleventh International Florida Artificial Intelligence Research Society Conference, 328-332, 1998
Weblinks
[1] Wikipedia DNA
[2] Wikipedia Neuronales Netz
[3] Wikiversity Genetische Algorithmen
[4] Uni Saarland DNA Computing
[5] Uni Münster Neuronale Netze
sortierte Listen
Allgemein
Bei einer sortierten Liste sind die Knoten nicht in der sequentiellen Reihenfolge ihrer Eingabe angeordnet, sondern werden nach bestimmten Sortierkriterien (z.B. aufsteigend oder absteigend) geordnet.
Sortierte Listen haben Vorteile gegenüber unsortierten Listen – Daten können schneller aufgefunden werden – dies gilt insbesondere für beidseitig verkettete Listen. Denn es kann schon vor Beginn des Suchvorgangs ermittelt werden, ob das gesuchte Element eher am Ende oder am Anfang der Liste zu finden sein wird. Entsprechend kann der Suchvorgang am Ende oder am Anfang der Liste begonnen werden, was die Suchzeit erheblich verkürzt.
Aufbau
Der interne Aufbau einer sortierten Liste unterscheidet sich nur unwesentlich von einer unsortierten Liste. Wichtig ist, dass sie nicht nachträglich sortiert (wie z.B. bei Arrays üblich), sondern von Anfang an sortiert aufgebaut wird. Das heisst: Bereits beim Einfügen eines neuen Elements erhält dieses seine richtige Position in der Sortierreihenfolge - ein neuer Knoten wird nicht einfach an das Listenende angehängt, sondern an der passenden Position in die Liste eingefügt.
Einfügevorgang
- Die Liste wird elementweise durchlaufen und dabei durch eine Vergleichs-operation mit den bereits vorhandenen Elementdaten die richtige Einfügeposition für den neuen Knoten bestimmt. Hierbei ist der Sortieralgorithmus zu beachten (aufsteigend oder absteigend etc.).
- Wenn die richtige Position Stelle gefunden ist, wird ein neuer Knoten erzeugt. Der Zeiger des vorausgegangenen Knoten wird auf den neu eingefügten Knoten gesetzt und der Zeiger des eingefügten Knotens auf den nachfolgenden Knoten. Entsprechend wird bei einer beidseitigen verketteten Liste auch der Rückzeiger versetzt.
//Bild "Knoten einfügen"//
Das Entfernen eines Datenelements verläuft analog: Auffinden des gesuchten Elements, dann Zeiger versetzen und Element löschen. Auch hierbei muss insbesondere das Versetzen der Zeiger sorgfältig programmiert werden, um das Zerbrechen der Liste und damit Datenverlust zu vermeiden.
Vorgehensweise
Eine sortierte Liste kann mit unterschiedlichen Algorithmen zum Auffinden der passenden Einfüge- bzw. Löschposition implementiert werden.
- Beim Durchlaufen der Liste wird nur ein einziger Suchzeiger benutzt. Zum Einfügen oder Löschen eines Elements muss dann jedoch ein temporärer Hilfszeiger verwendet werden, der die Adresse des folgenden Elements zwischenspeichert, bis die Operation abgeschlossen ist.
- Auf den temporären Hilfszeiger kann verzichtet werden, wenn zwei Suchzeiger zum Durchlaufen der Liste benutzt werden. Sie laufen im Schrittabstand parallel und zeigen auf die benachbarten Elemente.
temporärer Hilfszeiger
Im folgenden Beispiel soll der Datensatz "3" in eine sortierte Liste eingefügt werden. Der Suchzeiger steht zu Beginn am Listenkopf.
//Bild "temp Zeiger 1"//
Zum Auffinden der richtigen Einfügeposition rückt der Suchzeiger elementweise weiter. Dabei wird über den next-Zeiger das jeweils folgende Element geprüft, ob es grösser oder kleiner ist als das einzufügende.
//Bild "temp Zeiger 2"//
Wenn die Bedingung zutrifft, dann ist die richtige Einfüge-Position für das neue Element (3) gefunden. Nachdem das neue Element erzeugt wurde, kann der next-Zeiger des aktuellen Elements umgesetzt werden. Dies darf allerdings erst geschehen, nachdem ein temporärer Hilfszeiger (temp) die Adresse des nachfolgenden Elements gesichert hat. Dann kann der next-Zeiger des vorhergehenden Elements auf die Adresse des neuen Elements gesetzt werden und der next-Zeiger des neuen Elements auf die Adresse des nachfolgenden Element, die im temporären Hilfszeiger aufbewahrt worden ist. Der Hilfszeiger wird danach nicht mehr gebraucht.
//Bild "temp Zeiger 3"//
zwei ständige Zeiger
Beim Durchlaufen der Liste können alternativ auch zwei Zeiger eingesetzt werden. Am Beginn des Suchlaufs zeigen beide Zeiger zunächst gemeinsam auf den Listenkopf.
//Bild "zwei 1"//
Beim folgenden Suchvorgang zeigt der nachfolgende Zeiger auf den jeweils vorhergehenden Knoten (weil dessen next-Zeiger auf den neuen Knoten umgesetzt werden muss) und der Suchzeiger auf den aktuellen Knoten. So durchläuft der search-Zeiger die Liste knotenweise bis zum Ende und vergleicht dabei die Daten jedes Knotens mit den Daten des einzufügenden Knotens. Der last-Zeiger bleibt also immer eine Position zurück.
//Bild "zwei 2"//
Wenn die passende Position für den neuen Knoten in der sortierten Liste gefunden ist, dann wird der next-Zeiger des last-Knotens auf den neuen Knoten gesetzt und der next-Zeiger des eingefügten Knotens auf den search-Knoten. Damit ist der neue Knoten in der sortierten Liste an der richtigen Position verankert.
//Bild "zwei 3"//