Motivation SS12
Aus ProgrammingWiki

Inhaltsverzeichnis |
Gibt es etwas Besseres als ...?
Algorithmen sind die leistungsfähigsten Problemlösungswerkzeuge, die wir kennen. Da Computer Algorithmen viel schneller und wesentlich zuverlässiger ausführen können als wir Menschen, findet man sie als Programme in zahlreichen Geräte, wie in Taschenrechnern, Laptops, elektrischen Haushaltgeräten und Autos.
Im Hinblick auf die Berechnungsgeschwindigkeit und den Speicherbedarf gibt es Unterschiede zwischen den Programmen. Hat man die Wahlmöglichkeit, so wird man sich für die Verwendung des Algorithmus' entscheiden, der das gewünschte Ergebnis schneller ermittelt als alle anderen, die es zur Lösung des betrachteten Problems gibt.
Der dadurch insgesamt erzielte Effekt kann beachtlich sein. Dies gilt insbesondere dann, wenn eine zeitsparendere Berechnung in anderen Kontexten wiederholt ausgeführt wird. Wie wir später sehen werden, geht es dabei mitunter nicht um ein paar Millisekunden, sondern um Tage, Monate oder sogar um Zeitabschnitte, die die Existenz unseres Sonnensystems übertreffen. Im letzten Fall werden Berechnungen durch bessere Algorithmen überhaupt erst möglich, falls man solche findet.
Im folgenden Kapitel betrachten wir Algorithmen zur Multiplikation zweier natürlicher Zahlen. Hierfür haben wir in der Schule ein schriftliches Verfahren kennengelernt. Es ist eher von kulturhistorischem Wert, denn man benutzt es praktisch nicht mehr. Taschenrechner erledigen das viel schneller. Fraglich ist allerdings, ob sie auch diese Schulbuchmethode verwenden. Oder geht es noch schneller? Letzteres wäre insofern interessant, als das Multiplikationen in beliebiger Anwendungssoftware millionenfach vorkommen. Schon kleine Effizienzverbesserungen hätten einen enormen Einfluss.
Algorithmen zur Multiplikation
Multiplikation großer Zahlen
In der Tat gibt eine bessere Methode zur Multiplikation zweier natürlicher Zahlen als die, die in der Schule gelehrt wird.
Doch was bedeutet "besser" und warum ist das wichtig?
- Ein besserer Multiplikationsalgorithmus benötigt weniger Zeit als andere Verfahren mit gleichem Resultat.
- Dadurch können alle Operationen, die zwei Zahlen großer Stelligkeit multiplizieren, viel schneller ausgeführt werden. Beispiele sind: Computeralgebrasysteme und Geometrieprogramme.
- Konsequenzen hat das auch für die Kryptografie.
Als erstes suchen wir eine Art Messmethode, mit der wir die Berechnungsgeschwindigkeiten ermitteln und untereinander vergleichen können.
Primitive Basisoperationen
Wir gehen davon aus, dass die folgenden beiden Elementaroperationen vorhanden sind und für die entsprechenden Eingaben stets mit konstantem Zeitaufwand ausgeführt werden.
- Addition dreier Ziffern (sog. Volladdierer)
Eingaben: x und y sowie der Übertrag c
Resultat: zwei Ziffern, nämlich die Ergebnisziffer und der neue Übertrag - Multiplikation zweier Ziffern
Eingaben: x und y
Resultat: zwei Ziffern, nämlich die Ergebisziffer und der Übertrag
Für diese beiden Operationen wird im Folg. je eine Scheme-Prozedur prim-add und prim-mult definiert. In diesen Definitionen wird die Basis $B$ der Zahlendarstellung durch den Wert der Variablen basis festgelegt. Die Voreinstellung ist $B=10$. Für den Fall, dass ein anderes Stellenwertsystem verwendet werden soll, ist diese Angabe anzupassen.
Die primitive Addition zweier Ziffern und eines Übertrags liefert ein Paar, dessen erstes Element die Einerstelle und das zweite den neuen Übertrag darstellt. Beispielsweise wird für $7+8+0=15$ das Paar (5 . 1) zurück gegeben.
Ein weiteres Aufrufbeispiel gilt der Multiplikation: $9\cdot 8=72$
Da die beiden primitiven Operationen mit komplexeren Scheme-Sprachelementen definiert wurden, macht es keinen Sinn, zur Aufwandsanalyse darauf aufbauender Operationen eine Zeitmessung durchzuführen. Sinnvoll ist es, als Aufwandsmaß die Gesamtanzahl der Aufrufe primitiver Basisperationen heranzuziehen. Hierfür wird eine globale Variable anzahl-prim-op als Zähler bereitgestellt und mit 0 initialisiert.
Addition und Multiplikation $n$-stelliger natürlicher Zahlen
Die Stelligkeit $n$ einer natürlichen Zahl ist eine Eigenschaft, die von deren Darstellung abhängt. Bereits in der Grundschule lernt man eine Methode zur Zahldarstellung durch die entsprechenden Ziffern in einem Stellenwert- oder Positionssystem mit einer gewählten Basis $B$. Typische Beispiele sind $B=10$ (Dezimalsystem), $B=2$ (Dualsystem) und $B=16$ (Hexadezimalsystem).
Die allgemeine Darstellung ist: $$a_{n-1}a_{n-2}\ldots a_1 a_0 = \sum_{i=0}^{n-1} a_i \cdot B^i, \text{ mit } n\in\mathbb{N}, n>0, \text{ und } a_i\in\{0,1,\ldots,B-1\}$$
Für $B=2$ gilt $a_i\in\{0,1\}.$
Für $B=10$ gilt $a_i\in\{0,1,2,3,4,5,6,7,8,9\}.$
Für $B=16$ gilt $a_i\in\{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F\}.$
Mit zwei Ziffern können alle Zahlen aus dem Intervall $[0,B^2-1]$ dargestellt werden, denn $(B-1)\cdot B^1+(B-1)\cdot B^0=(B+1)\cdot (B-1)= B^2-1.$
ÜA: Überprüfen Sie diese Aussage für $B=10$ und $B=16.$
Wir führen nun die Addition und Multiplikation n-stelliger Zahlen auf diese primitiven Operationen zurück.
Addition zweier $n$-stelliger natürlicher Zahlen
Im Folg. und bis auf Weiteres legen wir verabredungsgemäß $B=10$ zugrunde.
Beispiel: $1827634 + 8294678$ ($n=7$)
Typische Handrechnung Ausführlich: mit Übertrag
1827634 a 1827634 a
8294678 b 8294678 b
-------- 11111110 c Übertrag
10122312 s --------
10122312 s
Jetzt ist klar, weshalb die primitive Addition für zwei Ziffern und eine Übertragsziffer ausgelegt wurde. Für die Addition $a_i+b_i+c_i=s_i$ ergibt sich ein Übertrag $c_{i+1}=1$, wenn $s_i\geq B$, ansonsten ist $c_{i+1}=0$. Nehmen wir die beiden größtmöglichen Summanden $B-1$ und $B-1$. Dann ergibt sich für die Einersteller der Summe $a_i+b_i-B=(B-1)+(B-1)-B=B-2$, was offensichtlich mit einer Ziffer aus $[0,B-1]$ stets darstellbar ist.
Die Operation add kann nun angewandt werden, um die obige simple Beispielrechnung auszuführen. Für die beiden Summanden werden ihre Ziffernlisten übergeben:
Für die Addition zweier $n$-stelliger Zahlen werden $n$ Elementaradditionen benötigt. Auch dies gilt für das Beispiel.
ÜA: Modifizieren Sie das Beispiel und evaluieren Sie die zugehörigen Additionen.
Multiplikation einer $n$-stelligen natürlichen Zahl mit einer einstelligen
Für die Multiplikation zweier $n$-stelliger natürlicher Zahlen benötigen wir einen Zwischenschritt, um die primitive Addition geeignet einzubeziehen. Wir betrachten zunächst die Multiplikation einer $n$-stelligen natürlichen Zahl mit einer einstelligen.
Beispiel: $25367 \cdot 5$ ($n=5$)
25367 * 5
---------
005505 links mit Null aufgefüllt, um Primitivaddition zu ermöglichen
+ 121330 Übertrag, Stelle ganz rechts mit Null aufgefüllt
------
126835 durch Elementaraddition gewonnen
Der Übertrag $c_{i+1}$ kann hier größer ausfallen als bei der Addition ($0$ oder $1$). Offenbar gilt:
$$\begin{eqnarray*} z &=& a_i\cdot b_j \leq (B-1)^2 \leq B^2 - 2B + 1 \leq (B - 2)\cdot B + 1 \\ z &=& c_{i+1}\cdot B + d_i \leq (B-2)\cdot B + 1 \end{eqnarray*}$$
Der Kooeffizientenvergleich liefert $c_{i+1}\leq B-2$, d.h. die Übertragsziffer stammt aus $\{0,1,2,\ldots,B-2\}.$ Natürlich gilt $c_0=0.$
ÜA: Konkretisieren Sie den beschriebenen Sachverhalt für $B=10$ und $B=16$.
Das obige Ergebnis für die Beispielrechnung erhalten wir auch mit der vorbereiteten Operation mult1. mult1 nimmt eine Liste mit den Ziffern des ersten Faktors $a=a_{n-1}a_{n-2}\ldots a_1 a_0$ und eine Ziffer $b_j$ als zweiten Faktor und liefert das Produkt $a\cdot b_j$ als Ziffernliste.
Auch hierfür können wir die Zahl der Elementaroperationen (prim-add und prim-mult) bestimmen:
Wir rechnen nach:
- $n$ Elementarmultiplikationen
- $n+1$ Elementaradditionen
Zusammen sind das $2n+1$ primitive Basisoperationen, für $n=5$ sind das gerade $11$ Stück.
Multiplikation zweier $n$-stelliger natürlicher Zahlen
Nun folgt der Übergang zur vollen Multiplikation. Die hier (im Hintergrund definierte und) bereitgestellte Prozedur mult verwendet die Schulbuchmethode zur schriftlichen Multiplikation.
Beispiel: $8643 \cdot 9915$ ($n=4$)
8643 * 9915 ----------- 77787000 = mult1(8643,9) und rechts mit Nullen aufgefüllt 07778700 = mult1(8643,9) und links/rechts mit Nullen aufgefüllt 00086430 = mult1(8643,1) und links/rechts mit Nullen aufgefüllt 00043215 = mult1(8643,5) und links mit Nullen aufgefüllt -------- 85695345 = add(add(add(77787000,07778700),00086430),00043215) = mult(8643,9915)
Wir rechnen nach:
Natürlich interessieren wir uns für die Anzahl der primitiven Basisoperationen:
Die Multiplikation zweier $n$-stelliger natürlicher Zahlen nach der im Beispiel angewandten Methode führt zu $n$ Summanden. Jeder Summand entsteht als Teilprodukt und erfordert, wie wir weiter oben gezeigt haben, $2n+1$ Basisoperationen. Das ergibt für alle Summanden $n\cdot (2n+1) = 2n^2+n$ Elementaroperationen.
Die $n$ Summanden sind jeweils höchstens $2n$-stellig, denn der erste Summand ist ohne Auffüllnullen höchstens $n+1$-stellig. (Im Beispiel ist das der Fall.) Dann folgen $n-1$ weitere Summanden und folglich ebenso viele Rechtsverrückungen um eine Stelle. Das ergibt zusammen: $n+1+n-1=2n.$ (Die Auffüllung mit Nullen ist notwendig, um die Summanden gleichstellig zu machen.)
Die $n-1$ Additionen je eines höchstens $2n$-stelligen Summandens mit der jeweils aktuellen höchstens $2n$-stelligen Zwischensumme erfordert $(n-1)\cdot 2n = 2n^2-2n$ Elementaroperationen.
Fazit: Damit verursacht die Schulbuch-Multiplikationsmethode einen Aufwand von insgesamt $2n^2+n + 2n^2-2n = 4n^2-n$ primitiven Basisoperationen, wobei $n$ die Stelligkeit der Faktoren bezeichnet.
Für unser Beispiel ergibt sich:
Zur Analyse des Berechnungsaufwandes der betrachteten Multiplikationsmethode brauchen wir eine Prozedur zufallsliste zur Herstellung einer Liste mit $n$ zufällig gewählten Ziffern aus $[0;9]$.
Der folgende Aufruf liefert eine Liste mit 30 Zufallsziffern.
In folgendem Code kann die Stelligkeit der beiden Zufallszahlen (repräsentiert durch eine $n$-stellige Zufallsliste) durch Veränderung des Wertes für n leicht modifiziert werden. Bei jedem Aufruf werden neue Zufallslisten gebildet.
Wiederholte Ausführungen bestätigen, dass der Multiplikationsaufwand zwar von der Stelligkeit $n$ jedoch nicht von den konkreten Faktoren abhängt. Die Anzahl der erforderlichen primitiven Operationen bleibt für ein festes $n$ stets unverändert.
Schließlich wird der experimentell ermittelte Aufwand mittels mult zur Schulbuch-Multiplikation zweier $n$-stelliger natürlicher Zahlen in Abhängigkeit von $n$ grafisch dargestellt. Zum Vergleich wird der Graph der Funktion $n\mapsto 4n^2-n$ hinzugefügt.
Die Ergebnisse des Experiments stimmen mit den theoretischen Vorhersagen überein.
Rekursive Form der Multiplikation nach der Schulbuchmethode
Um ein alternatives Multiplikationsverfahren zu gewinnen, zerlegen wir die beiden jeweils $n$-stelligen Faktoren $a$ und $b$, mit $a,b\in\mathbb{N}$, in je zwei (möglichst) $k$-lange Teile. Für $a=123456$ sind das $123$ (höherwertiger Teil) und $456$ (niederwertiger Teil). Offensichtlich ist $k=\frac{n}{2}=\frac{6}{2}=3$ und somit gilt $a=123\cdot 10^3+456=123456$.
Allgemein gilt mit $k=\left\lfloor\frac{n}{2}\right\rfloor$: $$\begin{eqnarray} a &=& a_1 B^k + a_0 \\ b &=& b_1 B^k + b_0 \\ \hline \\ a\cdot b &=& a_1\cdot b_1\cdot B^{2k}+(a_1\cdot b_0+a_0\cdot b_1)\cdot B^k+a_0\cdot b_0 \end{eqnarray}$$
ÜA: Rechnen Sie den für $a\cdot b$ angegebenen Ausdruck nach.
Offensichtlich werden zur Berechnung von $a\cdot b$ nach der obigen Zerlegung 4 Multiplikationen $\left\lceil\frac{n}{2}\right\rceil$-stelliger und 3 Additionen höchstens $2n$-stelliger Zahlen benötigt. Dies gilt für (vorzugsweise Zweierpotenzen) $n\geq 2$. Falls $n=1$ reduziert sich der Aufwand auf die Ausführung einer Elementarmultiplikation mit Aufwand $1$. Die folgende sog. rekurrente Gleichung fasst dies zusammen:
$$T(n) = \begin{cases} 1, & \text{wenn } n = 1 \\ 4\cdot T\left(\left\lceil\frac{n}{2}\right\rceil\right)+3\cdot 2n, & \text{wenn } n \geq 2 \end{cases}$$
Genau genommen müssten wir eine Ungleichung angeben, denn der rechte Ausdruck beschränkt den Aufwand, also den Wert von $T(n)$ nach oben.
Da solche rekurrenten Beziehungen den Aufwand rekursiver Verfahren unmittelbar beschreiben und deshalb recht oft vorkommen, lohnt es sich über deren Lösungsmethoden nachzudenken. Wir machen hier von diesen Methoden Gebrauch, indem wir das folgende Resultat zitieren:
$$T(n) = \begin{cases} 7n^2, & \text{wenn } n \text{ eine Zweierpotenz ist}\\ 28n^2, & \text{für alle anderen } n \end{cases}$$
wobei wir es auch hier wieder den größtmöglichen Aufwand zugrunde gelegt haben.
ÜA: Verwenden Sie die Meistermethode, um $T(n)=\mathcal{O}(n^2)$ als Lösung obiger Rekurrenz zu bestätigen.
Fazit: Leider müssen wir feststellen, dass die rekursive Methode der Schulbuchmultiplikation gegenüber der ersten Variante keinen Effizienzvorteil bietet. Beide arbeiten mit quadratischem Aufwand.
Die Karatsuba-Methode
Dem sowjetischen Mathematiker Karatsuba fiel 1962 auf, dass die Berechnung von $a\cdot b$ bei gleicher Zerlegung wie oben auch anders organisiert werden kann. Der von ihm angegebene Ausdruck $$\begin{eqnarray} a\cdot b &=& a_1\cdot b_1\cdot B^{2k}+((a_1+a_0)\cdot (b_1+b_0) - (a_1\cdot b_1+a_0\cdot b_0))\cdot B^k+a_0\cdot b_0 \end{eqnarray}$$ enthält 3 Multiplikationen $\frac{n}{2}$-stelliger und 6 Additionen (inkl. einer Subtraktion) höchstens $2n$-stelliger Zahlen. Das Besondere an diesem Term ist, dass einige Produkte, nämlich $a_1\cdot b_1$ und $a_0\cdot b_0$ mehrfach auftauchen. Sie brauchen nur einmal berechnet zu werden. Auf diese Weise kann eine (teure) Multiplikation mit drei (billigeren) Additionen erkauft werden.
ÜA: Überprüfen Sie den für $a\cdot b$ angegebenen Ausdruck durch Rechnung.
Dies ergibt einen Gesamtaufwand, der sich durch folgende Rekurrenz beschreiben lässt: $$T(n) = \begin{cases} 3n^2+2n, & \text{wenn } n \leq 3 \text{ (Schulbuchmethode)}\\ 3\cdot T\left(\left\lceil\frac{n}{2}\right\rceil+1\right)+6\cdot 2\cdot n, & \text{wenn } n \geq 4 \end{cases}$$
Die Lösung dieser Gleichung ist $$T(n) = 99 n^{\log_23} + 48n + 48 \log_2n\text{ für alle } n. $$
ÜA: Verwenden Sie die Mastermethode zur Lösung der Rekurrenz $T(n)=3T\left(\frac{n}{2}\right)+12n$. Verwenden Sie die Näherung $\log_23\approx 1.58$.
Insbesondere für große $n$ ist diese Methode von Vorteil. Um festzustellen, ab welchem Wert $n_0$ die Karatsuba-Multiplikation der Schulbuchmethode überlegen ist, stellen wir beide in einem Diagramm grafisch dar.
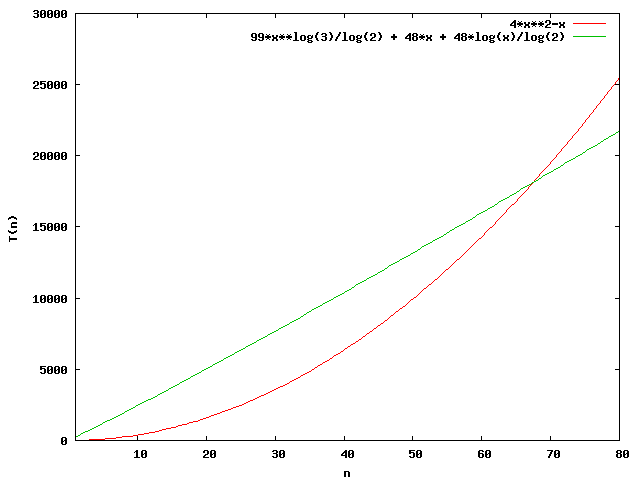
Fazit: Ab $n_0=70$ ist die Karatsuba-Multiplikation zweier $n$-stelliger natürlicher Zahlen die effizientere Methode.