Komplexitätstheorie und NP-vollständige Probleme
Aus ProgrammingWiki
In den bisherigen Kapiteln wurden verschiedene Probleme behandelt und deren Lösungsaufwand analysiert. Für einige von ihnen haben wir effiziente Algorithmen gefunden. Effizient bedeutet dabei, dass die Laufzeit durch ein Polynom (möglichst geringen Grades) in der Problemgröße nach oben beschränkt werden konnte.
Leider gibt es sehr viele Probleme, für die das nicht möglich ist. Beispielsweise konnte für das 0/1-Rucksackproblem selbst mit Dynamic Programming in Bezug auf die Stelligkeit der Eingabe nur ein Exponentialzeit-Algorithmus gefunden werden. Zahlreiche Probleme mit großer praktischer Relevanz sind ähnlich schwer. Ein Beispiel ist die Primfaktorzerlegung einer natürlichen Zahl. Aus der Zahlentheorie ist bekannt, dass jede natürliche Zahl eine eindeutige Primfaktorzerlegung besitzt. Um sie zu bestimmen, "braucht man ggf. unfassbar viel Geduld".
Neben den "klassischen" Such- und Sortierproblemen gibt es mit den Optimierungsproblemen eine weitere wichtige Problemklasse. Deren Lösung besteht darin, ein Ergebnis zu finden, dass in Bezug auf eine Zielgröße optimal (maximal bzw. minimal) ist. Beispiele hierfür sind das Kürzeste-Wege-Problem, das Rucksackproblem und das Traveling Salesman Problem (TSP).
In der theoretischen Informatik werden hauptsächlich Entscheidungsprobleme (decision problems) betrachtet. Dies sind Probleme, bei denen die Lösung entweder JA (true) oder NEIN (false) lautet. Beispiel für ein Entscheidungsproblem: "Ist $k$ eine Primzahl?" Die Frage "Ist 123 eine Primzahl?" nennt man eine Instanz dieses Entscheidungsproblems. In der Theorie formaler Sprachen lautet eine zentrale JA-NEIN-Frage: "$w\in L$?" Wir wissen, dass sie nicht für alle Sprachklassen allgemein entscheidbar ist. Für entscheidbare Sprachen gibt es dafür Verfahren unterschiedlicher Effizienz, was sich bei der Verarbeitung von Programmen deutlich auswirkt.
Auf der einen Seite sind Such- und Optimierungsprobleme für die Praxis besonders relevant und auf der anderen Seite sind Entscheidungsprobleme sehr gut erforscht. Dies führt zu der Frage, ob sich die Komplexität eines Optimierungsproblems auf die Komplexität eines zugehörigen Entscheidungsproblems zurückführen lässt. Dies ist in der Tat möglich!
Das zu einem Optimierungsproblem $OP$ gehörende Entscheidungsproblem $EP$ konstruiert man unter Verwendung der Lösung des $OP$. Die Entscheidungsvariante des TSP lautet: "Gibt es eine Rundreise, deren Länge geringer ist als $s$?". $s$ wird also als Schranke $EP$ eingebaut. Nun hat man ein Entscheidungsproblem, das genauso aufwändig ist und das man in der theoretischen Informatik (Komplexitätstheorie und Berechenbarkeitstheorie) betrachten kann.
Die Komplexitätstheorie beschäftigt sich mit dem Aufwand von Problemlösungen. In der Berechenbarkeitstheorie geht es um die algorithmische Lösbarkeit eines Problems. Da für das TSP alle möglichen Städtefolgen durchprobiert werden können, handelt es sich um ein entscheidbares Problem allerdings erfordert dieser Brute-force-Ansatz exponentiellen Zeitaufwand.
Inhaltsverzeichnis |
P und EXP
Definition 13.1 Die Komplexitätsklasse $P$ enthält alle Entscheidungsprobleme, die sich mit einer deterministischen Turing-Maschine (DTM) mit polynomialem Zeitaufwand lösen lassen. Sie liegen in $\mathcal{O}(n^{\mathcal{O}(1)})$.
Wir verwenden hier eine DTM nach der klassischen Definition mit einem endlosen Band aufeinander folgender Felder. (Für praxisbezogene Interpretationen ist eine Mehrbandmaschine besser geeignet.)
Zur Aufwandsbestimmung werden die erforderlichen Arbeitstakte (= Anzahl der Konfigurationenübergänge) der betrachteten DTM "gezählt". Dies ist notwenig, um von den konkreten Gegebenheiten (Messung der Laufzeit eines Verfahrens, das auf einer bestimmten Hardware im Netz ausgeführt wird) zu abstrahieren.
Glücklicherweise fallen sehr viele Probleme in die Kategorie $P$, z.B. das Single Source Shortest Path-Problem oder das Problem des Minimalen Spannbaums.
Definition 13.2 Die Komplexitätsklasse $EXP$ enthält alle Entscheidungsprobleme, die sich mit einer deterministischen Turing-Maschine mit exponentiellem Zeitaufwand lösen lassen. Sie liegen in $\mathcal{O} \left( \mathcal{O}(k)^{n^{\mathcal{O}(1)}} \right)$ mit $k>1$.
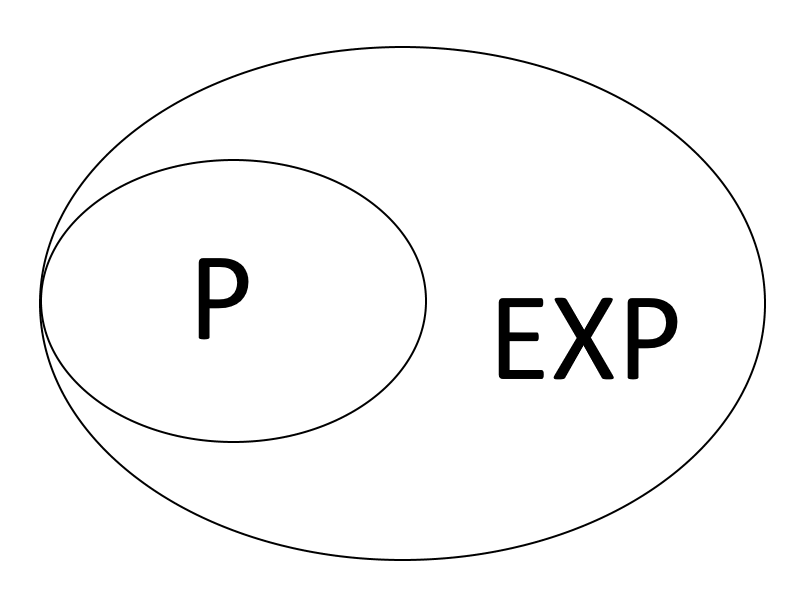
Da jedes Polynom durch eine Exponentialfunktion nach oben beschränkt werden kann, gilt offensichtlich $P \subset EXP$.
Wenn man für ein gegebenes Problem zeigen kann, dass es nur eine exponentielle (nicht polynomiale) untere Schranke für den Zeitaufwand zur Lösung gibt, liegt das Problem in $EXP$ und nicht in $P$.
NP und NEXP
Definition 13.3 Die Komplexitätsklasse $NP$ enthält alle Entscheidungsprobleme, die sich mit einer nichtdeterministischen Turing-Maschine (NTM) mit polynomialem Zeitaufwand (exakt) lösen lassen.
$NP$ steht dabei für nichtdeterministisch polynomial. Eine nichtdeterministische Turing-Maschine (NTM) ist ein Berechenbarkeitsmodell, das "die richtige" Fortsetzung erraten kann. Durch "magische Kräfte" (Orakelvorstellung) ist es in der Lage, falls es eine Entscheidungsmöglichkeit gibt, immer die zu wählen, die im Entscheidungsproblem zur JA-Antwort führt. Findet dieses Raten nur polynomial oft aus polynomial vielen Antwortmöglichkeiten statt, so ist das Problem nichtdeterministisch in Polynomialzeit lösbar, es liegt also in $NP$.
In folgendem Beispiel geht es um das SAT-Problem (satisfiabilty): Für eine aussagenlogische Formel $F$, wie z.B. ${\displaystyle (x_{1}\lor \lnot x_{2})\land (\lnot x_{1}\lor x_{2}\lor x_{3})\land \lnot x_{1}}$ soll festgestellt werden, ob es eine Belegung der Variablen mit $true$ oder $false$ gibt, die $F$ erfüllen, d.h. $wahr$ werden lassen.
Ein Brute-force-Verfahren, das alle Belegungskombinationen betrachtet, liegt auf der Hand:
Es erfordert einen exponentiellen Aufwand in $\mathcal{O}(2^n)$. Warum? Wahrheitswertetabelle für $n=3$ Variablen; ergibt $8=2^n$ Kombinationen.
Man kann zeigen, dass ein Problem in $NP$ liegt, indem man ein nichtdeterministisches Lösungsverfahren, das (nichtdeterministisch) in Polynomialzeit läuft, für dieses Problem angibt. Für die praktische Berechnung bringt das gar keinen Vorteil, da man die Empfehlungen des Orakels deterministisch nachbilden muss. Dort steckt dann der exponentielle Aufwand. Die Zugehörigkeit eines Problems zu $NP$ ist jedoch von theoretischem Interesse, wie wir gleich sehen werden.
Für das SAT-Problem können wir ein nichtdeterministisches Verfahren wie folgt angeben:
Es gibt auch polynomial entscheidbare Varianten des SAT-Problems (Horn-Klausel-Logik). Man benötigt sie in der logischen Programmierung, für die exponentielles Wachstum nicht hinnehmbar wäre.
Für das 0/1-Rucksackproblem kann man folgenden Algorithmus angeben: man rät für jeden der $n$ Gegenstände, ob man ihn in den Rucksack legen soll oder nicht. Da die NTM in der Lage ist, die Antwort immer so zu wählen, dass die Lösung optimal wird (bzw. in Form des Entscheidungsproblems den gegebenen Wert überschreitet oder nicht), funktioniert der Algorithmus. Da das Raten $n$-mal aus 2 Auswahlmöglichkeiten statfindet, handelt es sich um nichtdeterministische Polynomialzeit. Somit ist das 0/1-Rucksackproblem in $NP$.
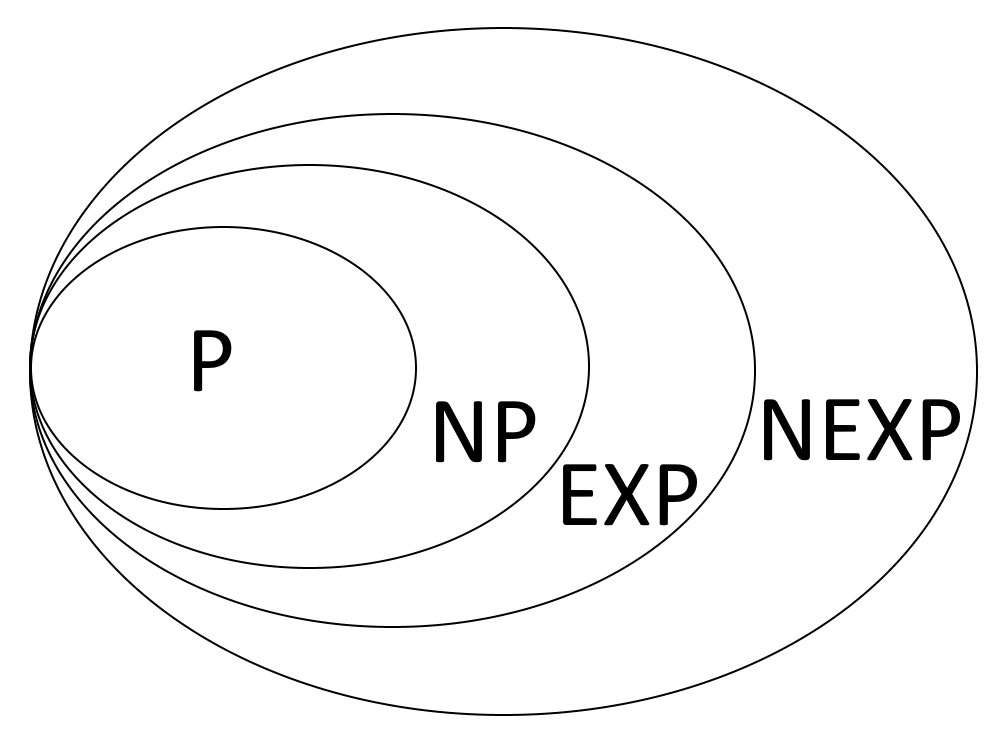
Definition 13.4 Die Komplexitätsklasse $NEXP$ enthält alle Entscheidungsprobleme, die sich mit einer NTM mit exponentiellem Zeitaufwand lösen lassen.
Es ist offensichtlich dass $P$ eine Teilmenge von $NP$ ist: Wenn ein Problem in Polynomialzeit gelöst werden kann, kann man die potenzielle Lösung in Polynomialzeit verifizieren, indem man sie einfach verwendet.
R
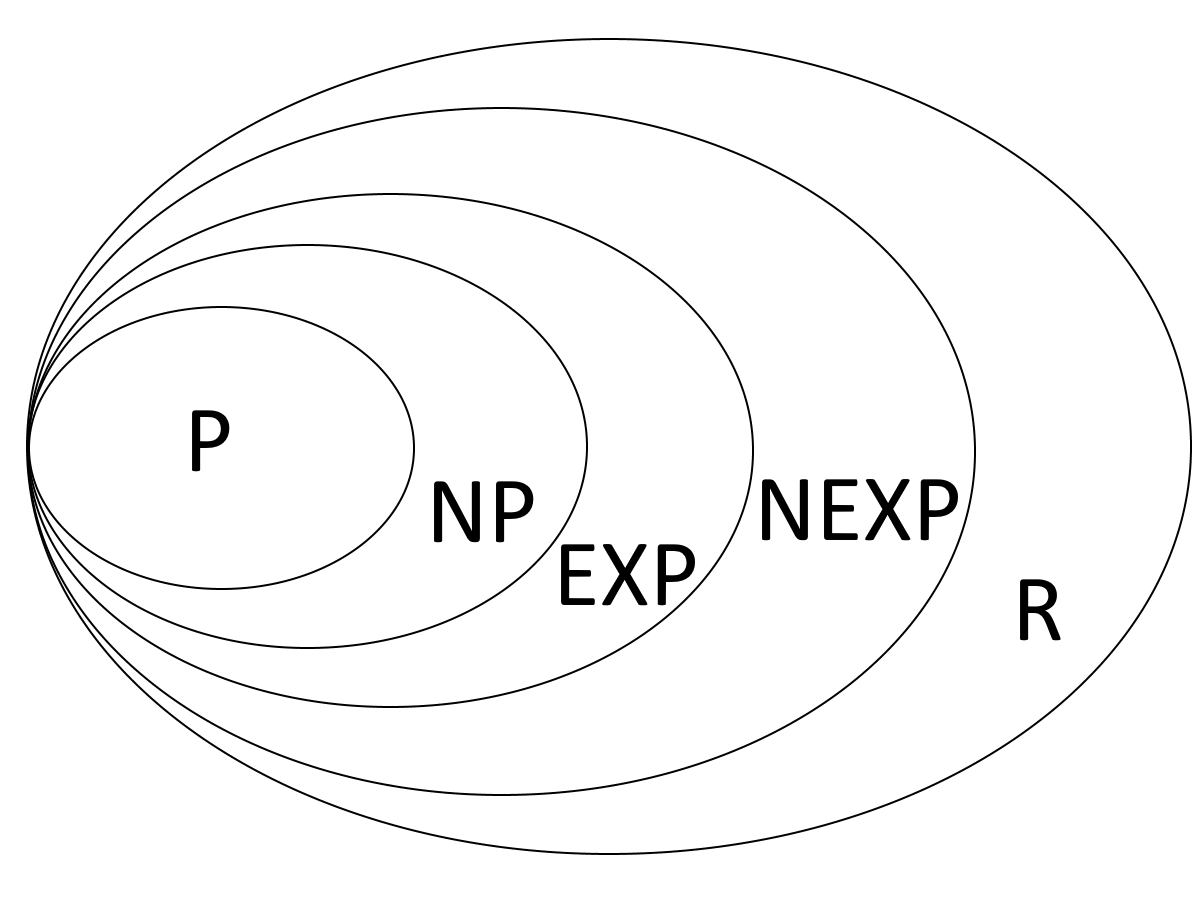
Definition 13.5 Die Komplexitätsklasse $R$ enthält alle Entscheidungsprobleme, die mit einer Turing-Maschine in endlicher Zeit gelöst werden können. Sie stellt die Menge aller entscheidbaren Sprachen (= rekursiven Sprachen; daher das $R$) dar, welche eine echte Teilmenge aller rekursiv aufzählbaren Sprachen $RE$ ist.
$R$ enthält also alle entscheidbaren Probleme, für die die Maschine in jedem Fall stoppt und eine bestimmte Ausgabe (w/f) produziert.
Es gibt in der Tat Probleme, die nicht in $R$ liegen und somit nicht entscheidbar sind.
Ein Beispiel für ein unentscheidbares Problem ist das Halteproblem. Es stellt die Frage nach der Existenz eines Programms, das für ein beliebiges Programm und dessen (passende) Eingaben feststellt, ob es terminiert oder nicht. Ein weiteres unentscheidbares Problem ist das Wortproblem für rekursiv aufzählbare Sprachen (Chomsky-Typ-0-Sprachen). Die exemplarisch genannten Sprachen sind semi-entscheidbar, die für bestimmte Eingaben nicht terminieren.
Polynomiale Reduktion
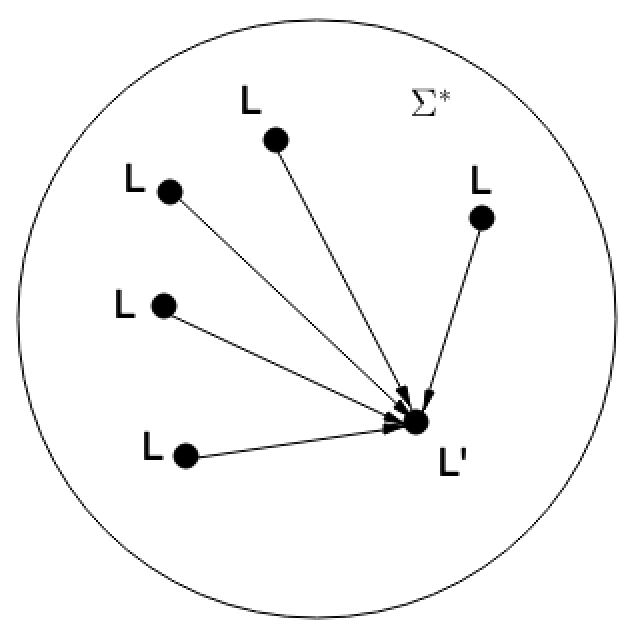
Definition 13.7 Seien $L$ und $L'$ zwei Entscheidungsprobleme mit $L, L' \subset \Sigma^*$. $L$ ist auf die Sprache $L'$ polynomial reduzierbar, wenn es eine totale und in Polynomialzeit berechenbare Funktion $f: \Sigma^* \to \Sigma^*$ gibt, so dass für alle Wörter $w \in \Sigma^*$ gilt: $w \in L \Leftrightarrow f(w) \in L'$. Für die Reduktion von $L$ auf $L'$ schreibt man $L \leq_p L'$.
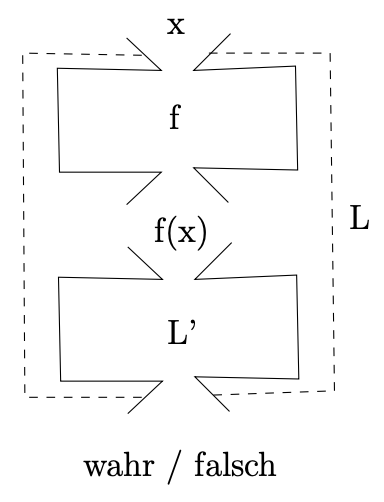
Es ist wichtig, dass die Definition nicht nur für Wörter aus $L$ bzw. $L'$ gilt, sondern alle Wörter aus $\Sigma^*$ betrifft. Dies wird in folgender Abbildung dargestellt.
$f$ kann also nicht frei erfunden werden, sondern wird so gewählt, dass für jedes $x\in\Sigma^*$ auf die Frage $x\in L?$ die gleiche Antwort gegeben wird, wie für $f(x)\in L'?$.
Bei der polynomialen Reduktion $L \leq_p L'$ wird also eine Transformation angegeben, durch die die Lösung eines Problems $L$ auf die Lösung des Problems $L'$ verlagert wird. D.h., jede Probleminstanz von $L$ wird (mittels $f$) in eine von $L'$ "umgerechnet" und gelöst, was einer Lösung von $L$ entspricht.
Liegt die Reduktion $L \leq_p L'$ vor, so kann man sagen:
- $L$ ist im Wesentlichen nicht schwieriger als $L'$.
- $L'$ ist mindestens so schwierig wie $L$.
Mit Hilfe der polynomialen Reduktion kann man ein noch unklassifiziertes Problem $A$ klassifizieren (in $P$ bzw. in $NP$), indem ein passendes Problem $B$ zur Reduktion herangezogen wird:
- Wenn $A \leq_p B$ und $B\in P$, dann ist $A\in P$.
- Wenn $A \leq_p B$ und $B\in NP$, dann ist $A\in NP$.
NP-schwere Probleme (NPH)
Im Folgenden betrachten wir die Klassen $P$ und $NP$. Es geht darum herauszufinden, ob $P=NP$ gilt. Dies würde bedeuten, dass Probleme, die sich mittels Nichtdeterminismus in der oben beschriebenen Weise darstellen lassen, d.h. in $NP$ liegen, deterministisch in Polynomzeit lösbar sind.
Offensichtlich gilt $P\subset NP$, wobei man ganz formal das nichtdeterministische Pendant aus der (in Polynomzeit berechneten) Lösung gewinnt. Ein Orakel "rät" jeweils aus einer Einermenge. Das "Raten" geschieht also nur polynomial oft aus polynomial vielen Antwortmöglichkeiten. Genau dies wird für die Mitgliedschaft in $NP$ verlangt.
Aber wie steht es mit $NP$-Problemen und $P=NP$? Um diese Frage enorm zuzuspitzen, definieren wir unter Verwendung der polynomiale Reduktion zwei weitere Problemklassen, nämlich $NPH$ und $NPC$.
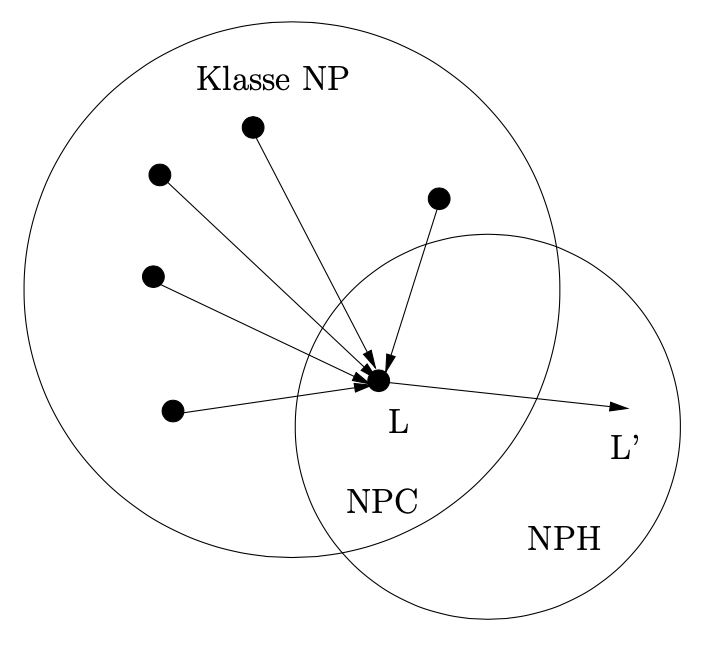
Definition 13.6 Ein Problem ist $NP$-schwer ($NP$-hard, kurz: $NPH$), wenn es mindestens so schwer ist, wie die schwersten Probleme in $NP$. Sei $L′\subseteq\Sigma^*$. $L'$ heißt NP-schwer, wenn gilt: $\forall L\in NP: L\leq_p L'$. (Alle $L$ aus $NP$ sind polynomial reduzierbar auf $L'$.)
Die folgende Abbildung illustriert den Sachverhalt. $L'$ ist nach Def. ein NP-schweres Problem.
NP-Vollständigkeit (NPC)
Definition 13.8 Ein Problem ist $NP$-vollständig ($NP$-complete, kurz: $NPC$), wenn es in $NP$ liegt und $NP$-schwer ist.
Um zu zeigen, dass ein Problem ...
- ... $NP$-vollständig ist, muss man also zeigen, dass es in $NP$ liegt und $NP$-schwer ist.
- ... in $NP$ liegt, reicht es aus einen nichtdeterministischen Polynomialzeit-Algorithmus anzugeben.
- ... $NP$-schwer ist, muss man zeigen, dass sich alle Probleme aus $NP$ auf dieses Problem reduzieren lassen. Das wäre allerdings sehr sehr aufwendig, falls überhaupt erfolgreich: Schließlich gibt es sehr viele Probleme in $NP$.
Deshalb machen wir uns die Tatsache zunutze, dass sich jedes Problem aus $NP$ auf jedes $NP$-vollständige Problem $L$ reduzieren lässt. Gelingt die Reduktion von $L$ auf $L'$, so ist durch die Transitivität der polynomialen Reduktion die $NP$-Schwere von $L'$ bewiesen.
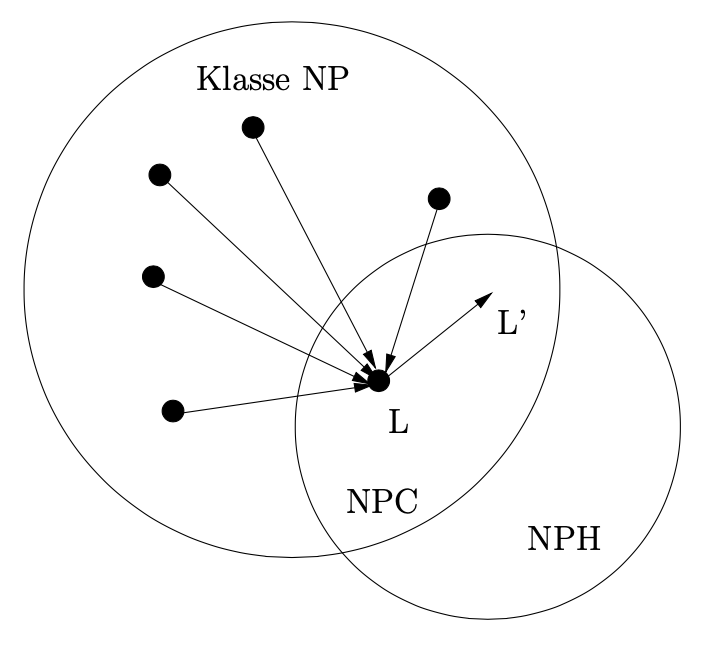
Wenn $L'$ in $NP$ liegt, ist $L'$ nicht nur NP-schwer, sondern sogar ein $NP$-vollständiges Problem, wie die folgende Abbildung zeigt.
- Wenn $L$ NP-schwer ist und $L \leq_p L'$, dann ist $L′$ NP-schwer.
- Wenn $L$ NP-vollständig ist, $L \leq_p L'$ und $L'$ in NP, dann ist $L′$ NP-vollständig.
Zum Nachweis immer neuer $NP$-vollständiger Probleme $L'$ ist also prinzipiell nur ein einziges bekanntes $NP$-vollständiges Problem $L$ erforderlich. Man nimmt im Allgemeinen das $L$, das am besten zu $L'$ passt.
In der folgenden Abb. werden die Komplexitätsklassen $P$, $NP$, $NPC$, $NPH$ und $EXP$ (identisch mit $EXPTIME$) unter der Annahme $P \neq NP$ zusammengestellt.
Eine Zusammenstellung als "Complexity Zoo" zeigt, welche derartige Klassen definiert und bereits untersucht wurden.
Satz von Cook (1971): Das Henne-und-Ei-Problem
Für ein $NP$-Problem $L'$ lässt sich mittels polynomialer Reduktion eines $NP$-vollständigen Problems $L$ auf $L'$ zeigen, dass $L'$ $NP$-vollständig ist. Doch wie hat das angefangen als es noch kein einziges $NP$-vollständiges Problem $L$ gab?
Satz von Cook: Das Erfüllbarkeitsproblem der Aussagenlogik (SAT-Problem) ist $NP$-vollständig.
Die $NP$-Vollständigkeit des "ersten" $NP$-vollständigen Problems (SAT) wurde von Stephen Cook auf eine andere, sehr aufwändige Art und Weise nachgewiesen. Die Bedeutung des Cook'schen Beweises für die Komplexitätstheorie ist mit der Cantor'schen Diagonalisierung in der Berechenbarkeitstheorie zu vergleichen.
Die Beweisidee beruht darauf, dass jedes Merkmal einer Turing-Maschine als aussagenlogische Formel interpretiert wird.
Da man nun das "erste" $NP$-vollständige Problem gefunden hat, kann man von diesem aus per polynomialer Reduktion die $NP$-Vollständigkeit entsprechender Probleme nachweisen usw.
P vs. NP Problem
Das $P-NP$-Problem ist das wohl bedeutsamste ungelöste Problem in der Informatik. Es stellt die Frage, ob $P = NP$ oder $P \neq NP$ gilt, d.h. ob $P$ und $NP$ die gleichen Mengen sind, oder ob es Probleme gibt, die in $NP$ liegen, aber nicht in $P$.
Satz 13.1 Wenn $A$ ein $NP$-vollständiges Problem ist, dann gilt: $A\in P\Leftrightarrow P=NP$.
Man kann zeigen, dass die Menge $NP \setminus (NPC \cup P)$ unter der Annahme $P \neq NP$ nicht leer ist. Das Primzahlproblem ist vermutlich weder in $P$ noch $NP$-vollständig ($NPC$). Niemand weiß dies wirklich.
Die Komplexitätstheorie hat also für eine enorme Zuspitzung der Frage nach der Existenz von Polynomialzeitalgorithmen gesorgt, für Probleme, die (vermutlich) nicht effizient gelöst werden können. Die Tatsache, dass es trotz enormer Anstrengungen bis heute niemanden gelungen ist, auch nur ein einziges solche $NP$-vollständiges Problem in Polynomialzeit zu lösen, stützt die Vermutung, dass es keine Polynomialzeit-Lösungen für alle $NP$-Probleme gibt.
Bewiesen ist dies allerdings noch nicht. Dass es noch niemandem gelungen ist, einen Polynomialzeitalgorithmus für ein $NP$-vollständiges Problem anzugeben, heißt nicht, dass es keinen geben kann. Würde es gelingen, für ein einziges $NP$-vollständiges Problem $A$ einen Polynomialzeitalgorithmus anzugeben, so würde daraus $P = NP$ folgen, da man jedes Problem aus $NP$ auf das Problem $A$ reduzieren könnte, und dank dieses neuen Algorithmus' in Polynomialzeit lösen könnte. Dies würde jedes Problem aus $NP$ automatisch zu einem Problem in $P$ machen.
Gelänge andererseits für ein einziges $NP$-vollständiges Problem der Nachweis, dass die untere Schranke für den Berechnungsaufwand in $\Omega(\Theta(1)^n)$ liegt, so hätte man ein Problem gefunden, dass nachweislich in $NP$ liegt, aber nicht in $P$ und es wäre nachgewiesen, dass die Mengen $P$ und $NP$ nicht gleich sind. Wir wüssten dann, dass $P \neq NP$ bzw. $P \subsetneq NP$. Die Befunde legen nahe, dass dies so ist, einen Beweis ergeben sie nicht.
Beispiele für NP-vollständige Probleme
Karps 21 NP-vollständige Probleme
SAT Problem
Beim SAT-Problem, auch Boolean satisfiability problem genannt, geht es um die Frage nach der Erfüllbarkeit eines aussagenlogischen Ausdrucks in konjunktiver Normalform. Klauseln sind Disjunktionen von Literalen (negierten und unnegierten Variablen) der Form $(x_1\lor x_2\lor\ldots\lor x_k), k\leq n$. Diese Klauseln werden mittels "$\land$" verknüpft. In folgendem Beispiel ist $n=3$. $$ (x_1 \lor x_2) \land \overline{x_3} \land \overline{x_1} $$ Die Frage ist nun nach einer Belegung der in der Formel vorkommenden Variablen (jeweils entweder mit $0$ oder $1$), sodass der gesamte Ausdruck wahr ($1$) wird. Die aussagenlogische Formel im Beispiel ist mit der Belegung $x_1 = 0, x_2 = 1, x_3 = 0$ erfüllbar. Hingegen ist $$ (x_1 \lor x_2) \land x_3 \land \overline{x_2} \land (\overline{x_1} \lor \overline{x_3}) $$ nicht erfüllbar.
Ein deterministisches Lösungsverfahren erfordert eine Tabelle für alle möglichen Belegungen der $n$ Variablen. Dies sind $2^n$ Stück. Eine Baumdarstellung unterstreicht optisch den exponentiellen Lösungsaufwand. Unter Nutzung des Nichtdeterminismus hingegen muss $n$-mal "geraten" werden, für jede vorkommende Variable $x_1,x_2,\ldots,x_n$ genau einmal: entweder $0$ oder $1$. Für die so gewählte Belegung kann in Polynomzeit festgestellt werden, ob der Wert des gesamten Ausdrucks $1$ ist oder nicht. Somit liegt das Problem in $NP$.
Das $n$-SAT-Problem für $n\leq 2$ liegt in $P$ und für $n\geq 3$ ist es $NP$-vollständig. Das macht insbesondere das $3$-SAT-Problem so interessant.
3-SAT Problem
Beim 3-SAT Problem geht es wie beim SAT Problem um die Erfüllbarkeit einer aussagenlogischen Formel. Jedoch handelt es sich um eine aussagenlogische Formel, die in konjunktiver Normalform (CNF) mit maximal 3 Literalen (3CNF) vorliegt.
Ein Beispiel für einen solchen Ausdruck mit $n=4$:
$$ (\overline{x_1} \lor x_2 \lor x_3) \land (x_2 \lor \overline{x_3} \lor x_4) \land (x_1 \lor \overline{x_2}) $$
Die geklammerten Ausdrücke, wie $(\overline{x_1} \lor x_2 \lor x_3)$, werden Klauseln (clauses) genannt. Die negierten und nichtnegierten Variablen stehen für die Literale, so wie weiter oben bereits ausgeführt wurde.
Nun stellt sich die Frage, wie man zeigt, dass das 3SAT-Problem $NP$-vollständig ist, genauer wie man von einem $NP$-vollständigen Problem auf das 3SAT-Problem reduziert. Da das SAT-Problem dem 3SAT-Problem sehr ähnlich ist, ist offensichtlich, dass dieses Problem als Ausgangspunkt für die polynomielle Reduktion geeignet ist: $SAT\leq_p 3SAT$.
Man muss also einen Weg finden, eine beliebige aussagenlogische Formel in die konjunktive Normalform mit maximal 3 Literalen bringen. Dafür muss man zunächst die aussagenlogische Formel in konjunktive Normalform bringen. Hierfür werden die De Morgan'schen Regeln und das Distributivgesetz angewandt. Zunächst werden alle Negationen in die Negationsnormalform gebracht, dafür werden folgende Umformungen vorgenommen:
$$ \begin{align*} \overline{P \lor Q} & \rightarrow \overline{P} \land \overline{Q} \\ \overline{P \land Q} & \rightarrow \overline{P} \lor \overline{Q} \end{align*} $$
Anschließend wird das Distributivgesetz angewandt, bis nur noch Konjunktion (und-Verknüpfungen) über Disjunktionen (oder-Verknüpfungen) vorliegen.
$$ P \lor (Q \land R) \rightarrow (P \lor Q) \land (P \lor R) $$
Nun muss sichergestellt werden, dass sich in jeder Klausel maximal 3 Literale befinden. Hierfür muss man einen Weg finden, eine Klausel mit mehr als 3 Literalen in einen Ausdruck, der maximal 3 Literale pro Klausel und die gleiche Entscheidbarkeit besitzt, umzuformen.
Hat man beispielsweise die Klausel $(x_1 \lor x_2 \lor x_3 \lor x_4 \lor x_5)$, so kann man durch Hinzufügen zusätzlicher Variablen den Ausdruck umformen. Die Regel lautet, dass die Entscheidbarkeit von $(x_ 1 \lor x_2 \lor A)$ die gleiche ist, wie die von $(x_1 \lor x_2 \lor y_1) \land (\overline{y_1} \lor A)$. Es handelt sich jetzt nicht mehr um eine äquivalente aussagenlogische Formel, da eine neue Variable eingefügt wurde, jedoch bleibt die Entscheidbarkeit die gleiche. $(x_1 \lor x_2 \lor x_3 \lor x_4 \lor x_5)$ würde man schrittweise zu 3 Klauseln umformen, allgemein gesagt zu $n-2$ Klauseln.
$$ (x_1 \lor x_2 \lor x_3 \lor x_4 \lor x_5) $$ $$ (x_1 \lor x_2 \lor y_1) \land (\overline{y_1} \lor x_3 \lor x_4 \lor x_5) $$ $$ (x_1 \lor x_2 \lor y_1) \land (\overline{y_1} \lor x_3 \lor y_2) \land (\overline{y_2} \lor x_4 \lor x_5) $$
Die aussagenlogische Formel ist nun in 3CNF-Form und damit gültige Eingabe für das 3-SAT Problem.
Damit wurde eine Reduktion vom SAT-Problem auf das 3-SAT Problem angegeben. Daraus folgt, dass das 3-SAT Problem $NP$-schwer ist. Da man für jede der $n$ Variablen raten kann, ob sie wahr oder falsch sein soll, liegt das Problem in $NP$ und ist somit $NP$-vollständig.
Cliquenproblem
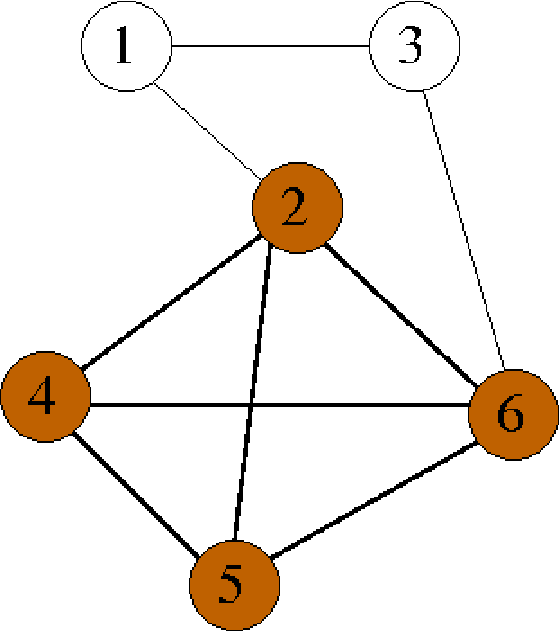
Beim Cliquenproblem wird gefragt, ob ein (einfacher) Graph mindestens $n$ Knoten besitzt, die alle untereinander verbunden sind. (Eine Clique ist also eine Teilmenge von Knoten, bei denen jeder mit jedem verbunden ist.)
Das Optimierungsproblem fragt nach der größten Clique im Graphen. Das Entscheidungsproblem fragt, ob es im Graphen eine Clique gibt, die mindestens $n$ groß ist.
Beispiel für eine Clique der Größe 4
Für das Problem kann auf einer deterministischen Maschine folgender Backtracking Algorithmus angegeben werden. Dabei wird das Problem mit Hinzufügen des Knotens zur Clique und ohne Hinzufügen des Knotens rekursiv aufgerufen. Das zahlenmäßig größere Ergebnis der beiden Berechnungen, wird in der Rekursionsebene darüber zurückgegeben.
Es ist leicht zu zeigen, dass dieses Problem in $NP$ ist, schließlich kann man bei jedem Knoten raten, ob er zu einer Clique gehört, welche mindestens $n$ Knoten enthält.
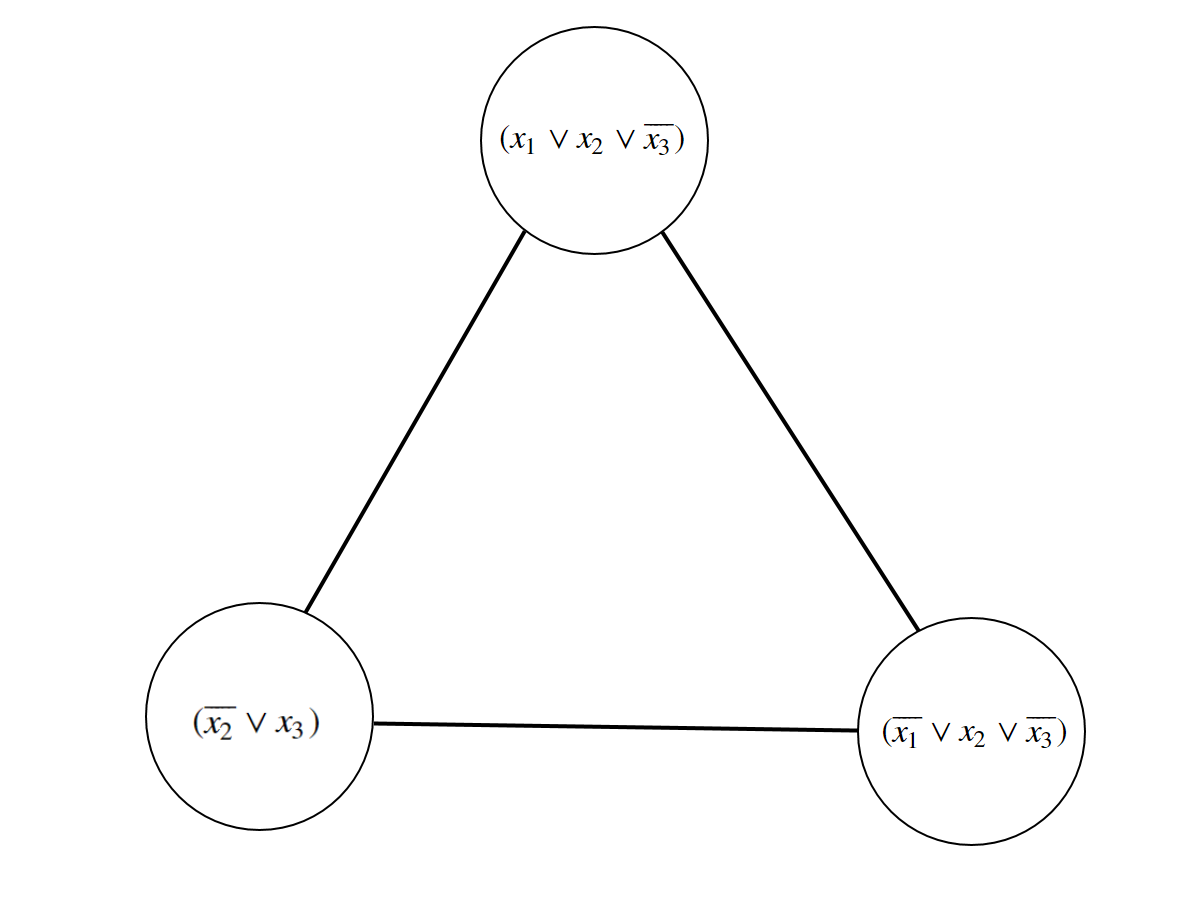
Die $NP$-Schwere kann durch Reduktion des 3SAT-Problems gezeigt werden. Beim 3SAT-Problem ist es erfüllt, wenn jede der Klauseln wahr ist. Das Cliquenproblem ist erfüllt, wenn es eine Clique gibt, die mindestens die Größe $n$ hat. Dies kann man übertragen, indem man zunächst einen Graphen mit $k$ Knoten erstellt, bei dem jeder Knoten mit jedem verbunden ist. $k$ entspricht dabei die Anzahl der Klauseln.
Beispiel
$$ (x_1 \lor x_2 \lor \overline{x_3}) \land (\overline{x_2} \lor x_3) \land (\overline{x_1} \lor x_2 \lor \overline{x_3}) $$
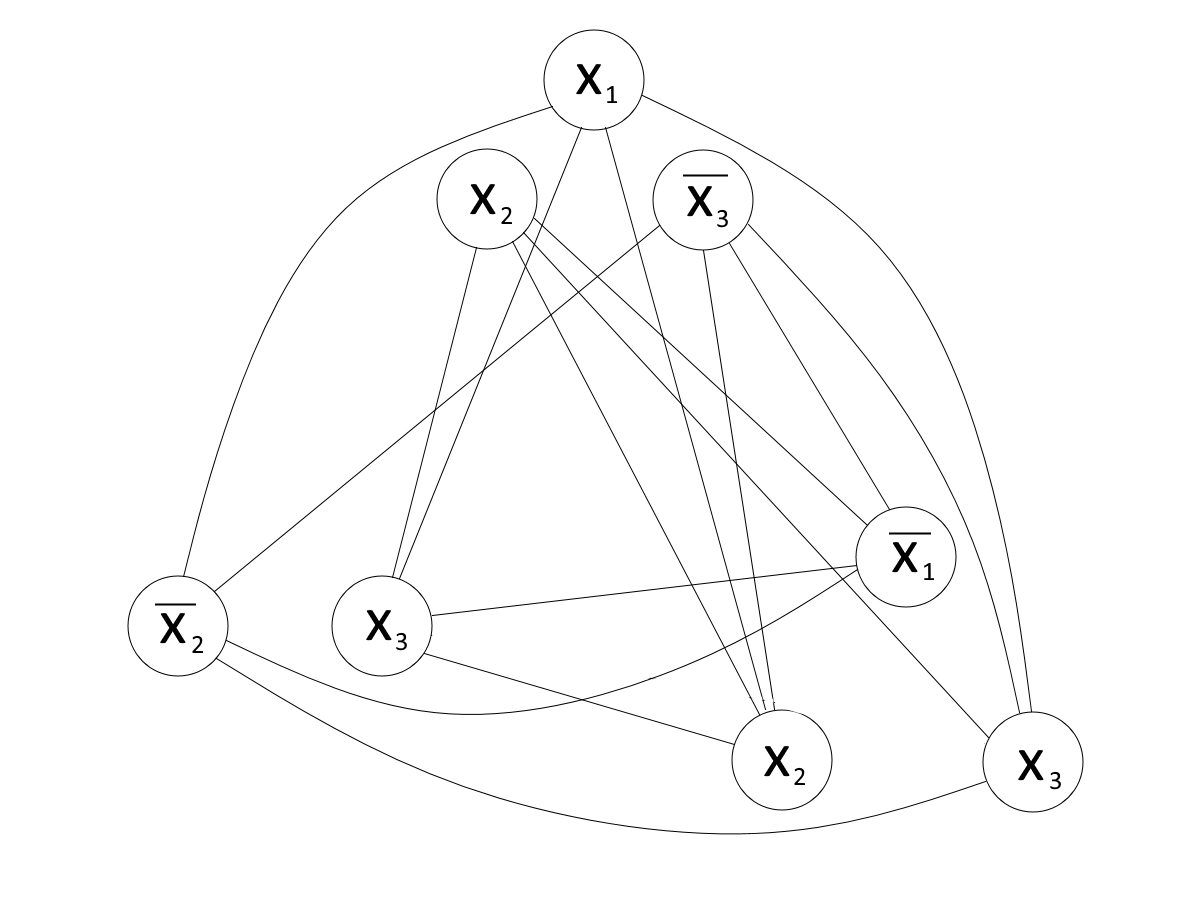
Nun muss man die Knoten, die Klauseln darstellen, durch die bis zu 3 Variablen ersetzen. Dies geschieht, indem man den einen Knoten durch 3 ersetzt und Kanten zu allen Variablen aus anderen Klauseln schafft. Allerdings darf die Kante nur gesetzt werden, wenn die beiden verbundenen Variablen so in der Kombination auftreten können. Dies ist bei $x_i$ und $\overline{x_i}$ nicht der Fall. Eine Variable kann nicht gleichzeitig wahr und falsch sein. Alle anderen Kombination sind möglich, auch eine Verbindung zwischen $x_i$ und $x_i$ bzw. $\overline{x_i}$ und $\overline{x_i}$, schließlich nehmen die Variablen in beiden Fällen den gleichen Wert an.
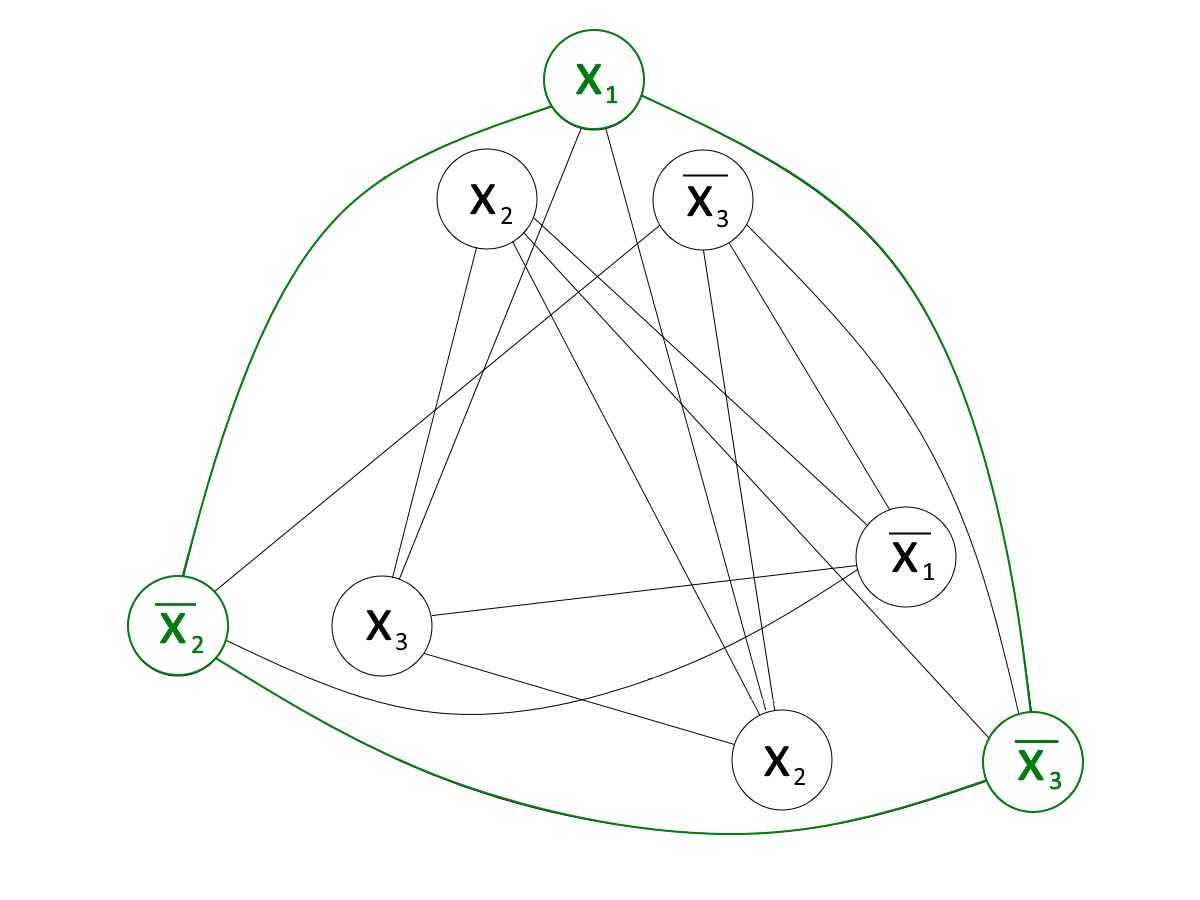
Gesucht ist nun eine Clique der Größe $n$, d.h. der Anzahl der Klauseln, hier $n=3$.
Somit ist die Formel beispielsweise für $x_1 = 1, x_2 = 0, x_3 = 0$ erfüllt.
Wir haben ein Verfahren angegeben, um das 3SAT-Problem in Polynomialzeit auf das Cliquenproblem zu reduzieren. Das Cliquenproblem ist damit $NP$-vollständig.
Independent Set
Independent Set (stabile Menge) ist ebenfalls ein Problem aus der Graphentheorie. Eine Menge von Knoten ist eine stabile Menge, wenn sie untereinander nicht adjazent (benachbart) sind, d.h. nicht durch jeweils eine Kante miteinander verbunden sind. Daraus ergibt sich auch die Benennung co-Clique. Beim Optimierungsproblem wird nach der größten stabilen Menge in einem Graphen gesucht. Beim Entscheidungsproblem wird die Frage gestellt, ob es eine stabile Menge mit mindestens $k$ Knoten im Graphen gibt.
Beispiel
Vergleicht man dieses Problem mit dem Cliquenproblem, so stellt man eine gewisse Ähnlichkeit fest. Beim Cliquenproblem ist eine Menge von Knoten gesucht, die benachbart und alle Kanten zwischen ihnen vorhanden sind. Beim Independent-Set-Problem ist eine Menge von Knoten gesucht, die gar keine Kanten untereinander haben.
Diese Erkenntnis kann genutzt werden, um eine Reduktion des Cliquenproblems auf das Independent Set zu konstruieren. Dafür werden beim Graphen überall dort, wo sich Kanten befinden, die Kanten entfernt und überall dort, wo sich zwischen zwei Knoten keine Kanten befanden, werden Kanten eingefügt. Nun löst man dieses Problem mit einem Algorithmus für Independent Set und erhält für das Optimierungsproblem die gleiche Menge an Knoten und für das Entscheidungsproblem die gleiche Antwort.
Beispiel
Cliquenproblem
Independent Set
Da das Independent Set-Problem in $NP$ liegt, ist das Problem $NP$-vollständig.
Man kann die Reduktion auch andersherum von Independent Set zum Cliquenproblem auf die gleiche Art und Weise definieren. Man muss lediglich dort Kanten setzen wo keine waren, und dort Kanten entfernen, wo welche waren. Im folgenden Beispiel wird Independent Set auf das Cliquenproblem reduziert und mit der bereits oben definierten Funktion gelöst.