Hash Tables und Assoziative Listen WS13-14

Aus ProgrammingWiki

Autoren: Daniel Franke, Jens Klinger

Wörterbuchproblem

In diesem Wiki befassen wir uns mit der Suche nach bereits gespeicherten Daten. Wir nehmen an, dass jeder Eintrag durch einen Schlüssel eindeutig identifiziert wird. Wichtig ist dabei insbesondere, dass eine Ordnung auf den Schlüssel definiert ist (z.B. die alphabetische Ordnung in einem Wörterbuch).

Das Wörterbuchproblem kann wir folgt beschrieben werden:

Gegeben: Menge von Objekten (Daten) die über einen eindeutigen Schlüssel (z.B. ganze Zahl, String) identifiziert sind.

Gesucht: Struktur zur Speicherung der Objektmenge, so dass mindestens die folgenden Operationen (Methoden) effizient ausführbar sind:

• Search (Wiederfinden, Zugreifen)
• Insert
• Delete

Es ist zu beachten das folgende Bedingungen die Wahl der Lösung des Wörterbuchproblems beeinflussen können:

• Häufigkeit der Operationen:

1. überwiegend Suchen (statisches Verhalten)
2. überwiegend Einfügen und Löschen (dynamisches Verhalten)
3. annähernde Gleichverteilung der Operationen
4. keine Verteilung bekannt

• Weitere zu implementierende Operationen

1. Durchlaufen der Menge in bestimmter Reihenfolge (z.B. nach Schlüsselwert aufsteigend sortiert)
2. Mengen-Operationen: Vereinigung, Durchschnitt, Differenz, ...

In den folgenden Abschnitten wird Anhand von assoziativen Listen bzw. Arrays und Hash-Tables gezeigt, wie Ansätze zur Lösung des Wörterbuchproblems implementiert werden können.

Assoziative Arrays

Arrays

Ein Array in seiner einfachsten Form ähnelt einer Tabelle mit mehreren Spalten und nur einer Zeile:

Assoziative Arrays

Intuitiv und lesbar werden Arrays, wenn die einzelnen Felder unterschiedliche Datentypen enthalten und statt des numerischen Index ein Schlüssel verwendet wird.

Assoziative Arrays benutzen Zeichenketten statt Zahlen als Index. Das macht den Code leichter lesbar und weniger fehleranfällig. Es handelt sich um einfache Schlüssel-Wert-Paare. Diese sind sinnvoll, wenn die Elemente des Arrays verschiedene Datentypen haben und nicht sortiert werden müssen.

Merkmale

• Datenstruktur, die nichtnumerische Schlüssel (meist Zeichenketten) verwendet, um enthaltene Elemente zu adressieren.
• Schlüssel-Wert-Paar
• Keine festgelegte Reihenfolge
• Schlüssel werden idealerweise so gewählt, dass eine nachvollziehbare Verbindung zwischen Schlüssel und Datenwert besteht
• Implementierung, üblicherweise, mittels Hash-Tables

Für die Arbeit mit assoziativen Arrays werden drei Methoden benötigt: Insert, Search, Delete.

Insert(key, value) {
  list[key] = value;
}

Search(key) {
  return list[key];
}

Delete(key) {
  list[key] = null;
}

Diese drei Methoden haben den Vorteil, dass sie in $\mathcal{O}\left( 1\right)$ arbeiten.

Hinweis

In der Programmiersprache C gibt es den Datentyp String nicht. Aus diesem Grund musste man dafür ein Array des Datentyps char wählen. War zum Zeitpunkt der Definition des Arrays nicht bekannt, wie viele Zeichen genau der zu speichernde String haben wird, musste ein möglichst großes Array erzeugt werden. Im schlechtesten Fall jedoch wurde die Größe nicht ausgeschöpft. Dieses Verhalten ist in heutigen Programmiersprachen nicht mehr vorhanden, da diese meist Arrays verwenden, die intern als Hash-Table bzw. Hash-Map realisiert sind.

Hash-Tables

Motivation

Die assoziativen Listen bringen viele Vorteile für die Speicherung von Schlüssel-Wert-Paaren. Jedoch müssen wir hier beachten, dass es im Extremfall so weit kommt, dass nicht alle Daten, die wir speichern wollen, speicherbar sind. Dies wäre bspw. bei einer großen Anzahl von möglichen Schlüsseln der Fall. Zusätzlich kann noch hinzu kommen, dass wir gar nicht alle uns zur Verfügung stehenden Schlüssel benötigen. In diesem Fall würden wir sehr viel Speicherplatz verschwenden.

Diese negativen Punkte wollen Hash-Tables beheben und zugleich auch noch die positiven Eigenschaften von assoziativen Listen übernehmen. Im Gegensatz zu assoziativen Listen verwenden Hash-Tables mathematische Funktionen, um die Position der zu speichernden Daten in einer Tabelle zu ermitteln. Das Wort "Hashing" bedeutet auf deutsch "zerhacken" oder "durcheinander mischen". Dies bringt die Motivation für Hash-Tables sehr gut zum Ausdruck. Die zu speichernden Schlüssel werden durcheinander gemischt und so können die einzelnen Schlüssel-Wert-Paare auf kleinerem Raum (bei vorgegebener maximaler Größe der Tabelle) als bei assoziativen Listen gespeichert werden.

Charakterisierung von Hash-Tables

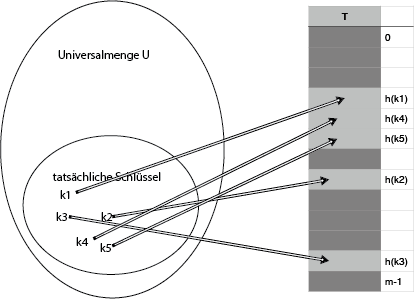
Eine Hash-Table $T$ hat eine Größe $m$. Die Universalmenge $U$ stellt alle potenziellen Schlüssel dar. Die Hashfunktion $h$ berechnet aus dem Schlüssel $k \in U$ des Elementes $e$ den Hashwert $h\left( k\right)$. Dieser wird dann verwendet, um das Schlüssel-Wert-Paar in der Hash-Table abzulegen. Die Position (Bucket) entspricht dabei $h\left( k\right)$ und liegt im Bereich $\left[ 0 \dots m\right]$. Die Einordnung lässt sich so ausdrücken:

\[ h:U \rightarrow \left\{ 0,1, \dots , m-1 \right\} \]

Hat die Hash-Table $T$ eine Größe von $m$ und werden darin $n$ Schlüssel-Wert-Paare gespeichert, so ergibt sich der Füllgrad der Hash-Table $\alpha$ aus dem Verhältnis von $n$ zu $m$. Optimal wäre, wenn für jeden Eintrag $T\left[ h\left( k\right) \right]$ der Hash-Table maximal ein Schlüssel-Wert-Paar gespeichert würde. Damit ergäbe sich ein Füllgrad $\alpha = \frac{n}{m} \leq 1$ und die drei Funktionen (insert, search, delete) hätten einen Aufwand, der in $\mathcal{O}\left( 1\right)$ liegt. In der Praxis wird die Größe der Hash-Table meist so gewählt, dass der Füllgrad bei 0,7 bis 0,8 liegt.

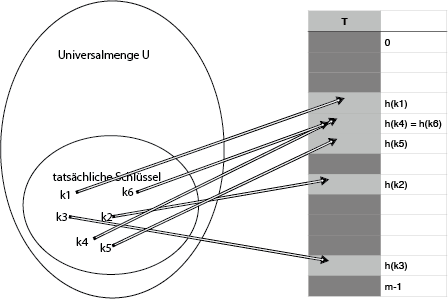
Kollisionen

Spätestens, wenn der Füllgrad $\alpha > 1$ ist, werden mehrere mehrere Schlüssel-Wert-Paare auf einem Platz abgebildet. In diesem Fall kommt es zu einer Kollision. Aus diesem Grund müssen wir eine möglichst gute Hashfunktion wählen, die die Anzahl an Kollisionen auf ein Minimum reduziert.

Eine Hashtabelle ohne Kollision

Eine Hashtabelle mit Kollision

Hashfunktionen

Durch die Verwendung von Hashfunktionen muss gewährleistet sein, dass diese deterministisch sind, das heißt, bei gleicher Werteingabe müssen wir auch immer dasselbe Ergebnis erhalten können.

Eine einfache Möglichkeit der Verwendung einer Funktion für das Hashen ist die Annahme, dass die Schlüssel reelle Zufallszahlen sind und sich gleichmäßig im Bereich $\left[ 0 \dots 1\right]$ verteilen. In diesem Fall können wir die Funktion

\[ h\left( k\right) = \lfloor k\cdot m\rfloor \]

verwenden. Bei den meisten Hashfunktionen wird vorausgesetzt, dass die Schlüssel natürliche Zahlen sind. Ist dies nicht der Fall, kann man anhand diverser Methoden (z. B. anhand der ASCII-Tabelle) die Schlüssel in natürliche Zahlen umrechnen.

Divisionsmethode

Eine weitere Methode zum Berechnen der Schlüssel für die Hash-Table ist die Verwendung der Divisionsmethode. Diese ist recht schnell, da nur eine einzige Division pro Schlüsselberechnung notwendig ist. Der neue Schlüssel ergibt sich dabei als Rest der ganzzahligen Division des ursprünglichen Schlüssels $k$ mit der Größe $m$ der Hash-Table.

\[ h\left( k\right) = k\bmod m \]

Zu beachten ist dabei, dass $m$ keine Potenz von 2 sein sollte und möglichst eine Primzahl ist.

Multiplikationsmethode

Die Multiplikationsmethode besteht bereits aus mehreren Berechnungen. Der Schlüssel $k$ wird dabei mit einer Konstante $A$ multipliziert, die im Bereich $\left[ 0 \dots 1\right]$ angesiedelt ist. Von diesem Produkt werden die Nachkommastellen verwendet, um diese dann mit der Größe $m$ der Hash-Table zu multiplizieren. Der neue Schlüssel ist dann das abgerundete Ergebnis dieser Multiplikation.

\[ h\left( k\right) = \left\lfloor m\cdot \left( k\cdot A−\left\lfloor k\cdot A\right\rfloor \right) \right\rfloor \]

Kollisionsbehandlung

Sobald mehr als ein Element denselben berechneten Schlüssel haben, kommt es zu einer Kollision. Auf dem Platz steht dann bereits ein Element. Diese Kollision muss aufgelöst werden, da sonst die bereits existierenden Daten überschrieben oder die neuen Daten verworfen würden.

Verkettung

Eine Möglichkeit der Kollisionsauflösung ist die Verwendung von verketteten Listen. Dabei werden die Elemente mit demselben berechneten Hashwert in einer verketteten Liste gespeichert. Der Platz in der Hash-Table enthält dann einen Zeiger, der auf den Kopf der verketteten Liste zeigt.

Das Einfügen ist sehr schnell ($\mathcal{O}\left( 1\right)$), wenn man voraussetzt, dass entweder doppelte Elemente zugelassen werden oder es generell keine doppelten Elemente gibt. Sollen doppelte Elemente erkannt werden, hat dies natürlich auch Einfluss auf auf die Laufzeit.

Die Laufzeit, um ein Element in der Liste zu suchen, kann im schlechtesten Fall proportional zur Länge der Liste ($\mathcal{O}\left( n\right)$) sein.

Das Löschen eines Elementes ist bei der Verwendung einer doppelt verketteten Liste ähnlich dem des Suchens, da vor dem Löschen noch der Nachfolger ermittelt werden muss.

Im Worst Case haben alle $n$ Elemente der Hash-Table denselben berechneten Hashwert, so dass sie alle in einer einzigen verketteten Liste liegen. In diesem Fall sollte eine bessere Hashfunktion gewählt werden, die dieses Szenario verhindert.

Offene Adressierung

Bei der offenen Adressierung werden alle Elemente in der Hash-Table gespeichert. Durch die Vermeidung von Zeigern auf Listen, wie sie bei der Verkettung angelegt werden, wird der Belegungsfaktor einer solchen Hash-Table nie größer als 1. Bei Kollisionen wird auf alternative Plätze ausgewichen. Um die Effizienz zu steigern, werden die zu prüfenden Plätze in Abhängigkeit des jeweiligen Schlüssels berechnet. Dieses Verfahren nennt man Sondierung. Es wird so lange wiederholt, bis ein leerer Platz gefunden ist.

Dazu wird die Hashfunktion um einen weiteren Parameter - die Sondierungszahl - erweitert. Daraus ergibt sich dann die Sondierungssequenz.

Das Einfügen in die Hashtabelle stellt kein Problem dar und erfolgt nach den oben genannten Prinzipien. Bei der Suche erfolgt dieselbe Sondierung wie beim Einfügen. Lediglich das Löschen bringt Probleme mit sich. Ein direktes Löschen ist nicht möglich, da sonst Informationen über die Nachfolgeelemente verloren gehen würden. In einem Fall des Löschens werden deshalb entsprechende Einträge mit einem Schlüsselwort als DELETED markiert. Beim Einfügen wird dieses Wort als "leer" betrachtet und kann mit einem neuen Wert überschrieben werden. Beim Suchen allerdings wird es als "beschrieben" betrachtet und stört die Abarbeitung der Sequenz nicht. Sollen Einträge aus der Hashtabelle gelöscht werden, wählt man stattdessen eher die Verkettung.

In der Praxis werden vor allem drei Methoden zur Erzeugung der Sondierungssequenzen genutzt: lineares Sondieren, quadaratisches Sondieren und doppeltes Hashing. Dafür wird eine Hilfshashfunktion $h'(k)$ verwendet.

Lineares Sondieren

Die eigentliche Hashfunktion beim Linearen Sondieren lautet

\[ h\left( k, i\right) = \left( h'\left( k\right) + i\right) \bmod m\].

Der erste Platz wird dann als $T\left[ h'\left( k\right) \right]$ berechnet, danach folgen die nächsten Plätze $T\left[ h'\left( k\right) +1\right]$, $T\left[ h'\left( k\right) +2\right]$, usw. bis $T\left[ m-1\right]$. Hier beginnt die Suche wieder vorn bei $T\left[ 0\right]$, $T\left[ 1\right]$, usw. bis hin zu $T\left[ h'\left( k\right) -1\right]$.

Bei diesem Verfahren gibt es maximal $m$ Sondierungssequenzen.

Quadratisches Sondieren

Das Quadratische Sondieren ist eine Verbesserung des Linearen Sondierens. Die Hashfunktion wird auf

\[ h\left( k, i\right) = \left( h'\left( k\right) + \left( -1\right)^{i+1}\cdot \left\lceil\frac{i}{2}\right\rceil^2 \right) \bmod m\]

geändert.

Hier ist der erste Platz an der Stelle $T\left[ h'\left( k\right)+1 \right]$, die weiteren Plätze sind jedoch danach um einen von $i^2$ abhängigen Betrag verschoben.

Doppeltes Hashing

Beim Doppelten Hashing werden nun zwei Hilfshashfunktionen $h_1\left( k\right)$ und $h_2\left( k\right)$ verwendet. Als Hashfunktion ergibt sich dann

\[ h\left( k, i\right) = \left( h_1\left( k\right) + h_2\left( k\right) \cdot i \right) \bmod m\].

Der erste Platz ergibt sich nun wiederum an $T\left[ h_1\left( k\right) \right]$ und die weiteren Plätze sind um $h_2\left( k\right) \bmod m$ verschoben.

Damit die komplette Hash-Table ausgenutzt wird, muss $h_2\left( k\right)$ teilerfremd zu $m$ sein. Dies lässt sich unter anderem erreichen, wenn $m$ eine Potenz von 2 ist und $h_2\left( k\right)$ immer eine ungerade Zahl berechnet. Eine weitere Möglichkeit ist, für $m$ eine Primzahl und $h_2\left( k\right)$ so zu wählen, dass diese eine Zahl ausgibt, die immer kleiner als $m$ ist. So wären bspw.

\[ h_1\left( k\right) = k \bmod m \] \[ h_2\left( k\right) = 1 + \left(k \bmod m'\right) \] \[ m' = m-1 \]

möglich.

Bei dem Doppelten Hashing sind nun bereits $m^2$ Sondierungssequenzen möglich.

Dynamisches Hashing

Statische Hashverfahren, wie oben beschrieben, sind nicht auf stark wachsende oder schrumpfende Datenmengen ausgelegt. Da ihr Hashbereich fest definiert ist, kommt es schnell zu Überläufen. Bei z. B. steigendem Füllgrad der Tabelle nimmt die Wahrscheinlichkeit von Kollisionen stark zu. Ab dem Zeitpunkt, an dem die Anzahl der indizierten Datensätze größer ist, als die vorhandene Kapazität der Tabelle, werden Kollisionen unausweichlich. Deshalb wird ein dynamisch wachsender Hashbereich benutzt, der genügend Platz für neue Schlüssel hat, aber nicht so groß wird, dass eine schlechte Speicherauslastung entsteht. Das dynamische Ändern der Größe hat jedoch die Folge, dass sich auch der Wertebereich der Hashfunktion verändert. Im schlimmsten Fall müsste bei jeder Änderung auch der bereits bestehende Hashwert von gespeicherten Daten verändert werden. Um dies zu vermeiden gibt es eigens für das dynamische Hashing entwickelte Hashfunktionen:

• Erweiterbares Hashing
• Lineares Hashing
• Virtuelles Hashing

Belegarbeit zu dynamischem Hashing

Distributed Hashing

Beim Ditributed Hashing steht die Effiziens, sowie die Dezentralisierung der Speicherung im Vordergrund. Mit der Verbreitung von P2P - Netzen und der Notwendigkeit von dezentralen, verteilten Systemen setzte sich Distributed Hashing durch. Die Daten werden möglichst gleichmäßig über die vorhandenen Speicherknoten verteilt. Jeder Speicherknoten entspricht dabei einem Eintrag in der Hash-Table. Bei Distributed Hash-Tables (DHT) wird zwischen Direct Storage und Indirect Storage unterschieden. D.h. die Daten werden entweder direkt in der DHT abgelegt oder indirekt über einen Verweis in der DHT adressiert.

• Artikel in der iX

• Belegarbeit von zwei Görlitzer Studenten

Komplexität

Wie aus den vorhergehenden Kapiteln ersichtlich wurde, ist die Effizienz bei Hash-Tables am höchsten. Es besteht eine konstante Komplexität zwischen Insert, Search und Delete unabhängig von der Anzahl der Schlüssel, solange man keine Kollisionen mit einbezieht.

Anwendungen

Für Hashing gibt es zahlreiche Verwendungszwecke. Es kommt bei Prüfsummen zum Einsatz, in der Kryptographie für (Pseudo-)Zufallsgeneratoren, bei Hash-Listen und /-Bäumen, sowie bei den hier besprochenen Hash-Tables. Das Anwendungsgebiet von Hash-Tables liegt beim Datenmanagement. Also z.B. beim bereits erwähnten Distributed Hashing, um große Datenbanken auf ein Netzwerk zu verteilen. Der Verteilung von Ressourcen (Traffic und Speicherbedarf) auf mehrere Server und Implementierung von Caches (z.B Browsercache). Des Weiteren um für Compiler Symboltabellen zu erstellen, die jedem Symbol/Bezeichner im Quelltext den Ort, den Datentyp und ggf. einen Pointer zuordnen.

Code-Beispiele

Assoziative Listen mit JavaScript

var Mitarbeiter = new Array(); Mitarbeiter[0] = new Object(); Mitarbeiter[0]["Name"] = "Müller"; Mitarbeiter[0]["Vorname"] = "Hans"; Mitarbeiter[0]["Wohnort"] = "Dresden"; Mitarbeiter[1] = new Object(); Mitarbeiter[1]["Name"] = "Schulze"; Mitarbeiter[1]["Vorname"] = "Frauke"; Mitarbeiter[1]["Wohnort"] = "Berlin"; for (var i = 0; i < Mitarbeiter.length; i++) { document.write("<dl><dt>Mitarbeiter " + (i + 1) + "<\/dt>"); for (var Eigenschaft in Mitarbeiter[i]) document.write("<dd>" + Eigenschaft + ": " + Mitarbeiter[i][Eigenschaft] + "<\/dd>"); document.write("<\/dl>");

Arrays mit PHP

<?php

// Inititalisierung (optional)
$\$ $list = array();

// Wertzuweisung
$\$ $list[0] = "Eintrag1";
$\$ $list[1] = "Eintrag2";
$\$ $list["zwei"] = "Eintrag3";

// Ausgabe
print_r($\$ $list);

Führt man die Datei aus, erhält man die Ausgabe

Array
(
    [0] => Eintrag1
    [1] => Eintrag2
    [zwei] => Eintrag3
)

Hash-Table in Java

import java.util.Enumeration; import java.util.Hashtable; public class HashTableBeispiel { public static void main(String[] args) { Hashtable<Integer, String> ht = new Hashtable<Integer, String>(); String s; //Einfügen der Schlüssel-Wert-Paare ht.put(2, "Hund"); ht.put(1, "Katze"); ht.put(3, "Regenwurm"); System.out.println("Durchlauf 1:"); for (Integer elem : ht.keySet()) { s = ht.get(elem); System.out.println(elem + " - " + s); } // Wert unter Key "1" wird ersetzt ht.put(1, "Pferd"); System.out.println("\nDurchlauf 2:"); Enumeration<Integer> keys = ht.keys(); while (keys.hasMoreElements()) { Integer i = keys.nextElement(); s = ht.get(i); System.out.println(i + " - " + s); } System.out.println("\nKatze vorhanden? " + ht.containsValue("Katze")); ht.put(4, "Hund"); System.out.println("\nAnzahl Elemente nach einf\u00FCgen von '4': " + ht.size()); System.out.println("\nDurchlauf 3:"); Enumeration<String> vals = ht.elements(); while (vals.hasMoreElements()) { System.out.println(vals.nextElement()); } ht.remove(4); System.out.println("\nAnzahl Elemente nach entfernen von '4': " + ht.size()); ht.clear(); System.out.println("\nAnzahl Elemente nach clear(): " + ht.size()); } }

import java.util.Enumeration; import java.util.Hashtable; public class HashTable { public static void main(String[] args) { Hashtable h = new Hashtable(); //Einfügen der Adressen h.put("Jens", "s3jeklin@stud.hszg.de"); h.put("Daniel", "s3dafran@stud.hszg.de"); //Ausgabe Enumeration e = h.keys(); while (e.hasMoreElements()) { String alias = (String) e.nextElement(); System.out.println( alias + " --> " + h.get(alias) ); } } }

Übungen

Aufgabe 1

Implementiere eine Hash-Table oder Assoziative Liste in einer Programmiersprache deiner Wahl. Orientiere dich dabei an den Code-Beispielen im vorhergehenden Kapitel.

Aufgabe 2

Illustriere das Einfügen der Schlüssel $5, 28, 19, 15, 20, 33, 12, 17, 10$ in eine Hashtabelle der Größe $m = 9$. Die Hash-Funktion sei $h(k) = k \bmod m$. Wo treten Kollisionen auf und wie können diese aufgelöst werden?