Hash Tables und Assoziative Listen SS12
Aus ProgrammingWiki

Inhaltsverzeichnis |
Assoziative Datenfelder
Wörterbuch-Beispiel
Wörterbücher werden verwendet, um Wörter und deren Definitionen, Beispiele etc. abzubilden. Üblicherweise sind die Wörter dabei alphabetisch geordnet. Die Datenmenge ist meist sehr groß, rund 135.000 Wörter sind im aktuellen Duden vorhanden, das Oxford English Dictionary enthält sogar ca. 600.000 Wörter. Um den Wörtern ihre Definitionen zu ordnen zu können, werden beide assoziativ (verknüpft) abgebildet. Eine Verknüpfung von Wort und Definition wird Schlüssel-Wert-Paar bezeichnet, wobei jedes Wort als ein einzigartiger Schlüssel und jede Definition als ein Wert definiert ist.
Auch in einer Anwendung kann es Situationen geben, in denen man mit solchen Datenmengen arbeiten muss. In Anbetracht dessen stellen sich dabei folgende Fragen:
Gibt es eine effiziente Möglichkeit:
- neue Daten der Menge hinzuzufügen?
- vorhandene Daten zu entfernen?
- nach vorhandene Daten zu suchen?
Wir werden diese Fragen in den nachfolgenden Abschnitten beantworten.
Charakterisierung
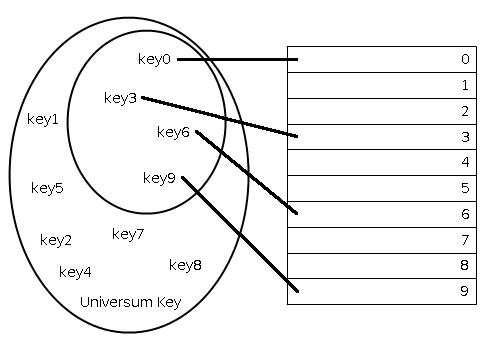
Es gibt diverse Möglichkeiten, um mit Datenmengen wie oben beschrieben umzugehen. Eine davon ist das assoziative Datenfeld. In einem assoziativen Datenfeld $D$ werden Informationen wie im Wörterbuch als Schlüssel-Wert-Paare gespeichert, wobei die Schlüssel nichtnumerisch sind. Sie stammen dabei meist aus einem sehr großen Universum $Key$.
Es werden drei Operationen zur Verfügung gestellt. Wir nehmen an, dass jedes Element $e$ auf einen einzigartigen Schlüssel $key(e) \in Key$ abgebildet wird:
- Hinzufügen eines Elements
- $d.insert(e : Element) : D := D \cup \{e\}$
- Entfernen eines Elements
- $d.remove(k : Key) : D := D \backslash \{e\}$
- Finden eines Elements
- $d.find(k : Key) :$ Wenn ein $e$ in $D$ vorhanden ist, für das $key(e) = k$ ist, dann Rückgabe $e$; sonst Rückgabe $null$
Wie bereits erwähnt, ist die Menge der potenziellen Schlüssel der Menge $Key$ sehr groß.
Man nehme beispielsweise Zeichenketten, die aus 7 Zeichen bestehen, wobei jedes Zeichen ein Buchstabe aus dem Alphabet $a-z$ ist. Bereits bei 7 Zeichen gibt es über $26^{7}$, also mehr als 8 Milliarden mögliche Zeichenketten. Da die Schlüssel die Indizes bestimmen an denen die Paare im Datenfeld gespeichert werden, müsste vorab viel Speicherplatz reserviert werden. Im Vergleich dazu werden aber meist nur sehr wenige Informationen gespeichert und damit wenige Schlüssel verwendet. Man benötigt also eine Möglichkeit die Schlüssel aus $Key$ auf eine kleinere Menge abzubilden und damit den benötigten Speicherplatz zu verringern.
Implementiert werden sie durch Hash Tables.
Anwendungen
Assoziative Datenfelder sind vielseitige Datenstrukturen und finden deshalb in vielen Bereichen Anwendung:
- Compiler (als Symboltabellen)
- Kombinatorische Suchprogramme benutzen sie, um herauszufinden, ob eine gewisse Situation schon einmal betrachtet wurde
- JOIN-Operationen bei Datenbanken
Hash Tables
Idee
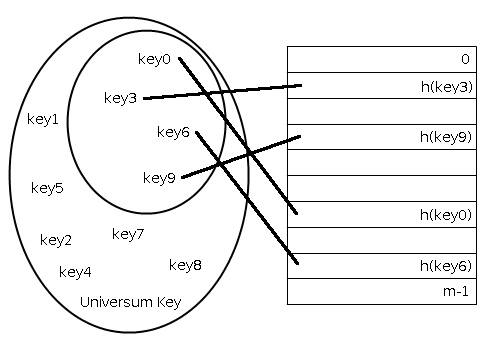
Die Idee hinter einer Hash Table ist die Verwendung von mathematischen Funktionen, um die Datensätze auf unterschiedliche Positionen eines Datenfelds abzubilden und somit die Größe des Datenfeldes gering zu halten.
Die nichtnumerischen Schlüssel werden dabei meist in kleinere Stücke "zerhackt". Daher kommt auch der englische Begriff to hash, was soviel bedeutet wie zerhacken, zerkleinern. Die kleineren Stücke werden als Nummern interpretiert mit denen danach die Berechnungen durchgeführt werden.
Charakterisierung
Eine Hash Table $t$ hat die Größe $m$ und $Key$ ist die Menge potenzieller Schlüssel. Eine sogenannte Hash-Funktion $h$ berechnet aus dem Schlüssel $key \in Key$ des Elements $e$ den Hashwert $h(key(e))$ (kurz auch $h(e)$). Dieser wird dann verwendet um das betreffende Schlüssel-Wert-Paar auf eine Position im Bereich von $0\dots m-1$, die Indizes von $t$, abzubilden: $$h : Key \rightarrow \{0,\dots,m-1\}$$
Der Füllgrad einer Hash Table $\alpha$ beschreibt das Verhältnis der Anzahl gespeicherter Datensätze $n$ zu der Größe $m$ der Hash Table. Für den Füllgrad gilt also $\frac{n}{m}$ (empfohlen werden Werte zwischen 0,75 und 0,8). Idealerweise wird in jedem Tabelleneintrag $t[h(e)]$ höchstens ein Schlüssel-Wert-Paar gespeichert. Ist das der Fall, dann gilt für den Füllgrad $\alpha \leq 1$ und die Ausführungszeiten für die drei Operationen sind konstant, also $\mathcal{O(1)}$.
Hash-Funktionen
Eine gute Hash-Funktion ist wichtig für eine Hash Table. Gut bedeutet dabei, dass die Schlüssel-Wert-Paare so gestreut werden, dass möglichst wenig Kollisionen auftreten. Außerdem muss eine Hash-Funktion deterministisch sein, also bei gleichen Eingaben immer die gleichen Ergebnisse liefern. Eine oft genutzte Funktion ist die Division mit Rest. Die Hash-Funktion lautet $$h(key) = key \bmod m$$ wobei $m$ die Größe der Hash Table ist.
Beispiel: Gegeben seien eine Hash Table der Größe $m = 13$, die Schlüssel 4, 10, 25, 37, 6, 14, 47, 29 und die Hash-Funktion $h(key) = key \bmod m$. Dann ergibt sich folgende Tabelle:
| Index | Schlüssel |
|---|---|
| 0 | |
| 1 | 14 |
| 2 | |
| 3 | 29 |
| 4 | 4 |
| 5 | |
| 6 | 6 |
| 7 | |
| 8 | 47 |
| 9 | |
| 10 | 10 |
| 11 | 37 |
| 12 | 25 |
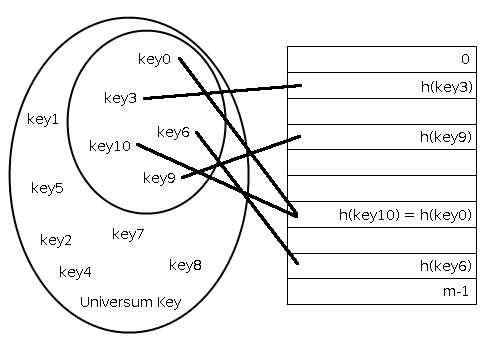
Kollisionen
Spätestens wenn $\alpha > 1 $ kann es auch vorkommen, dass mehr als ein Element auf einen Tabelleneintrag abgebildet wird. Es seien zwei verschiedene Elemente $e1$ und $e2$ gegeben, für die gilt $h(e1) = h(e2)$, dann kommt es zu einer sogenannten Kollision. Um diese Kollisionen auflösen zu können, gibt es unterschiedliche Kollisionsauflösungsstrategien. Im Allgemeinen wird bei diesen Strategien zwischen Hashing mit offener Adressierung und Hashing mit geschlossener Adressierung unterschieden. Zu Hashing mit offener Adressierung zählen unter anderem Hashing mit linearer Sondierung, Hashing mit quadratischer Sondierung, Doppel-Hashing und Brent-Hashing. Zu Hashing mit geschlossener Adressierung zählt das Hashing mit Verkettung.
Kollisionsauflösung
Bei der Kollisionsauflösung gibt es die Möglichkeit der offenen und der geschlossenen Adressierung. Beide Arten unterscheiden sich dahingehend, wie nach einem alternativen Ort in der Hash Table für das Schlüssel-Wert-Paar im Falle einer Kollision gesucht wird. Bei der offnenen Adressierung wird solange ein alternativer Hashwert ausprobiert, bis dieser auf eine freie Stelle in der Hash Table abgebildet werden kann. Im Gegensatz dazu wird das Schlüssel-Wert-Paar bei geschlossener Adressierung einfach an einen bereits vorhandenen Datensatz angehangen.
Verkettung
Bei der Verkettung wird der Datensatz immer an der Position eingefügt, die durch die Hash-Funktion berechnet wurde. Befindet sich bereits ein Datensatz an dieser Position, dann wird der neue Datensatz einfach hinten angehangen und mit dem vorhergehenden "verkettet". Dies kann z.B. mithilfe von Listen oder Bäumen realisiert werden.
Das Einfügen und Löschen eines Datensatzes kann sogar im worst-case in konstanter Zeit $\mathcal{O(1)}$ durchgeführt werden (unter der Voraussetzung, dass Duplikate zugelassen sind, oder, dass der einzufügende Datensatz in der Hash Table noch nicht vorhanden ist). Dazu kann man sich doppelt-verkettete Listen oder einfach-verkettete Listen mit einer Erweiterung zu Nutze machen. Anders sieht es beim Suchen aus. Der worst-case für diese Operation liegt hier bei $\mathcal{O(n)}$, wobei $n$ die Anzahl der sich in der Hash Table befindenden Datensätze ist. Das ist dann der Fall, wenn die Hash-Funktion alle Datensätze auf die gleiche Position abbildet und damit eine Liste der Größe $n$ durchsucht werden muss.
Wieso wird die Verkettung verwendet, obwohl sie für die Suche im worst-case so ein schlechtes Verhalten aufweist?
Betrachten wir den average-case einer Suche in einer Hash Table mit Verkettung. Jeder Tabelleneintrag speichert im Mittel eine Liste der Länge $\frac{n}{m} = \alpha$. Unter der Annahme, dass der Hashwert in $\mathcal{O(1)}$ berechnet wird, heißt das sowohl für die erfolgreiche, als auch für die erfolglose Suche, dass die erwartete Laufzeit bei $\mathcal{O(1 + \alpha)}$ liegt. Nehmen wir weiter an, dass $n$ proportional zu $m$ ist ($n$ = $\mathcal{O(m)}$). Dann beträgt die mittlere Laufzeit für eine erfolgreiche bzw. erfolglose Suche $\mathcal{O(1)}$.
Das bedeutet, dass das Einfügen, Löschen und Suchen im Mittel in $\mathcal{O(1)}$ durchführbar sind.
Java-Definition einer Hash Table mit Verkettung
Einfügen von $n$ Elementen
Suchen nach einem Element in $n$ Elementen
Löschen eines Elements in $n$ Elementen
Lineare Sondierung
Das Prinzip der linearen Sondierung ist wie folgt: Wird beim Einfügen eines Datensatzes festgestellt, dass die errechnete Position bereits belegt ist, dann untersucht man die Position rechts daneben. Dies wird solange durchgeführt, bis eine freie Position gefunden wurde oder einmal alle Positionen probiert wurden. Dieser Algorithmus ist zwar einfach zu implementieren, es besteht allerdings das Risiko der Clusterbildung, also Bereiche, in denen viele Elemente hintereinander stehen.
Es wird eine alternative Hash-Funktion $$h'(key, i) = (h(key) + i) \bmod m$$ angewendet, wobei $i$, mit $0 \le i \le m-1$, die Anzahl der ausprobierten Tabelleneinträge ist.
Das Einfügen und Suchen eines Datensatzes ist einfach zu bewerkstelligen. Doch wie sieht es mit dem Löschen aus? Ein Datensatz kann nicht einfach aus der Hash Table gelöscht werden. Es würden die rechts von ihm befindlichen Datensätze nicht mehr erreichbar sein, da ein Suchvorgang stoppt, wenn er auf einen leeres Feld trifft. Dies trifft natürlich nur auf Datensätze zu, deren Position durch lineare Sondierung berechnet wurde.
Beispiel: Gegeben seien die Schlüssel $key1$, $key2$ und $key3$, für die gilt $h(key1) = h(key3)$ und $h(key2) = h(key1) + 1$. Dann würde $key3$ durch lineare Sondierung an der Stelle $h(key1) + 2$ eingefügt werden. Wird nun $key2$ einfach gelöscht, so entsteht eine Lücke und $key3$ ist nicht mehr erreichbar.
Wie könnte dieses Defizit behoben werden?
Die einfachste Lösung ist das Löschen zu verbieten. Eine weitere Lösung ist, die zu löschenden Elemente zu markieren. Dadurch kann zwar das Problem der Suche gelöst werden, allerdings nimmt die Menge der belegten Einträge zu, wodurch Suchvorgänge verlangsamt werden können.
Java-Definition einer Hash Table mit linearer Sondierung
Einfügen von $n$ Elementen
Suchen nach einem Element in $n$ Elementen
Löschen eines Elements in $n$ Elementen
Quadratische Sondierung
Beim der quadratischen Sondierung wird ähnlich vorgegangen wie bei der linearen Sondierung. Es wird wieder nach einer freien Position in der Hash Table gesucht, allerdings nicht ein Feld rechts davon. Stattdessen entfernt man sich von der ursprünglichen Position in quadratischen Schritten. Die Hash-Funktion lautet dabei $$h'(key, i) = (h(key) + i^{2}) \bmod m$$ wobei $i$, mit $0 \le i \le m-1$, die Anzahl der ausprobierten Tabelleneinträge ist. Dadurch soll die Cluster-Bildung der linearen Sondierung vermieden werden. Es sind nur kleine Anpassungen des Quellcodes der linearen Sondierung notwendig, um daraus eine Hash Table mit quadratischer Sondierung zu erstellen.
Java-Definition einer Hash Table mit quadratischer Sondierung
Einfügen von $n$ Elementen
Suche nach einem Element in $n$ Elementen
Löschen eines Elements in $n$ Elementen
Auch hier besteht wieder das Problem beim Löschen eines Datensatzes, welches schon bei der linearen Sondierung beschrieben wurde. Zur Lösung diese Problems können die gleichen Lösungsmöglichkeiten eingesetzt werden.
Brent-Hashing
Das Brent-Hashing ist eine Erweiterung des Doppel-Hashing. Beim Doppel-Hashing wird im Kollisionsfall eine Sondierung mithilfe einer zweiten Hash-Funktion durchgeführt. Die allgemeine Funktion lautet $$h_{i}(k) = (h(k) + i * h'(k)) \bmod m$$ mit $m$ = Größe der Hash Table und $i$ = Anzahl der ausprobierten Tabelleneinträge. Der Algorithmus wird solange ausgeführt, bis ein freier Tabelleneintrag gefunden wird.
Brent-Hashing baut auf diesem Ansatz auf. Er unterscheidet sich zum Doppel-Hashing dahingehend, dass der Algorithmus entscheidet, ob der im Tabelleneintrag vorhandene Datensatz oder der neue Datensatz verschoben wird. Weitere Informationen findet man hier $\rightarrow$ Brent-Hashing
Universelles Hashing
Wird in einer Anwendung eine feste Hash-Funktion verwendet, dann kann es sein, dass dies ausgenutzt wird um bei Verwendung bestimmter Schlüssel eine Hash Table so zu füllen, dass eine Suche nur noch in linearer Zeit $O(n)$ durchgeführt werden kann (auch möglich bei einer schlechten Hash-Funktion). Um dies zu verhindern, wird universelles Hashing verwendet. Dabei gibt es eine Menge bzw. Klasse $H$ unterschiedlicher Hash-Funktionen aus der - bei gleicher Wahrscheinlichkeit der Hash-Funktionen - zufällig eine Funktion ausgewählt wird. Dadurch ist es möglich, dass ein Schlüssel auf unterschiedliche Positionen in einer Hash Table abgebildet werden kann. Es handelt sich dabei also um eine Strategie zur Kollisionsvermeidung. Die Wahrscheinlichkeit einer Kollision ist dabei nicht größer als $\frac{1}{m}$.
Folgende Gleichung beschreibt den Sachverhalt
$$\forall x \neq y \in Key : |\{h \in H : h(x) = h(y)\}| = \frac{|H|}{m}$$
Perfektes Hashing
Hinter dem perfekten Hashing steht die Idee, eine Suche in einer Hash Table auch im worst-case in $\mathcal{O(1)}$ durchführen zu können. Dazu muss die Menge der Schlüssel statisch (unveränderlich) sein, das heißt es sind weder Einfüge- noch Lösch-Operationen möglich. Außerdem wird zweistufig gearbeitet, jeweils mit universellem Hashing. Das Prinzip ähnelt dem Hashing mit Verkettung, allerdings werden keine Listen oder Bäume erzeugt, sondern sekundäre Hash Tables. Um Kollisionen in den sekundären Hash Tables zu vermeiden, muss deren Länge $m$ gleich dem Quadrat von $n$ in diesen sekundären Hash Tables gespeicherten Datensätze sein. Die Wahrscheinlichkeit einer Kollision bei $m = n^{2}$ ist dann kleiner als $\frac{1}{2}$.
Aufgaben
Aufgabe 1
Informieren Sie sich über weitere Hashing-Algorithmen:
- Kuckucks-Hashing
- Doppel-Hashing
- Brent-Hashing
Aufgabe 2
Gegeben sei eine Hash Table der Größe $m$ = 17, sowie die Schlüssel 45, 88, 68, 31, 101, 21, 74, 18, 59, 111. Die Hash-Funktion lautet $h(key) = key \bmod m$. Erzeugen Sie die Hash Table!
Aufgabe 3
Gegeben sei eine Hash Table der Größe $m$ = 13, sowie die Schlüssel 79, 25, 31, 53, 7, 64, 14. Nutzen Sie bei Kollisionen die quadratische Sondierung. Die Hash-Funktion lautet $h'(key, i) = (h(key) + i^{2}) \bmod m$. Erzeugen Sie die Hash Table!