Aus ProgrammingWiki

Autoren

Hannes Kretschmer

Julian Hilsberg

Inhaltsverzeichnis 1 Eingangsbeispiel 1.1 Königsberger Brückenproblem 2 Grundbegriffe der Graphentheorie 2.1 Graph 2.2 Adjazenz / Inzidenz 2.3 Wege und Zusammenhang 2.4 Graphentypen 3 Datenstrukturen für Graphen 3.1 Auswahl - Operationen für Graphen 3.2 Adjazenzmatrix 3.3 Adjazenzliste 3.4 Kantenliste 3.5 Bewertete Graphen 3.6 Inzidenzmatrix 4 Übungsaufgaben 5 Literatur

Eingangsbeispiel

Graphen sind eine Datenstruktur, die überall in der Informatik auftritt. Algorithmen für das Arbeiten mit ihnen ist von fundamentaler Bedeutung. Es gibt viel Probleme, die unter Verwndung von Graphen definiert sind.

Königsberger Brückenproblem

Das Königsberger Brückenproblem ist eine mathematische Fragestellung des frühen 18. Jahrhunderts. Es wird anhand sieben Brücken der Stadt Königsberg beschrieben. Das Problem bestand darin, zu klären, ob es einen Weg gibt, bei dem man alle sieben Brücken über den Pregel genau einmal überquert. Falls dies möglich ist, stellt sich die Frage, ob ein Rundweg möglich ist, bei dem man wieder zum Ausgangspunkt gelangt. Wie Leonhard Euler 1736 bewies, war ein solcher Weg bzw. „Eulerscher Weg“ in Königsberg nicht möglich, da zu allen vier Ufergebieten bzw. Inseln eine ungerade Zahl von Brücken führte. Es dürfte maximal zwei Ufer mit einer ungeraden Zahl von angeschlossenen Brücken geben. Diese zwei Ufer könnten Ausgangs- bzw. Endpunkt sein. Die restlichen Ufer müssten eine gerade Anzahl von Brücken haben, um sie auch wieder verlassen zu können.

Grundbegriffe der Graphentheorie

Graph

Ein Graph ist eine Kollektion von Knoten und Kanten. Knoten haben Namen und können Träger von Werten, Eigenschaften etc. sein. Kanten stellen Verbindungen zwischen einzelnen Knoten dar.

Mathematisch betrachtet ist ein Graph G eine zweistellige Relation auf einer Menge V. V ist die Menge aller Knoten (engl. vertex). Zwei Knoten $v_1$ und $v_2$ sind in der Relation G, d.h. $(v_1, v_2) \in G$, falls es eine Kante (engl. edge) zwischen $v_1$ und $v_2$ gibt.

Ein Graph $G$ auf $V$ ist somit eine Menge von Paaren der Form $(v, w)$ mit $v \in V$ und $w \in V$ und jede beliebige Teilmenge $G \subseteq V \times V$ ist ein Graph.

Adjazenz / Inzidenz

Ist $[a,b]$ eine Kante des Graphen G, so sind die Knoten $a$ und $b$ adjazent.

Besitzen zwei Kanten denselben Endknoten, sind diese inzident.

Wege und Zusammenhang

Ein Weg (oder Pfad) in einem Graphen ist eine Folge $x = K_1, K_2, \dots, K_n = y$ von Knoten, in der es jeweils Kanten von $K_1$ nach $K_2$, von $K_2$ nach $K_3$ usw. bis nach $K_n$ gibt. Man spricht von einem Weg von x nach y. Auf einem einfachen Weg kommt kein Knoten doppelt vor. Ein einfacher Weg von x nach x heißt Zyklus.Ein ungerichteter Graph heißt zusammenhängend, wenn es je zwischen zwei verschiedenen Knoten einen Weg gibt. ist G nicht zusammenhängend, so zerfällt er in eine Vereinigung zusammenhängender Knoten. Ein zusammenhängender, zyklenfreier, ungerichteter Graph ist ein Baum. Ist G ein Graph auf V und $R \subseteq G$, so ist auch R ein Graph auf V. R heißt Teilgraph von G auf V. Ist G auf V ein zusammenhängender Graph und R ein zyklenfreier zusammenhängender Teilgraph von G auf V, dann ist R ein Spannbaum.

Graphentypen

Übersicht Graphentypen

Ungerichteter Graph ohne Mehrfachkanten

Gerichteter Graph ohne Mehrfachkanten

Ungerichteter Graph mit Mehrfachkanten

Gerichteter Graph mit Mehrfachkanten

Datenstrukturen für Graphen

Auswahl - Operationen für Graphen

Die Wahl der Darstellung eines Graphen muss immer im Bezug auf die mit den Daten durchzuführenden Operationen erfolgen. Die Operationen sind problemabhängig. Die wichtigsten Operationen für Graphen sind:

1. Feststellen, ob ein Paar von Ecken benachbart ist.
2. Bestimmung der Nachbarn einer Ecke.
3. Bestimmung der Nachfolger und Vorgänger einer Ecke in einem gerichteten Graphen.

Neben der Effizienz der Operationen spielt auch der Speicherplatzverbrauch eine große Rolle bei der Wahl einer Datenstruktur. Hierbei stellt man häufig Wechselwirkungen zwischen Speicherplatzverbrauch und Effizienz fest. Eine sehr effiziente Erledigung der Operation benötigt oft mehr Speicherplatz, als eine weniger effiziente. Weiterhin muss Beachtung finden, ob es sich um eine statische oder eine dynamische Anwendung handelt. Bei dynamischen Anwendungen wird der Graph verändert, hierbei benötigt man Operationen zum Löschen und Einfügen von Ecken und Kanten. Oft sollen nur Graphen mit einer speziellen Eigenschaft (z.B. ohne geschlossene Wege) dargestellt werden. In diesen Fällen kann man durch die Wahl einer spezialisierten Datenstruktur die Effizienz weiter steigern.

Adjazenzmatrix

Um einen Graph $G$ darzustellen bietet sich eine $n \cdot n$ Matrix $A(G)$ an. Hierbei ist der Eintrag $a_{ij}$ von $A(G)$ gleich 1, wenn es eine Kante von $i$ nach $j$ gibt, andernfalls gleich 0. Zwei benachberte Knoten werden auch als adjazent bezeichnet. Da diese Matrix direkt die Nachbarschaft der Ecken widerspiegelt, nennt man sie Adjazenzmatrix. Da die Einträge der Matrix nur die Werte 0 und 1 annehmen können, kann $A(G)$ als Boolsche Matrix dargestellt werden. Es lassen sich sowohl gerichtete und ungerichtete Graphen darstellen, wobei im letzten Fall die Adjazenzmatrizen symmetrisch sind.
Ist ein Diagonaleintrag der Matrix gleich 1, so bedeutet dies, dass eine Schlinge vorhanden ist. Um festzustellen ob es einen Weg von $i$ nach $j$ gibt, muss man nur den Eintrag $a_{ij}$ betrachten. Diese Operation kann somit unabhängig von der Größe der Matrix in einem Schritt durchgeführt werden. Um die Nachbarn einer Ecke $i$ in einem ungerichteten Graphen festzustellen, müssen alle Einträge der $i$-ten Spalte oder der $i$-ten Zeile durchsucht werden. Diese Operation ist somit unabhängig von der Anzahl der Nachbarn des Knotens. Für das Auffinden von Vorgängern und Nachfolgern gilt eine analoge Aussage. Im ersten Fall wird die passende Spalte und im zweiten die passende Zeile durchsucht.

Unabhängig von der Anzahl der Kanten, werden immer $n^2$ Speicherplätze benötigt. Da bei einem ungerichteten Graphen, die Adjazenzmatrix symmetrisch ist, reicht es in diesem Fall die Einträge oberhalb der Diagonale zu speichern. Dann benötigt man noch $\frac{n \cdot(n-1)}{2}$ Speicherplätze.

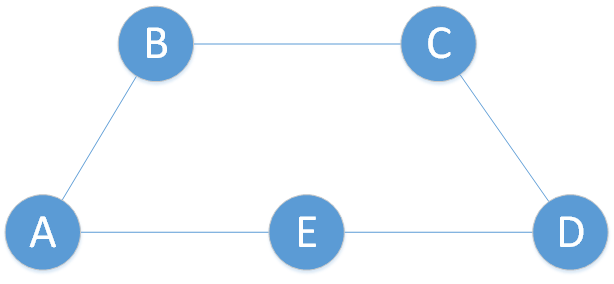
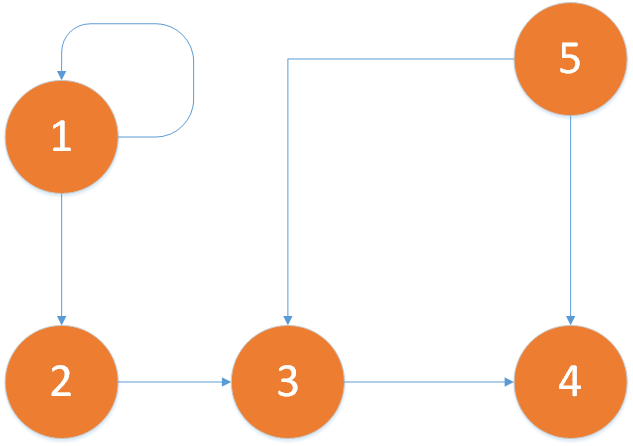
Beispiel:
Adjazenzmatrix des rechts dargestellten Graphen: $A= \begin{pmatrix} 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \end{pmatrix}$

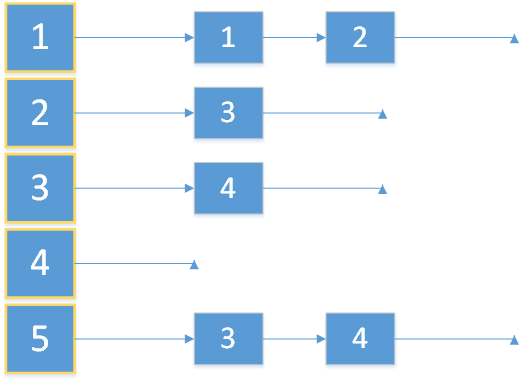
Adjazenzliste

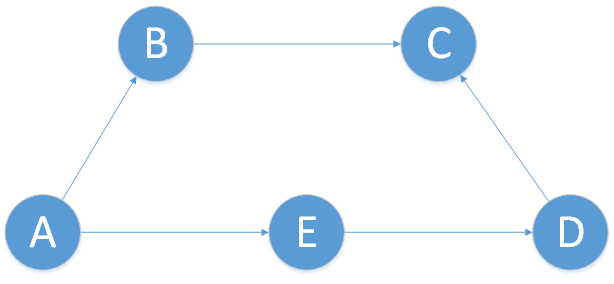
Der Graph wird bei einer Adjazenzliste dadurch dargestellt, dass für jede Ecke die Liste der Nachbarn abgespeichert wird. Es lassen sich gerichtete und ungerichtete Graphen darstellen. Für die Realisierung der Adjazenzliste bieten sich zwei Möglichkeiten an.
Bei der ersten Möglichkeit werden die Listen mit Zeigern realisiert. Der Graph wird durch ein Feld $A$ der Länge $n$ dargestellt. Der $i$-te Eintrag enthält einen Zeiger auf die Liste der Nachbarn von $i$. Die Nachbarn werden als verkettete Liste dargestellt.
Bei der zweiten Möglichkeit verwendet man ein Feld $A$, um die Nachbarn abzuspeichern. Die Nachbarn werden lückenlos nebeneinander abgelegt, zuerst die der Ecke 1, dann die der Ecke 2 usw. Für gerichtete Graphen hat das Feld die Länge $m$ und für ungerichtete Graphen die Länge $2m$. Man benötigt nun eine zweites Feld $N$ der Länge $n$, um festzustellen wo die Nachbarliste für eine bestimmte Ecke beginnt. Dieses Feld enthält nun die Indizes der Anfänge der Nachbarliste.

Um festzustellen ob es eine Kante von $i$ nach $j$ gibt, muss die Nachbarschaftsliste von der Ecke $i$ durchsucht werden. Falls es keine solche Kante gibt, muss die gesamte Liste durchsucht werden. Diese kann bis zu $n-1$ Einträge besitzen. Somit ist diese Operation abhängig von der Größe des Graphen. Sehr einfach ist die Bestimmung der Nachbarn einer Ecke, denn die Liste liegt direkt vor. Aufwendiger ist die Bestimmung der Vorgänger einer Ecke in einem gerichteten Graphen, hierzu müssen alle Nachbarlisten durchsucht werden. Den Vorgang kann man durch die Erstellung von zwei weiteren Feldern, in denen man die Vorgängerlisten gespeichert werden, beschleunigt werden. Danach ist ein direkter Zugriff auf die Vorgänger möglich.
Der Speicheraufwand ist abhängig von der Anzahl der Kanten. Die Adjazenzliste benötigt für einen gerichteten Graphen $n+m$ und für einen ungerichteten Graphen $n+2m$ Speicherplätze. Damit benötigt die Adjazenzliste für einen Graphen, dessen Kantenzahl $m$ viel kleiner ist als die maximale Anzahl, weniger Platz als die Adjazenzmatrix. Bei dynamischen Anwendungen ist die Adjazenzliste basierend auf Zeigern den anderen Darstellungsformen vorzuziehen.

Beispiel:

Kantenliste

Bei der Kantenliste werden alle Kanten explizit in einer Liste gespeichert. Eine Kante wird als ein Paar von Ecken repräsentiert. Wie schon bei der Adjazenzliste bietet sich hier eine Realisierung mittels Zeigern oder Feldern an. Bei der zweiten Möglichkeit wird die Kantenliste mittels eines $2 \cdot m$ Feldes $K$ realisiert. Hierbei ist $(K[1,i], K[2,i])$ die $i$-te Kante. Es werden $2m$ Speicherplätze benötigt.
Bei einem ungerichteten Graphen, muss man die gesamte Liste durchsuchen um festzustellen, ob es eine Kante von $i$ nach $j$ gibt. Bei gerichteten Graphen ist es von Vorteil die Kanten lexikografisch zu ordnen. In diesem Fall kann mit Hilfe der binären Suche schneller festgestellt werden, ob eine Kante von $i$ nach $j$ existiert.
Für ungerichtete Graphen kann die Kantenliste erweitert werden, so dass jede Kante zweimal vertreten ist, einmal in jeder Richtung. Mit diesem erhöhten Speicheraufwand lässt sich dann auch hier die Nachbarschaft zweier Ecken mittels binärer Suche bestimmen.
Für dynamische Anwendungen ist auch hier die Realisierung mittels Zeigern vorzuziehen.
Beispiel:

1

2

3

4

5

6

1	1	2	3	5	5
1	2	3	4	3	4

Bewertete Graphen

In vielen praktischen Anwendungen sind die Ecken oder Kanten eines Graphen mit Werten versehen. Solche Graphen werden ecken- bzw. kantenbewertet genannt. Die Werte stehen in einer festen Wertmenge $W$. Eine Möglichkeit ist die Werte in einem zusätzlichen Feld abzuspeichern und so die schon genannten Darstellungen zu modifizieren.

Bewertete Adjazenzmatrix
Für kantenbewertete Graphen kann die Adjazenzmatrix direkt erweitert werden. Bei der bewerteten Adjazenzmatrix $B$ ist $B[i,j]$ die Bewertung der Kante von $i$ nach $j$. Gibt es keine Kante von $i$ nach $j$, so wird an der Stelle $B[i,j]$ ein Wert, der nicht in $W$ liegt, eingetragen. Dies kann zum Beispiel die Zahl $0$ sein, sofern $0 \notin W$.

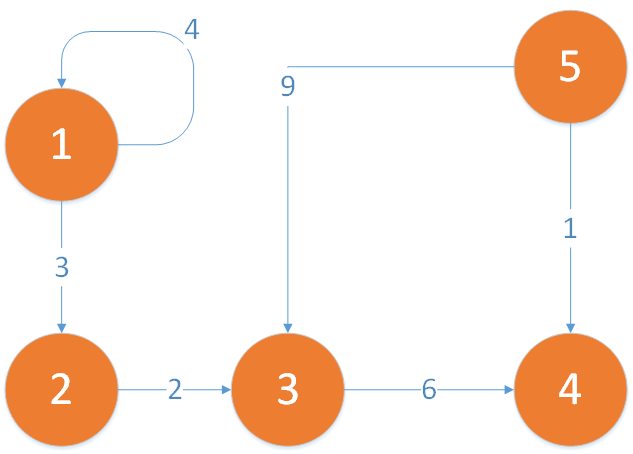
Beispiel:
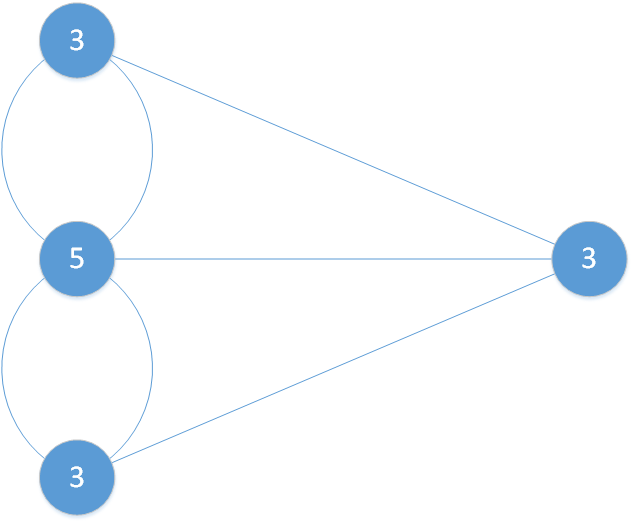
bewertete Adjazenzmatrix des oben dargestellten Graphen: $B= \begin{pmatrix} 4 & 3 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 6 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 9 & 1 & 0 \end{pmatrix}$

Inzidenzmatrix

Eine Inzidenzmatrix speichert die Beziehungen zwischen Ecken und Kanten. Hat der Graph $n$ Ecken und $m$ Kanten entsteht eine $n \cdot m$ Matrix $A$. Der Eintrag $A[i,j]$ gibt dann an ob die $i$-te Kante die $j$-te Ecke enthält. Steht an der Stelle eine 1 ist eine Inzidenzbeziehung vorhanden, steht eine 0 liegt keine Inzidenz vor. Die Matrix braucht $n \cdot m$ Speicherplätze und ist somit für Graphen mit wenigen Kanten besser geeignet als die Adjazenzmatrix.

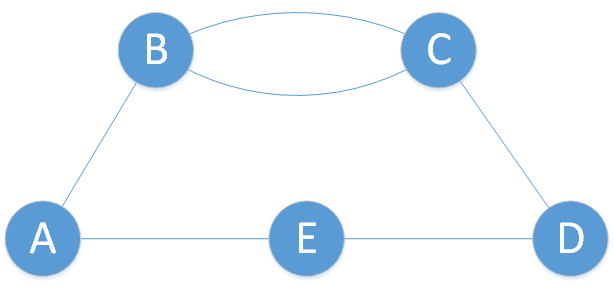
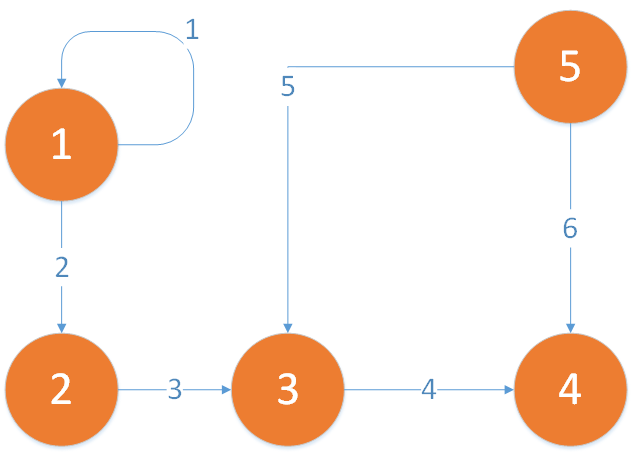
Beispiel:

Inzidenzmatrix des dargestellten Graphen: $A= \begin{pmatrix} e_1& e_2& e_3& e_4 &e_5 &e_6 \\ -0 & 1 & 0 & 0 & 0 & 0 & v_1\\ 0 & -1 & 1 & 0 & 0 & 0 & v_2\\ 0 & 0 & -1 & 1 & -1 & 0 & v_3\\ 0 & 0 & 0 & -1 & 0 & -1 & v_4\\ 0 & 0 & 0 & 0 & 1 & 1 & v_5 \end{pmatrix}$

In diesem Fall wurde die Schlinge mit -0 eingetragen, andere Möglichkeiten wären 2 oder 0. Ideal für Inzidenzmatrizen sind schlingenfreie Graphen.

Übungsaufgaben

Bitte bearbeiten Sie diese Aufgaben sorgfältig. Bei Fragen zur Aufgabenstellung oder für Lösungshinweise stehen wir Ihnen gerne zur Verfügung.

ÜbungGraphenrepräsentation.pdf (0.2 MB)

Literatur

Thomas H. Cormen, Charles E. Leiserson, Ronald Rivest, Clifford Stein

Algorithmen - Eine Einführung, Oldenbourg Verlag, 2. Auflage, 2007. - ISBN 978-3-486-58262-8

Volker Turau

Algorithmische Graphentheorie, Addison-Wesley, 1996. - ISBN 3-89319-938-1

Manfred Nitzsche

Graphen für Einsteiger, Vieweg + Teubner Verlag, 3.Auflage, 2009. - ISBN 978-3-8348-0813-4

H. Gumm, M. Sommer

Einführung in die Informatik, Oldenburg Verlag, 7. Auflage, 2006. - ISBN 978-3-486-58115-7