Graphrepräsentationen SS12
Aus ProgrammingWiki

Inhaltsverzeichnis
|
Rückblick und Motivation
In den letzten Vorlesungen haben wir uns mit sortierten Folgen und Bäumen beschäftigt. Bäume sind spezielle Graphen und waren somit ein erster Einblick in das Gebiet der Graphentheorie, mit der wir uns heute beschäftigen wollen. Wir möchten in dieser Vorlesung die Grundlagen für das sehr komplexe Thema der Graphen legen und euch auf die Stärken dieser Repräsentation von Daten aufmerksam machen.
Graphentheorie
Als ein Teilgebiet der Mathematik untersucht die Graphentheorie Beziehungen und Eigenschaften von Graphen. Die Graphentheorie spielt sowohl in der Mathematik als auch in der Informatik eine wichtige Rolle. Oft können algorithmische Probleme durch Graphenrepräsentation gelöst und umgekehrt Graphenproblematiken mit Hilfe von Algorithmen überwunden werden. Deshalb bilden Graphen einen essentiellen Teil der Komplexitätstheorie in der Informatik.
Königsberger Brückenproblem
Beim Königsberger Brückenproblem handelt es sich um eine mathematische Fragestellung aus dem 18. Jahrhundert. Königsberg wurde am Fluss Pregel erbaut, welcher sich im Stadtgebiet teilt. Über die beiden Flussarme wurden mehrere Brücken gebaut, um schnell von einem Stadtteil zum anderen zu gelangen. Im Jahr 1736 gab es sieben Brücken. Die Einwohner Königsbergs stellten sich die Frage, ob es möglich ist, alle sieben Brücken nur genau einmal zu überqueren. Wenn dies möglich ist, kann man auch einen Rundweg gestalten, bei dem man am Ende wieder am Ausgangspunkt ankommt?
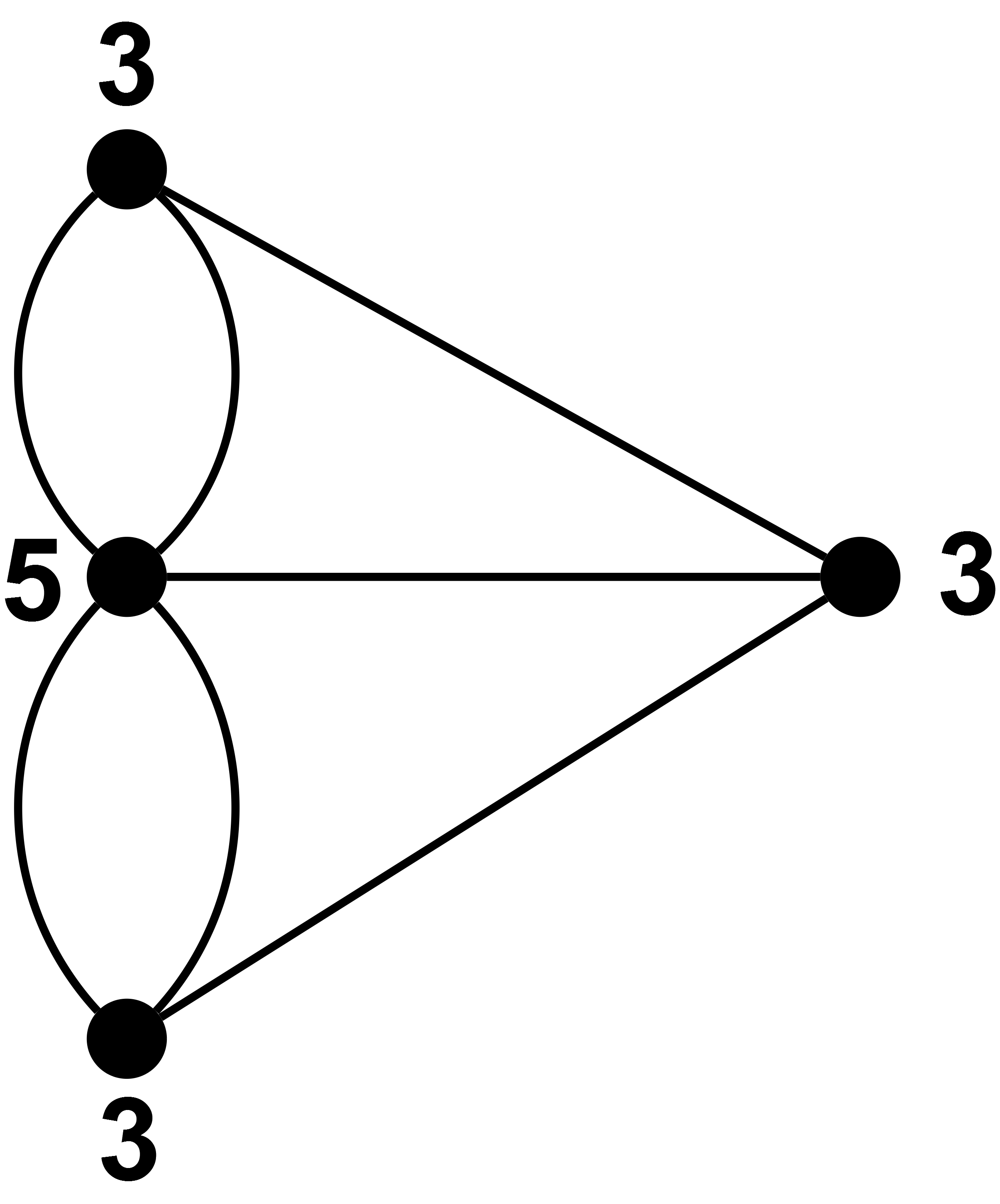
Diesen Fragen nahm sich Leonhard Euler, ein bis heute bedeutender Mathematiker an. 1736 veröffentlichte er seine Arbeit "Solutio problematis ad geometriam situs pertinentis", in der er sich mit dem Königsberger Brückenproblem befasste. Er versuchte sich bei der Untersuchung des Problems nur auf die relevanten Informationen zu beschränken. So stellte er fest, dass es vier Stadtteile gab, die durch sieben Brücken verbunden sind. Er lässt jeden Stadtteil von einen Punkt repräsentiert und jede Brücke stellt eine Linie, also eine Verbindung zwischen zwei Stadtteilen dar. Nach dem Zusammenfügen aller dieser Informationen erhält man die Grafik auf der rechten Seite.
Durch dieses grafische Hilfsmittel ist leicht zu erkennen, dass das Königsberger Brückenproblem nicht lösbar ist. Beim Passieren eines Punktes (Stadtteil) müssen zwei Linien (Brücken) durchlaufen werden (hinein und hinaus). Egal wie in welcher Reihenfolge man versucht die Brücken zu überqueren, ist es unmöglich jede Brücke nur einmal zu benutzen. Somit ist auch ein Rundgang, bei dem Anfangs- und Endpunkt übereinstimmen unmöglich. Um beide Fragen positiv beantworten zu können, müsste von jedem Punkt eine gerade Anzahl von Linien ausgehen, d.h. ein Stadtteil muss mit einer geraden Anzahl von Brücken erreichbar sein. Die Zahlen geben die Anzahl an Linien (Brücken) an, die zum / vom Punkt (Stadtteil) führen.
Leonhard Eulers Arbeit zum Königsberger Brückenproblem gilt als eine der ersten Arbeiten auf dem Gebiet der Graphentheorie.
Applet: Königsberger Brückenproblem (Autoren: Reeken,Scholz,Großer,Frommer,Krivsky)
Grundlegende Begriffe
Um einen leichten Einstieg in die Theorie der Graphen zu ermöglichen, ist es von Nöten, grundlegende Begriffe dieses Themas zu erläutern.
Graphrepräsentation
Im Themenkomplex Graphrepräsentationen sollen Methoden zur Darstellung von Graphen behandelt werden. Dabei wird besonders auf die Struktur von Graphen Wert gelegt, da diese für das sich anschließende Thema, dem Durchsuchen von Graphen, bedeutsam ist.
Graph
Ein Graph $G$ stellt ein Paar $G = (V,E)$ bestehend aus einer endlichen Menge $V$ und einer Menge $E$ von zweielementigen Teilmengen $V$ dar.
Teilgraph
Teilgraph bezeichnet den Teil eines Graphen, für den gilt: mit
und
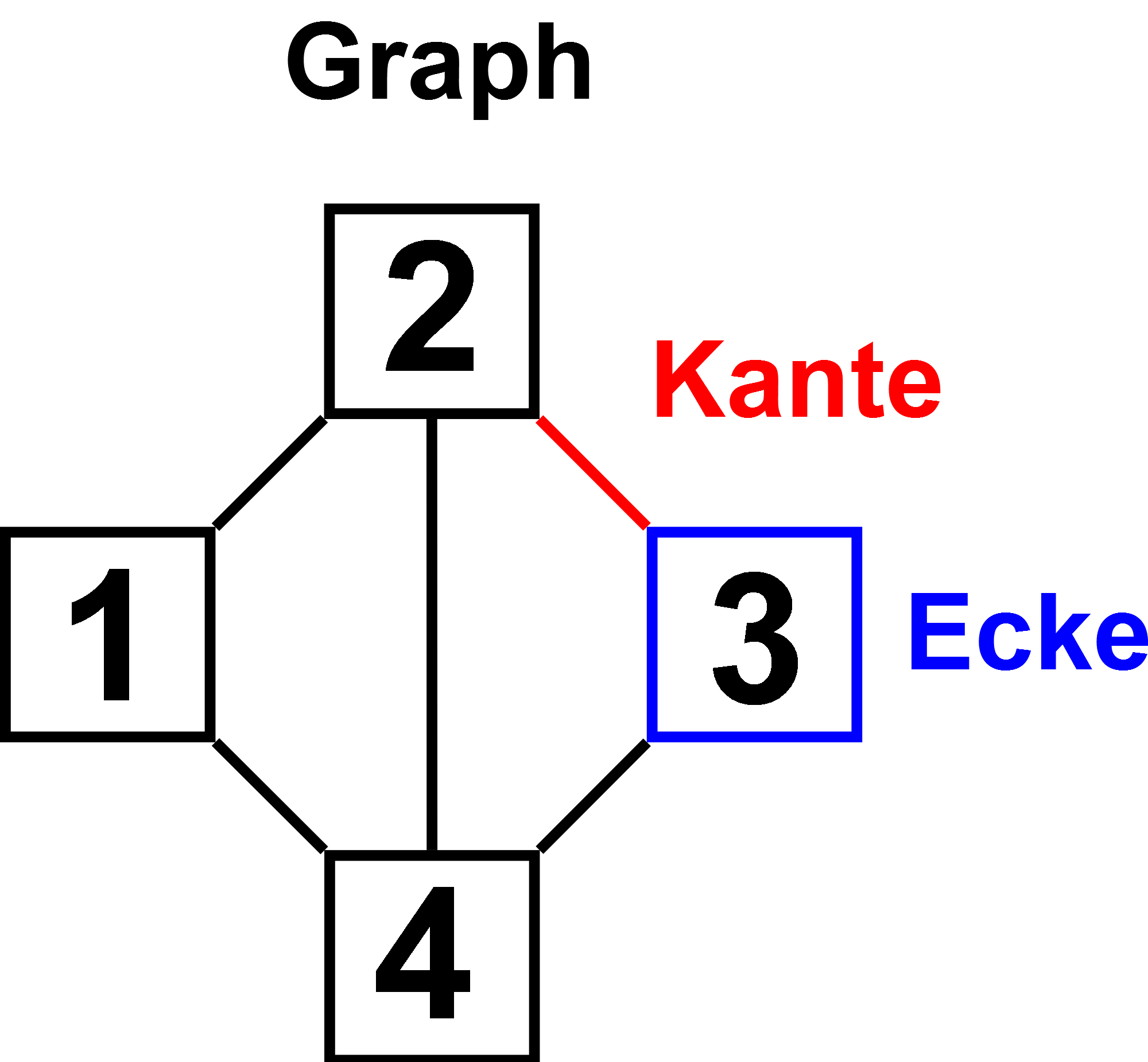
Ecke
Die endliche Menge $V$ repräsentiert die Eckenmenge $V$, bestehend aus Ecken / Knoten (engl. vertex). Ecken sind einfache Objekte mit einem Namen oder einer Eigenschaft. Beispiel: $V = {a,b,c,d}$ Dargestellt ist die Eckenmenge V mit den Ecken des Graphen.
Endecke
Endecken sind die Ecken, die durch eine Kante verbunden sind. So besitzt die Kante $[a,b]$ die Endecken $a$ und $b$.
Kante
Bei der Menge $E$ handelt es sich um die Kantenmenge mit den Teilelementen Kanten (engl. edge), die Verbindungen zwischen je zwei Ecken darstellen. Sie treten stets paarweise auf, da sie die beiden Ecken, die sie verbinden enthalten. Kanten müssen nicht zwingend Verbindungen zweier Ecken sein, sie können genauso eine Ecke mit sich selbst verbinden. Beispiel: $E = \{[a,b],[c,d],[a,c],[b,d]\}$
Aufgabe
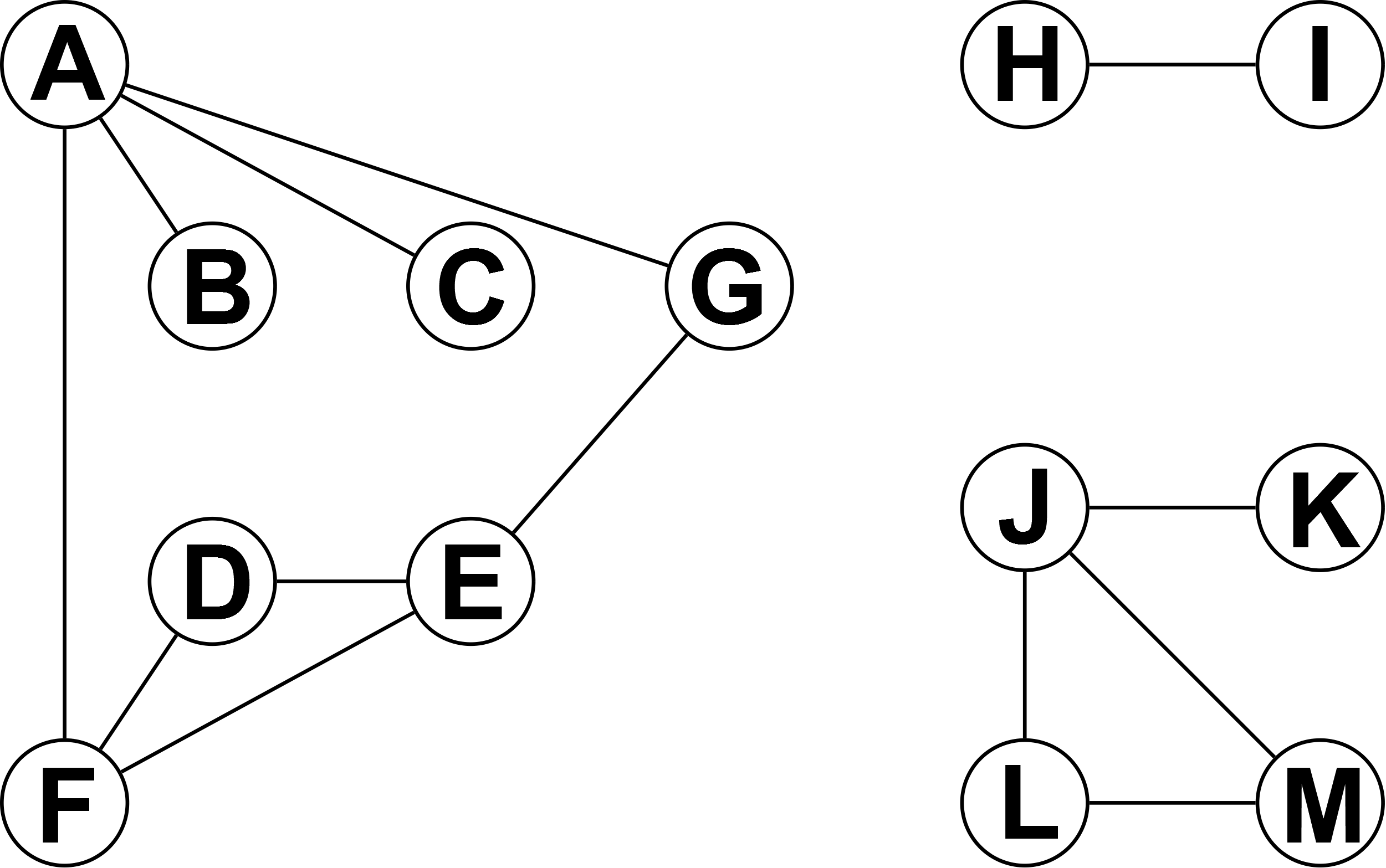
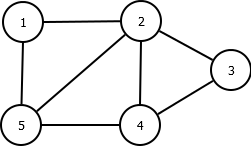
Stellen Sie die Kanten- und Eckenmenge für den Graphen auf der rechten Seite auf (Bild: Teile eines Graphen).
Schlinge
Eine Schlinge ist eine Kante der Form $[a,a]$, wobei die Ecke durch die Kante mit sich selbst verbunden ist. Solche Kantenformen treten häufig bei der Repräsentation von Automaten (DEA, NEA) durch Graphen auf.
Grad
Der Grad $(a)$ einer Ecke wird durch die Anzahl der zu dieser Ecke $a$ inzidenten Kanten beschrieben. Eine Ecke, die den Grad 0 besitzt heißt isoliert.
Adjazenz / Inzidenz
Adjazent heißen zwei Ecken, wenn sie Nachbarn sind. Die Ecken $a, b$ sind demnach adjazent, wenn §[a,b]§ ein Kante des Graphen $G$ ist.
Zueinander Inzident nennt man zwei Kanten, die eine gemeinsame Endecke haben. Eine Ecke ist zu einer Kante inzident, wenn die Ecke Endecke der Kante ist.
Um sich in Graphen fortzubewegen sind weitere Begriffe nötig.
Kantenzug
Eine Folge von Ecken stellt einen Kantenzug der Länge $n-1$ in einem Graph dar, wenn gilt: , so dass die Kante
, für
Der Kantenzug gilt als geschlossen, wenn . Sollte der geschlossene Kantenzug alle Kanten einmal enthalten, so spricht man vom Euler-Zug.
Weg / Pfad und Kreis
Ein Weg / Pfad ist ein Kantenzug, wenn gilt: , für
Ein Pfad kann durch eine Liste repräsentiert werden, bei dem alle Ecken von Ecke $a$ nach Ecke $b$ aufgelistete sind. Die Ecken $a,b$ müssen durch Kanten über beliebig viele Ecken verbunden sein.
Ist der Weg geschlossen, spricht man von einem Kreis / Zyklus.
Graphentypen
Ungerichteter Graph
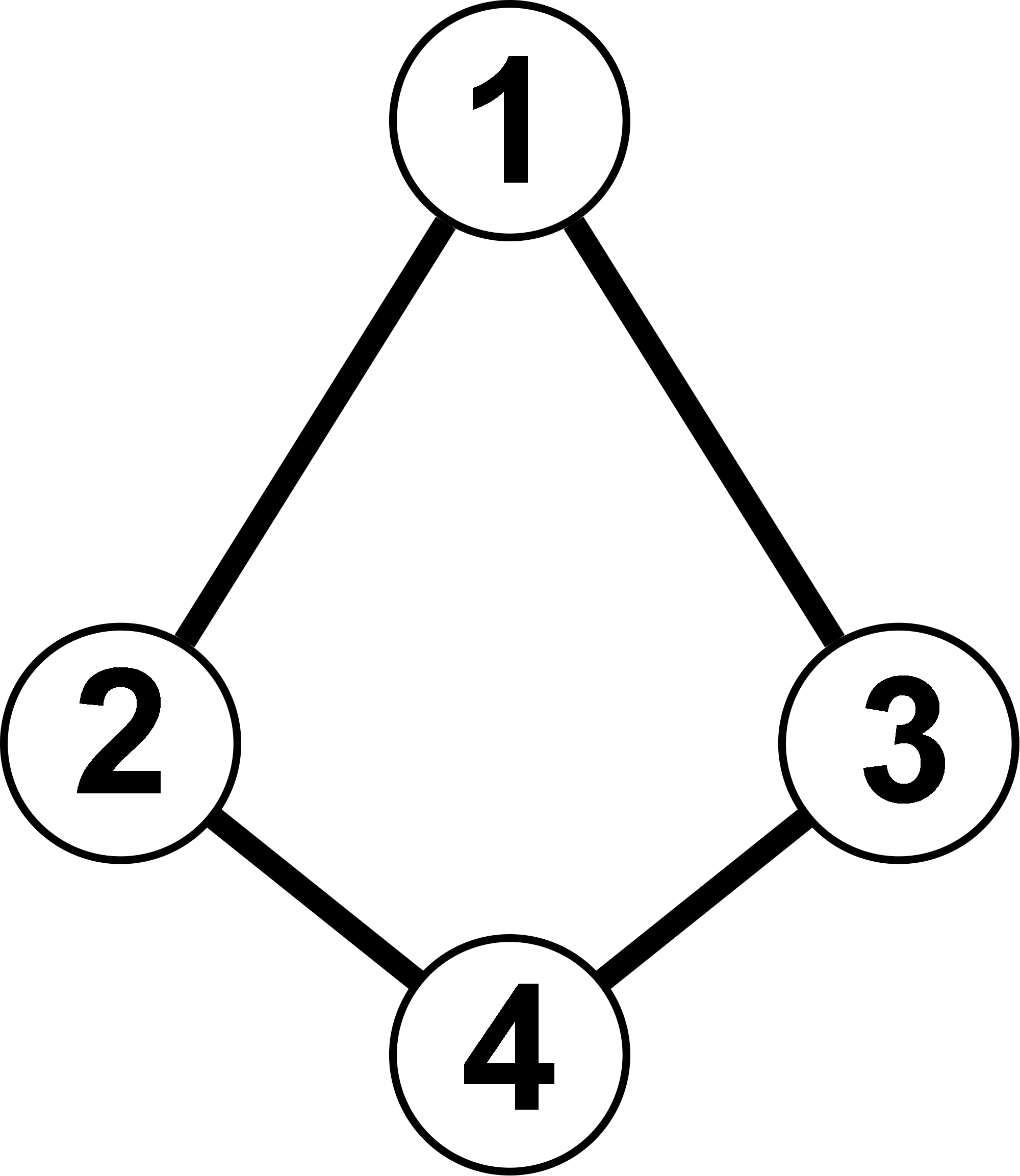
Ein ungerichteter Graph ist ein einfacher Graph ohne Mehrfachkanten, dessen Kanten durch Linien repräsentiert werden. Man kann eine Kante sowohl von der Ecke a nach Ecke b überqueren, als auch umgekehrt. Ein solcher Graph stellt den einfachsten Graphentyp dar.
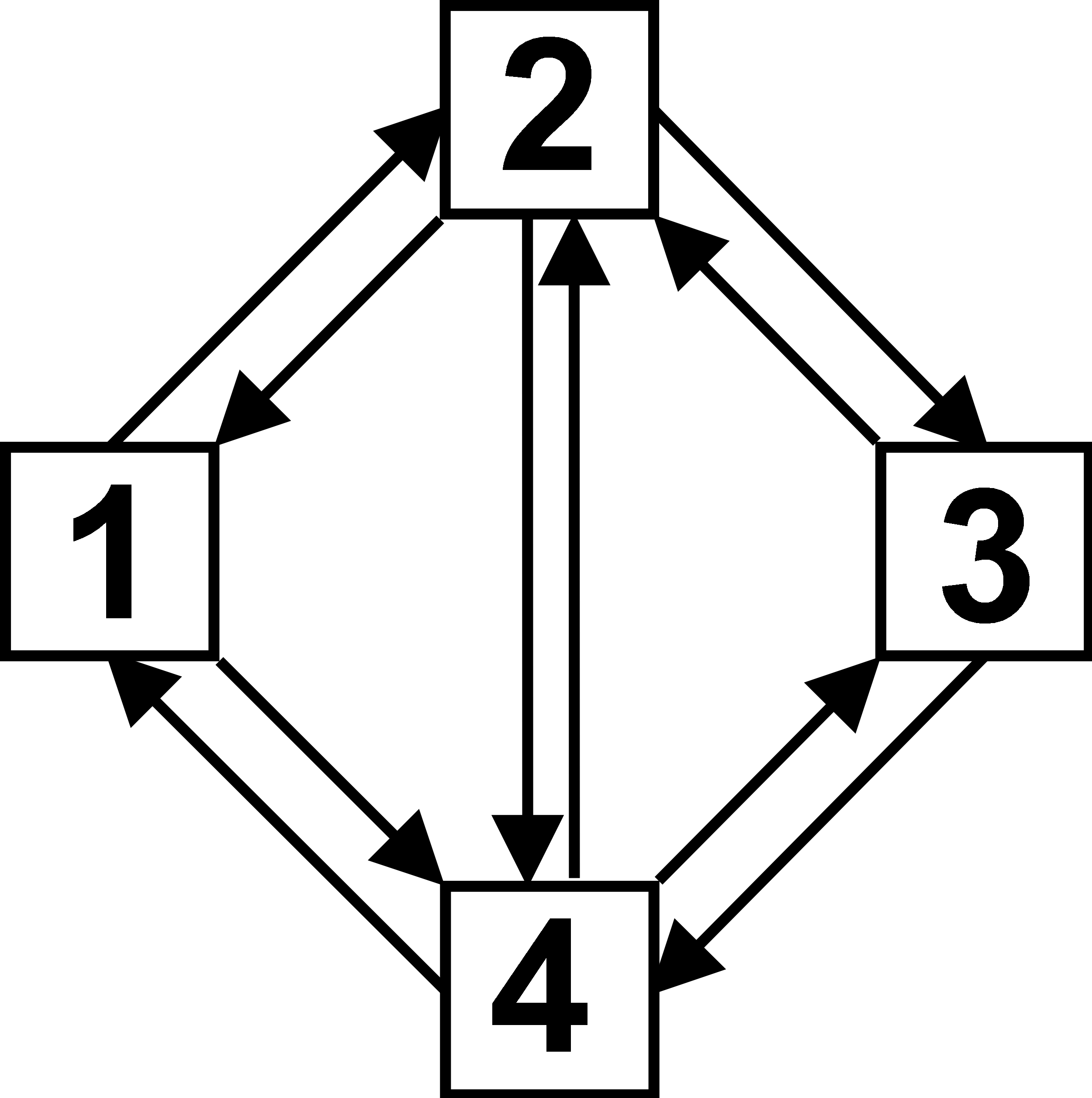
Gerichteter Graph
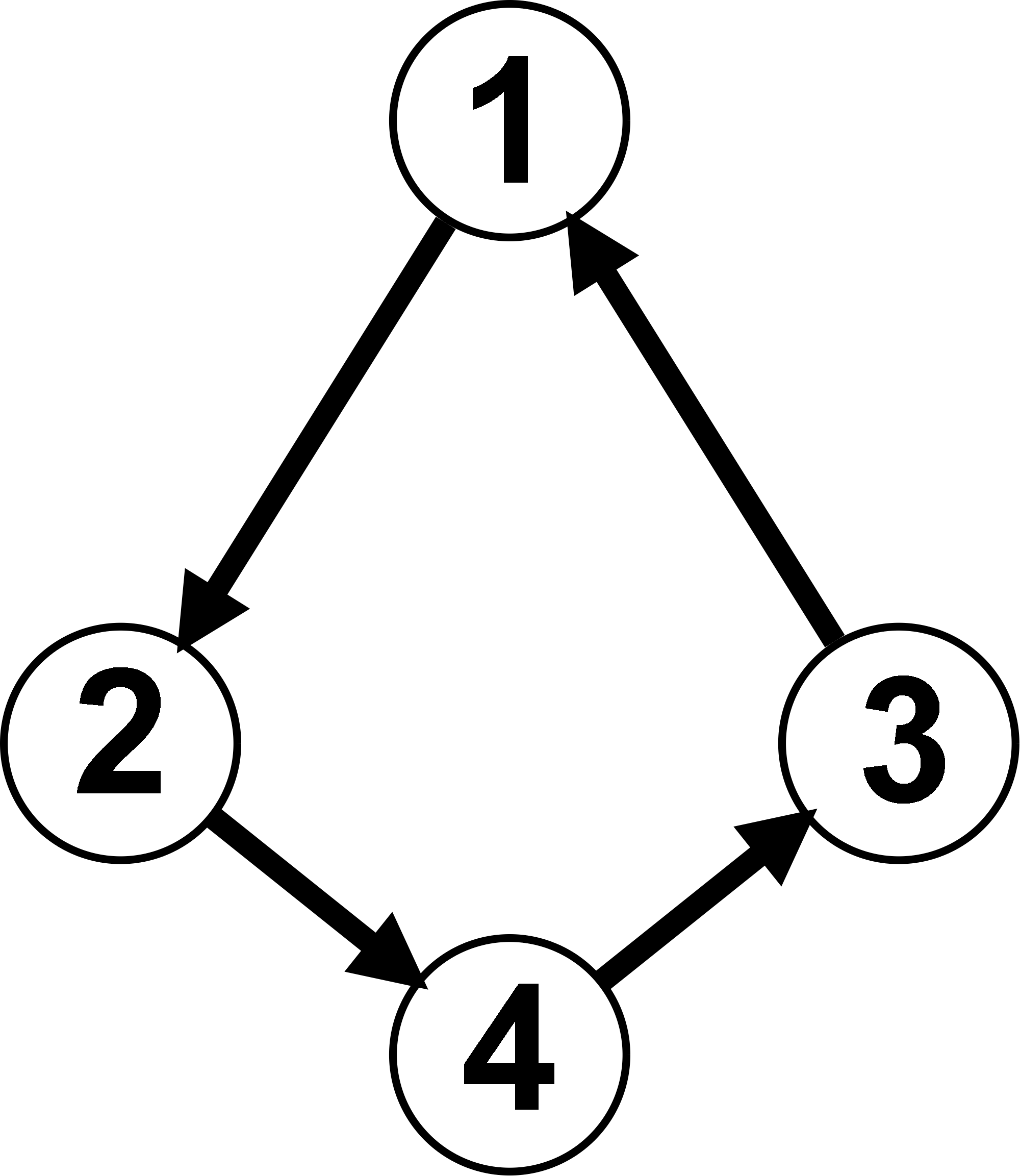
Im Gegensatz zum ungerichteten Graph ist es bei gerichteten Graphen nicht möglich Kanten nach Belieben zu nutzen. Es wird stattdessen stets eine Richtung unter Verwendung einens Pfeils vorgegeben. Der Pfeil zeigt von Ecke a nach Ecke b und gibt somit eine Art Einbahnstraße vor.
Multigraph
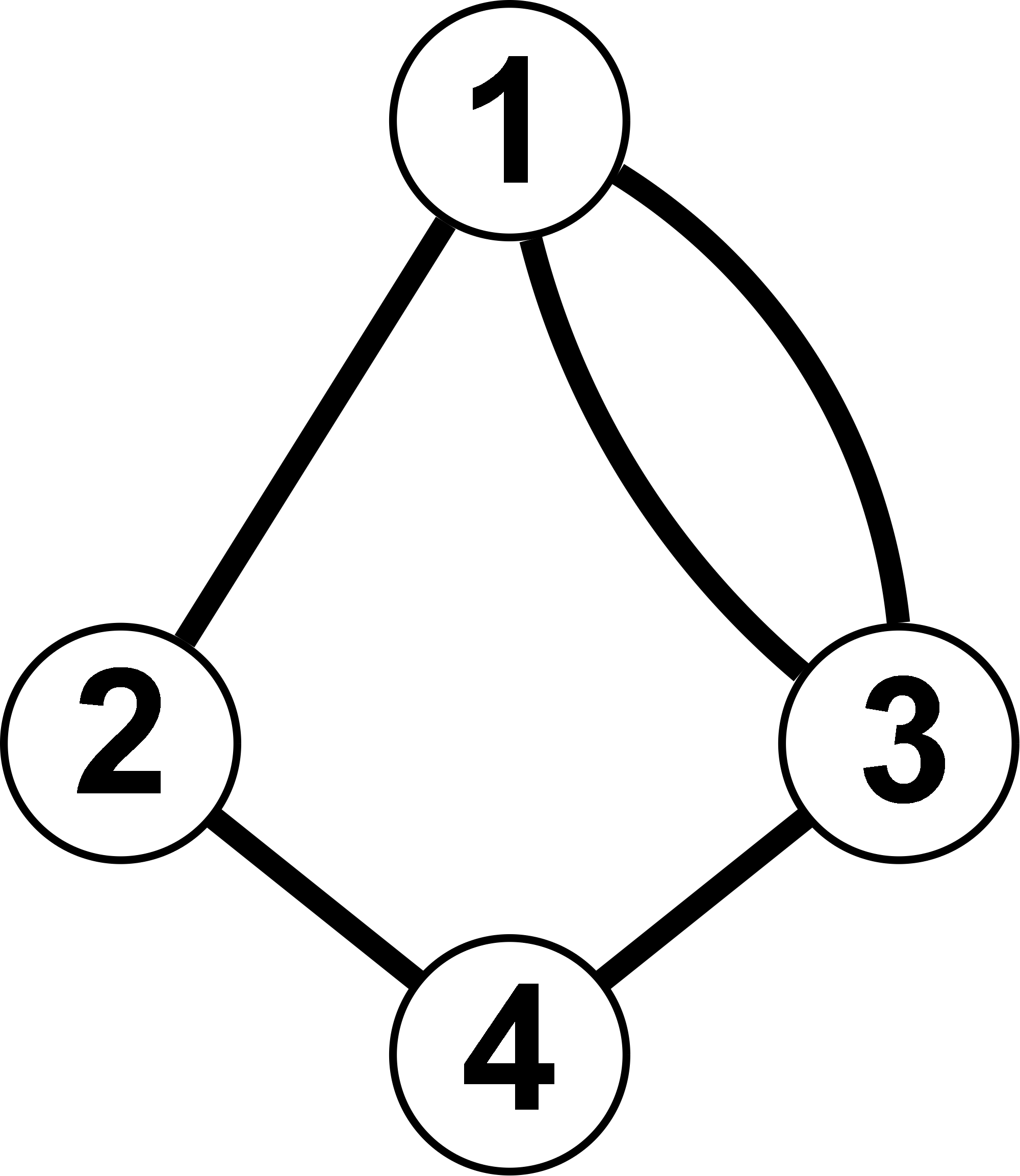
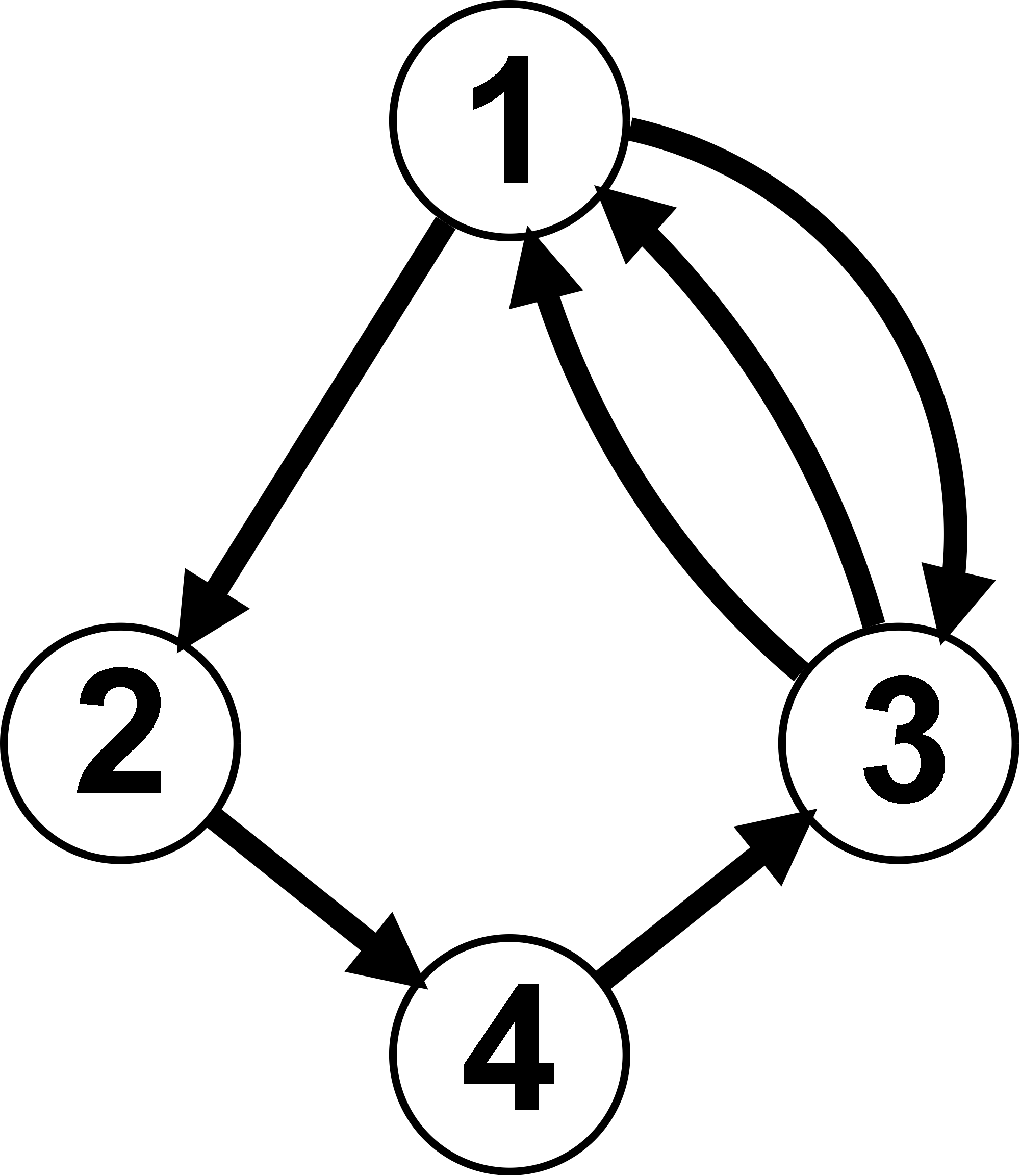
Als Mutltigraph werden komplexere Graphen bezeichnet, die in jede Richtung nicht nur eine Kante zwischen Ecken zulassen, sondern mehrere. Solche Kanten bezeichnet man als Mehrfachkanten. Ein Beispiel für einen Multigraph ist die Visualisierung des Königsberger Brückenproblems.
Unvollständiger Graph
Unvollständige Graphen enthalten nicht alle maximal möglichen Kanten, d.h. nicht jede Ecke ist mit jeder anderen Ecke durch eine Kante verbunden.
Vollständiger Graph
Man bezeichnet einen Graph als vollständig, wenn alle Ecken miteinander durch eine Kante verbunden sind. Man spricht auch von einem Simplex. Zu beachten ist, dass Ecken nicht mit sich selbst durch Kanten verbunden werden müssen.
Ungewichteter Graph
Bei ungewichteten Graphen besitzen die Kanten keine Gewichte, d.h. die Gewichtung einer Kante spielt für diesen Graph keine Rolle.
Gewichteter Graph
Ein Graph kann als gewichtet bezeichnet werden, wenn seine Kanten Zusatzinformationen enthalten. So wird beispielsweise einer Kante eine Zahl zugeordnet, die Entfernungen oder Kosten repräsentiert. Sowohl gerichtete als auch ungerichtete Graphen können gewichtet sein. Der Graph $G = (V,E)$ wird durch die Funktion zum gewichteten Graph. Die Kante $[a,b]$ besitz das Gewicht, welches durch
bezeichnet wird.
Netzwerke
Erfüllt ein Graph die Eigenschafte eines gewichteten und gerichteten Graphens, so kann er als Netzwerk bezeichnet werden.
Baum
Ein Graph wird Baum genannt, falls er zusammenhängend ist und keinen Kreis enthält. Zusammenhängend ist ein Graph, wenn es zu jedem Paar $(e_i,e_j)$ einen Kantenzug gibt, der $e_i$ und $e_j$ verbindet.
Aufgabe
Erstellen Sie einen ungerichteten Graph mit $V = \{A,B,C,D,E\}$. Die Kanten sollen so gewählt werden, dass es sich um einen ungerichteten, vollständigen Graph handelt. Geben Sie nun die Kantenmenge $K$ an.
Aufgabe
Der fertige Graph aus der letzten Aufgabe dient als Grundlage für diese Aufgabe. Der Graph soll zu einem gerichteten Graph verändert werden. Geben Sie die Ecken- und Kantenmenge an.
Aufgabe
Der fertige Graph aus der letzten Aufgabe dient als Grundlage für diese Aufgabe. Entfernen Sie die Kanten, welche die Ecken $A$ und $D$, sowie $B$ und $C$ verbinden. Gesucht sind die Ecken- und Kantenmenge. Wie viele Kanten wurden entfernt und wie viele wären es bei einem ungerichteten Graph? Sind die Eigenschaften vollständig, ungerichtet, ungewichtet und Netzwerk erfüllt?
Aufgabe
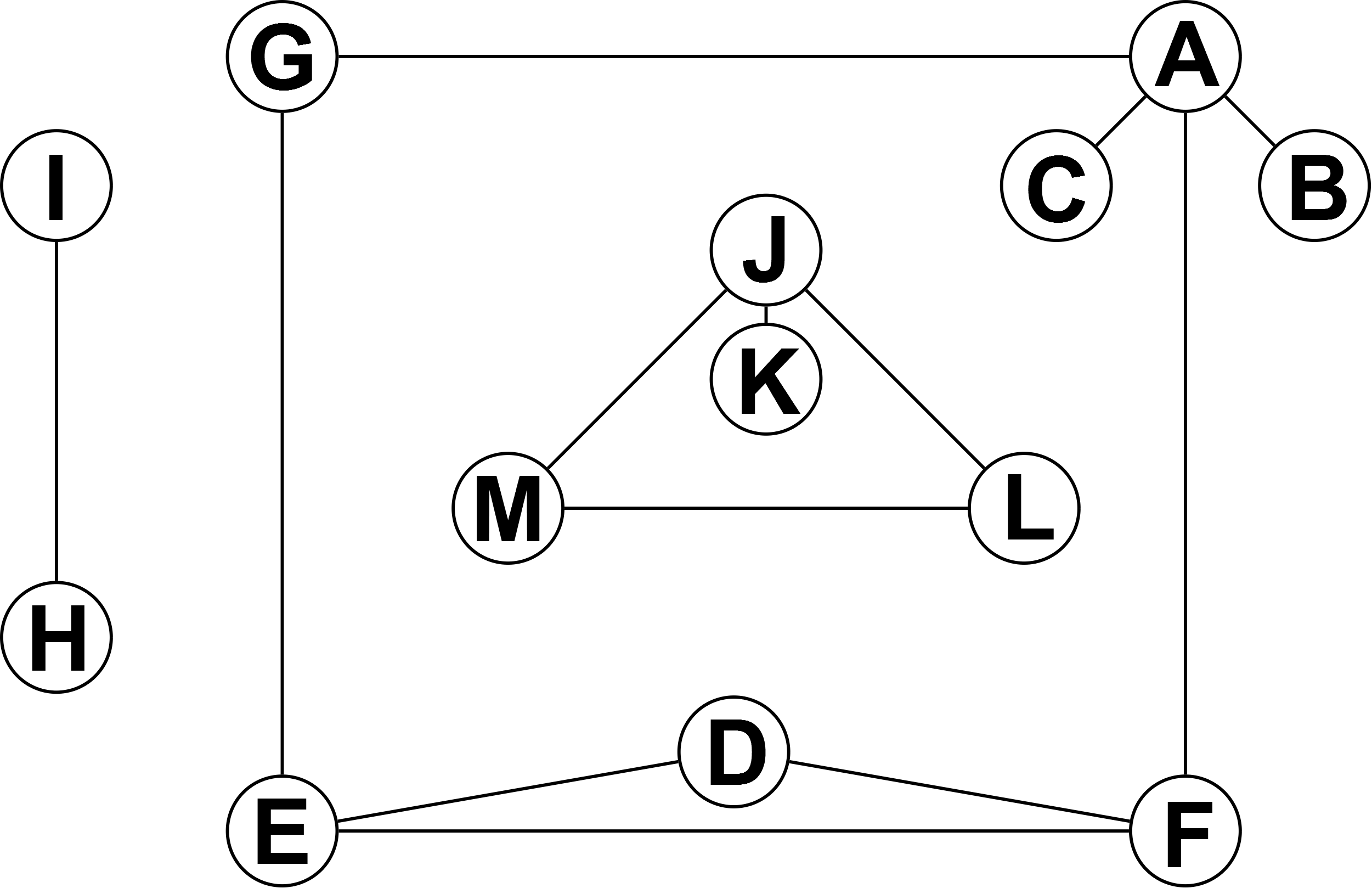
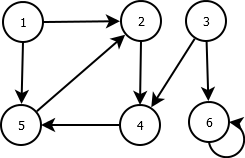
Welcher Unterschied ist bei den beiden Graphen G und H festzustellen?
Operationen für Graphen
Zugriff auf Informationen des Graphen
Der Zugriff auf Informationen von Ecken und Kanten spielt in der Graphentheorie eine große Rolle. Ohne Informationen, die mit den Kanten und Ecken verknüpft sind, wäre die Repräsentation mit Hilfe von Graphen unnütz. Kanten können beispielsweise Informationen, wie die Entfernung zwischen zwei Ecken enthalten. Man spricht dabei vom Gewicht einer Kante und von gewichteten Graphen. Da sowohl Ecken als auch Kanten oft in der Praxis als Objekte dargestellt werden, fällt es leicht Informationen anzuhängen, d.h. als Teil des Objektes zu speichern. Unter der Annahme, dass $V = 1,...,n$, könnte man die entsprechenden Informationen der Ecken in Arrays speichern. Alternativ bietet sich auch ein Hashtable statt eines Arrays an. Zugriffe können somit in konstanter Zeit abgearbeitete werden.
Die Navigation im Graphen kann man erleichtern, wenn jeder Ecke die ein- und ausgehende Kante bekannt ist. Es sit oft sinnvoll diese Informationen in der Ecke zu speichern.
Kantenqueries
Ein Eckenpaar stellt gleichzeitig die entsprechende Kante dar. Man kann sich also die Frage stellen, ob die zugehörige Kante existiert. Mit Hilfe eines Hashtables kann dies stets implementiert werden, doch solche Operationen wären entsprechend langsam. Eine effizientere Möglichkeit ist das Speichern der Umkehrkante einer gerichteten Kante, falls diese existiert. Durch das Hinzufügen eines weiteren Zeigers, welcher die Kante mit ihrer Umkehrkante verknüpft.
Erstellung, Umwandlung, Ausgabe
Um algorithmische Probleme zu lösen, sind Graphen sehr gut geeignet. Falls man eine Repräsentation gewählt hat, die für das aktuelle Problem nicht gut geeignet ist, kann man diese Graphenform stets in eine andere Form überführen. Dies ist in linearer Zeit möglich.
Aktualisierung
Das Hinzufügen oder Entfernen von Kanten und Ecken kann Algorithmen beschleunigen, weshalb solche Operationen sinnvoll sind.
Unsortierte Kantenabfolge
Die wahrscheinlich einfachste Methode Graphen zu repräsentieren, ist das Aufzählen aller Kanten. Die Kanten werden ungeordnet aufgeschrieben und beinhalten dabei das Eckenpaar, das sie verbinden. Das Gewicht der Kante kann zusätzlich gespeichert werden. Für die Wahrnehmung des Menschen ist diese Form der Graphrepräsentation nicht übersichtlich genug, denn schon bei etwas größeren Graphen geht der Überblick schnell verloren. So ist zum Beispiel die Information, ob es sich um einen gerichteten oder ungerichteten Graphen handelt bei großen Graphen schwer zu ermitteln, da die Kanten ungeordnet vorliegen.
Trotzdem wird diese Graphrepräsentation häufig für Ein- und Ausgaben genutzt. Die einzelnen Operationen können größtenteils in abgearbeitet werden. Dies ist jedoch sehr langsam und deshalb für große Graphen ungeeignet. Die nachfolgenden Repräsentationen arbeiten mit einer geordneten Reihenfolge.
Adjazenzfelder - Statische Graphen
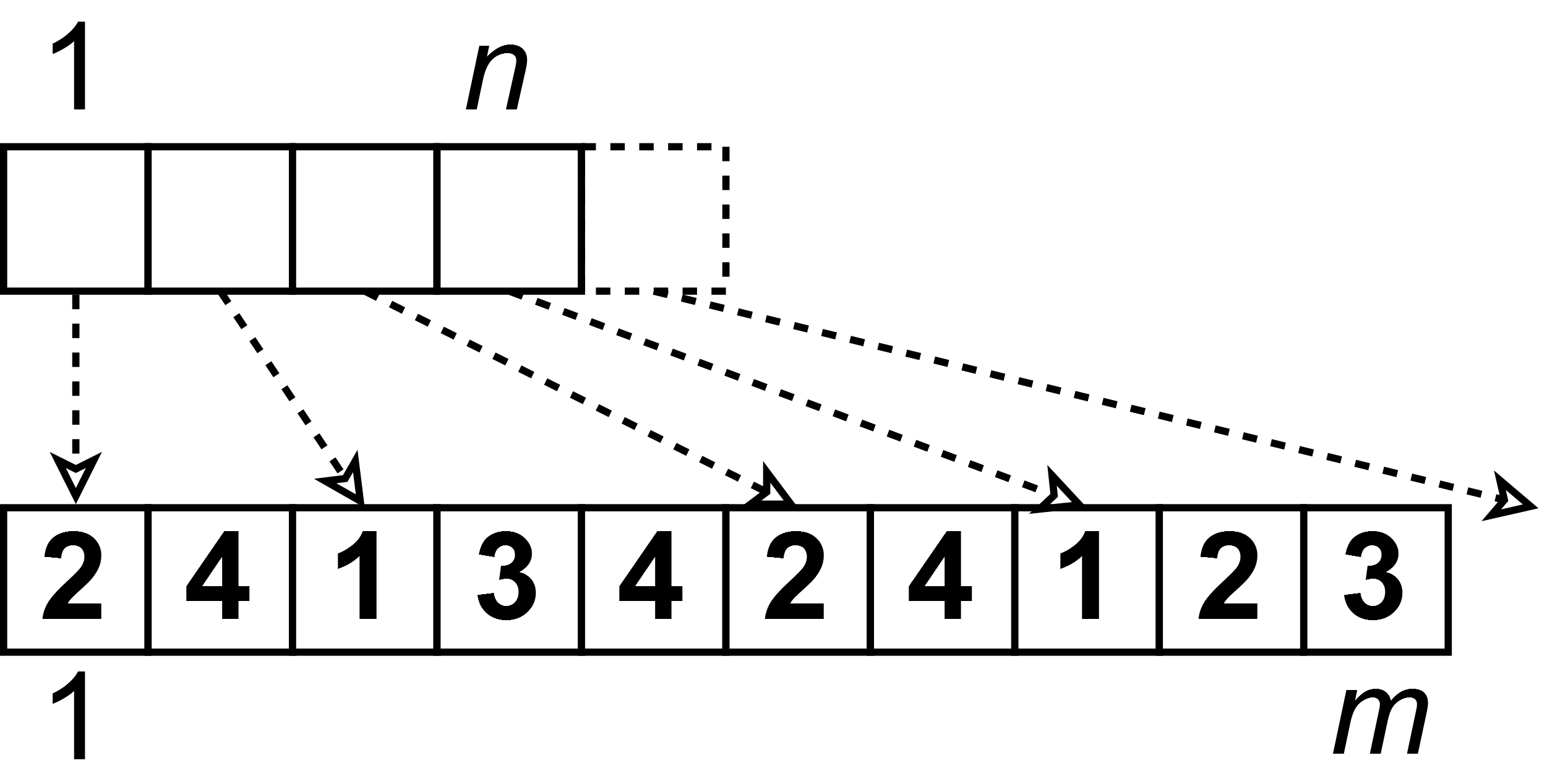
Um einen einfachen Zugriff auf die Kanten, die eine Ecke verlassen zu gewährleisten, ist es sinnvoll diese Kanten in einem Array zu sichern. Ohne Gewichte enthält dieses Array nur die Indizes der "Zielecken". Damit nicht jede Ecke ein eigenes Array für die "Zielecken" nutzt, ist es für statische Graphen nützlich all diese Informationen in einem Array zu sichern. Dieses Hauptarray soll $E$ heißen. Um die Startpositionen der Unterarrays zu speichern, erstellt man ein kleineres Array $V$. Dieses zeigt dann für jede Ecke auf die Startposition im Hauptarray $E$ und gibt somit die Informationen über die Kanten preis.
Jede Kante der Ecke $v$ kann somit durch $E[V[v]]$ erreicht werden.
Auffällig ist der geringere Speicherverbrauch dieser Graphrepräsentation, der bei $n + m$ liegt. Es ist also deutlich kompakter als bei der ungeordneten Kantenabfolge, bei der der Speicherverbrauch bei $2m$ lag.
Will man weitere Informationen speichern, ist es möglich weitere Array hinzuzufügen, die diese Informationen aufnehmen.
Adjazenzliste - Dynamische Graphen
Arrays sind kompakte und effiziente Graphrepräsentationen, mit der Ausnahme des Hinzufügens oder Löschens einer oder mehrerer Kante(n). Für solche Fälle ist der Rechenaufwand recht hoch. Will man beispielsweise eine Kante hinzufügen, so muss man alle Kanten rechts dieser neuen Kante um eine Stelle nach rechts verschieben.
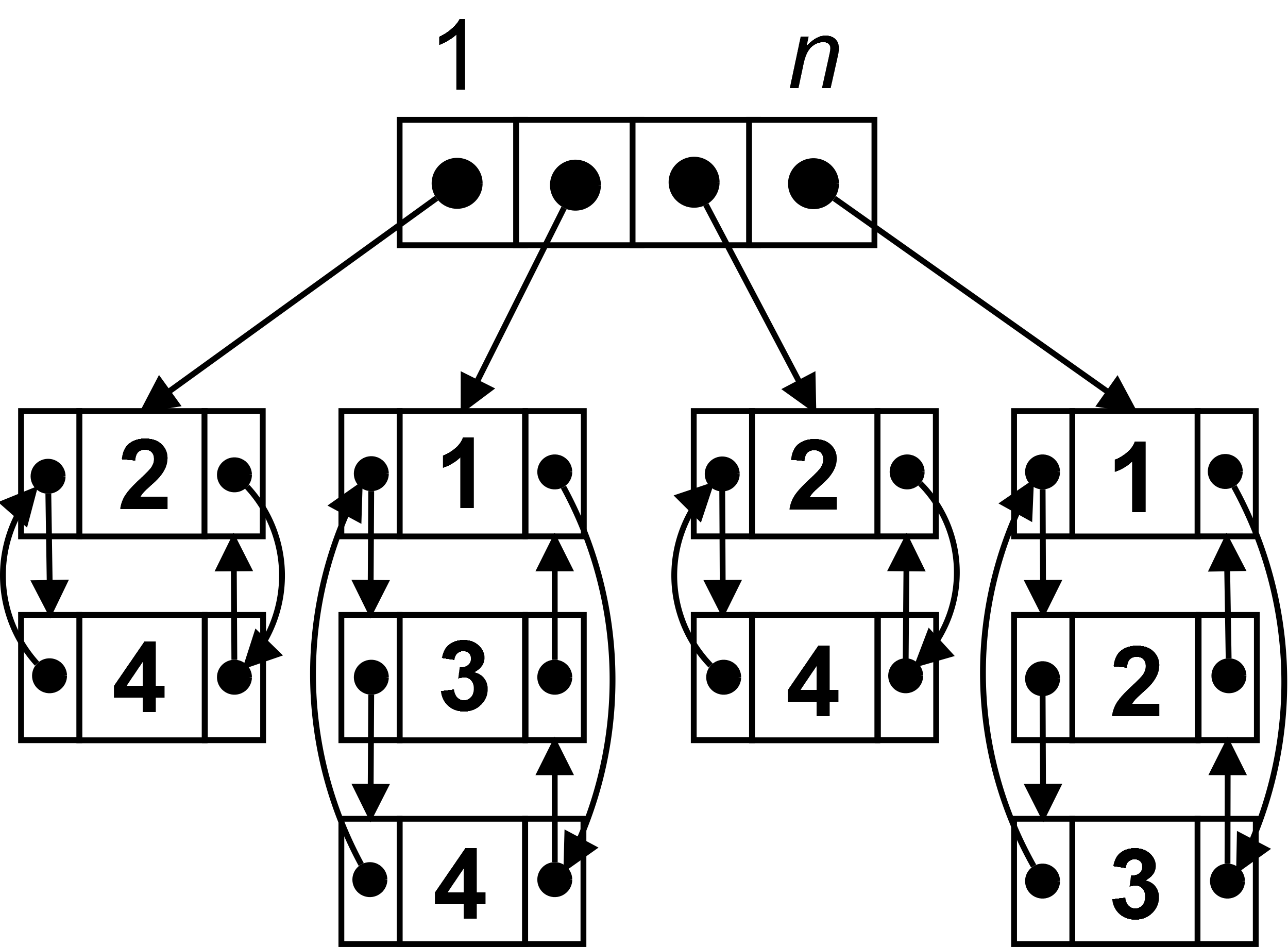
Für solche dynamischen Graphen ist eine Adjazenzliste vorteilhaft, die für jede Ecke $v$ eine Abfolge $E_v$ der ein- und ausgehenden Kanten durch eine verkettete Liste oder ein ungebundenes Array repräsentiert.
In einer einfach verketteten Liste erhält jede Ecke eine Liste mit den Nachfolgern bei einem gerichteten Graph beziehungsweise mit den Nachbarn bei ungerichteten Graphen.
Adjazenzmatrix
Eine Darstellungsweise für Graphen ist die Darstellung als Adjazenzmatrix. Diese Matrix besteht aus einem mal
großen Feld mit booleschen Variablen, in der
auf 1 oder true gesetzt wird, wenn von Knoten
zu Knoten
eine Kante vorhanden ist und auf 0 oder false wenn eine solche Kante nicht existiert.
Unabhängig von der Kantenanzahl, benötig die Adjazenzmatrix eines Graphen Speicherplatz
. Unter Beachtung der Symmetrie bezüglich der Hauptdiagonale der Adjazenzmatrix des Graphen G definiert man die Transponierte einer Matrix
als die Matrix
mit
In einem ungerichteten Graphen repräsentieren und
die gleiche Kante, nämlich genau die Kante, die
und
verbindet.
Das heißt, die Adjazenzmatrix A für einen ungerichteten Graphen ist gleich ihrer Transponierten. Es gilt $ A = A^T$.
Es ist so möglich, nur die Einträge über der Hauptdiagonale der Adjazenzmatrix zu Speichern und somit den erforderlichen Speicherbedarf zu halbieren.
Es sei ein Graph mit von 1 bis
durchnummerierter Knoten gegeben.
Die Dazugehörige Adjazenzmatrix besteht aus:
- $\left( \begin{array}{ccc} a_{11} & \cdots & a_{1j} \\ \vdots & \ddots & \vdots \\ a_{i1} & \cdots & a_{ij} \end{array} \right) $allgemein
- $\left( \begin{array}{ccccc} 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 \\ \end{array} \right) $ungerichtet
- $\left( \begin{array}{cccccc} 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) $gerichtet
---
---
Aufgabe
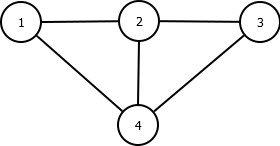
Erstellen Sie die zu den Graphen passenden Adjazenzmatrizen!
Aufgabe
Stellen Sie den zur Adjazenzmatrix passenden Graphen dar!
$\left(
\begin{array}{cccc}
0&1&0&1\\
1&0&1&1\\
0&1&0&1\\
1&1&1&0\\
\end{array}
\right)
$
Inzidenzmatrix
Neben der Adjazenzmatrix, kann auch eine Inzidenzmatrix zur Darstellung eines Graphen im Computer verwendet werden.
Diese beschreibt einen Graphen indem sie Knoten, welche mit Kanten inzident sind, angibt.
Ein Graph mit Knoten und
Kanten wird dann durch eine
x
-Matrix repräsentiert.
Die Knoten werden von
bis
und die Kanten von
bis
nummeriert und die Beziehungen der Knoten zu den Kanten in die Matrix eingetragen.
Jede Spalte der Inzidenzmatrix enthält genau zwei Einträge die sich von 0 unterscheiden.
Der ungerichtete Graph mit
und
ist Inzidenzmatrix mit den Elementen
- $\left( \begin{array}{ccccccc} 1 & 0 & 0 & 0 & 1 & 0 & 0\\ 1 & 1 & 0 & 0 & 0 & 1 & 1\\ 0 & 1 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 1 & 0 & 0 & 1\\ 0 & 0 & 0 & 1 & 1 & 1 & 0\\ \end{array} \right) $
Der gerichteten, schleifenfreien Graph mit
und
ist Inzidenzmatrix mit den Elementen
- $\left( \begin{array}{ccccccc} 1 & 0 & 0 & 0 & 1 & 0 & 0\\ -1 & 1 & 0 & -1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 1\\ 0 & 0 & -1 & 1 & 0 & 0 & 0\\ 0 & -1 & 1 & 0 & -1 & -1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & -1\\ \end{array} \right) $
Laufzeitvergleich
| Adjazenzmatrix | Inzidenzmatrix | |
| Speicherbedarf | | |
| Knoten hinzufügen | | |
| Kante hinzufügen | | |
| Knoten entfernen | | |
| Kante entfernen | | |
| Nachbarabfrage | | |
| Bemerkungen | Langsames Hinzufügen und Entfernen von Knoten Matrix muss kopiert und die Größe angepasst werden | Langsames Hinzufügen und Entfernen von Knoten und Kanten Matrix muss kopiert und die Größe angepasst werden |
Anwendungsgebiete
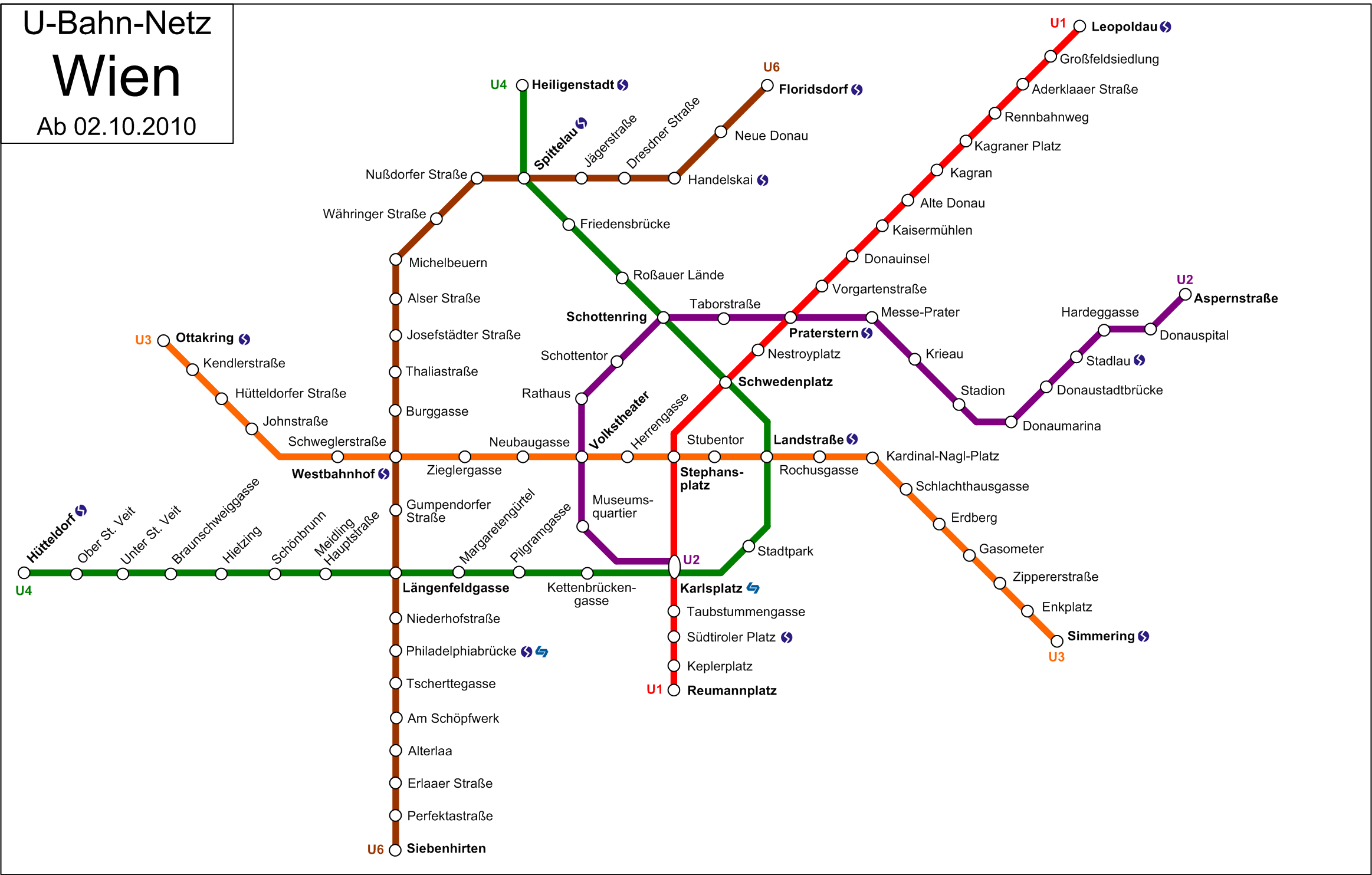
Graphen finden häufig Anwendung bei komplexen Netzen. So kann man beispielsweise das Verkehrsnetz einer U-Bahn als Graph darstellen. Jede Station stellt eine Ecke dar und die Verbindungen zwischen den Stationen sind Kanten. Einen solchen Graph kann man auch gewichten, indem man die Fahrzeit von Station zu Station, also entlang der Kanten hinzufügt.
Aufgabe
Ermitteln Sie den kleinsten Kreis des Graphen "Wiener U-Bahn-Netz" und geben Sie dessen Ecken- und Kantenmenge an. Handelt es sich hierbei um einen zusammenhängenden Graphen?
Weiterhin werden Graphen im Bereich der Routenplanung von Kartendiensten genutzt, um Wege zu berechnen, die kurz, zeiteffizient und möglichst ohne Hindernisse (Stau, Baustellen) sind.
Aufgabe
Wie könnte das Straßennetz einer Stadt in einen Graphen umgewandelt werden und wie ist möglich dann die kürzeste Route zu bestimmen?
So wie diese Verkehrsnetze können auch elektrische Netze oder Telefonnetze durch Graphrepräsentation dargestellt werden.
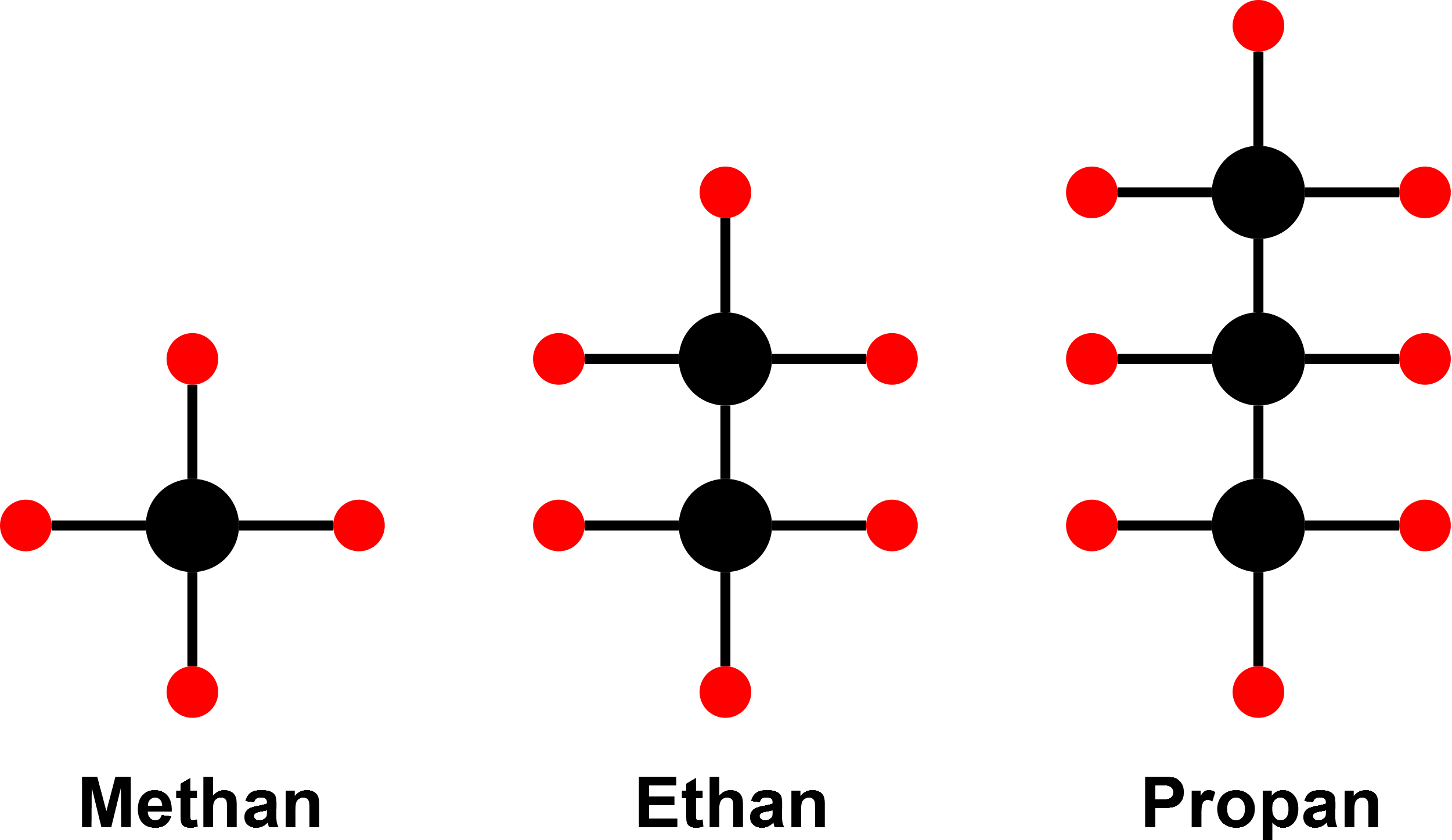
In der Chemie treten bei organischen Stoffen Isomere auf. Isomerie beschreibt den ähnlichen atomaren Aufbau von Molekülen, die aber andere Eigenschaften aufweisen. Dies tritt zum Beispiel bei den Alkanen (siehe Bild) auf. Diese können als spezielle Graphenart, den Bäumen repräsentiert werden.
In der theoretischen Informatik nutzt die Automatentheorie Graphen als grafische Darstellungsform für NEAs und DEAs. Hier tritt häufig der sonst seltene Fall auf, dass Schlingen im Graph vorzufinden sind. Automaten sind jedoch stets gerichtete Graphen, was in ihrer Zustandsänderung begründet ist. Durch diese Darstellungsvariante kann man sich die Arbeitsweise eines Automaten besonders gut vor Augen führen.
Literatur
- www.mpi-inf.mpg.de/~mehlhorn/ftp/Toolbox/GraphRep.pdf
- Algorithmen - Eine Einführung 2. Auflage Th.H.Cormen | Ch.E. Leiserson | R.Rivest | C.Stein (Oldenbourg)
- Robert Sedgewick - Algorithmen (Addison-Wesley)
- Karsten Morisse - Podcast Algorithmen & Datenstrukturen Fachhochschule Osnabrück