Empirische Analyse
Aus ProgrammingWiki
Weiß man zu wenig über den Entwurf eines (z.B. als ausführbares Programm) vorliegenden Algorithmus', so ist es oft nicht möglich, dessen Aufwand mit analytischen Methoden zu bestimmen. Dann hilft eine empirische Analyse. Dabei misst man, wie lange der Algorithmus zur Berechnung der gesuchten Resultate benötigt, und versucht einen funktionalen Zusammenhang $T: n\mapsto T(n)$ herauszufinden.
Die empirische Analyse macht es notwendig, $k$ Messungen mit unterschiedlichen Eingaben gleicher Größe $n$ durchzuführen. Man betrachtet verschiedene Probleminstanzen, z.B. $k=10$, für jeden betrachteten Wert ein und derselben Problemgröße, z.B. $n=100,1000,10000,100000,1000000$.
Zur Auswertung kann man für jedes $n$ das arithmetische Mittel der $k$ vorlegenden Messwerte, nehmen. Dies liefert den Aufwand im mittleren Fall (average case). Nimmt man den jeweils größten/kleinsten Wert, ergibt sich der Aufwand im schlechtesten bzw. besten Fall (worst/best case).
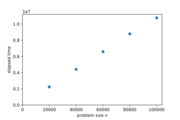
Zur grafischen Darstellung kann man die gemittelten Werte in einem Streudiagramm (scatter plot) eintragen.
Inhaltsverzeichnis |
Regression
Ein solches Streudiagramm lässt den funktionalen Zusammenhang oft schon erahnen. Besser ist es, wenn wir objektiv(!), d.h. mit mathematischen Mitteln, eine Funktion bestimmen, die den Zusammenhang zwischen $n$ und $T(n)$ ausdrückt. Dies entspricht dem Hineinlegen einer Kurve, die dem Punkteverlauf möglichst gut folgt und Ausreißer geeignet verarbeitet.
Diese Technik wird Regression genannt. Am besten ist es, wenn man eine Gerade verwenden kann. Man spricht von linearer Regression. Dies gilt zunächst natürlich nur für lineare Zusammenhänge zwischen $n$ und $T(n)$. Vermutet man eine Polynom- oder Exponentialfunktion, so kann man die Messwerte in vielen Fällen so aufbereiten (umrechnen), dass die daraus gewonnenen Daten durch eine lineare Funktion approximiert werden können. Eine entsprechende Rückrechnung liefert dann die konkreten Koeffizienten der gesuchten Funktion.
Lineare Regression
Wie oben angekündigt, suchen wir eine geeignete lineare Funktion $f:\mathbb{N}\mapsto\mathbb{R}$. Sie ist wie folgt definiert:
$$ f(x) = a \cdot x + b \text{ mit $a, b \in \mathbb{R}$} $$
Nun geht es darum, $a$ und $b$ so zu wählen, dass der Verlauf der Gerade möglichst gut mit dem Verlauf der Punkte übereinstimmt. Das ist der Fall, wenn
$$ \Sigma_{i=0}^{n}|f(x_i)-y_i|=\Sigma_{i=0}^{n}|a\cdot x_i + b - y_i|\rightarrow min. $$
- $x_i$ : $x$-Wert des $i$-ten Punktes
- $y_i$ : $y$-Wert des $i$-ten Punktes
Eine von Null verschiedene Differenz kann entweder positiv oder negativ sein, je nachdem ob der Punkt oberhalb oder unterhalb der Geraden liegt. Da aber nur die Entfernung des jeweiligen Punktes von der Geraden aufsummiert wird, bildet man den absoluten Betrag der betrachteten Differenz.
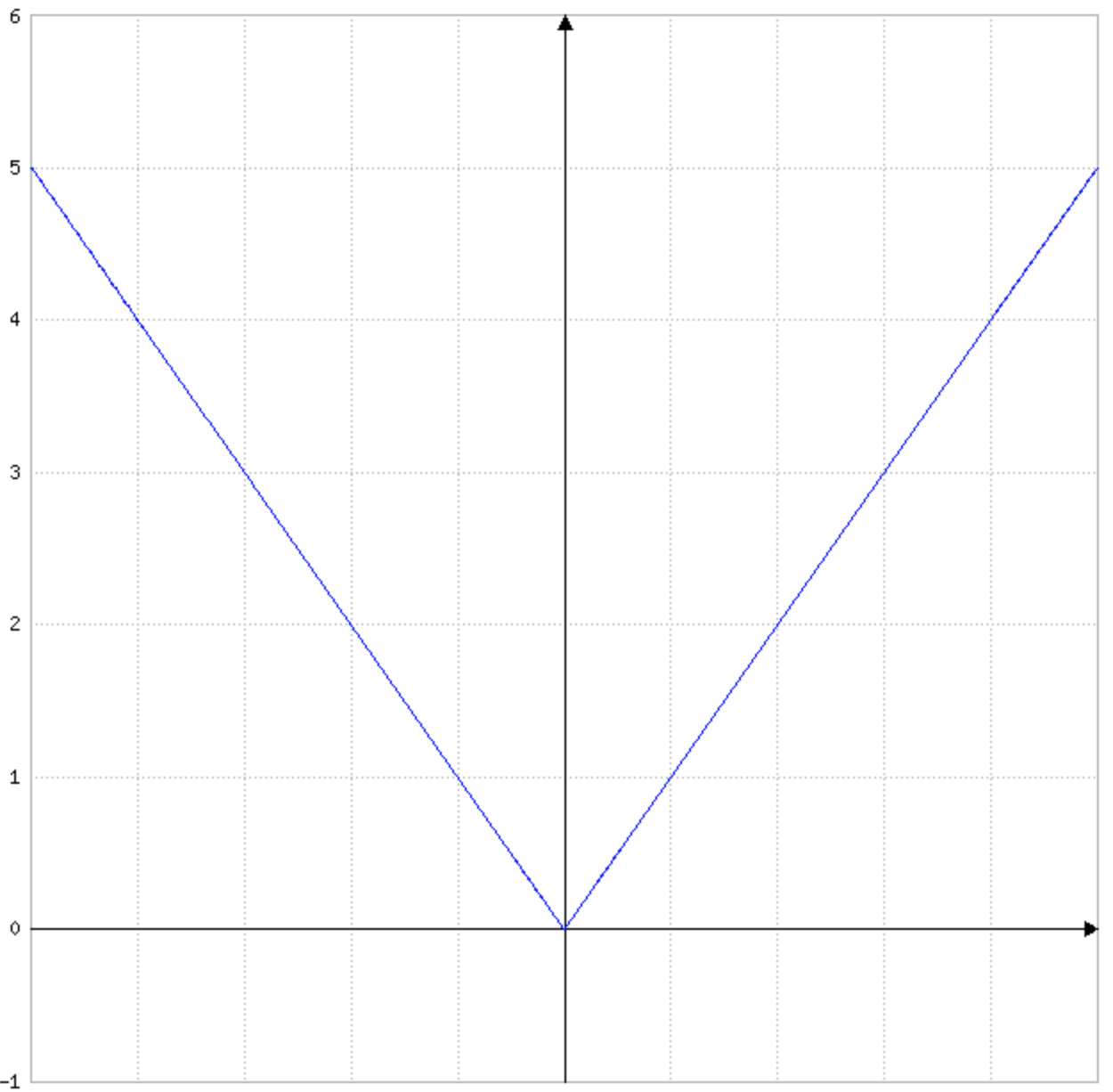
Zur Berechnung des globalen Minimums muss die oben angegebene Summe abgeleitet werden, um die resultierende Ableitung gleich Null zu setzen. Die Betragsfunktion ist jedoch an der Stelle $x=0$ nicht differenzierbar, was man in dem zugehörigen Graph (rechts, als Thumbnail) an der "Spitze" erkennt. Wie soll da eine Tangente angelegt werden?
Nimmt man die Entfernungsquadrate, sind die einzelnen Differenzen betragsmäßig berücksichtigt, denn es gibt keine negativen Werte. Außerdem kann die quadratische Funktion problemlos abgeleitet werden, sodass man das Minimum der Ausgangsfunktion leicht berechnen kann (Methode der kleinsten Quadrate nach Gauss). Die Summe der Entfernungsquadrate aller Punkte von der Geraden soll möglichst klein sein (Optimierungsziel).
$$ e(a, b) = \sum_{i=1}^n (a \cdot x_i + b - y_i)^2 $$
Das Minimum lässt sich analytisch bestimmen, indem man die partiellen Ableitungen von $e(a, b)$ bildet und diese gleich 0 setzt.
$$ \begin{align*} e(a, b) & = \sum_{i=1}^n \left((a x_i + b)^2 - 2 \cdot (a x_i + b) \cdot y_i + y_i^2\right) \\ & = \sum_{i=1}^n \left(a^2 x_i^2 + 2 a x_i b + b^2 - 2 a x_i y_i - 2 b y_i + y_i^2\right) \\ \frac{\partial e(a, b)}{\partial a} & = \sum_{i=1}^n \left(2 x_i^2 a + 2 x_i b - 2 x_i y_i\right) \\ & = 2 \sum_{i=1}^n \left(x_i^2 a + x_i b - x_i y_i\right) \\ & = 2 \left( \sum_{i=1}^n x_i^2 a + \sum_{i=1}^n x_i b - \sum_{i=1}^n x_i y_i \right) \\ & = 2 a \sum_{i=1}^n \left(x_i^2 + b \sum_{i=1}^n x_i - \sum_{i=1}^n x_i y_i \right) \\ \frac{\partial e(a, b)}{\partial b} & = \sum_{i=1}^n \left(2 a x_i + 2 b - 2 y_i\right) \\ & = 2 \sum_{i=1}^n \left(a x_i + b - y_i\right) \\ & = 2 \left( \sum_{i=1}^n a x_i + \sum_{i=1}^n b - \sum_{i=1}^n y_i \right) \\ & = 2 \left( a \sum_{i=1}^n x_i + n b - \sum_{i=1}^n y_i \right) \\ \end{align*} $$
Nun müssen die partiellen Ableitungen gleich 0 gesetzt werden.
Im folgenden werden $\overline{x}$ als das arithmetische Mittel von $x$ : $\overline{x} = \frac{\sum_{i=1}^n x_i}{n}$ und $\overline{y}$ als das arithmetische Mittel von $y$ : $\overline{y} = \frac{\sum_{i=1}^n y_i}{n}$ bezeichnet.
$$ \left\{ \begin{array}{c} \begin{align*} 2 \left( a \sum_{i=1}^n x_i^2 + b \sum_{i=1}^n x_i - \sum_{i=1}^n x_i y_i \right) & = 0 \\ 2 \left( a \sum_{i=1}^n x_i + n b - \sum_{i=1}^n y_i \right) & = 0 \end{align*} \end{array} \right. $$
$$ \left\{ \begin{array}{c} \begin{align*} a \sum_{i=1}^n x_i^2 + b \sum_{i=1}^n x_i - \sum_{i=1}^n x_i y_i & = 0 \\ a \sum_{i=1}^n x_i + n b - \sum_{i=1}^n y_i & = 0 \end{align*} \end{array} \right. $$
$$ \left\{ \begin{array}{c} \begin{align*} a \sum_{i=1}^n x_i^2 + b \sum_{i=1}^n x_i & = \sum_{i=1}^n x_i y_i \\ a \sum_{i=1}^n x_i + nb & = \sum_{i=1}^n y_i \end{align*} \end{array} \right. $$
$$a \sum_{i=1}^n x_i + nb = \sum_{i=1}^n y_i $$ $$\iff b = \frac{\sum_{i=1}^n y_i - a \sum_{i=1}^n x_i}{n} \iff b = \overline{y} - a \overline{x}$$ $$\implies a \sum_{i=1}^n x_i^2 + \frac{\sum_{i=1}^n y_i - a \sum_{i=1}^n x_i}{n} \sum_{i=1}^n x_i = \sum_{i=1}^n x_i y_i$$ $$\iff a \sum_{i=1}^n x_i^2 + \frac{\sum_{i=1}^n x_i \sum_{i=1}^n y_i}{n} - a \frac{\left( \sum_{i=1}^n x_i \right)^2}{n} = \sum_{i=1}^n x_i y_i$$ $$\iff a \sum_{i=1}^n x_i^2 - a \frac{\left( \sum_{i=1}^n x_i \right)^2}{n} = \sum_{i=1}^n x_i y_i - \frac{\sum_{i=1}^n x_i \sum_{i=1}^n y_i}{n}$$ $$\iff a \left( \sum_{i=1}^n x_i^2 - \frac{\left( \sum_{i=1}^n x_i \right)^2}{n} \right) = \sum_{i=1}^n x_i y_i - \frac{\sum_{i=1}^n x_i \sum_{i=1}^n y_i}{n}$$ $$\iff a = \frac{\sum_{i=1}^n x_i y_i - \frac{\sum_{i=1}^n x_i \sum_{i=1}^n y_i}{n}}{\sum_{i=1}^n x_i^2 - \frac{\left( \sum_{i=1}^n x_i \right)^2}{n}}$$ $$\iff a = \frac{\sum_{i=1}^n x_i y_i - \frac{n \cdot \overline{x} \cdot n \cdot \overline{y}}{n}}{\sum_{i=1}^n x_i^2 - \frac{n \cdot \overline{x} \cdot n \cdot \overline{x}}{n}}$$ $$\iff a = \frac{\sum_{i=1}^n x_i y_i - n \cdot \overline{x} \cdot \overline{y}}{\sum_{i=1}^n x_i^2 - n \cdot \overline{x}^2}$$
Nun hat man mit
$$ a = \frac{\sum_{i=1}^n x_i y_i - n \cdot \overline{x} \cdot \overline{y}}{\sum_{i=1}^n x_i^2 - n \cdot \overline{x}^2} $$
und
$$ b = \overline{y} - a \overline{x} $$
Formeln, mit denen man die beiden Koeffizienten der linearen Funktion bestimmen kann.
Exponentielle Regression
Bei der exponentiellen Regression möchte man eine Exponentialfunktion finden, die sich möglichst gut an die gegebenen Punkte anschmiegt. Dieses Problem lässt sich auf lineare Regression zurückführen, indem man die y-Achse logarithmisch anlegt. Wir bezeichnen diese als y'-Achse. Eine Exponentialfunktion wird hier durch eine Gerade dargestellt. Deshalb lässt sich das bereits bekannte Verfahren der linearen Regression anwenden.
Wählt man als Basis $2$, so möchte man eine Funktion der Form $f(x) = a \cdot 2^{bx}$ finden. Logarithmiert man die Funktionsgleichung auf beiden Seiten, so erhält man:
$$ \begin{align*} \log_2 \left(f(x) \right) & = \log_2 \left(a \cdot 2^{bx} \right) \\ y' & = \log_2 a + \log_2 2^{bx} \\ y' & = \log_2 a + bx \end{align*} $$
Es handelt sich um eine lineare Funktion, deren Anstieg $b$ und Schnittpunkt mit der $y'$-Achse $\log_2 a$ lassen sich wie oben beschrieben bestimmen.
Polynomielle Regression
Bei der polynomiellen Regression möchte man eine Funktion der Form $f(x) = a \cdot x^k$ finden, die die Punkte möglichst gut annähert. Deshalb müssen Konstanten $a$ und $k$ gefunden werden, für die der Fehler minimal ist.
Hierfür wird wieder das Logarithmieren der Achsen benutzt. Jedoch wird hier nicht nur die y-Achse, sondern auch die x-Achse logarithmiert. Die Basis des Logarithmus ist frei wählbar, es muss sich jedoch bei der $x'$- und $y'$-Achse um die gleiche Basis handeln.
Beispiele:
Durch Logarithmieren der y-Achse erhält man $y'$:
$$ \begin{align*} f(x) &= a \cdot x^k \\ \implies \log(f(x)) &= \log(a \cdot x^k) \\ \implies \log(f(x)) &= k \log(x) + \log(a) \end{align*} $$
Setzt man nun die x-Achse (mit $x'$ gekennzeichnet) $x' = \log(x)$, so erhält man eine Gerade. $\log(a)$ gibt den y-Achsenschnittpunkt und $k$ den Anstieg der Geraden an.
$$ \begin{align*} f(x) &= a \cdot x^k \\ \implies \log(f(x)) &= \log(a \cdot x^k) \\ \implies \log(f(x)) &= k \log(x) + \log(a)\\ \implies y' &= k x' + \log(a) \end{align*} $$
Nun kann man wie bei der linearen Regression vorgehen und $k$ und $\log(a)$ bestimmen.
Korrelationskoeffizient
Der Pearson-Korrelationskoeffizient $r$ ist ein Maß für die Beziehung zwischen zwei Variablen. Im Zusammenhang der linearen Regression kann er genutzt werden, um die Qualität der Regressiongerade zu bestimmen.
$$r = \frac{cov(X, Y)}{\sigma_X \sigma_Y}$$
$cov(X, Y)$ ist die Kovarianz von $X$ und $Y$ und wird folgendermaßen bestimmt: $$cov(X, Y) = \frac{1}{n} \sum_{i=1}^n (x_i - \overline{x}) (y_i - \overline{y})$$
Hinweis: Für die Kovarianz zwischen zwei Zufallsvariablen $X$ und $Y$ findet man auch eine Definition, die sich von der obigen im Nenner unterscheidet: Steht dort $n-1$, so verwendet man die sog. Bessel-Korrektur. In praktischen Anwendungen geschieht das oft, um anstelle der Kovarianz der Population die Stichprobenkovarianz zu berechnen. Die Verwendung dieser beiden Definitionen setzt sich bei der Berechnung der Standardabweichung fort. Für unsere Betrachtung ist eine Entscheidung für die eine oder andere Definition eher nebensächlich, da wir uns prinzipiell für die Qualität der Regressionsgerade interessieren. Deshalb verwenden wir nur das $n$ im Nenner.
Eingesetzt ergibt sich für $r$ folgende Formel:
$$r = \frac{\frac{1}{n} \sum_{i=1}^n (x_i - \overline{x}) (y_i - \overline{y})}{\sqrt{\frac{1}{n} \sum_{i=1}^n (x_i - \overline{x})^2} \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i - \overline{y})^2}}$$
$$r = \frac{\sum_{i=1}^n (x_i - \overline{x}) (y_i - \overline{y})}{\sqrt{\sum_{i=1}^n (x_i - \overline{x})^2} \sqrt{\sum_{i=1}^n (y_i - \overline{y})^2}}$$
Laut der Cauchy-Schwartz-Ungleichung gilt:
$$\left| \sum_{i=1}^n (x_i - \overline{x}) (y_i - \overline{y}) \right|^2 \leqslant \sum_{i=1}^n (x_i - \overline{x})^2 \sum_{i=1}^n (y_i - \overline{y})^2 \implies \sum_{i=1}^n (x_i - \overline{x}) (y_i - \overline{y}) \leqslant \sqrt{\sum_{i=1}^n (x_i - \overline{x})^2} \sqrt{\sum_{i=1}^n (y_i - \overline{y})^2} \implies \left| r \right| \leqslant 1 \implies -1 \leqslant r \leqslant 1$$