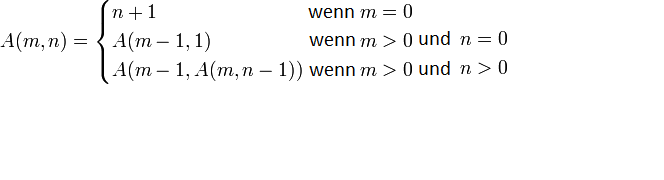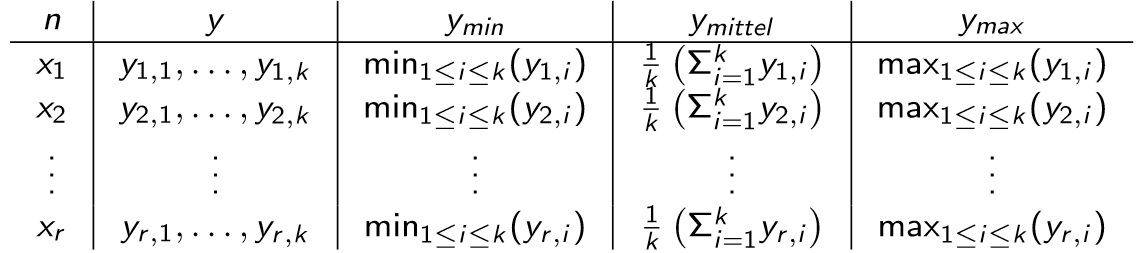Einführung WS13-14
Aus ProgrammingWiki

Oliver Krüger
Inhaltsverzeichnis |
Praktische und absolut unlösbare Probleme
Das ist ein Problem, für welche existiert keine Algorithmus, der nachdem endliche Schritte antworten kann, "ja" oder "nein" für dem beliebig Einzustand.
Am bekannste Beispiel ist Halteproblem. Halteproblem ist wie eine Frage für Algorithmus, ob ein Program halten kann (in endliche Zeit). Die Frage kann nur die Anfangzustande betreffen oder auch alle mögliche Zustande. Es gibt keine universelle Algorithmus, die das Halteproblem für alle Algorithmen anmachen, aber wir können nur einbilden, wie soll diese Algorithmus aussehen.
prozedur stop(programm, daten):
wenn programm(daten) halten sich, das
züruck ja,
gegebenenfalls
züruck nein.
Beispiel - Schachmatch und Tic Tac Toe
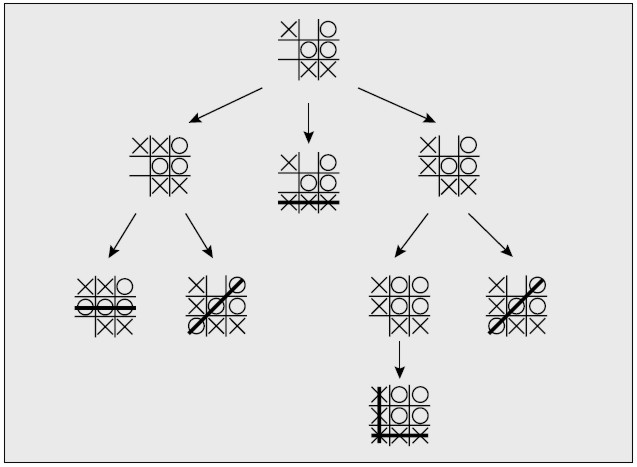
Probleme mit der Auflösung können wir in verschiedene Spiele merken. Sehr gute Beispiel auf praktisch unlösbare Probleme sind Denkspiele und die künstliche Intelligenz. Dank die Baumdiagramme können wir schauen, wie Programm planen selbste nächste Schritte in Spiel. Tic Tac Toe ist nicht so ausgebaut wie z.B. Schachmatch und dank dass, wir die Baumdiagramme aus ganz Spiele vorbereiten können. Hier haben wir klein Beispiel, ein Teil aus Spiel:
Das Programm sieht mögliche Auflösungen und wählt am beste in diese Situation aus. Schade, aber Situation mit Schachmatch oder Damespiel ist schon nicht so leicht. Damit alle mögliche in Schachmatch vorhersehen, brauchen wir sehr stark Computer und das ist nicht so praktisch Methode durch das. Deshalb können wir sagen dass, in Praktisch diese Problem ist unlösebare aber in Theorie ist das möglich. Programmen werden so geschrieben, um nur einige nächste Schritte in Zukunft vorherzusehen.
Beispiel - Ackermann-Peter-Funktion
AP Funktion nutzen oft Programmierer in Testen der Qualität den Kompilatore. Auch ist gut Beispiel auf der Berechenbarkeitstheorie. Hier steht das mathematische Ausdruck diese Funktion:
Natürlich können wir auch diese Funktion in Scheme-Prozedur schreiben:
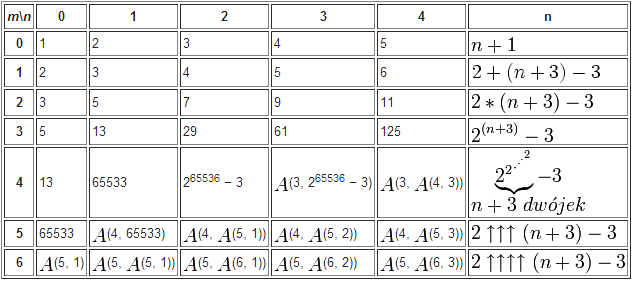
Die Ergebnis in AP Funktionen steigt sehr rapid. Für die Zahlen m=4 und n=2 beträg schon $2^{65536} - 3$.
Hier steht ein Beispiel, wie schnell die Ergebnis steigt:
Empirische Analyse
Die Methode für verschiedene Eingabewerte, welche nutzen wir bis Experimenten mit Algorithmen, heißt Zeitmessung. Aufgrund der Testen können wir nicht nur Effizienz aber auch, ob Programm wirklich richtig funktioniert. Leider, wir können nicht sagen dass, auf Comuter X, Program Y brauch W Sekunden für Einzustände ABC. Deshalb ist wichtig die Beobachtung den Rechnenschritte, d.h Grundoperationen. Der funktionalen Zusammenhang beschtecht zwischen Problemgröße n und der zugehörigen Aufwand T(n).
T(n) = f(n)
z.B.: $T(n) = r * n^{2} + k$ mit $r,k = konst, r > 0,$
Wichtig ist, dass die Werte aus welche Problemgröße nutzen, sind näturliche Zahlen größer als null.
Bit-Komplexität
Fast alle Laptops arbeiten jetzt auf Prozessoren mit 32Bit oder 64Bit. Für "normale" Nutzer ist das groß genung aber für uns (Informatiker) reicht es nicht. Die Problem ist, wenn die Einschränkung die Zeitaufwand durch Konstante ist. Sondern die Addition und Multiplikation wirken als Grundoperation, wir sprechen in diese Fall über uniformen Kompläxitätsmaß.
Uniformen Komplexität nutzt von Registermaschine.
Abrundungsfunktion und Aufrundungsfunktion (Floor and ceiling functions)
Floor und ceiling sind Funktionen in Mathematik, die Zahlen von die reellen Zahlen bis die natürliche Zahlen runden. Floor macht das bis unter die Grenze, und ceiling bis oben die Grenze.
Floor ist die größte ganze Zahl aber nicht größer als $x$:
$
\left\lfloor x \right\rfloor = max \{k \in \mathbb{Z}:\le x \}
$
Ceiling ist die kleinste ganze Zahl aber nicht kleiner als $x$: $ \left\lceil x \right\rceil = min \{k \in \mathbb{Z}:\ge x \} $
Warum brauchem wir das?
Dank floor, können wir die Länge $|z_{b}|$ zur Darstellung einer Zahl $z$ erfordelichen Wortez $z_{b}$ durch $\left\lfloor log_{b} z \right\rfloor + 1$ zeigen. Wir verwenden das mithilfe Ausdruck $ |z_{b_{1}}| = \frac{\log b_{2}}{\log b_{1}} * |z_{b_{2}}| $, damit Binärdarstellung d.h. Bit-Komplexität erhalten.
Beispiel - Multiplikation à la Russe
Das ist eine Methode der Multiplikation. Zur Berechnung nutzen wir zwei Zahlen $a$ und $b$, damit Spalten bilden. In nächste Schritte teilen wir $a$ durch 2 und mehren $b$ mit 2.
Achtung! Wenn wir ungerade Zahl teilen, müssen die neue Zahl unten runden (Floor) .
Schluss ist, wann die Zahl in $a$-Spalte bis 1 hinzukommen. In nächste Schritt müssen wir prüfen, ob Zahlen in diese Spalte ungerade oder gerade sind, wenn gerade - streichen wir diese Zeile. Die reste Zeilen, die bleiben, addieren wir die Zahlen von $b$-Spalte und die Summe ist auch Summe der Multiplikation.
52 * 32 = 1664 - streichen 26 64 - streichen 13 128 6 256 - streichen 3 512 1 1024
128 + 512 + 1024 = 1664
Scheme-Prozedur product à la Russe
Die Basisoperationen lsh und rsh sind gute Beispiel auf linear Aufwand in Bezug auf die Länge der Liste.
Prozedur my-odd benutzt auch von linear Aufwand. Prozedur zurück #t, wenn die letzte Zahl (d.h am weitesten rechts stehen)dem Listenelement 1 ist. Umgekehrt ist mit #f, wenn diese Zahl null ist.
Jetzt probieren wir eine Prozedur schreiben, aber davor verändern wir die Prozedur product, damit helper sammelt alle zu addierenden Zahlen (Bitlisten). binadd sorgt für deren Addition, wobei allbinadd die weiter unten definierte Prozedur adder verwendet. adder imitiert die Arbeit eines Volladders (Bit 1, Bit 2 und Übertrag). Die globale Variable calls wird für die Zählung der als elementar anzusehenden Adder-Operationen benötigt.
Das ist neue-alte product, jetzt product-binary:
Und unsere Prozedur bis Addierung - adder:
Hinweise, die Zeilen bedeuten: (and (= a 0)(= b 0)(= c 1)) -> 0 + 0 + 1 = (1 . 0) (and (= a 0)(= b 1)(= c 0)) -> 0 + 1 + 0 = (1 . 0) (and (= a 1)(= b 0)(= c 0))) -> 1 + 0 + 0 = (1 . 0) (and (= a 1)(= b 1)(= c 0)) -> 1 + 1 + 0 = (0 . 1) (and (= a 1)(= b 0)(= c 1)) -> 1 + 0 + 1 = (0 . 1) (and (= a 0)(= b 1)(= c 1))) -> 0 + 1 + 1 = (0 . 1)
Jetzt können wir von product-binary nutzen und prüfen ob richtig funktioniert.
Erklärung: 101 -> 5 100110 -> 38 5 * 38 -> 190 0 1 0 1 1 1 1 1 0 -> 190
Probleminstanzen und Analyseformen
Die Probleminstanz bilden Eingaben, Ausgaben und die Bedingungen, welche die Ergebnis muss sein. Anders gesagt: Das ist ein Funktion, die der Eingabedatenbestand auf Ausgabedatenbestand umgestalten. Jede Problem können wir auf viele Möglichkeiten auflösen, d.h. es gibt viele Instanzen, damit diese Problem auflösen.
Wichtig ist, damit was Eingaben ist und was ist Instanzen.
Beispiel "Man hat 2 Zahlen $x$ und $y$ und es herausfinden ihre Summe" ist Probleminstanzen. "Berechnen 3+6" ist Instanzen.
Es gibt 3 Analyseformen:
Worst-case-Analyse - die im schlechstesten Fall, d.h. für die ungünstige oder aufwändigste Instanz, erfordliche Laufzeit. Dies entspricht auch dem Maximum aller möglichten Laufzeiten.
Average-case-Analyse - die im mittleren Fall (Durchschnitt, arithmetisches Mittel, Erwartungswert) erfordliche Laufzeit.
Best-case-Analyse - die im günstigsten Fall, d.h. für die aufwandsgünstigste Instanz, erforderliche Laufzeit.
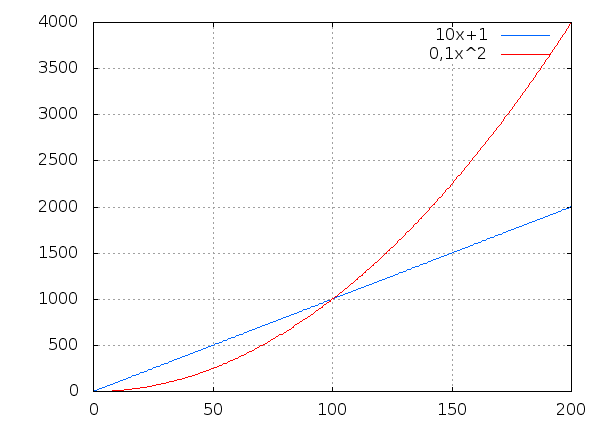
Vergleich von Aufwänden
Die Vergleichungen sind meistens zwischen mindestens 2 Arten Funktionen.
Wichtig ist auch nichtlinearer Gleichungen, die eine Lösung iterativ mit Genauigkeit berechnen.
Beispiel - Türme von Hanoi
Was ist das? Türme von Hanoi ist ein Spiel für Kinder mit folgende Regeln:
- von erste Pfoste auf dritte Pfoste übertragen
- großer Ring kann nicht auf kleiner liegen
- mit eine Bewegung können wir nur Ring aus oben übertragen
Es gibt ein Algorithmus, die die minimale Anzahl der Schritte rechnen.
Funktion mit Iteration: $H_{n} = H_{n-1} + 1 + H_{n} - 1 = 2 * H_{n} + 1 - 1 = 2^{n} - 1$
Funktion mit Rekursion: $H_{n} = 2 * H(n-1) + 1$
Frage: -wenn ein Man für ein Bewegung 1s braucht (Rings/s), -er kann am schnellsten Methode (keine Fehler). Wie viel braucht er Zeit, um die Türme mit 64 Rings zu übertragen?
Antowrt ??
Übungen
1. Türme von Hanoi
- Mithilfe Vorlesung, Internet und selbste Erfahrung schreibst du ein Programm über Türme von Hanoi. Das Programm must zeigt jede Schritt, welche braucht man, damit Spiel gewinnen.
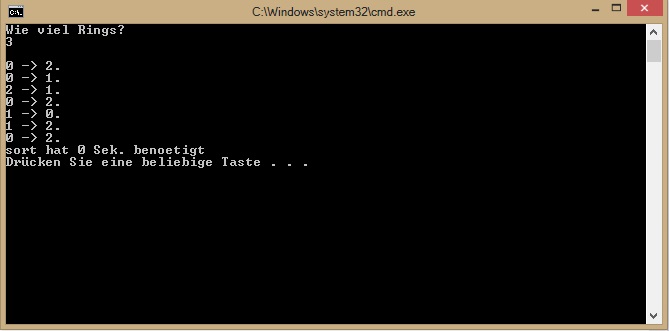
Die Anzahl den Rings sollen wir selbst in Konsole angeben. Mit 3 Rings sollen wir ungefähr diese Bild bekommen.
- Wenn du von Rekursion Funktion genutzt hast, schreibst du jetzt neu-glech Program aber mit Iteration Funktion. Oder natürlich umgekehrt (Erste Iteration - zweite Rekursion Funktion)
- Bis deine zwei Programmen addierst du Zeitmessung und prüft welche Funktion ist schneller.
- Gibt es die Möglichkeit, damit die Rekursion beschleunigen? Wenn ja, machst du das.
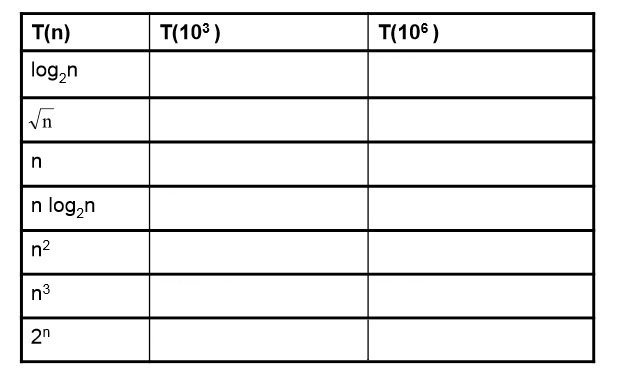
2. Aufwands Tabelle
Bitte ergänzen die Tabellen. In leere Plätze schreibst du die Zeitmessung dem Program.
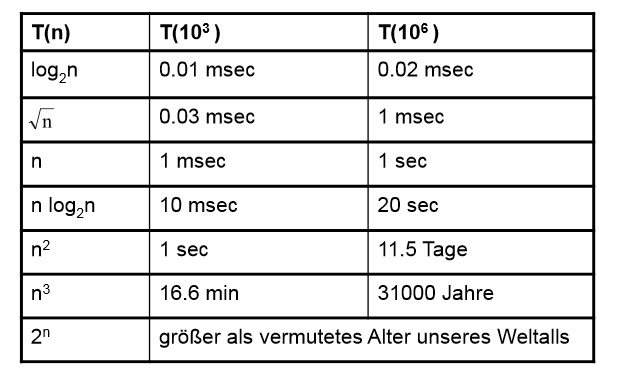
10 minuten vor Ende der Übungen wird die Tabelle mit den Antworten veroffentlicht.