Einführung SS12
Aus ProgrammingWiki

Inhaltsverzeichnis |
Effizienzbegriff
Qualitative Beschreibung von Effizienz
- Ein Algorithmus heißt effizient, wenn er ein vorgegebenes Problem mit möglichst geringem Ressourcenaufwand (Zeit, Speicher) löst.
Diese Beschreibung hält einer quantitativen Bewertung effizienter Algorithmen nicht stand und muss von daher präzisiert werden. Außerdem ist zu beachten, dass Zeit und Speicher ineinander "umwandelbar" sind. D.h., wenn man bei der Modellierung möglichst knappen Speicher wählt, kann es sein, dass dies die Berechnungskomponente des Algorithmus' belastet: Ein Zusatzaufwand kann erforderlich sein, da gewisse Daten zwischengerechnet werden müssen, weil sie nicht direkt zur Verfügung stehen.
Wir werden uns im Folg. im Wesentl. der Zeiteffizienz von Algorithmen widmen.
Problem und Instanzen eines Problems
Es ist bekannt, dass ein betrachtetes Programm für verschiedene Eingaben verschiedene Rechenzeiten zur Bestimmung der entsprechenden Ausgaben benötigt. Wenn wir an einen Primzahltest durch Probeteiler für eine zu untersuchende natürliche Zahl $n$ denken, ist das nicht verwunderlich: Für sehr große Primzahlen ist das wesentlich aufwändiger als für kleine Zahlen, denn es gibt viel mehr Teilerkandidaten.
Häufig ist es außerdem so, dass die Bearbeitungen "vergleichbarer" Eingaben völlig verschiedene Zeitaufwände erfordern. In unserem Primzahltest-Beispiel erfordert die Untersuchung der Zahl $49$ bereits vier Probeteiler, nämlich $2,3,5,7$, während für $50$ schon im ersten Schritt klar ist, dass sie keine Primzahl sein kann, weil sie gerade ist.
Das Beispiel zeigt, dass es falsch wäre zu sagen, dass der Berechnungsaufwand mit zunehmender Problemgröße $n$ steigt. Es gibt vielmehr "solche und solche" Kandidaten nahezu gleicher Größe. Als Größe legen wir die Stelligkeit der gewählten Darstellung, z.B. zweistellige Zahlen im Dezimalsystem, fest.
Deshalb macht es Sinn, die Eingabewerte in Gruppen gleicher Größe einzuteilen. Im Beispiel untersuchen wir also den Aufwand für den Primzahltest für $n$-stellige Zahlen. Für jede Gruppe, z.B. $n=10, 100, 1000, 10000, 100000, 1000000$, wählen wir z.B. $k=5$ Kandidaten zufällig aus und ermitteln die zugehörigen Zeitaufwände. Die folgende Tabelle zeigt den Kern unserer experimentellen Vorgehensweise.
| $n$ | 1 | 2 | 3 | 4 | 5 | $T(n)$ |
|---|---|---|---|---|---|---|
| 10 | ... | ... | ... | ... | ... | .?. |
| 100 | ... | ... | ... | ... | ... | .?. |
| 1000 | ... | ... | ... | ... | ... | .?. |
| 10000 | ... | ... | ... | ... | ... | .?. |
| 100000 | ... | ... | ... | ... | ... | .?. |
| 1000000 | ... | ... | ... | ... | ... | .?. |
Wenn wir uns nun vorstellen, dass die Pünktchen durch die ermittelten Rechenzeiten (z.B. als Takte einer abstrakten Maschine; s. weiter unten) ersetzt wurden, bleibt die Frage nach dem Ersatz des jeweils zugehörigen Fragezeichens.
Je nach Analysetyp macht es Sinn entweder das Maximum, das Minimum bzw. das arithmetische Mittel zu bestimmen:
- worst-case-Analyse: liefert eine (sichere) Aussage zum schlechtestmöglichen Aufwandsverhalten.
$$T(n)=\max_k\{T(i)\mid i\in I_n\}$$
- best-case-Analyse: gibt die bestmögliche Performance-Erwartung (eher unpraktikel).
$$T(n)=\min_k\{T(i)\mid i\in I_n\}$$
- average-case-Analyse: Wenn die Differenz zwischen worst- und best-case-Analyse sehr groß ist, gibt die average-case-Analyse mehr Aufschluss.
$$T(n)=\frac{1}{k}\sum\limits_{i\in I_n}T(i)$$
In obigen Ausdrücken steht $I_n$ für die Menge der Instanzen der Problemgröße $n$ und $k$ bezeichnet die Anzahl der Instanzen der Größe $n$, d.h. $k=|I_n|$.
Für die Bestimmung der jeweiligen Rechenzeit käme prinzipiell natürlich eine Stoppuhr (Handy mit Stopp-App o.ä.) infrage. Diese Methode wäre allerdings sehr fehleranfällig.
Übungsaaufgabe: Begründen Sie diese Aussage.
Deshalb führen wir die Zeitmessung auf die Bestimmung der erforderlichen Arbeitstakte einer abstrakten Maschine zurück -- ganz nach dem Vorbild der atomaren Operationen bei der Karatsuba-Multiplikation zweier natürlicher Zahlen.
Beispiele
Binäre Suche
Gegeben sind eine aufsteigend sortierte Liste $(a_1,a_2,\ldots,a_n)$, mit $a_1<a_2<\ldots <a_n,\; n>0,$ und ein in dieser Liste enthaltenes Element $x=a_k$. Gesucht ist $k$.
Der Algorithmus arbeitet nach dem Prinzip "Teile und herrsche":
- Wähle $m=links+\left\lfloor\frac{rechts-links}{2}\right\rfloor$. D.h. $1\leq m\leq \left\lfloor\frac{n+1}{2}\right\rfloor<n$.
- Falls $x=a_m$, Ausgabe $k=m$. Stopp.
- Falls $x<a_m$, suche weiter in $(a_{links},a_2,\ldots,a_m)$.
- Falls $x>a_m$, suche weiter in $(a_{m+1},a_{m+2},\ldots,a_{rechts})$.
$links$ bzw. $rechts$ steht für den jeweiligen Listen-Index, beginnend mit $1$. Beim Aufruf gilt $links=1$ und $rechts=n$.
Mit dem folgenden Aufruf wird die Suche eines in einer Liste mit 30 Zufallszahlen aus dem Iintervall $[0;50[$ vorhandenen Elements durchgeführt. Die erforderlichen Hilfsprozeduren random und geordneteZufallsliste zur Erzeugung einer sortierten Zufallszahlenliste stehen zur Verfügung. Zu beachten ist, dass die Anzahl der paarweise verschiedenen Zufallszahlen einer Liste nicht größer sein darf als die Größe des Intervalls aus dem sie genommen werden.
Experimentieren Sie ruhig mit $n=3000$ und Zufallszahlen aus $[0;5000[$.
Zur Aufwandsabschätzung nehmen wir vereinfachend an, dass $n$ eine Zweierpotenz ist, also $n=2^d$, mit $d\in\mathbb{N}$. Im worst case sind dann genau $d=\log_2n$ Teilungen der anfangs gegebenen Liste $(a_1,a_2,\ldots,a_n)$ möglich.
Da die Aufwände für die Berechnung von $m$ und die Vergleiche von $x$ mit $a_m$ bei jedem Aufruf der Suchprozedur einen konstanten Wert $c$ haben, kann man den Gesamtaufwand im worst case mit $\mathcal{O}(\log_2n)$ ansetzen.
Die best-case-Analyse führt hingegen zu $\mathcal{O}(1)$: Man denke nur daran, dass das gesuchte $x$ gleich beim ersten Vergleich gefunden wird.
Auf die Untersuchung des average case wollen wir hier verzichten. Hierfür wäre es notwendig, entsprechende Betrachtungen mit Wahrscheinlichkeiten durchzuführen.
Dublettensuche in einer (unsortierten) Liste
Gegeben ist eine unsortierte Liste $(a_1,a_2,\ldots,a_n), n>0,$ natürlicher Zahlen.
Gesucht ist das Element, das mehrfach (mindestens zweimal) in der Liste vorkommt. Ist ein solches Element $a_k$ überhaupt vorhanden, stoppt der Algorithmus mit dessen Ausgabe, andernfalls gibt er nichts aus. Gesucht ist also das kleinste $k, 1\leq k,m\leq n,$ mit $a_k=a_m$ und $k<m$.
Langsames Verfahren
Ein stringentes Verfahren zur Dublettensuche vergleicht jedes Listenelement mit allen Elementen, die diesem in der Liste folgen, also $a_i$ wird verglichen mit $a_{i+1},a_{i+2},\ldots,a_{n}$. Für $i=1,2,\dots,n-1$ sind das $n-1, n-2,\ldots,1=\sum\limits_{j=1}^{n-1}j=\frac{n(n-1)}{2}$ Vergleiche jeweils konstanten Aufwands. Damit ist klar, dass der Gesamtaufwand im worst case in $\mathcal{O}(n^2)$ liegt.
Wir wollen das experimentell untermauern.
Die folgende Prozedur stellt eine Liste mit $n=30$ Zufallszahlen aus dem Intervall $[0,m[$ bereit, $m=100$.
Die Dublettensuche wird durch zwei verschachtelte Laufanweisungen (do-Schleifen) realisiert. Die darin enthaltene Variable escape sorgt dafür, dass der Zyklus verlassen wird, sobald eine Dublette gefunden wurde. Außerdem wird die Zahl der Vergleiche ausgegeben.
Der worst case ist gegeben, wenn die Zufallsliste keine Dublette enthält. Für $n=20$ ergeben sich dann $\frac{20\cdot 19}{2}=190$ Vergleiche.
Übungsaufgabe: Führen Sie eine empirische average-case-Analyse durch und vergleichen Sie Ihr Ergebnis mit dem Ergebnis der worst-case-Analyse.
Schnelles Verfahren
Eine aus dem Hashing bekannte Idee liefert ein wesentlich schnelleres Dublettsuchverfahren. Es braucht allerdings auch viel mehr Speicher. Das ist keine Seltenheit: Gibt man mehr Speicher, kann der darüber arbeitende Prozess Rechenzeit einsparen. Umgekehrt haben Speichersparmaßnahmen mitunter negative Auswirkungen auf die Performance.
Die Idee besteht darin, für jedes Element $A[i]$ des Zufallsvektors in einem zweiten Vektor $B[A[i]]$ dessen Existenz zu vermerken. Der Wert des Elements ist also der betreffende Index von $B$. Vektor $B$ wird mit false initialisiert, was so viel bedeutet, wie dass das betrachtete Element beim Durchlaufen des Vektors (mit aufsteigendem Index) noch nicht vorkam. Für jedes Element wird true in $B[A[i]]$ vermerkt, wenn der vorherige Wert false war. Ist der ursprüngliche Wert jedoch true, so ist klar, dass der betrachtete Wert (als Listenelement) bereits vorhanden ist, d.h. eine Dublette wurde gefunden.
Wenn wir also Zufallszahlen aus $[0,m[$ zulassen, liegt der Index von Vektor $B$ zwischen $0$ und dem Maximum aller Werte aus $A$, wobei $\max(a_i)<m$. Da die Bestimmung dieses Maximums bereits bei der Zufallslistenbildung erledigt werden kann, wird der dafür erforderliche (einmale) Aufwand nicht veranschlagt. Verwendet man (etwas verschwenderisch) einfach $m$, entfällt er gänzlich.
Wie wir sehen können, finden maximal $n-1$, bei $n=20$ also $19$, Vergleiche statt. Das Verfahren arbeitet im worst case mit linearem Aufwand: $\mathcal{O}(n)$.
Polynomialer vs. exponentieller Aufwand
Polynomialer Aufwand
$$T(n)=a_r n^r + a_{r-1} n^{r-1} + \ldots + a_1 n^1 + a_0 = \sum\limits_{i=0}^ra_i,\text{ mit } r\in\mathbb{N}_0,~a_r,\ldots, a_0\in\mathbb{R}_0^+,~a_r\neq 0.$$
Hierzu zählen auch die Aufwandsfunktionen, die sich mit Logarithmen der folgenden Form $T(n)=a\cdot\log_c n$ beschreiben lassen. Man spricht von quasipolynomialen Aufwänden.
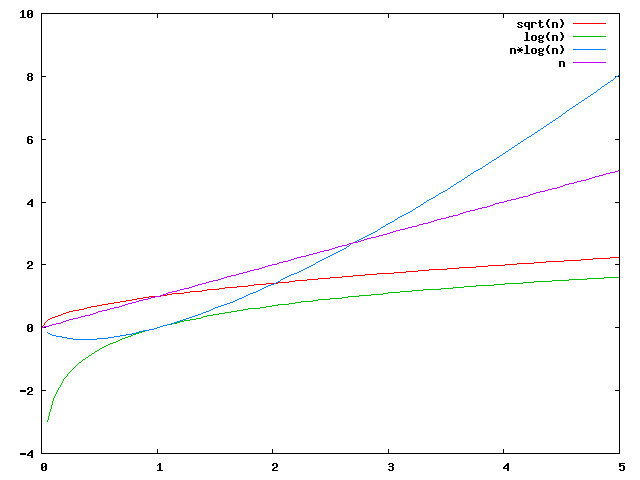
Die grafische Darstellung dieser Funktionen macht das jeweilige Aufwandswachstum im Vergleich gut deutlich, ist aber für die Praxis -- also für sehr große Werte der betrachteten Problemgröße -- eher uninteressant. Da gilt nämlich, dass polynomiale Aufwände geradezu harmlos sind im Vergleich zu exponentiellen.
Exponentieller Aufwand
$$T(n)=c\cdot z^n, \text{ wobei }z,~c\in\mathbb{R}_0^+,~z>1.$$
Auch die Fakultätsfunktion beschreibt einen exponentiellen Zusammenhang, wie die Stirlingsche Formel zeigt: $$n!\approx \sqrt{2\pi n}\left(\frac{n}{e}\right)^n.$$
Aufgrund des gegebenen Definitionsbereiches bestehen die Graphen der Funktionen eigentlich aus Punkten. Zur besseren Visualisierung werden sie jedoch als geschlossene Linienzüge dargestellt.
Asymptotische Aufwandsordnungen
Kleine Zeitaufwände zu vergleichen ist nicht sinnvoll. Schon Computer geringer Leistungsfähigkeit rechnen in diesem Bereich sehr schnell. Dem gegenüber kann es für große und sehr große Werte für $n$ dazu kommen, dass auch sehr leistungsstarke Prozessoren unakzeptable Rechenzeiten beanspruchen.
Bei der Beurteilung des Aufwandsverhaltens ist deshalb im Allg. nicht von Interesse, welche Koeffizienten in dem konkreten Funktionsausdruck für $T$ vorkommen. Dies führt zur asymptotischen Analyse.
Insbesondere haben zwei Funktionen $f,t:\mathbb{N}\mapsto\mathbb{R}_0^+$ die gleiche Wachstumsrate, wenn es zwei positive reelle Konstanten $c$ und $d$ gibt, so dass für alle hinreichend großen $n$ gilt $c\leq\frac{f(n)}{t(n)}\leq d$. $f$ wächst schneller als $t$, wenn für alle positiven reellen Konstanten $c$ gilt $f(n)\geq c\cdot t(n)$.
Für die mathematische Beschreibung dieses Sachverhalts wird die "Groß-O"-Notation verwendet. Die Sprechweise von $\mathcal{O}(f)$ ist "Groß-O von f". Mit dem $\mathcal{O}$-Kalkül werden wir uns am meisten beschäftigen. \begin{eqnarray*} \mathcal{O}(f) &=& \{t:\mathbb{N}\mapsto\mathbb{R}_0^+\mid \exists c\in\mathbb{R}^+\ \exists n_0\in\mathbb{N}\ \forall n\geq n_0:\ t(n)\leq c\cdot f(n)\} \\ \Omega(f) &=& \{t:\mathbb{N}\mapsto\mathbb{R}_0^+\mid \exists c\in\mathbb{R}^+\ \exists n_0\in\mathbb{N}\ \forall n\geq n_0:\ t(n)\geq c\cdot f(n)\} \\ \Theta(f) &=& \mathcal{O}(f)\cap \Omega(f) \end{eqnarray*}
Beispielsweise hat die Karatsuba-Multiplikation zur Multiplikation zweier $n$-stelliger natürlicher Zahlen einen Aufwand in $\mathcal{O}(n^{1.58})$ und die Schulbuchmethode in $\mathcal{O}(n^{2})$.
Man sollte sich klar machen, dass $\mathcal{O}(f)$ eine Menge von Funktionen ist, s. Definition weiter oben. Offensichtlich gilt für einen polynomialen Aufwand der Form $$T(n)=\sum\limits_{i=0}^k a_i\cdot n^i,\text{ mit } a_k>0$$ $T\in\Theta(n^k)$, d.h. $T\in\mathcal{O}(n^k)$ und $T\in\Omega(n^k)$, denn $T(n)\leq \underbrace{\sum\limits_{i=0}^k a_i}_{c}\; \cdot\; \underbrace{n^k}_{f(n)}$.
Hiernach gilt (wiederum in gängiger Kurzschreibweise) $3n^2+8n=\mathcal{O}(n^2)$. Der Grad des Polynoms regiert die Aufwandsordnung.
Bei einer etwas gröberen (nicht zu empfehlenden aber möglichen) Abschätzung nach oben wäre allerdings auch $3n^2+8n=\mathcal{O}(n^3)$ richtig. Folglich könnte man schreiben: $$3n^2+8n=\mathcal{O}(n^2)=\mathcal{O}(n^3).$$ Obwohl es sich formal um eine Gleichheit handelt, gilt diese Beziehung nur von links nach rechts gelesen. Das ist sehr wichtig und außergewöhnlich, aber z.B. für $g(n)=4n^3$ gelten nun mal $g\in\mathcal{O}(n^3)$ und $g\not\in\mathcal{O}(n^2)$.
Übungsaufgaben:
- Bearbeiten Sie die Aufgaben 2.6-2.9 auf S. 35 (CW: AuK).
- Mitunter ist es notwendig, mit asymptotischen Aufwänden zu rechnen. Dann gelten bestimmte Rechenregeln, etwa wie in Satz 2.1 (S. 35). Führen Sie den zugehörigen Beweis (Aufg. 2.5).
Großer Bedarf an mathematischen Hilfsmitteln
Approximation von Funktionen
Experimentelle (empirische) Aufwandsanalysen führen zu konkreten Wertepaaren. Stellt man sie grafisch dar, ergibt sich eine "Buckelkurve". Die gesuchte Aufwandsfunktion ist die, die sich möglichst gut in diese Punktewolke einfügt, sie bestmöglich annähert oder approximiert.
Je nach Vermutung versucht man also die Kooeffizienten entweder eines polynomialen oder eines exponentiellen Terms zu finden. Hierfür gibt es interessante mathematische Werkzeuge. Außerdem steht ein Maxima-Worksheet zur Verfügung.
Lösung rekurrenter Gleichungen
Sog. rekurrente Gleichungen entstehen, wenn man das Aufwandsverhalten eines Programms anhand seiner Struktur beschreibt. Dies gelingt -- insbesondere bei rekursiven Prozeduren -- oftmal leichter als die Angabe einer expliziten Funktion für $T$.
Beispielsweise haben wir für die weiter oben betrachtete Binäre Suche den Aufwand rasch angeben können, weil die Zahl der Aufrufe infolge der fortgesetzten Teilung der vorgegebenen Liste durch $\log_2n$ beschränkt werden konnte.
Oft ist das nicht so offensichtlich. Auch im Falle der binären Suche hätten wir eine Aufwandsbeziehung, wie etwa die folgende, aus dem Verfahren direkt ablesen können: $$\begin{eqnarray*} T(1) &=& a \\ T(n) &=& b + T\left(\frac{n}{2}\right),~n>0 \end{eqnarray*}$$
$a$ und $b$ stehen für (positive) konstante Aufwände.
Man braucht nun Methoden, um aus diesen Beziehungen eine explizite Funktion der oben beschriebenen Art, also (pseudo)polynomial oder exponentiell, zu gewinnen. Im Beispiel erwarten wir soetwas wie $\mathcal{O}(\log_2n)$.
Die wichtigsten Techniken sind:
- Verwendung von CAS
- Raten und Einsetzen
- Iterationsmethode
- Meistermethode
Übungsaufgabe: Machen Sie sich mit diesen Methoden vertraut und bearbeiten Sie die zugehörigen Beispiel. Schließen Sie dabei auch die Schulbuchmethode und das Verfahren nach Karatsuba zur Multiplikation zweier $n$-stelliger natürlicher Zahlen ein.