Effizienz von Algorithmen SS09
Aus ProgrammingWiki

Inhaltsverzeichnis |
Effizienzbegriff
- Ein Algorithmus heißt effizient, wenn er ein vorgegebenes Problem mit möglichst geringem Ressourcenaufwand (Zeit, Speicher) löst.
Diese Formulierung muss weiter präzisiert werden. Außerdem ist zu beachten, dass Zeit und Speicher ineinander "umwandelbar" sind, d.h. wenn man bei der Modellierung knappen Speicher wählt, kann es sein, dass der Algorithmus Zusatzaufwand betreiben muss, da gewisse Daten zwischengerechnet werden müssen und eben nicht direkt zur Verfügung stehen.
Beispiel: Dublettensuche in einer Liste
Vereinfachend nehmen wir an, dass es sich um Listen mit Zufallszahlen handelt. Sobald ein doppeltes Listenelement gefunden wurde, soll das Verfahren mit der Ausgabe dieses Elements stoppen, anderenfalls stoppt der Algorithmus ohne Ausgabe eines Wertes.
Das Programm aus dem ersten Lösungsvorschlag arbeitet mit quadratischem Aufwand:
Die folgende Prozedur stellt eine Liste mit Zufallszahlen aus dem Intervall
bereit,
.
Die Dublettensuche wird durch zwei verschachtelte Laufanweisungen berechnet. Die darin enthaltene Variable escape sorgt dafür, dass der Zyklus verlassen wird, sobald eine Dublette gefunden wurde.
Die Anzahl der Vergleiche beträgt höchstens . Für
sind das also höchstens 190 Vergleiche. Die Dublettenermittlung erfolgt also mit quadratischem Aufwand.
Eine aus dem Hashing bekannte Idee liefert ein wesentlich schnelleres Dublettsuchverfahren. Es braucht allerdings auch viel mehr Speicher. Das ist keine Seltenheit: Gibt man mehr Speicher, kann der darüber organisierte Prozess Rechenzeit einsparen. Umgekehrt haben Speichersparmaßnahmen negative Auswirkungen auf die Performance.
Die Idee besteht darin, für jedes Element des Zufallsvektors in einem zweiten Vektor
dessen Existenz zu vermerken. Der Wert des Elements ist also der betreffende Index von
. Vektor
wird mit
initialisiert, was so viel bedeutet, wie das das betrachtete Element beim Durchlaufen des Vektors noch nicht vorkam. Für jedes Element wird
in
vermerkt, wenn der vorherige Wert
war. Ist der ursprüngliche Wert jedoch
, so ist klar, dass der betrachtete Wert schon vorhanden ist, d.h. eine Dublette wurde gefunden.
Die Bestimmung des Maximums der in der Liste zusammengefassten Zufallszahlen kann bei der Listenbildung erledigt werden und wird deshalb aufwandsmäßig nicht zusätzlich veranschlagt.
Es finden maximal , bei
also
Vergleiche statt.
Polynomialer vs. exponentieller Aufwand
Polynomialer Aufwand:
,
Hierzu zählen auch die Aufwandsfunktionen, die sich mit Logarithmen der folgenden Form beschreiben lassen. Man spricht von quasipolynomialen Aufwänden.
Exponentieller Aufwand:
, wobei
.
Auch die Fakultätsfunktion beschreibt einen exponentiellen Zusammenhang, wie die Stirlingsche Formel zeigt:
.
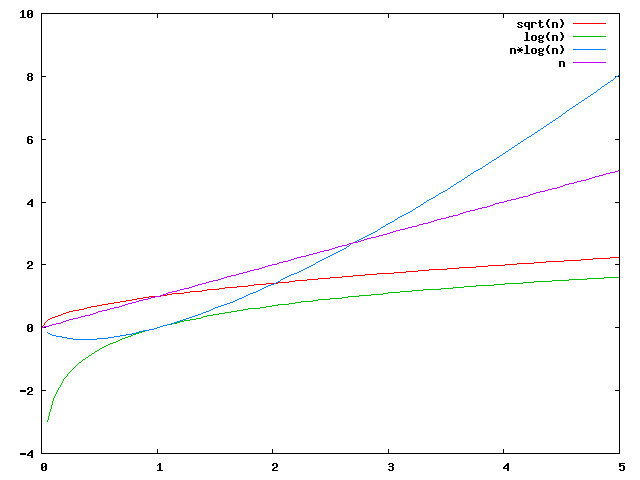
Aufgrund des gegebenen Definitionsbereiches bestehen die Graphen der Funktionen eigentlich aus Punkten. Zur besseren Visualisierung werden sie jedoch als geschlossene Linienzüge dargestellt.
Vergleich verschiedener polynomialer und pseudopolynomialer Aufwände