Dynamisches Programmieren WS13-14

Aus ProgrammingWiki

< AuK
Wechseln zu: Navigation, Suche

Loading
Autoren

Jens Klinger

Daniel Franke


Inhaltsverzeichnis

Einführung

Das Prinzip "Teile und Herrsche" dient als Grundlage für viele Algorithmen: Um ein umfangreiches Problem zu lösen, zerlegt man es in kleinere Teilprobleme, die unabhängig voneinander gelöst werden können. In der dynamischen Programmierung wird dieses Prinzip aufgegriffen und weiterentwickelt. Im Gegensatz dazu wird das Bottom-up-Verfahren angewendet. D.h. dynamische Programmierung führt dann zu einer Lösung, wenn das Optimierungsproblem aus vielen gleichartigen Teilproblemen besteht und sich eine optimale Gesamtlösung des Problems aus optimalen Teillösungen zusammensetzt. Zu diesem Zweck werden alle Teilprobleme "von-unten-her" berechnet und in eine Tabelle eingetragen, um eine erneute Berechnung zu vermeiden.

Die Entwicklung eines dynamischen Programms kann in vier Schritte unterteilt werden:

  1. Charakterisierung der Struktur eines Programms.
  2. Definieren des Wertes einer optimalen Lösung rekursiv.
  3. Berechnung des Wertes einer optimalen Lösung durch den bottom-up-Ansatz.
  4. Konstruktion einer zugehörigen, optimalen Lösung aus den schon berechneten Daten.

Bei der Anwendung der dynamischen Programmierung können immer folgende Schwierigkeiten auftreten:

  • Es ist nicht immer möglich, die Lösungen kleinerer Probleme so zu kombinieren, dass sich die optimale Lösung eines größeren Problems ergibt.
  • Die Anzahl der zu lösenden Teilprobleme kann unvertretbar groß werden.
  • Die Zerlegung in unabhängige und überlappungsfreie Teilprobleme ist häufig nicht möglich.

Es gibt daher viele Probleme, für die die dynamische Programmierung nicht anwendbar bzw. ineffizienter ist als Standardalgorithmen. In diesem Wiki werden daher einige Probleme vorgestellt, für die dynamische Programmierung sehr effizient ist.

Doch zunächst soll auf grundlegende Schwierigkeiten bei der dynamischen Programmierung hingewiesen werden.

Rekursiver Lösungsansatz = rekursiver Algorithmus?

In diesem Beispiel soll anhand der Berechnung der Fibonacci-Folge gezeigt werden, warum in der dynamischen Programmierung zumeist iterative Lösungsmethoden mit Bottom-up-Ansatz verwendet werden.

Zur Erinnerung, die Fibonacci-Folge ist eine unendliche Folge von Zahlen, bei der die Summe der beiden Vorgänger die unmittelbar folgende Zahl ergibt.

Rekursive Definition

$f(0) = 1$

$f(1) = 1$

$f(n) = f(n-1)+f(n-2), \text{mit n} \geq 2$

Rekursive Lösung

Abschätzung der Laufzeit

Die Funktion zur Berechnung der Fibonacci-Zahlen wächst exponentiell: $f(n) = \frac{1}{\sqrt{5}}[(\frac{1+\sqrt5}{2})^n - (\frac{1-\sqrt5}{2})^n] \approx \frac{1}{\sqrt{5}}(1,618...)^n$

Wir müssen beachten, dass wir mit einer rekursiv definierten Funktion, auch für die Abschätzung der Laufzeit, eine Rekursionsgleichung erhalten!

Am Beispiel:

$T(n) = \text{Anzahl der Schritte zur Berechnung von } fib(n)$

$T(0) = 1$

$T(1) = 1$

$T(n) = T(n-1)+T(n-2)$

Wir sehen, dass die Formel zur Abschätzung der Laufzeit identisch mit der Formel zur Berechnung der Fibonacci-Zahl ist. Daraus können wir wiederum schlussfolgern, dass es sich um einen exponentiellen Aufwand $\mathcal O(2n)$handelt.

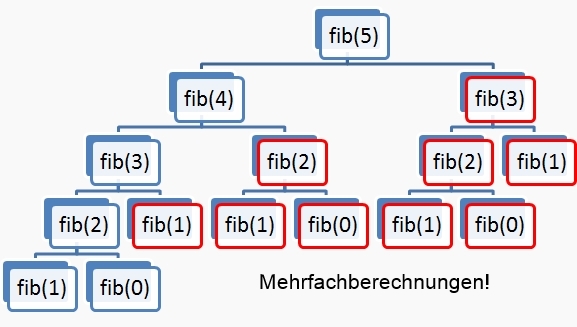
Baumdarstellung


Alternativen

Aufgrund dieser Schwierigkeiten wird in der dynamischen Programmierung traditionell der iterative Lösungsansatz bevorzugt. Doch auch dieser hat Nachteile. Wie bereits erwähnt, müssen alle Teillösungen berechnet werden, auch diese, die nicht zur optimalen Lösung des Problems beitragen. Der größte Nachteil besteht jedoch darin, dass der rekursiv gebildete Top-down-Ansatz in einen iterativen Bottom-up-Algorithmus umgewandelt werden muss, was sehr aufwendig ist und sich dabei schnell Fehler einschleichen.

Doch auch dieses Problem lässt sich lösen. Eine Variante der dynamischen Programmierung, die oft so effizient wie die traditionelle Methode ist, heißt Memoisation (eng. memoizing). Im nächsten Abschnitt wird am 0/1 Rucksackproblem gezeigt, wie iterative und rekursive Lösungsansätze aussehen können.

Lösung des 0/1 Rucksackproblems

Beim Rucksackproblem handelt es sich um ein Optimierungsproblem der Kombinatorik. Aus einer bestimmten Menge von Objekten, die jeweils ein Gewicht und einen Wert haben, soll eine Teilmenge ausgewählt werden, deren Gesamtgewicht ein vorgegebenes Gewichtslimit nicht überschreitet. Hierbei gilt die Optimalitätsbedingung, denn die optimale Gesamtlösung lässt sich aus optimalen Teilproblemen zusammensetzen. Bezogen auf das Rucksackproblem bedeutet das, Gegenstand i wird in den optimal gefüllten, auch leeren, Rucksack gelegt. D.h. alle zur Auswahl stehenden Gegenstände können solange in den Rucksack gelegt werden, solange sie noch Platz haben.

Für den optimal gefüllten Rucksack gilt die rekursive Definition mit:


$i=\text{ Gegenstand }$

$g=\text{ Gewicht }$

$w=\text{ Wert des Gegenstands }$

$n = \text { Anzahl der Gegenstände }$

$K = \text{ Kapazität des Rucksacks }$

$wert(i,g) = \text{ Optimaler Wert für die Gegenstände }$

$wert(n,K)=\text{ Optimaler Gesamtwert }$


$wert(i,g) = \begin{cases} 0, & wenn \ i =0 \\ wert(i-1, g), & wenn \ i > 0 \ und \ g-g_{i} < 0\\ max(wert(i-1,g), wert(i-1, g-g_{i})+w_{i}), & sonst \\ \end{cases}$


Der Fall $wert(i,g) = wert(i-1,g)$ bezieht sich auf einen Gegenstand, der die Restkapazität des Rucksacks überschreiten würde. D.h. $wert(i-1,g)$ ist der Maximalwert aus $1,2,...,i-1$ Gegenständen mit Bezug auf die Kapazität des Rucksacks. Der letzte Fall $wert(i,g) = max(wert(i-1,g), wert(i-1, g-g_{i})+w_{i})$ beschreibt die Maximierung des Wertes in Berücksichtigung des Gewichtes.


Iterativer Algorithmus

Der iterative Lösungsansatz lässt sich, wie bereits erwähnt, nicht mit einer rekursiven Vorschrift umsetzen. Jedoch ist es möglich, die Überlegungen aus dieser Vorschrift zu verwenden und in einen iterativen Lösungsansatz umzuwandeln.

Das soll am folgenden Beispiel demonstriert werden:

$i$ 1 2 3 4 5
$g_i$ 2 2 6 5 4
$w_i$ 6 3 5 4 6

Zur Lösung wird die Gegenstandsliste mit der Prozedur $gegenstaende$ (Quelle: [1], S. 102) auf Vektoren als Gewicht/Wert-Paar abgebildet. Auf das jeweilige Gewicht bzw. den jeweiligen Wert kann dann mittels der Prozeduren $gewicht$ und $wert$ zugegriffen werden. Die Prozedur $gesamtwert-iterativ$ füllt dann eine Tabelle mit den jeweils maximalen Gesamtwerten für die aktuell betrachteten Gegenstände (Zeile) und das darauf bezogene Gesamtgewicht (Spalte). Das Problem hierbei ist die Speicherung aller Werte in der Tabelle, was eine sehr hohe Speicherbelastung nach sich zieht. Für den hier dargestellten Fall genügt es jedoch, wie in der rekursiven Vorschrift notiert, die jeweils letzten beiden Zeilen (zeileAlt und zeileNeu) zu speichern. D.h. die $i$-te Zeile wird aus der $i-1$-ten Zeile berechnet.

Der Aufruf von (gesamtwert-iterativ 5 10) erzeugt folgende Tabelle:

$n/K$ $0$ $1$ $2$ $3$ $4$ $5$ $6$ $7$ $8$ $9$ $10$
$0$ 0 0 0 0 0 0 0 0 0 0 0
$1:(g_i=2; w_i=6)$ 0 0 6 6 6 6 6 6 6 6 6
$2:(g_i=2; w_i=3)$ 0 0 6 6 9 9 9 9 9 9 9
$3:(g_i=6; w_i=5)$ 0 0 6 6 9 9 9 9 11 11 14
$4:(g_i=5; w_i=4)$ 0 0 6 6 9 9 9 10 11 13 14
$5:(g_i=4; w_i=6)$ 0 0 6 6 9 9 12 12 15 15 15

Aufwandsbetrachtung

An der iterativen Prozedur kann man sehr gut erkennen, dass sich der Aufwand aus der Berechnung der Tabelle mit allen Spalten und Zeilen ergibt.

$\mathcal O(n\cdot K)\cdot\mathcal O(1)=\mathcal O(nK)$

Nimmt man nun an, dass $K$ eine Konstante ist, ergibt sich ein linearer Aufwand $\mathcal O(n)$. Doch da für alle $n$ Gegenstände gilt, dass $g_i \le K$ ist, lässt sich ein Zusammenhang zwischen $n$ und $K$ herstellen. Ein solcher Algorithmus heißt pseudopolynomiell und es muss die Eingabelänge der Werte einer beliebigen Instanz des 0/1 Rucksackproblems untersucht werden. Dazu müssen die Eingabewerte in Binärdarstellung umgewandelt und eine obere Schranke festlegt werden. Wir legen sozusagen die Eingabewerte auf das Band einer Turing-Maschine. Für das 0/1 Rucksackproblem besteht die Eingabe aus $2n+1$ natürlichen Zahlen, also dem Gewicht ($g_1,g_2,...,g_n$), dem Wert ($w_1,w_2,...,w_n$), und der Gesamtkapazität $K$. Zusätzlich definieren wir einen Maximalwert $\hat w = max\{w_1,w_2,...,w_n\}$.

Die Beschränkung der Eingabelänge muss folgendermaßen aussehen:

$\mathcal O(n\cdot(log_2 K+log_2 \hat w)+log_2 K)$ = $\mathcal O(n\cdot(log_2 K+log_2 \hat w))$.

Um nun die Rechenzeit des Algorithmus zu bestimmen, müssen wir eine Länge für $K$ festlegen, z.B. $K=2^n$ und damit $\hat w \le 2^n$. Daraus folgt, dass die Rechenzeit bei $\mathcal O(n^2)$ liegt und der Algorithmus eine exponentielle Rechenzeit $\mathcal O(n\cdot 2^n)$ hat.

In diesem Fall lässt sich die polynomiale Rechenzeit nur erreichen, wenn $K$ durch ein Polynom beschränkt wird. So z.B. $K \le n^{10}$, was zu einer Rechenzeit von $\mathcal O(n^{11})$ führt. Eine solche Beschränkung ist jedoch unüblich, da die Größe und nicht die Bitlänge von $K$ in die Laufzeit eingeht.

Rekursiver Algorithmus

Die Lösung des 0/1 Rucksackproblems mittels Rekursion wird im Folgenden mit einer Prozedur gezeigt, die im ersten Teil ohne memoizing und im zweiten Teil mit memoizing arbeitet.


Ohne Memoizing

Als erstes wird die Prozedur (Quelle: [1], S. 106) ohne memoizing implementiert. Die rekursive Definition kann leicht in die Prozedur überführt werden:

Durch die rekursiven Aurufe wird auch die Menge der zu lösenden Teilprobleme bestimmt. Deshalb kommt es in der Prozedur zu Mehrfachberechnungen. Um dies zu verhindern, wird das sogenannte memoizing eingesetzt. Bei dieser Technik wird vor der Berechnung eines neuen Wertes in der Tabelle nachgeschaut, ob dieser Wert bereits vorhanden ist. Wenn er vorhanden ist, wird er verwendet. Ist er nicht vorhanden, wird er berechnet und zur weiteren Verarbeitung in die Tabelle übernommen. Das wird am folgenden Beispiel gezeigt:

Mit Memoizing

Um die rekursive Prozedur (Quelle: [1], S. 107) mit memoizing zu implementieren, benötigt es nur wenige Änderungen im bereits vorhandenen Quellcode.

Als Résumé bleibt festzuhalten, dass die Ergebnisse mit denen der iterativen Prozedur übereinstimmen. Die rekursive Berechnung ohne memoizing ist selbstverständlich nicht tauglich, da durch die unnötige Mehrfachberechnung die Zahl der rekursiven Aufrufe viel zu hoch ist. Der memoizing- Methode wiederum sollte man den Vorzug vor der iterativen Methode geben, denn sie ist mindestens so schnell wie diese, ermöglicht eine direkte Ableitung der rekursiven Regeln und vermeidet die fehleranfällige Transformation in einen iterativen Bottom-up-Algorithmus.

Needleman-Wunsch-Algorithmus

DNA-Molekül 1 unterscheidet sich von
DNA-Molekül 2 in einem einzigen Basenpaar

Einleitung

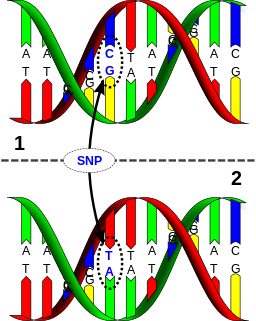
Algorithmen der Bioinformatik sind ein Grund, weshalb die Entschlüsselung der DNA rasante Fortschritte macht. DNA ist eine lineare Verbindung aus Kettenmolekülen, die aus einzelnen chemischen Bausteinen aufgebaut sind. Diese Bausteine sind sogenannte Nukleotide, Moleküle die aus einem Phosphat, einem Zucker und einer Base bestehen, wobei Zucker und Phosphat das Gerüst bilden. Es gibt vier verschiedene Basen, aus denen die DNA aller Lebewesen (auf der Erde) besteht: Adenin, Guanin, Cytosin und Thymin - abgekürzt A, G, C und T. Die Reihenfolge der Anordnung dieser Basen verschlüsselt die Erbinformationen. Um wiederum diese Erbinformationen zu entschlüsseln, benötigen wir die Sequenzanalyse, welche zwei Sequenzen vergleicht und Ähnlichkeiten bewertet.

Zur Analyse werden sog. Stringalgorithmen verwendet. Man kann damit entweder nach exakten Übereinstimmungen suchen, oder nach allen ungefähren Entsprechungen innerhalb einer bestimmten Distanz. Diese Editierung zweier Strings wird Alignment genannt. Die bekanntesten unter diesen Alignment-Algorithmen sind der Smith-Waterman-Algorithmus, der BLAST-Algorithmus und der Needleman-Wunsch-Algorithmus, welcher in diesem Abschnitt vorgestellt wird.

Problemstellung

Der Needleman-Wunsch-Algorithmus berechnet das optimale globale Alignment von zwei Sequenzen. Er erstellt dabei eine Score zur Bewertung der Ähnlichkeit. Je größer die Score, umso größer die Ähnlichkeit. Das Alignment ist eine Folge von Editieroperationen, um die erste Sequenz in die zweite Sequenz zu überführen. Das soll an einem Beispiel gezeigt werden:

Gegeben sind zwei Proteinsequenzen, z.B. die Sequenzen ACGTC und AGTC. Gesucht wird nach der Ähnlichkeit. Werden diese Sequenzen untereinander geschrieben, ist keine Übereinstimmung zu erkennen.


A C G T C
A G T C


Durch Einfügen von Gaps werden nun Übereinstimmungen in Teilstücken erreicht:


A C G T C
A _ G T C


Der Abschnitt GTC bildet dabei die längste gemeinsame Teilsequenz, das Alignment. Die Länge der längsten Teilsequenz ist ein Maß für die Ähnlichkeit der Sequenzen. Die Anzahl der Nichtübereinstimmungen des Vergleichs wird als Editier-Distanz bezeichnet. Dieses Maß gibt an, wie viele Buchstabenänderungen, Einfügungen und Löschungen mindestens erforderlich sind, um eine Sequenz in die andere zu überführen. Im obigen Beispiel etwa lässt sich AGTC in ACGTC überführen, indem ein gap zwischen A und G eingefügt wird. Die Editierdistanz beträgt somit 1.

Noch genauer lässt sich die Ähnlichkeit bewerten, wenn die Übereinstimmung gewisser Buchstaben höher bewertet wird als die anderer. Ebenso wenn Nichtübereinstimmungen bestimmter Kombinationen anders bewertet werden und wenn Einfügen und Löschen eine eigene Bewertung bekommen. Im Beispiel wird jede Übereinstimmung mit 3, jede Nichtübereinstimmung mit 0 und jede Einfügung bzw. Löschung mit -1 bewertet. Dazu werden die Variablen $match$, $mismatch$ und $gappenalty$ eingeführt.


$match = 3$

$mismatch = 0$

$gappenalty = -1$


Lösung

Mit dem Needleman-Wunsch-Algorithmus wird erst das Maß der Ähnlichkeit und anschließend ein Alignment berechnet. Gegeben sind zwei Sequenzen $x$ und $y$. Die Längen der Sequenzen werden mit $m\times$$n$ bezeichnet. Bei der Berechnung wird die Funktion $equal$ benutzt, die $i$ und $y$ miteinander vergleicht. Der Funktionswert $equal(i,j)$ ist gleich $match$, wenn das $i$-te Zeichen von $x$ mit dem $j$-ten Zeichen von $y$ übereinstimmt, andernfalls gleich $mismatch$:


$equal(i,j)=\begin{cases} match, & falls \ x_{i}=y_{j}\\ mismatch, & sonst.\\ \end{cases}$



$\text{für alle i in {0, ..., m-1 }, j in {0, ..., n-1}}$


Es wird nun eine $m\times$$n$-Matrix $a$ nach folgender Vorschrift ausgefüllt:


$a_{0, 0} = 0$

${0, j} = a_{0, j-1}+gappenalty$

${i, 0} = a_{i-1, 0}+gappenalty$

${i, j} = max(a_{i-1, j}+gappenalty, a_{i, j-1}+gappenalty, a_{i-1, j-1}+gappenalty)$


$\text{für alle i in {1, ..., m-1}, j in {1, ..., n-1}}$

Im Folgenden der Algorithmus zur Lösung des Beispiels in Java:


Für das Beispiel ergibt sich folgende Matrix:

$ A C G T C
$ 0 -1 -2 -3 -4 -5
A -1 3 2 1 0 -1
G -2 2 3 5 4 3
T -3 1 2 4 8 7
C -4 0 4 3 7 11
  • Die Zahl in der rechten unteren Ecke ist das Maß für die Ähnlichkeit der beiden Sequenzen.
  • Das Alignment lässt sich konstruieren, indem man ausgehend vom rechten unteren Feld in die Richtung geht, aus der das Maximum kommt. Diese Felder sind in der Tabelle fett gekennzeichnet.
  • Wird nach oben gegangen, entspricht das einer Einfügung in die Sequenz $x$.
  • Wird nach links gegangen, entspricht das einer Einfügung in der Sequenz $y$.
  • Wird diagonal nach links oben gegangen, entspricht das einer Übereinstimmung, wenn der Wert des aktuellen Feldes und der Wert des linken oberen Nachbarfeldes sich um $match$ unterscheiden, ansonsten einer Nichtübereinstimmung.

So kommt das folgende Alignment zustande:

$x:$  A C G T C
$y:$  A _ G T C

Aufwandsbetrachtung

Zur Ermittlung der Laufzeit müssen $m\cdot n$ Elemente der Tabelle berechnet werden. Weiterhin muss für jedes Element das Maximum über $\mathcal O(n)+ \mathcal O(m)$ Elemente ermittelt werden. Das ergibt eine Laufzeit von $\mathcal O(max(n,m)^3)$. Die Laufzeit des hier gezeigten Algorithmus beträgt jedoch $\mathcal O(n^2)$, da einheitliche Gap- Kosten verwendet werden und somit bei Editier- Operationen nur die drei benachbarten Zellen beachtet werden müssen. Der Speicherbedarf liegt logischerweise bei $\mathcal O(nm)$.

Übungen

Übungen.pdf (0.5 MB)

Literatur

Von „https://programmingwiki.de/AuK/Dynamisches_Programmieren_WS13-14“
Persönliche Werkzeuge