Durchläufe durch Graphen SS12
Aus ProgrammingWiki

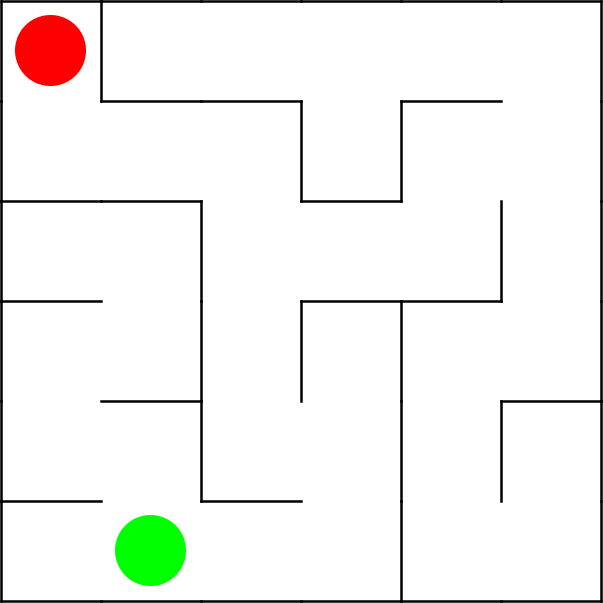
Als Motivation für die Lösung dieses Problems soll folgendes Beispiel dienen: Eine Person befindet sich in einem Labyrinth, und sucht einen Ausgang, indem sie alle möglichen Kreuzungen von Gängen in Augenschein nimmt. Übertragen auf die Graphentheorie, existieren hierfür zwei bekannte algorithmische Lösungsverfahren, die Hauptgegenstand dieser Vorlesung sind. In unserem Beispiel sind die Gänge des Labyrinths die Kanten und alle Kreuzugen die Knoten des Graphen.
Stellen wir uns vor, die eingeschlossene Person folgt einem bestimmten Gang solange, bis sie in eine Sackgasse gerät, zur letzten Kreuzung zurückkehrt und einem anderen Weg auf die gleiche Art verfolgt. Dieses systematische Vordringen in die "Tiefe" nennen wir Tiefensuche. Sucht jedoch eine Gruppe von Leuten den Ausgang, so ist es wahrscheinlicher, dass sie gemeinsam vom Startpunkt ausschwärmen in die "Breite" vordringen. Analog dazu sprechen wir von einer Breitensuche.
Am Ende des Kapitels wird es uns möglich sein, das Labyrinth-Problem und viele andere graphentheoretische Probleme mithilfe der beiden Algorithmen zu lösen.
Hinweis: Im Folgenden wird häufig von Suche die Rede sein, obwohl es sich meistens eher um einen Durchlauf handelt. Durch die Übernahme der englischen Begrifflichkeiten DFS und BFS (depth-first und breadth-first search) haben sich die Bezeichnungen Tiefen- und Breitensuche anstelle von -durchlauf eingebürgert. Wir hoffen, damit kein allzu große Verwirrung zu stiften.
Inhaltsverzeichnis |
Wiederholung
Zum Verständnis der später vorgestellten Graphenalgorithmen sind grundlegende Kenntnisse über Graphen und spezielle Datenstrukturen notwendig, die jedoch bereits Themen in vorigen Veranstaltungen waren und im Folgenden nur aufgefrischt werden sollen.
Graphrepräsentation
$\rightarrow$ siehe Vorlesung Graphrepräsentation
Kontrollfragen:
- Was ist der Unterschied zwischen gerichteten und ungerichteten Graphen?
- Welche Darstellungsformen für Graphen gibt es?
- Wie können diese im Computer realisiert werden?
- Welche ist am besten?
Bäume
$\rightarrow$ siehe Vorlesung Sortierte Folgen
Kontrollfragen:
- Was sind die Bestandteile eines Baumes?
- Welche Arten von Knoten gibt es?
- Was ist ein Pfad?
Datenstrukturen Stack und Queue
$\rightarrow$ siehe Vorlesung Prioritätswarteschlangen
Kontrollfragen:
- Nach welchem Prinzip arbeitet eine Warteschlange?
- Nach welchem Prinzip arbeitet ein Stack?
Grundlagen zum Graphendurchlauf
Allgemeiner Durchlauf-Algorithmus
Unsere zentrale Frage lautet: Wie können wir die Knoten eines Graphen durchlaufen, sodass jeder Knoten mindestens einmal besucht wird?
Um am Ende eine vernünftige Durchlaufordnung angeben zu können, die auch mit dem Computer ermittelbar sein sollte, überlegen wir uns folgendes Verfahren:
- Eingaben:
- zusammenhängender Graph $G$ als Adjazenzlisten- oder -matrixdarstellung
- eine Menge von Knoten $v \in V$ mit den Zuständen $unbesucht$ und $besucht$
- eine Arbeitsliste $L$, die besuchte aber noch nicht abgearbeitete Knoten beinhaltet.
- Algorithmus:
- Initialisierung: nur der Startknoten $v$ ist mit $besucht$ markiert und befindet sich in der Arbeitsliste $L$
- solange $L$ nicht leer ist:
- wähle einen Knoten $v$ aus $L$
- wähle und markiere einen unbesuchten Nachbarn $u$ von $v$ als besucht und speichere $u$ in die Arbeitsliste $L$
- falls $v$ keine unbesuchten Nachbarn besitzt, entferne $v$ aus $L$
Algorithmus: Graphendurchlauf_allgemein (Graph $G$, Knoten $v \in V(G)$, Arbeitsliste $L$)
end Graphendurchlauf_allgemein
Suchen wir im Graphen dagegen ein bestimmtes Element, so wie wir bei unserem Labyrinth-Problem nach dem Ausgang (Zielknoten) suchen, genügt es, den Algorithmus bis zum Auffinden des gesuchten Elements auszuführen und mit Ausgabe des Pfades bis zum Ziel terminieren zu lassen. Nachdem wir also das Ziel erreicht haben, ist es nicht nötig, den Graphen weiter zu durchlaufen, selbst wenn es noch unbesuchte Knoten gibt. Der Suchalgorithmus terminiert spätestens, wenn alle Knoten durchlaufen wurden, sodass sicher ist, dass das Element, falls es im Graphen enthalten ist, auch gefunden wird. In der Praxis ist diese Bedingung abhängig vom gewählten Verfahren nicht immer erfüllbar. Mehr dazu in den Abschnitten Breiten- und Tiefensuche.
Die Arbeitsliste $L$
Die Art und Weise wie die einzelnen besuchten Knoten in die Arbeitsliste $L$ eingefügt werden sollen, ist beim Graphendurchlauf von großer Bedeutung. Hierfür gibt es zwei Möglichkeiten.
Die Arbeitsliste als Stack
Wird die Arbeitsliste als Stack implementiert, wird jeder besuchte Knoten nach dem LIFO-Prinzip eines Stacks auf $L$ abgelegt.
Arbeitsweise:
- markiere den Startknoten $v$ als $besucht$ und legen ihn auf den leeren Stack ab
- solange der Stack nicht leer ist:
- ermittle alle unbesuchten Nachbarn des obersten Knotens $v$ im Stack und lege sie auf den Stack ab
- falls der oberste Knoten keine unbesuchten Nachbarn besitzt, entferne ihn aus dem Stack und fahre mit dem neuen ersten Element fort.
Mit dieser Implementierung lässt sich die Tiefensuche realisieren.
Die Arbeitsliste als Queue
Wird die Arbeitsliste dagegen als Queue implementiert, werden die besuchten Knoten nach dem FIFO-Prinzip einer Warteschlange an $L$ angefügt.
Arbeitsweise:
- markiere den Startknoten $v$ als $besucht$ und füge ihn in die leere Queue ein
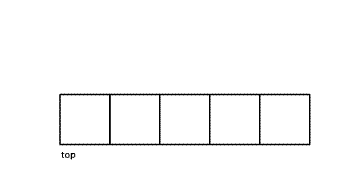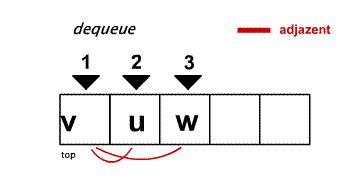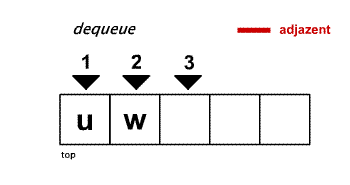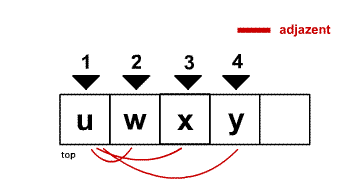
- solange die Queue nicht leer ist:
- ermittle alle unbesuchten Nachbarn des ersten Knotens $v$ in der Queue und hänge sie an die Warteschlange an
- falls $v$ keine unbesuchten Nachbarn besitzt, entferne $v$ aus der Queue und fahre mit dem neuen ersten Element fort
Mit dieser Implementation kann die Breitensuche realisiert werden.
Laufzeitverhalten
Mit welcher Laufzeit kann bei diesem Algorithmus gerechnet werden?
Relevant für den Algorithmus ist die Anzahl der Knoten und Kanten im Graphen. Daher ist die vom Verfahren benötigte Zeit ungeachtet der verwendeten Datenstruktur für die Arbeitsliste $L$ stets proportional zur Summe der Anzahl aller vom Startknoten erreichbaren Knoten und Kanten. Der Schleifendurchlauf im Funktionskörper führt stets gleich viele Schritte aus, wobei kein Knoten doppelt abgearbeitet wird. Wir notieren eine Maximallaufzeit von $\mathcal{O}\: (|V| + |E|)$ mit $V$ als Knoten- und $E$ als Kantenanzahl.
Zusammenhängende Graphen
Als Eingabe für den Durchlauf-Algorithmus haben wird einen zusammenhängenden Graphen angegeben. Wir fragen jetzt, wann ist ein Graph zusammenhängend bzw. wann ist er es nicht?
Definition: Ein Graph $G$ heißt zusammenhängend, wenn je zwei Knoten von $G$ verbindbar sind, d.h. es existiert ein Kantezug (Pfad) zwischen den beiden Knoten. Ein zusammenhängender Graph enthält keine isolierten Knoten.
Beispiele:
Ein Anwendungsbeispiel zur Zusammenhangsproblematik findet sich in vielen Städten: Einbahnstraßen. Befinden sich in einem Stadtteil besonders viele Einbahnstraßen, stellt sich als Autofahrer die Frage, ob man noch von jedem Ort aus jeden anderen Ort erreichen kann.
Ist ein Graph nicht zusammenhängend, kann man ihn in gewisse Komponenten (Teilgraphen) zerlegen, die unter sich zusammenhängend sind. Die Menge dieser Teilgraphen ergibt widerum den Graphen. Wir sprechen hier bei ungerichteten Graphen von sogenannten Zusammenhangskomponenten und bei gerichteten Graphen von starken Zusammenhangskomponenten (engl. strongly connected components, SCCs), deren Bestimmung wir an späterer Stelle kennenlernen werden. Besteht ein Graph aus nur einer Zusammenhangskomponenten, ist er zusammenhängend.
Unsere interne Graphenrepräsentation
Eine Vielzahl der nachfolgenden Algorithmen wollen wir einerseits durch Rechnung per Hand als auch mittels Computer umsetzen und anwenden. Der Vorteil hierfür liegt vorallem bei Berechnungen und Operationen auf sehr umfangreichen und dichten Graphen. Wir verwenden in allen Programmbeispielen ausschließlich die Programmiersprache JAVA, da wir mithilfe der Objektorientierung die einzelnen Sachverhalte einfach und verständlich modellieren können.
Knoten
Graph
Einige der in der Klassendefinition von Graph enthaltenen Methoden sollen an dieser Stelle nun getestet werden. Wir erstellen zwei Beispielgraphen jeweils unterschiedlichen Typs und mit unterschiedlicher Knoten- und Kantenanzahl. Des Weiteren lassen wir uns die zugehörigen Adjazenzmatrizen anzeigen.
Übungsaufgaben:
- Zeichnen Sie die beiden Graphen $G_{bsp01}$ und $G_{bsp02}$ per Hand.
- Sind beide Graphen zusammenhängend?
Tiefensuche
Die Tiefensuche beginnt mit einem beliebigen Startknoten $u \in V(G)$ und folgt einer mit $u$ adjazenten Kante, bis zum nächsten Knoten $v\in V(G)$, der noch nicht besucht wurde (unmarkiert ist). Von diesem aus wird wieder ein benachbarter Knoten gesucht. Man folgt also solange einem Kantenzug, bis man ein Blatt erreicht hat. Alle dabei entdeckten Knoten werden markiert.
Nun verfolgt man den entstandenen Kantenzug solange zurück(backtracing), bis man einen Knoten findet, mit dem noch unbesuchte Knoten verbunden sind. Wird solch ein Knoten entdeckt, wählt man ihn als neuen Startknoten und folgt wieder seinen adjazenten Kanten.
Anschließend wird solange ein neuer unmarkierter Knoten als Startknoten gewählt und abgearbeitet, bis alle Knoten markiert sind.
Auf diese Weise entsteht ein Suchwald. Obwohl der Algorithmus einen Graphen $G$ immer vollständig abarbeitet, können abhänig vom Startknoten und der konkreten Implementierung verschiedene Suchwälder entstehen. Meistens ist aber jeder Wald sinnvoll verwendbar.
Iterativ mit Stack
Abgewandelt vom allgemeinen Durchlaufalgorithmus kann man einen Graphen in die Tiefe untersuchen, wenn man die besuchten Knoten temporär auf einen Stack ablegt und bei ihrer Abarbeitung nach dem LIFO-Prinzip wieder aus dem Stapel entfernt. So ist sichergestellt, dass einem neu entdeckten Knoten zuerst gefolgt wird. Dieses iterative Verfahren funktioniert nur vollständig auf zusammenhängenden Graphen (bei Digraphen mit starkem Zusammmenhang), da es nur die vom Startknoten aus erreichbaren Knoten untersucht, d.h. wählt man z.B. in einem Digraphen einen ungünstigen Startknoten, so werden unter Umständen nicht alle Knoten entdeckt. Wichtig ist außerdem, dass bereits besuchte Knoten unbedingt mit einer gesonderten Markierung zu versehen sind, da sich der Durchlauf-Algorithmus sonst in Zyklen und unendlichen Pfaden verlieren kann. Bei unserer Implementation ist so ein Zyklentest bereits integriert.
Algorithmus: Tiefendurchlauf (zusammenhängender Graph $G$, Knoten $v \in V(G)$, Stack $S$)
end Tiefendurchlauf
Rekursive DFS
- Eingaben:
- Graph $G$ als Adjazenzlisten- oder -matrixdarstellung
- Eine Menge von Knoten $V(G)$mit den Zuständen:
- $farbe=weiss$ für unbesuchte Knoten
- $farbe=grau$ für besuchte Knoten
- $farbe=schwarz$ für abgeschlossene Knoten
- $\pi=nil$ (der Vorgänger)
- $d[u]=0$ (die Zeit der Entdeckung)
- $f[u]=0$ (die Zeit des Abschließens)
Algorithmus: DFSrek (Graph $G$)
end DFSrekAlgorithmus: DFSvisit ($u$)
end DFSvisit
Klassifizierung der Kanten
Wie schon beschrieben erzeugt die DFS einen vom Durchlauf abhängigen Tiefensuchwald. Man kann nun jede Kante einem von vier Typen zuordnen, entsprechend ihrer Sondierung in der DFS
- Typen:
- Baumkanten sind Kanten im Tiefensuchwald $G_\pi$ . Kante $(u,v)$ ist eine Baumkante, falls $v$ bei der Sondierung der Kante $(u,v)$ entdeckt wurde
- Rückwärtskanten sind Kanten $(u,v)$, die $u$ mit einem Vorfahren $v$ im Tiefensuchbaum verbinden. Ebenso Schlingen in gerichteten Graphen
- Vorwärtskanten sind alle nicht-Baumkanten $(u,v)$ die $u$ mit einem Nachfahren $v$ im Tiefensuchbaum verbinden
- Querkanten sind alle verbliebenen Kanten, solange nicht der eine Vorfahre des anderen ist
Breitensuche
Während die Tiefensuche zunächst einem Pfad bis zur nächsten Sackgasse folgt und dabei recht unbalancierte Suchwälder erzeugt, kommt die Breiten einem vorsichtigerem Voranschreiten gleich. Bevor das Verfahren einen weiteren Schritt in die Tiefe unternimmt, werden zunächst alle Knoten auf der momentanen Ebene (engl. Layer) besucht. Von einem Startknoten $v$ werden also zunächst alle Knoten mit dem Abstand $d(v)=1$, d.h. alle unmittelbaren Nachbarknoten untersucht und in den nächsten Schritten jeweils alle Knoten mit dem Abstand $d+1$, d.h. alle Nachfolger der Nachfolger.
Dieses schichtweise Voranschreiten hat mehrere Vorteile gegenüber der Tiefensuche:
- Es werden ausbalancierte Suchwälder erzeugt.
- Es wird immer der kürzeste Weg von einem Knoten zum nächsten gefunden.
- Es wird sichergestellt, dass das Verfahren mit Sicherheit bei einer Knotensuche terminiert, falls sich das gesuchte Element im Graphen befinden sollte. Bei der Tiefensuche kann es dagegen passieren, bei Zyklen eine Endlosschleife zu produzieren, falls man bei der Implementation das Auftreten von Kreisen nicht berücksichtigt.
Um alle Knoten in einem Graphen zu durchlaufen, benötigt die Breitensuche jedoch im Allgemeinen mehr Schritte, also einen höheren Speicherbedarf, als die Tiefensuche, besitzt aber dennoch die Komplexität $\mathcal{O}\: (|V| + |E|)$.
Abgeleitet von der allgemeinen Durchlaufvorschrift unter Benutzung einer Warteschlange $Q$ als Arbeitsliste, beschreibt folgender Algorithmus die Arbeitsweise der Breitensuche.
Algorithmus: Breitendurchlauf (Graph $G$, Knoten $v \in V(G)$, Queue $Q$)
end Breitendurchlauf
Der Algorithmus kann aufgrund seiner klaren Struktur sehr einfach in Programmcode übertragen werden. Wie wir bereits bei der DFS-Implementierung mit Stack bemerkt haben, können wir mit diesem Algorithmus nur zusammenhängende Graphen durchlaufen.
Übungsaufgaben:
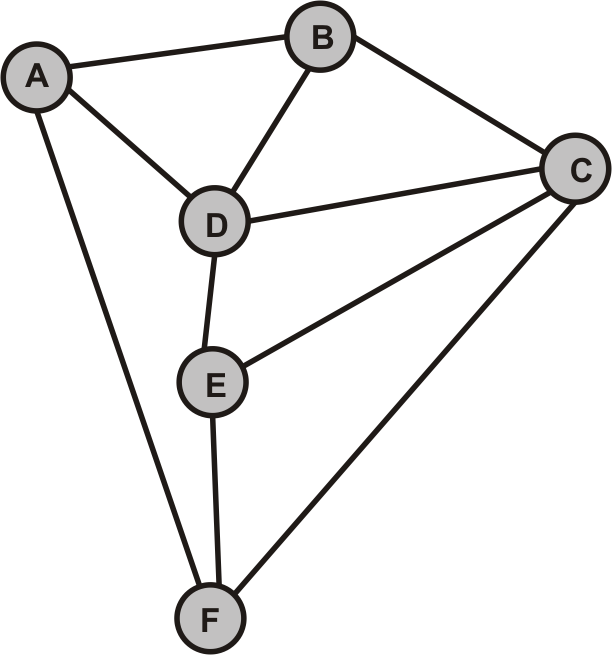
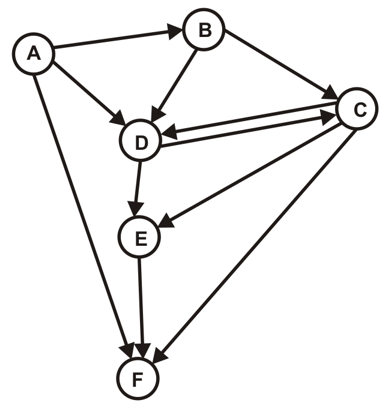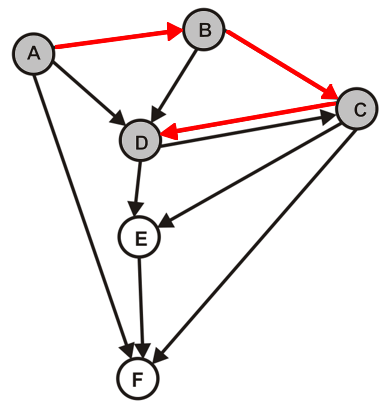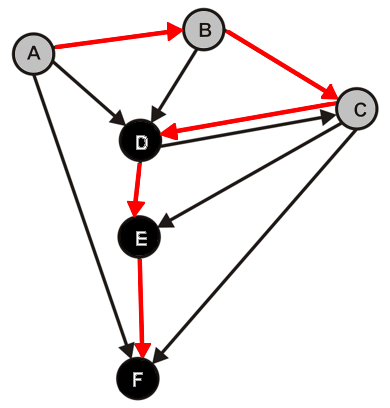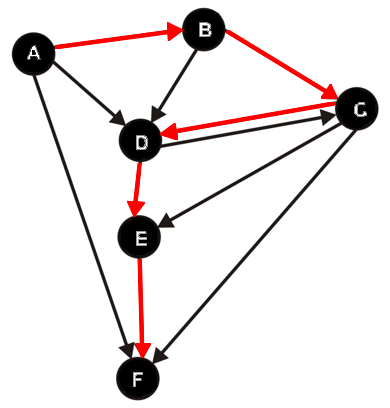
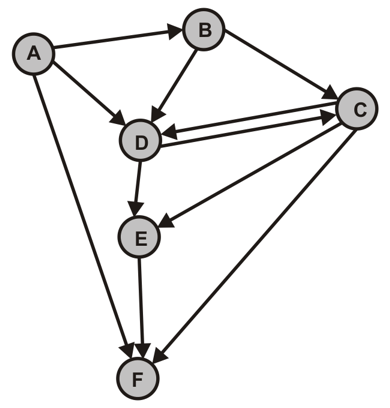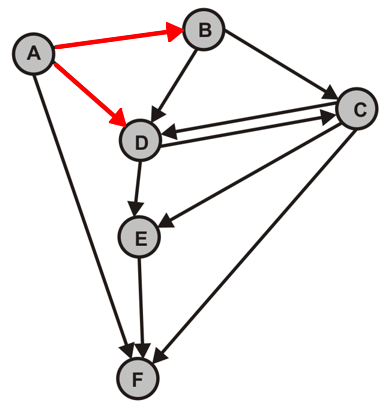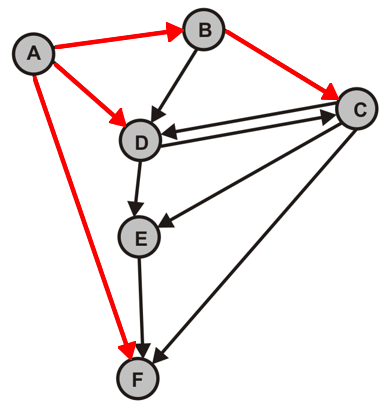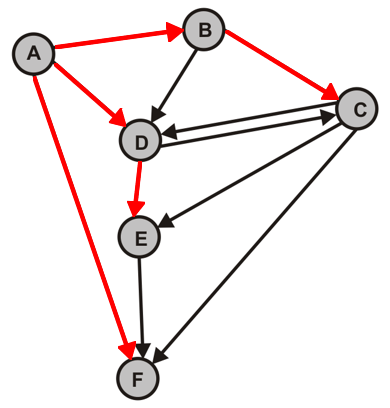
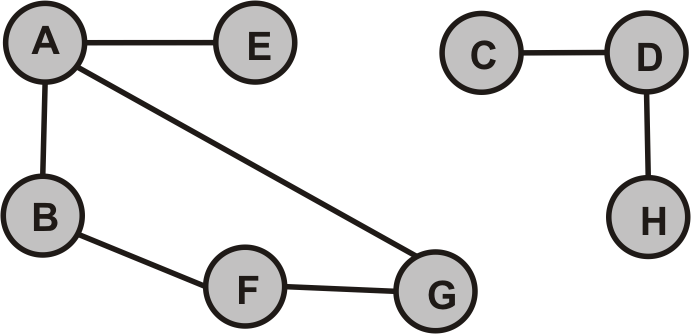
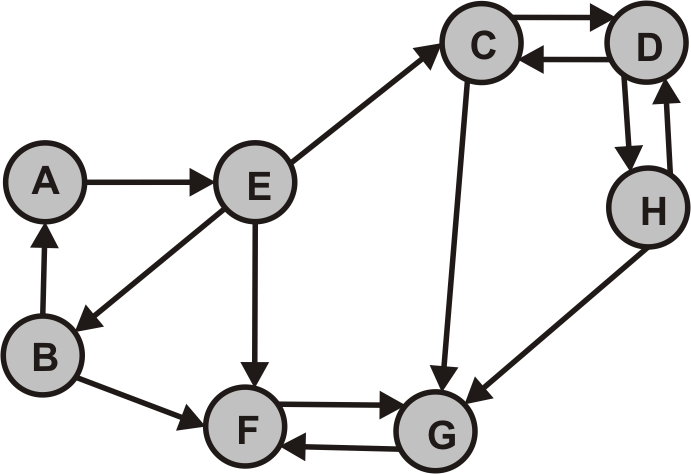
- Durchlaufen Sie die folgenden Graphen jeweils vom Knoten A zunächst per Hand und überprüfen Sie Ihre Lösung anschließend mit dem Programm.
- $G_1$
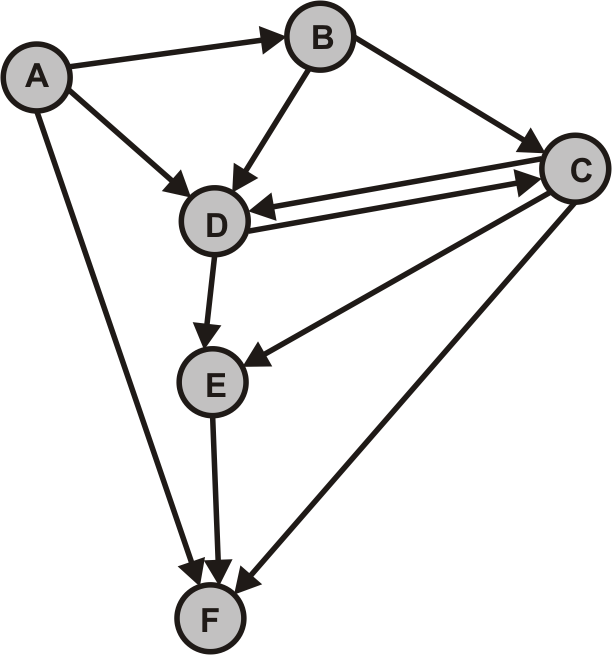
- $G_2$ (Was fällt bei diesem Graphen auf? Interpretieren Sie die Programmausgabe.)
- Testen Sie das BFS-Applet auf: Lupinho.de mit
- einem gerichteten Graphen.
- einen unzusammenhängenden Graphen.
Hilfe zu Bedienung des Applet erhalten Sie hier.
Kombination von Tiefen- und Breitensuche
Beide Durchlaufverfahren haben ihre Vor- und Nachteile und sind je nach Problemstellung günstig. Nachfolgend seien nochmals Tiefen- und Breitensuche gegenübergestellt.
| Tiefensuche | Breitensuche | |
| Laufzeit | $\mathcal{O}\: (|V| + |E|)$ | $\mathcal{O}\: (|V| + |E|)$ |
| Speicherverbrauch | moderat | u.U. sehr umfangreich |
| Einsatzgebiete | Labyrinthsuche Bestimmung von SCCs |
Ermittlung kürzester Pfade |
| Vorteile | geringer Speicherverbrauch | kürzeste Pfade vollständig |
| Nachteile | unvollständig bei Zyklen und endlosen Pfaden | hoher Speicherbedarf |
Es existiert nun ein Verfahren, das die Vorteile beider Durchlaufalgorithmen vereint, d.h. bei optimalem Speicherplatzverbrauch wird immer ein Ergebnis gefunden, ohne sich in Zyklen oder sehr langen Pfaden zu verlieren, falls dies nicht durch die Implementierung abgefangen wird. Wir sprechen in diesem Fall von einer tiefenbeschränkten Suche.
Das Prinzip besteht darin, eine maximal zulässige Suchtiefe anzugeben, ab der die DFS abbricht. Damit ist sichergestellt, dass der Suchvorgang in jedem Fall terminiert. Die Laufzeit liegt weiterhin bei $\mathcal{O}\: (|V| + |E|)$.
Anwendung/ weiterführende Themen
Topologisches Sortieren
Die Topologische Sortierung reiht alle Knoten eines azyklischen Graphen $G$ in einer Linie auf. $u$ ligt vor $v$ falls es in $G$ eine Kante $(u,v)$ gibt. Alle gerichteten Kanten zeigen nun von links nach rechts.
Topologisch sortierte Knoten eines Graphen $G$ sind in der umkehrten Reihenfolge ihrer Endzeiten in der DFS angeordnet.
Topological-Sort($G$)
- DFS($G$) aufrufen um die Endzeiten $f[u]$ für alle Knoten $u$ zu bekommen
- jeden abgearbeiteten Knoten am Kopf einer Liste $L$ einfügen
- $L$ ist nun topologisch sortiert
Die topologische Sortierung wird zur Darstellung der Priorität von Ereignissen verwendet.
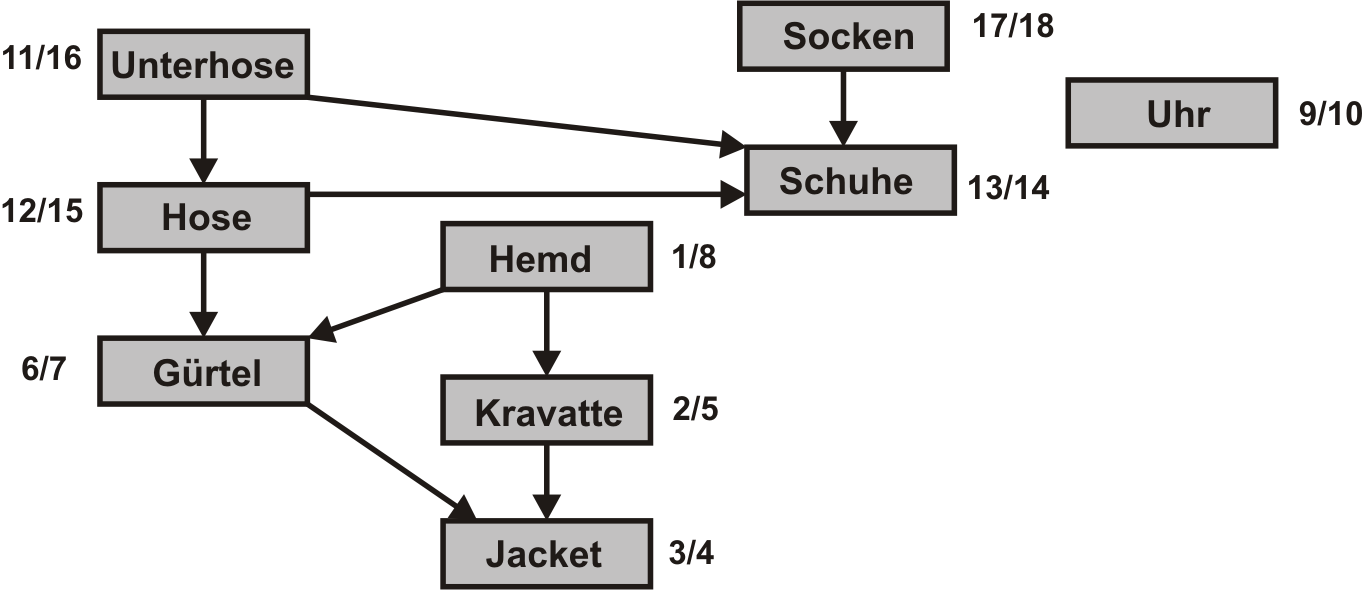
Das Beispiel:
Professor Bumstead führt eine topologische Sortierung seiner Kleidung durch, wenn er sich anzieht.
Wenn man entwas mit den Startwerten der DFS experimentiert, sieht man, dass sich aufgrund der verschiedenen Suchwälder auch verschiedene Topologische sortierungen einstellen. Es wird aber nie z.B. das Jacket vor der Kravatte angezogen. Die Position von isolierten Knoten(der Uhr) ist hingegen beliebig.
Euler und CPP
Eulerpfad/-kreis
Das Eulerkreis Problem hat seinen Ursprung in dem Vorhaben von Leonhard Eulers, alle fünf Stadtteile von Königsberg zu besuchen, dabei jede Brücke aber nur einmal zu überqueren und am Startpunkt wieder anzukommen.
Siehe dazu:Königsberger Brückenproblem
Bevor man versucht einen Eulerkreis zu finden, wird der Graph $G$ geprüft, ob er überhaupt einen zulässt. Dazu ermittelt man den Grad aller Knoten und zählt wieviele geraden/ungeraden Grades sind.
- eulersch wenn:
- stark zusammenhängend
- bei jedem Knoten ist Eingangsgrad=Ausgangsgrad
- zusammenhängend
- jeder Knoten hat geraden Grad
- wähle beliebigen Startknoten $u \in V(G)$
- wähle eine an $u$ angrenzende Kante, wähle zuerst Kanten die keine Brückenkanten sind
- füge die Kante der Liste des Eulerkreises hinzu, Kante markieren
- den anderen Knoten der gewählten Kante als neuen aktuellen knoten wählen
- existieren noch unmarkierte Kanten wieder zu Schritt 2
- Testen Sie das Applet auf Cut-the-knot.org und geben Sie zu den ersten beiden Graphen jeweils an:
- einen Eulerkreis
- einen Eulerpfad
- einen Hamiltonkreis
- einen Hamiltonpfad
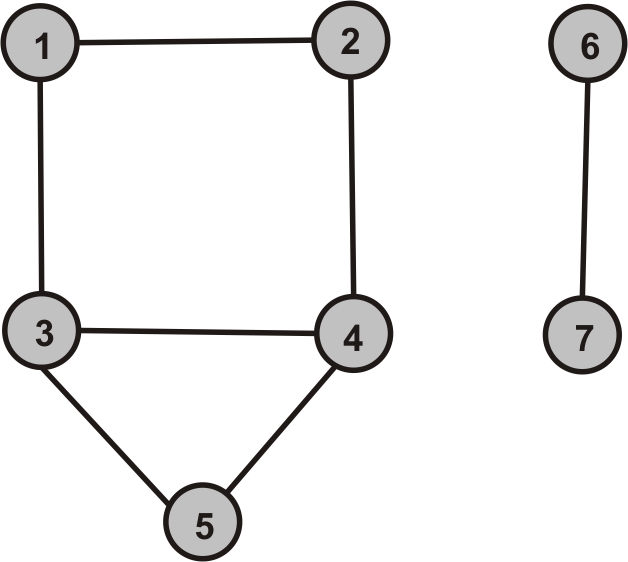
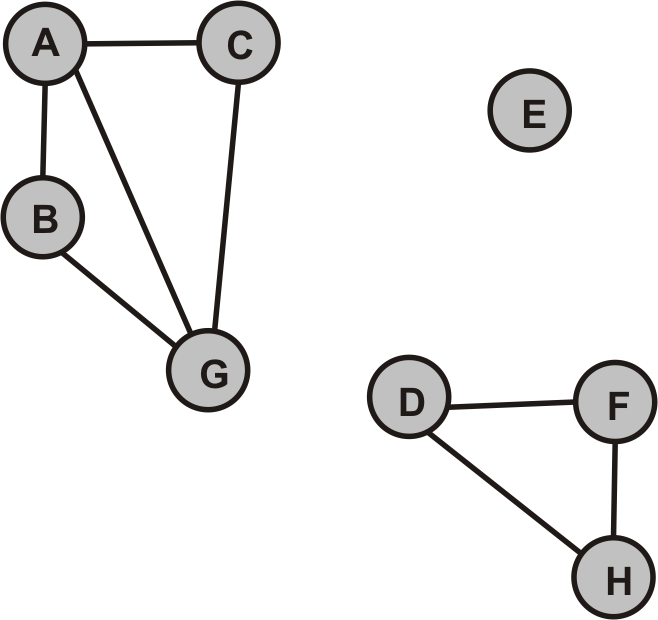
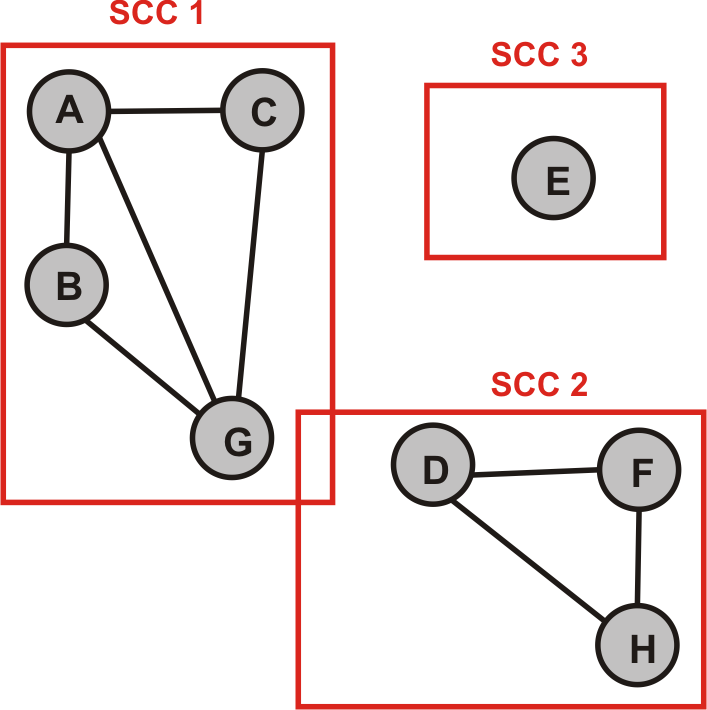
- Ermitteln Sie die Zusammenhangskomponenten des folgenden Graphen:
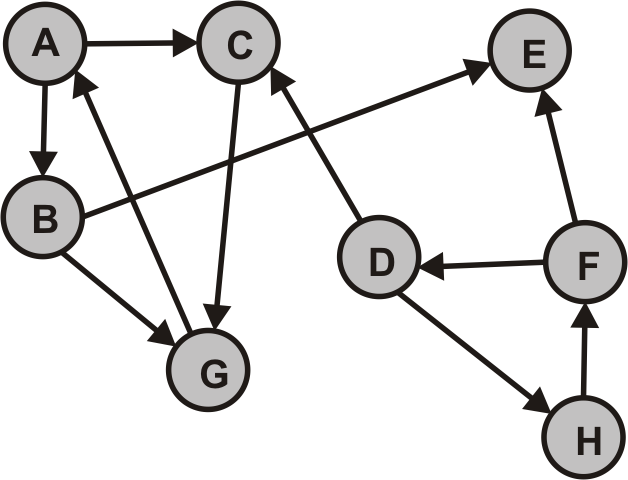
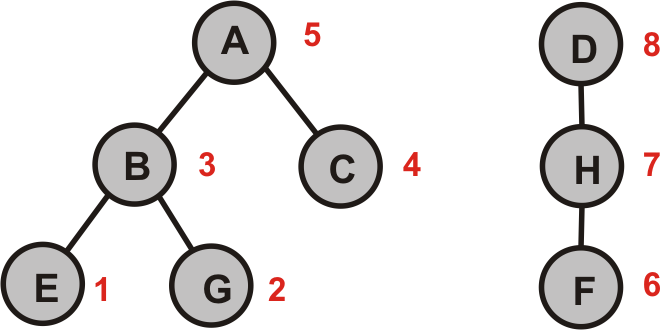
- Berechne mit einer Tiefensuche auf den Graphen $G$ alle DFS-Wälder von $G$
- Nummeriere die Knoten in der Reihenfolge ihrer topologischen Sortierung
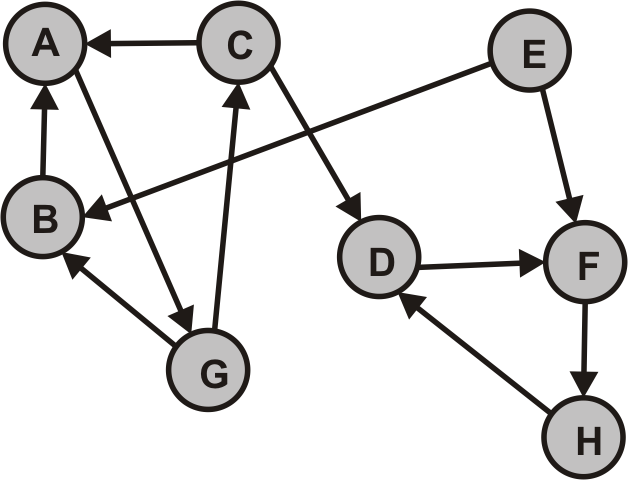
- Konstruieren den zu $G$ transponierten Graphen $G_T$, indem bei der jeder Kante aus $G$ die Richtung umgekehrt wird
- Berechne mit einer Tiefensuche nun alle DFS-Wälder von $G_T$, wähle dafür bei jedem Durchlauf den Knoten mit der höchsten Nummerierung aus der topologischen Sortierung als Startknoten
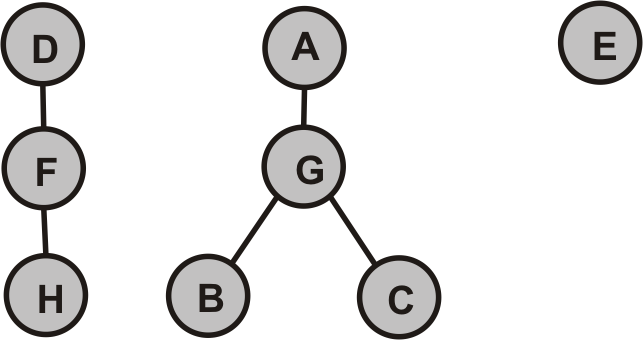
- Jeder der entstehenden Bäume bildet die Knotenmenge einer starken Zusammenhangskomponente von $G$
- Wir wenden zunächst eine Tiefensuche auf $G$ an, erzeugen alle DFS-Wälder von $G$ und nummerieren jeden Knoten gemäß seiner topologischen Sortierung.
- Wir bilden den transponierten Graphen $G_T$.
- Nun wenden wir die Tiefensuche auf $G_T$ an, wobei wir mit Knoten mit dem höchsten Wert in der topologische Sortierung beginnen und ermitteln alle DFS-Wälder
- Als Resultat erhalten wir die SCCs von $G$
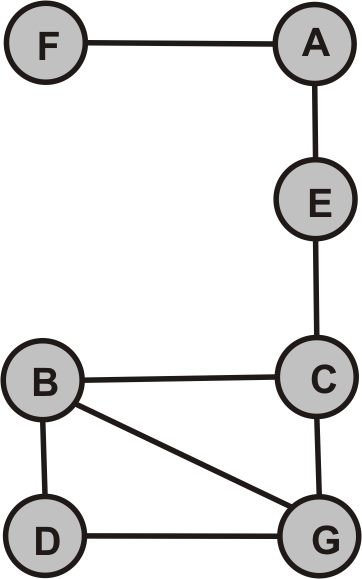
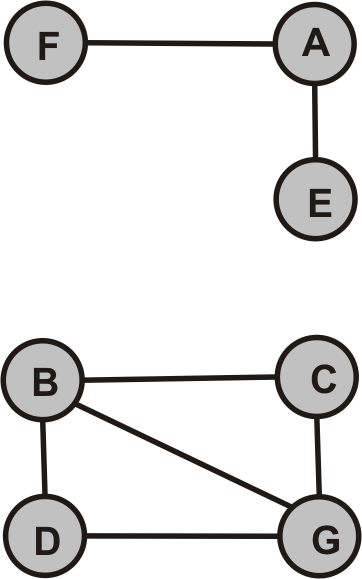
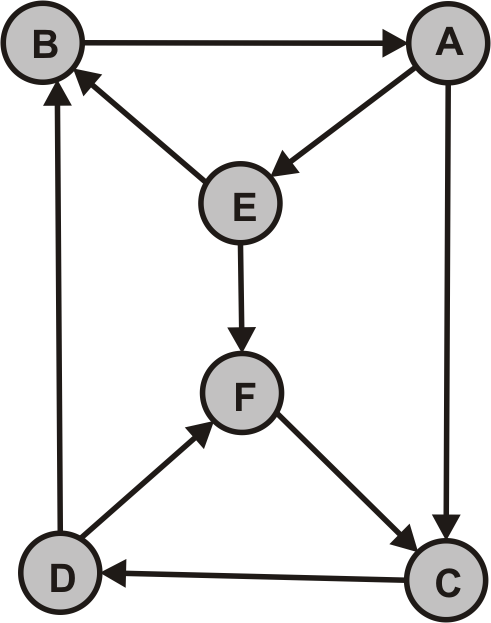
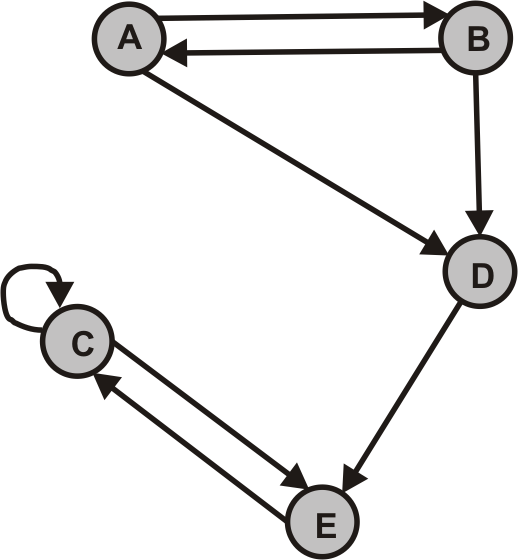
- Durchlaufen Sie beide Graphen mittels Tiefensuche per Hand. Starten Sie jeweils beim Knoten A.
- DFS iterativ
- DFS rekursiv. Sortieren Sie topologisch.
- Durchlaufen Sie beide Graphen mittels Breitensuche.
- Sind die beiden Graphen zusammenhängend?
- Falls nein, bestimmen Sie jeweils die Zusammenhangskomponenten.
- Existiert in den beiden Graphen
- ein Eulerkreis/ -pfad?
- ein Hamiltonkreis/ -pfad?
- gerichtet und
- ungerichtet und
Wenn zwei oder kein Knoten ungeraden Grad haben, eistiert in einem ungerichteten, zusammenhängenden Graphen ein Eulerweg/pfad.
Auch wenn schnellere Algorithmen gibt(z.B. der Algorithmus von Hierholzer) wird hier der Algorithmus von Fleury kurz vorgestellt:
- Algorithmus von Fleury
Laufzeit: $\mathcal{O}(|E|^2)$ $\leftarrow$ (Brückenkante finden $\mathcal{O}(|E|)$, Kanten absuchen $\mathcal{O}(|E|)$, Iterationen $|E|$
Vollständiger Graph mit 5 Ecken: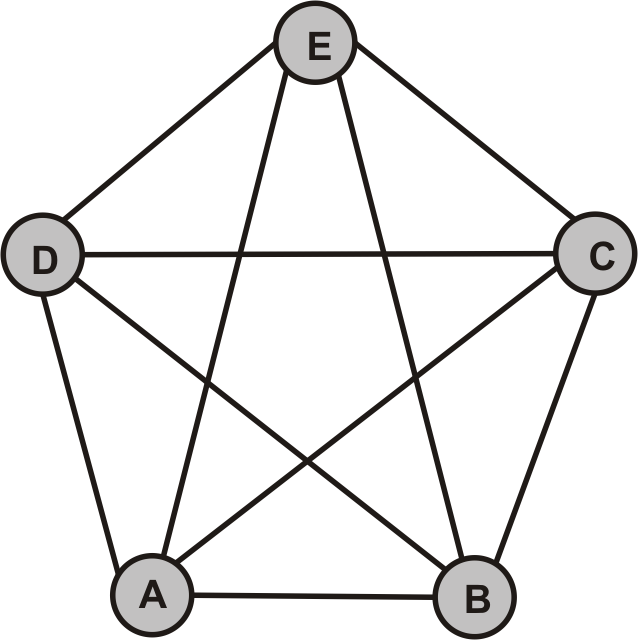
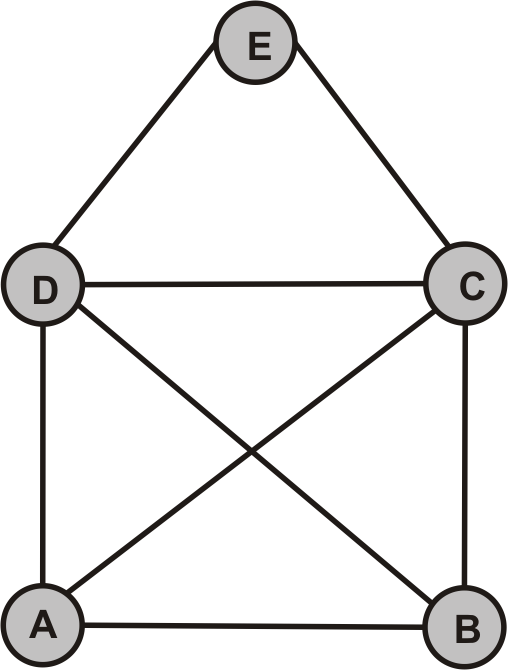
CPP
Das Chinese Postman Problem (dt. Briefträgerproblem) erhielt seinen Namen vom chinesischen Mathematiker Mei Ko Kwan, der das Problem erstmals 1962 untersuchte.
Inhalt des Problems ist die Frage nach dem besten Weg um Briefe zuzustellen. Jede Straße wird hierbei als Kante und jede Straßenkreuzung als Knoten in einem Straßennetzwerk(Graph) modelliert. Der Postbote muss nun jede Straße(Kante) genau einmal ablaufen, um alle Adressaten zu erreichen und dennoch nicht zu viel zu laufen.
Damit kann man das CPP lösen, indem man einen Eulerkreis findet.
Leider sind reale Straßennetze nicht immer eulersch, das Thema soll hier jedoch nicht weiter vertieft werden.
Hamilton und TSP
Das Hamiltonkreis-Problem ähnelt auf den ersten Blick dem eben beschriebenen Sachverhalt des Eulerkreis-Problems, sollte jedoch nicht mit diesem verwechselt werden, da sowohl Definition als auch algorithmische Lösungsansätze vollkommen verschieden sind.
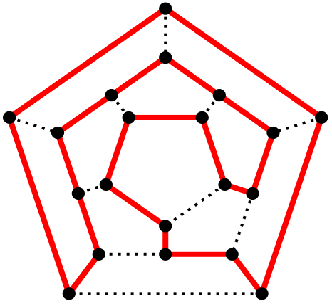
Das Problem geht auf ein Spiel namens "Around the world" zurück, das 1859 von William Hamilton vorgeschlagen wurde. Ziel des Spiels war es, entlang der Kanten eines Dodekaeders (dessen Knoten mit Städten benannt wurden) eine Rundreise zu unternehmen, wobei jede Stadt nur einmal besucht werden darf. Übertragen auf die Graphentheorie suchen wir also einen Kreis, der jeden Punkt genau einmal enthält. Das heute sehr oft diskutierte Travelling Salesman Problem (TSP), bei dem ein Handelsreisender eine Rundreise durch eine Anzahl von Städten unternimmt, wobei er jede Stadt nur einmal besucht und am Ende wieder an der ersten Stadt ankommen soll, entspringt dem Spiel von Hamilton. Anders als beim Eulerkreis-Problem existieren für das Hamiltonkreis-Problem weder ein effizienter Algorithmus noch eine endgültige Kennzeichnung, wann ein Graph hamiltonsch ist. Bisher gibt es nur eine Ansammlung von hinreichenden Bedingungen, nach denen ein Graph offenbar hamiltonsch ist.
Analog zum Hamiltonkreis gibt es auch sogenannte Hamiltonpfade. In einem Hamiltonpfad darf jeder Knoten nur einmal durchlaufen werden, wobei der Startknoten nicht der Zielknoten sein muss.
Die Lösung des TSP oder des Hamiltonkreis-Problems soll an dieser Stelle nicht vorgenommen werden. Wir verweisen lediglich auf kommende Lehrveranstaltungen.
Knobelaufgabe
Starke Zusammenhangskomponenten
Wie wir bereits wissen, lässt sich ein unzusammenhängender Graph in Teilgraphen zerlegen, die jeweils zusammenhängend sind, d.h. jeder Knoten in diesem Teilgraphen ist von jedem anderen Knoten des Teilgraphen erreichbar. Diese Teilgraphen nennen wir auch Zusammenhangskomponenten. Schlimmstenfalls besteht ein Graph aus $V$ Zusammmenhangskomponenten mit $V$ als Knotenanzahl, falls keine Kantenüge zwischen den Knoten existieren.
Wir müssen an dieser Stelle zwei konkrete Fälle unterscheiden: Zusammenhangskomponenten in ungerichteten und gerichteten Graphen.
Ungerichtete Graphen
Der Zusammenhangsbegriff für ungerichtete Graphen wurde bereits an früherer Stelle geklärt. Wir werden nun einen Algorithmus zur Bestimmung von Zusammenhangskomponenten angeben, der zum Durchlaufen des Graphen die rekursive Tiefensuche verwendet. Wenden wir diese auf einen unzusammenhängenden Graphen an, werden zunächst nur diejenigen Knoten durchlaufen, die vom Startknoten aus erreichbar sind. Der dadurch entstandene Teilgraph ist unsere ersten Zusammenhangskomponente. Danach wird von den restlichen Knoten ein neuer Startknoten ausgewählt und das Verfahren wiederholt.
Der nachfolgende Algorithmus markiert jeden Knoten mit einer Komponentennummer $c$, die bei jedem Neustart der Tiefensuche inkrementiert wird und am Ende die Anzahl aller Zusammenhangskomponenten im Graphen angibt. Bei der Initialisierung ist jeder Knoten unmarkiert.
Algorithmus: Zusammenhangskomponenten(ungerichteter Graph $G$, Knoten $v \in V(G)$, Zähler c)
end Zusammenhangskomponenten
Algorithmus: tiefensuche(Knoten $v \in V(G)$, Zähler c)
end tiefensuche
Testen wir nun unseren Algorithmus implementiert als Funktion connectedComponents() mit einem Beispielgraphen.
Übungsaufgabe:
Gerichtete Graphen
Unser einfacher Algorithmus zur Ermittlung der Zusammenhangskomponenten in ungerichteten Graphen funktioniert für Digraphen leider nicht, da wir hier den Zusammenhangsbegriff etwas strenger fassen müssen. Während in einem ungerichteten Graphen zwei Knoten bereits als erreichbar gelten, wenn sie durch eine einfache Kante verbunden sind, so muss in einem Digraphen die Richtung der Kante beachtet werden. Aufgrund dieser stärkeren Eingrenzung wird ein zusammenhängender Digraph als stark zusammenhängend bezeichnet. Enthält ein Digraph starke Zusammenhangskomponenten (strongly connected components, SCCs), bedeutet das, dass er aus mehreren Teilgraphen besteht, die jeweils stark zusammenhängend sind. Isolierte Knoten sind ebenfalls SCCs, da jeder Knoten von sich selbst aus erreichbar ist.
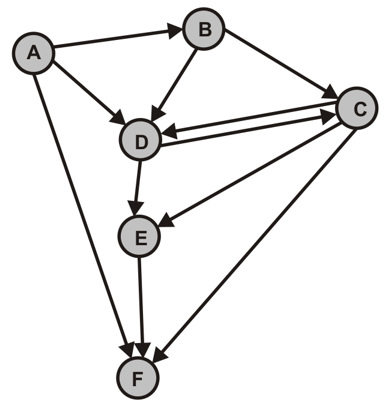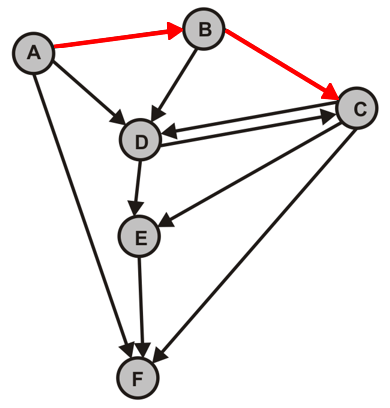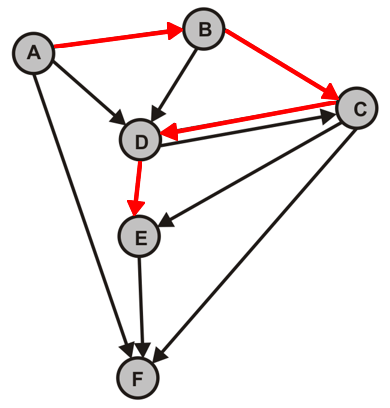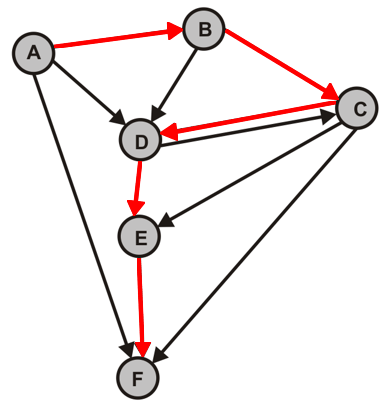
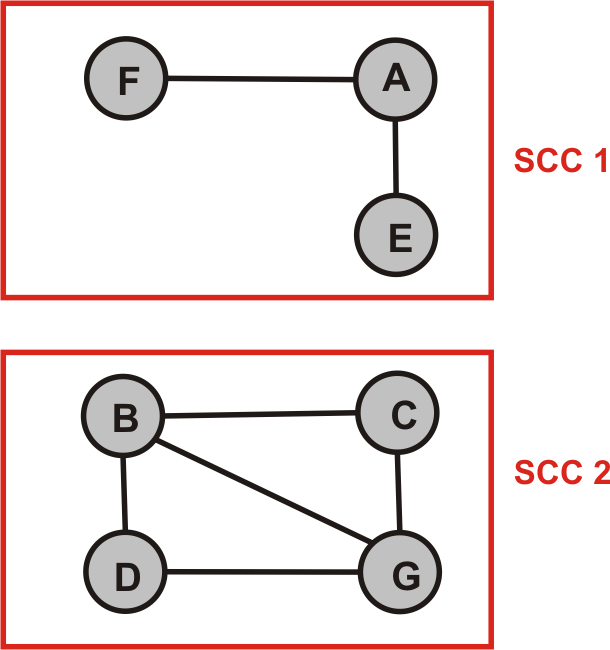
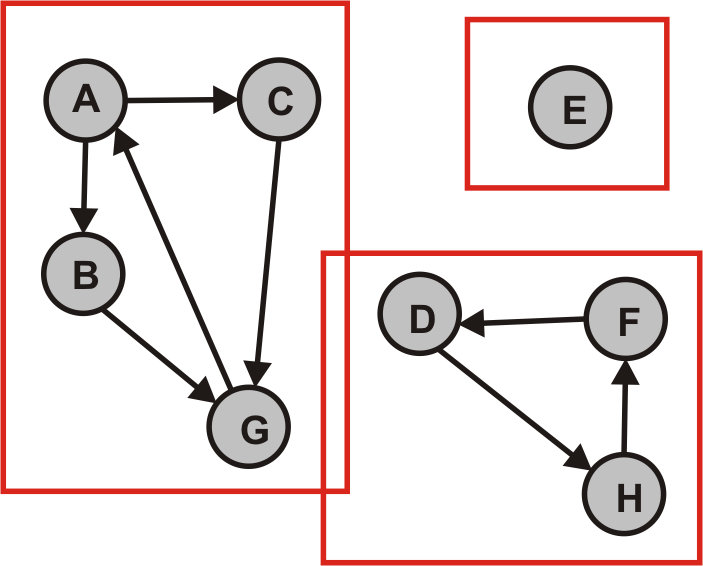
Zur Bestimmung der SCCs in einem Digraphen verwenden wir folgenden DFS-basierten Algorithmus:
Beispiel: Gegeben sei der obige gerichtete Graph $G$.
Komplexe Übungsaufgabe
Gegeben seien folgende Graphen $G_1$ und $G_2$: