Abstrakte Datentypen
Aus ProgrammingWiki
Inhaltsverzeichnis |
Effizienz-beeinflussende Faktoren
- Wahl passender abstrakter Datentypen (ADT), z.B. Stapel, Liste, Feld, Hashtable, Warteschlange, Graph, Heap usw.
- Entwurf effizienter Algorithmen, die diese ADT (und die zugehörigen Operationen) verwenden, z.B. Such- und
Sortierverfahren, Algorithmen auf Graphen usw. (z.B. HORNER-Schema, Schnelle Matrixmultiplikation)
- Geschickte Implementierung dieser Algorithmen
- Effiziente Implementierung der ADT durch geeignete Wahl konkreter Datenstrukturen, z.B. ADT Stapel mit einfach/mehrfach verketteten Listen oder mit Feldern implementieren (evtl. bereits in PS enthalten)
Ein Abstrakter Datentyp (ADT) ist ein theoretisches Konzept, mit dem ein Datentyp unabhängig von dessen Implementation, z.B. mittels konkreter Datentypen einer bestimmten Programmiersprache, definiert wird. Zur formalen Spezifikation gehören eine Signatur $\Sigma$ (Syntax) und eine Menge von Axiomen $\Phi$ (Semantik).
Definition: Die Signatur $\Sigma$ eines ADT ist ein Paar $\Sigma = (S, \Omega)$.
- $S$ ist die Menge aller Wertemengen (Sorten), die in den Operationen vorkommen dürfen.
- $\Omega$ enthält die Schnittstellenbeschreibungen aller Operationen (Funktionen), die der ADT kennt und nach außen (Schnittstelle) anbietet.
In $\Omega$ werden die (bedeutungslosen) Namen verwendet, um die Wertemengen der Parameter und die der Ergebnisse der Operationen zu beschrieben. Die Division von natürlichen Zahlen kann z.B. folgendermaßen dargestellt werden: $\text{div}: \mathbb{N} \div \mathbb{N} \to \mathbb{Q}^+$, wobei die verwendeten Sortennamen zunächst ohne Bedeutung sind. (Zur grafischen Darstellung kann man "Trichterbilder" verwenden: Im Beispiel $\text{div}$ gibt es zwei Eingabe- und einen Ausgabetrichter.)
Die Signatur $\Sigma$ eines ADT stellt dabei eine abstrakte Algebra dar. Das Konzept ist analog zu algebraischen Strukturen aus der (mathematischen) Algebra, wie Gruppen, Ringe oder Körper.
Definition: Die Axiome $\Phi$ eines ADT sind eine Menge von Gleichungen, die die Operationen in ihrer Wirkung beschreiben. Dabei handelt es sich um deskriptive Spezifikationen.
Durch die Axiome wird die Semantik der Operationen beschrieben. Ein ADT beschreibt demzufolge WAS die Operationen bewirken aber nicht WIE sie es umsetzen.
Durch die Wahl konkreter Datentypen (einer Programmiersprache) und implementierter Operationen (Funktionen; Prozeduren) mit Daten der gewählten Typen entsteht aus dem abstrakten ein konkreter Datentyp. Die Axiome wirken wie ein "Pflichtenheft" für ADT-Implementierer: Die gewählte Implementation muss den Axiomen vollständig gehorchen.
Die getroffene Wahl des konkreten Datentyps wirkt sich natürlich auf die Effizienz des betreffenden Programms aus.
Beispiele
Boolean
Die Menge der Booleans umfasst genau zwei Elemente, nämlich $\text{true}$ und $\text{false}$. Darüber hinaus werden in dieser Algebra die Operationen Negation $\neg$, Konjunktion $\land$ und Disjunktion $\lor$ definiert. Die Signaturen lassen erkennen, dass es drei einstellige und zwei zweistellige Operationen gibt.
$$ \begin{align*} S = \{ &\text{Boolean} \} \\ \Omega = \{ &\text{true}: \to \text{Boolean}, \\ &\text{false}: \to \text{Boolean} \\ &\neg : \text{Boolean} \to \text{Boolean} \\ &\land : \text{Boolean} \times \text{Boolean} \to \text{Boolean} \\ &\lor : \text{Boolean} \times \text{Boolean} \to \text{Boolean} \} \\ \Phi = \{ &\text{false} \land x = \text{false} \\ &x \land \text{false} = \text{false} \\ &\text{true} \land \text{true} = \text{true} \\ &\text{true} \land x = x \\ &x \land \text{true} = x \\ &\text{true} \lor x = \text{true} \\ &x \lor \text{true} = \text{true} \\ &\text{false} \lor \text{false} = \text{false} \\ &\text{false} \lor x = x \\ &x \lor \text{false} = x \\ &\neg \text{false} = \text{true} \\ &\neg \text{true} = \text{false} \} \\ \end{align*} $$
Stack
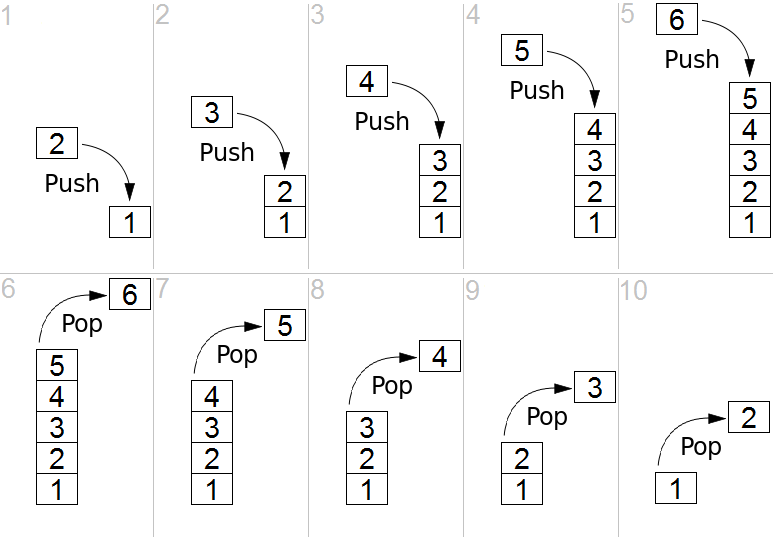
Wir beginnen mit einer informellen Beschreibung. Die beiden charakteristischen Operationen eines Stacks (Stapels) sind:
- push, welche ein Element zum Stack hinzufügt, und
- pop, welches das oberste Element (den top of stack) entfernt.
Dabei werden die Elemente aufeinander gestapelt. Bei der pop-Operation wird das zuletzt hinzugefügte Element wieder entfernt. Aufgrund dieser Reihenfolge ergibt sich der Begriff LIFO (last in, first out), welcher im Zusammenhang mit Stacks verwendet wird.
In der folgenden Definition finden sich noch weitere Operationen.
$$ \begin{align*} S = \{ & \text{Stack}, \text{Element} \} \\ \Omega = \{ &\text{create}: \to \text{Stack} \\ &\text{push}: \text{Stack} \times \text{Element} \to \text{Stack} \\ &\text{pop}: \text{Stack} \setminus \{ \epsilon \} \to \text{Stack} \\ &\text{top}: \text{Stack} \setminus \{ \epsilon \} \to \text{Element} \\ &\text{empty}: \text{Stack} \to \{ \text{true},\text{false}\} \} \\ \Phi = \{ &\text{create}() = \epsilon \\ &\text{empty}(\epsilon) = \text{true} \\ &\text{empty}(\text{Stack} \setminus \{ \epsilon \}) = \text{false} \\ &\text{top}(\text{push}(\text{Stack}, \text{Element})) = \text{Element} \\ &\text{pop}(\text{push}(\text{Stack}, \text{Element})) = \text{Stack} \} \\ \end{align*} $$